VISA: Variational Inference with Sequential Sample-Average Approximations

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel method for approximate inference in computationally intensive models, which is a significant challenge in many areas of machine learning and statistics. The proposed method, VISA, can substantially improve computational efficiency and offers a new approach to tackling high-dimensional inference problems.

Visual Insights

#

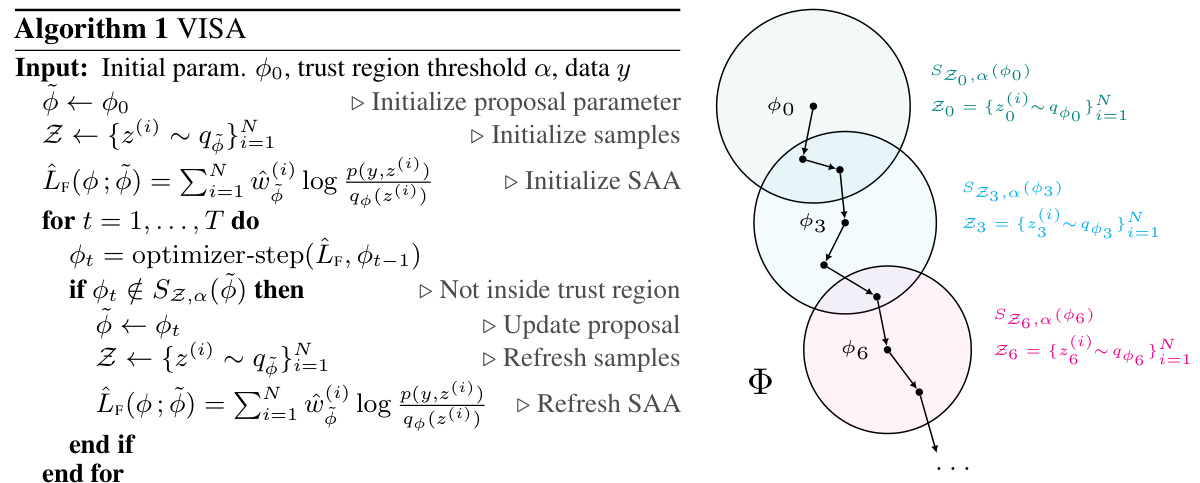
This figure visualizes how the VISA algorithm iteratively updates the variational parameters (φ) and constructs sequential sample average approximations (SAAs). Each circle represents an SAA, defined by a set of samples and a trust region (Sz,α(φ)). The algorithm starts with an initial proposal (φ0). As the optimizer updates the parameters, it checks if the updated parameters lie within the current trust region. If not, a new SAA is constructed with a new set of samples drawn from the updated proposal, defining a new trust region. This process repeats until convergence.

In-depth insights

#

VISA: Inference Engine

#

VISA, as a hypothetical inference engine, presents a novel approach to tackling computationally intensive models by leveraging sequential sample-average approximations (SAA). Its core strength lies in reusing model evaluations across multiple gradient steps, significantly reducing computational costs compared to traditional methods. This is achieved by constructing a series of SAAs, deemed valid within a trust region, thus creating a deterministic surrogate for the objective function. The trust region’s boundaries are dynamically adjusted based on an effective sample size measure, ensuring that the SAA remains an accurate representation of the posterior. VISA’s design makes it particularly suitable for models involving numerical simulations where gradient computations are difficult or impossible, offering a promising solution for inference in complex, high-dimensional systems. While promising, potential limitations may include bias introduced by SAA approximations, particularly at low effective sample sizes and the performance dependency on the conservatively chosen learning rates. Further research is needed to refine the trust region dynamics and explore alternative sample-average strategies for robust and accurate inference across various application domains.

SAA Efficiency Gains

#

The core idea behind achieving SAA efficiency gains lies in reusing model evaluations across multiple gradient steps. Standard variational inference methods often recalculate model evaluations for every gradient update, leading to significant computational overhead, especially for complex models. By employing sample-average approximations (SAAs), where a fixed set of samples is used to approximate the objective function within a defined trust region, the algorithm avoids redundant computations. The trust region concept is crucial, ensuring the SAA remains valid and accurate; once the optimization steps move outside this region, a new set of samples is generated. This clever strategy significantly reduces the number of expensive model evaluations required for convergence, hence leading to the efficiency gains. The tradeoff lies in potential bias introduced by the SAA. However, the paper shows that with a careful selection of parameters, like a conservative learning rate and trust region threshold, this bias is kept in check, allowing for significant speed-ups in convergence without compromising accuracy excessively. Conservative parameter choices seem key to effectively balance speed and accuracy within the framework of this approach.

Trust Region Control

#

Trust region control methods are crucial for balancing exploration and exploitation in optimization algorithms. They aim to ensure that updates to parameters remain within a safe, well-behaved region around the current solution. This prevents drastic changes that could lead to instability or divergence from a good solution, especially when dealing with complex or non-convex problems. In the context of variational inference, this is particularly useful for mitigating the high variance of gradient estimates, which commonly occurs when using stochastic methods. By restricting updates within a trust region, based on metrics such as effective sample size (ESS), one can make the optimization process more stable and efficient. A well-defined trust region dynamically adapts to the optimization landscape, shrinking or expanding as needed, enabling the algorithm to progress steadily toward optimal solutions while minimizing the risk of premature convergence to local optima. The effectiveness of a trust region is intimately linked to the choice of a suitable trust region metric and the threshold for triggering a region update. Poor choices here can lead to over-conservative or inefficient updates.

High-D Gaussian Tests

#

High-dimensional Gaussian tests are crucial for evaluating the performance of variational inference methods, especially in the context of simulation-based models where gradients are unavailable or computationally expensive. These tests offer a controlled environment to assess algorithm convergence and accuracy, providing valuable insights into the efficiency and robustness of different approaches. The use of high-dimensional Gaussians allows researchers to isolate the impact of dimensionality on the performance of variational inference algorithms, separating the effects of model complexity from other factors. The ability to exactly compute the KL divergence makes high-dimensional Gaussian tests particularly valuable for evaluating the approximation quality achieved by methods like VISA. By comparing VISA’s performance to established baselines like IWFVI and BBVI, under various learning rates and sample sizes, researchers can ascertain the effectiveness of VISA’s sequential sample-average approximation strategy. These tests illuminate VISA’s ability to achieve comparable accuracy with substantially fewer samples, especially when employing conservatively chosen learning rates, highlighting its computational efficiency. However, the results might also reveal limitations, such as sensitivity to learning rate and bias compared to IWFVI at low sample sizes. This nuanced analysis is vital for understanding VISA’s strengths and weaknesses and its suitability for various applications. The high-dimensional Gaussian tests form a cornerstone of the paper’s empirical validation, underscoring the importance of rigorous testing in developing and evaluating new approximate inference methods.

Future Work: Scaling

#

Future work on scaling variational inference with sequential sample-average approximations (VISA) could explore several promising avenues. Improving the efficiency of sample generation is crucial, perhaps through adaptive sampling strategies that focus computational resources on the most informative samples. Developing more sophisticated trust-region mechanisms is key; methods that dynamically adjust the trust region based on the model’s complexity and the optimization progress would enhance performance. Investigating the use of second-order optimization techniques within VISA’s framework could lead to faster convergence, particularly for high-dimensional models. Finally, a thorough theoretical analysis of VISA’s convergence properties, including under various conditions and different optimization techniques, would be valuable. Such work could guide the development of more robust and efficient scaling strategies for complex models.

More visual insights

#

More on figures

This figure compares the convergence speed of VISA and other variational inference methods (IWFVI, BBVI-SF, BBVI-RP) on Gaussian target distributions with diagonal and dense covariance matrices. It shows how the symmetric KL-divergence decreases over the number of model evaluations for different learning rates and VISA’s trust region threshold parameters (α). The results illustrate that VISA significantly outperforms IWFVI and BBVI-SF for smaller learning rates by reusing samples, but can become unstable with higher learning rates.

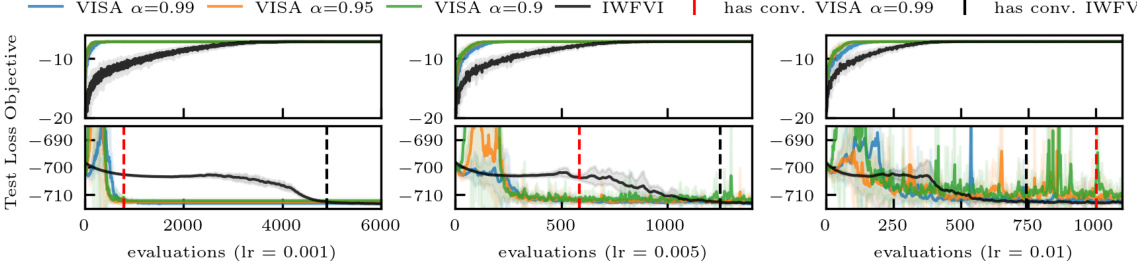
This figure shows the results of applying VISA and IWFVI to the Lotka-Volterra model with different learning rates. The top row displays the training objective as a function of the number of model evaluations, while the bottom row shows the approximate forward KL-divergence. The results demonstrate that VISA converges faster and achieves comparable accuracy to IWFVI for smaller learning rates, but requires more evaluations for larger learning rates unless a high effective sample size (ESS) threshold is used.

This figure presents the results of applying VISA and IWFVI to the Pickover attractor model. Panel (a) shows the log-joint density approximation improving over the number of model evaluations for VISA and IWFVI. Panel (b) displays the learned variational approximation of the log-joint density in the parameter space. Panels (c) and (d) visualize the resulting Pickover attractor for the ground truth parameters and the average parameters from the variational approximation respectively.

This figure compares the convergence speed of VISA against other methods (IWFVI, BBVI-SF, BBVI-RP) for approximating Gaussian distributions with diagonal and dense covariance matrices. The x-axis represents the number of model evaluations, and the y-axis shows the symmetric KL-divergence, measuring the difference between the approximate and true distributions. The results demonstrate VISA’s faster convergence, especially at lower learning rates, due to its sample reuse strategy. However, at higher learning rates, VISA’s stability decreases compared to IWFVI.

Full paper

#