↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning applications deal with data that inherently exists on non-Euclidean manifolds, like rotation matrices or covariance matrices. Existing methods for classifying such data are limited as they rely on specific geometric properties, hindering broad applicability. This often leads to performance issues or limited use in various domains.
This paper introduces a new framework, RMLR, that successfully extends multinomial logistic regression to handle general geometries. This is achieved by focusing on the Riemannian logarithm, a fundamental geometric operation. RMLR shows significant improvements over previous methods and is validated through various experiments on SPD manifolds and rotation matrices, demonstrating its effectiveness and broader applicability.
Key Takeaways#
Why does it matter?#
This paper is crucial because it extends multinomial logistic regression to various geometries, a significant step forward in machine learning. It addresses the limitations of existing approaches by proposing a framework applicable to a broader range of geometries. This opens new avenues for developing classifiers for manifold-valued data used in various applications, like computer vision and signal processing. It offers solutions to long-standing challenges in Riemannian geometry for machine learning, paving the way for improved efficiency and generalizability.
Visual Insights#

This figure illustrates the relationships between different Riemannian metrics defined on Symmetric Positive Definite (SPD) manifolds. The left panel shows how various metrics, including the Inverse Euclidean Metric (IEM), Square Root Euclidean Metric (SREM), and Polar Affine Metric (PAM), are related through power deformations. The right panel presents a Venn diagram visualizing the overlaps and distinctions among these metrics, highlighting the inclusion of certain metrics within broader families.
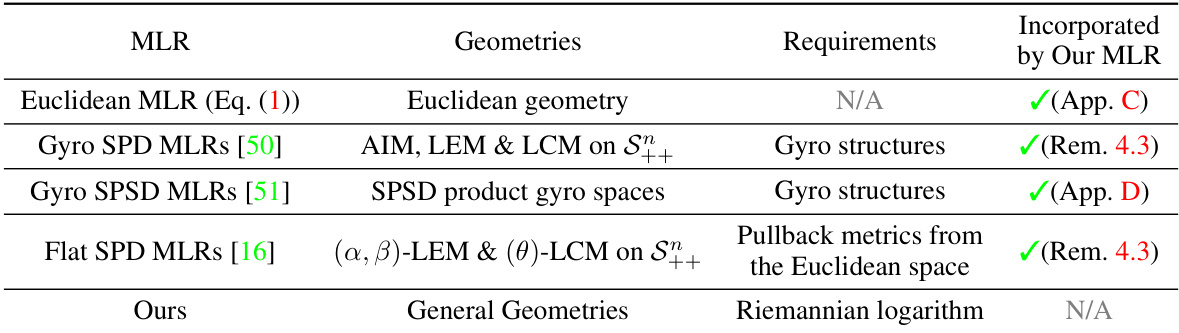
This table compares several existing Multinomial Logistic Regression (MLR) methods with the proposed Riemannian MLR (RMLR) in the paper. It shows that various existing MLRs designed for specific geometries (Euclidean, hyperbolic, SPD, SPSD manifolds) can be seen as special cases of the more general RMLR framework. The table highlights the geometries each method operates on, the specific Riemannian properties or requirements each method relies on, and whether the method is incorporated within the RMLR framework.
In-depth insights#
RMLR Framework#
The RMLR framework offers a flexible and broadly applicable method for extending multinomial logistic regression to Riemannian manifolds. Its strength lies in the minimal geometric requirements, needing only the Riemannian logarithm, making it suitable for various geometries. This contrasts with previous approaches which rely on specific manifold properties. The framework’s adaptability is showcased through applications to SPD manifolds and SO(n), demonstrating its versatility and potential for use with many other manifolds. A key benefit is the incorporation of several previous Riemannian MLRs as special cases, consolidating existing knowledge. The framework’s effectiveness is validated through experiments, highlighting consistent performance gains and enabling the exploration of geometries previously not considered. This generalized approach greatly advances the field of Riemannian deep learning.
SPD-MLR Metrics#
The effectiveness of Riemannian Multinomial Logistic Regression (RMLR) hinges significantly on the choice of Riemannian metric for the underlying Symmetric Positive Definite (SPD) manifold. Selecting appropriate SPD-MLR metrics is crucial because different metrics impose distinct geometric structures, influencing the calculation of distances, geodesics, and ultimately, classification performance. The paper explores five families of SPD MLR metrics, each arising from a power deformation of fundamental metrics like the Affine Invariant Metric (AIM), Log-Euclidean Metric (LEM), and Bures-Wasserstein Metric (BWM). This systematic exploration is valuable because it reveals how metric choice impacts both the theoretical properties (e.g., bi-invariance, geodesic completeness) and empirical effectiveness of the resulting SPD-MLR classifiers. Power-deformed metrics offer flexibility, allowing for interpolating between existing metrics and potentially discovering new, more suitable metrics for specific applications. The empirical evaluation demonstrates the impact of these metric choices on real-world classification tasks, underscoring the importance of carefully selecting metrics for optimal RMLR performance.
Lie Group MLR#
The concept of “Lie Group MLR” introduces a novel approach to extending multinomial logistic regression (MLR) to the realm of Lie groups, which are smooth manifolds with a group structure. This signifies a move beyond Euclidean-based MLR, which is limited in handling data with non-Euclidean geometries. A key advantage of this approach is its potential for broader applicability, as Lie groups represent a wide class of manifolds commonly found in machine learning applications. The framework likely leverages Lie group theory to define a Riemannian metric on the Lie group, enabling the formulation of a distance-based classification model. This would involve carefully defining the notion of a hyperplane within the Lie group, crucial for the margin-based formulation that’s common in MLR. The effectiveness relies on the availability of closed-form expressions for essential geometric operations, such as the Riemannian logarithm and parallel transport, to efficiently compute the necessary quantities for classification. Key challenges might involve the computational cost and potential numerical instability associated with calculations on non-Euclidean manifolds. However, the use of Lie groups offers potential benefits in handling data representing rotational or other group-related information, where the Lie group structure captures the intrinsic properties more effectively than other spaces. Therefore, Lie Group MLR holds promise as a powerful tool for analyzing manifold-valued data in various applications.
Experiment Results#
The experiment results section of a research paper is crucial for demonstrating the validity and effectiveness of the proposed methods. A strong results section will present findings clearly, using appropriate visualizations such as tables and graphs. Statistical significance should be meticulously reported to support claims. The results should be discussed in relation to the paper’s goals and hypotheses, highlighting successes and acknowledging any limitations. A direct comparison with relevant baselines or state-of-the-art methods is essential to demonstrate improvement or novelty. Furthermore, a thoughtful analysis of the results is vital, examining trends and potential outliers, and exploring possible explanations for unexpected findings. Reproducibility is paramount, requiring comprehensive details on experimental setup and parameters, making it possible for other researchers to replicate the results independently. The overall presentation of results needs to be concise, logical, and easy to follow, ensuring that the findings are readily accessible and interpretable by the audience.
Future Works#
The authors mention exploring various avenues for future research. Extending the Riemannian Multinomial Logistic Regression (RMLR) framework to handle a broader range of geometries is a key direction, as is addressing the over-parameterization issue in the current model, particularly as the number of classes increases. Another important area for future work is developing more efficient computational methods, especially for the complex Riemannian metrics, such as the power-deformed Bures-Wasserstein metric. The authors also plan to investigate the impact of different parallel transportation and Lie group translation methods on the accuracy and stability of RMLR and will explore the efficacy of their framework on more datasets and complex network architectures. Finally, in-depth theoretical analysis to further understand the underlying geometric properties that govern the success of RMLR across different manifolds will also be pursued. This holistic approach combines theoretical extensions with practical improvements to refine and broaden the applicability of the presented work.
More visual insights#
More on figures

This figure provides a visualization of SPD hyperplanes, which are submanifolds within the SPD manifold, generated using five different families of Riemannian metrics. Each subfigure represents a hyperplane derived from a specific metric, showcasing their distinct geometric properties and shapes within the 3D embedding space. The black dots highlight the boundary of the positive semidefinite cone, further illustrating the context and constraints of these hyperplanes within the SPD manifold.
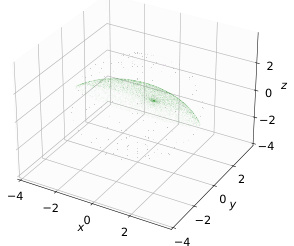
This figure provides a conceptual illustration of how different Riemannian metrics on SPD manifolds affect the shape of hyperplanes. Five families of Riemannian metrics ((θ, α, β)-LEM, (θ, α, β)-AIM, (θ, α, β)-EM, 2θ-BWM, θ-LCM) are visualized, each resulting in a unique hyperplane shape within the positive definite cone (S²⁺). The black dots represent the boundary of the positive definite cone. The visualization helps understand how the choice of metric impacts the decision boundary in the context of SPD multinomial logistic regression.
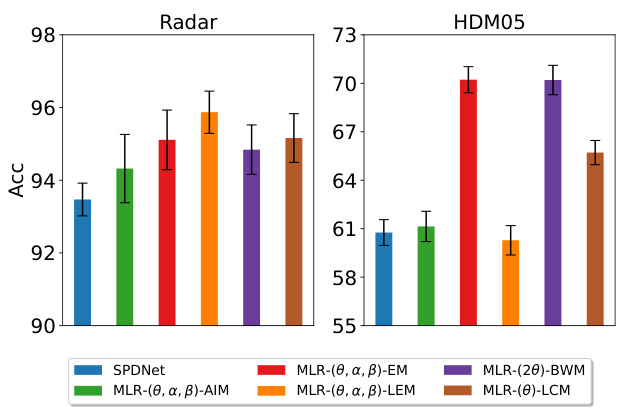
This figure visualizes the performance of SPDNet with various SPD MLRs (Multinomial Logistic Regressions) on two datasets, Radar and HDM05. The bar chart shows the average 10-fold cross-validation accuracy for each model, with error bars representing the standard deviation. The models compared include the baseline SPDNet without the MLR modification and five variations of the SPD MLR based on different Riemannian metrics. The figure illustrates the impact of the choice of Riemannian metric on the overall accuracy of the model.
More on tables
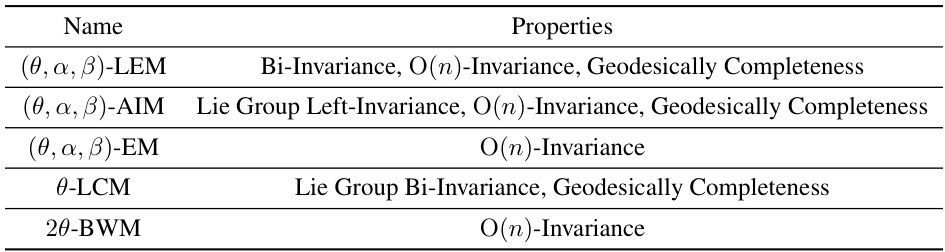
This table lists five Riemannian metrics on SPD manifolds and their properties. The metrics are (θ, α, β)-LEM, (θ, α, β)-AIM, (θ, α, β)-EM, θ-LCM, and 2θ-BWM. The properties shown are whether the metric is bi-invariant, left-invariant, O(n)-invariant and geodesically complete. These properties are important for understanding the geometric characteristics of the metrics and their suitability for use in Riemannian Multinomial Logistic Regression (RMLR).

This table presents a comparison of the performance of SPDNet (a type of neural network) with two different classifiers: LogEig MLR (a non-intrinsic classifier) and five different SPD MLRs (intrinsic classifiers based on different Riemannian metrics) on the Radar dataset. The table shows the balanced accuracy of the different methods with two different architectures of the network (2-block and 5-block). The results demonstrate that the proposed SPD MLRs consistently outperform the LogEig MLR, with varying performance gains depending on the specific Riemannian metric used. The table includes mean and standard deviation values for the results.

This table presents the results of experiments comparing the performance of SPDNet (a Riemannian neural network) using LogEig (a baseline Euclidean classifier) and several SPD MLRs (Riemannian multinomial logistic regressions) on the HDM05 dataset for human action recognition. Different architectures of SPDNet (1-Block, 2-Block, 3-Block) are evaluated. The table shows the balanced accuracy achieved by each method. The SPD MLRs use various metrics such as (θ, α, β)-EM, (α, β)-LEM, and 20-BWM. The goal is to demonstrate the performance improvement of the SPD MLRs over the LogEig classifier for human action recognition tasks.

This table presents the results of inter-session experiments using TSMNet with various Multinomial Logistic Regression (MLR) methods on the Hinss2021 dataset. It compares the balanced accuracy achieved by the LogEig MLR (baseline) against different SPD MLRs, each using a different Riemannian metric (AIM, EM, LEM, BWM, LCM) and various hyperparameters (θ, α, β). The table shows how different Riemannian metrics and hyperparameters affect the performance of the model.

This table presents the results of inter-subject experiments using TSMNet with various multinomial logistic regression (MLR) methods on the Hinss2021 dataset. It compares the balanced accuracy achieved by the LogEig MLR (a baseline non-intrinsic classifier) against the performance of several Riemannian MLRs using different metrics (AIM, EM, LEM, BWM, and LCM) and their power-deformed variants with varying hyperparameters. The table allows for the comparison of the effectiveness of different Riemannian metrics and their power deformations in the context of inter-subject EEG classification for mental workload estimation.

This table presents a comparison of the performance of LogEig MLR (a baseline Euclidean method) against SPD MLRs (Riemannian methods using different metrics on SPD manifolds) for action recognition. The experiments were conducted using the RResNet architecture on two datasets, HDM05 and NTU60. The table shows the balanced accuracy for each method with the improvement percentage over the LogEig MLR indicated in parentheses. The results demonstrate the improved performance of SPD MLRs, with some metrics showing significant gains over LogEig. Note that the best performance is shown in bold font.
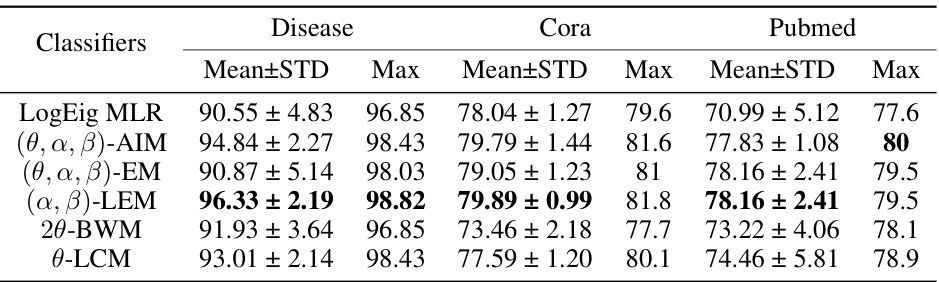
This table compares the performance of LogEig MLR (a baseline Euclidean classifier) against five different SPD MLRs (Riemannian classifiers based on various metrics) on three graph datasets: Disease, Cora, and Pubmed. The results are presented as mean ± standard deviation and maximum accuracy across multiple runs, showcasing the performance gains of the proposed Riemannian methods over the Euclidean approach.
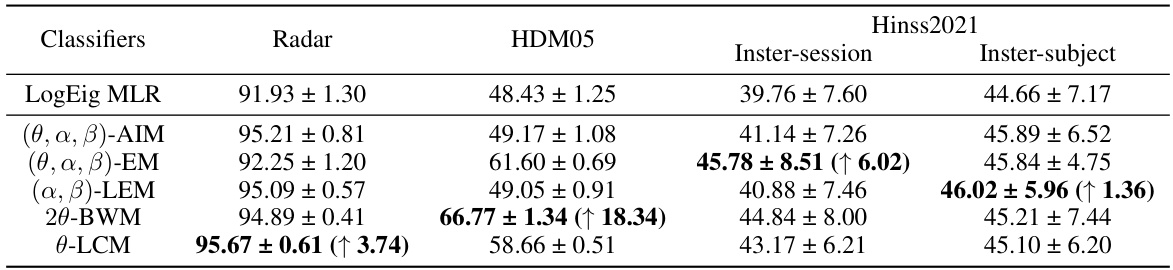
This table compares the performance of LogEig MLR (a baseline Euclidean classifier) against SPD MLRs (Riemannian classifiers on SPD manifolds) for direct classification on three datasets: Radar, HDM05, and Hinss2021. The results showcase the improvements achieved by the SPD MLRs, particularly highlighting the significant gains on the HDM05 dataset. The table also shows the improvement achieved by using the best hyperparameters (θ, α, β) for each SPD MLR.
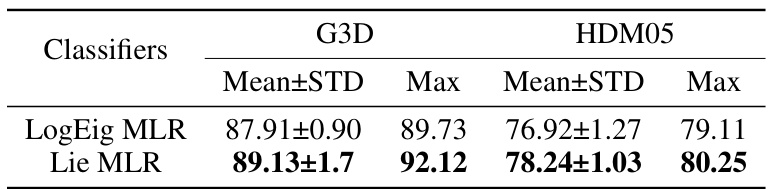
This table presents a comparison of the performance of LogEig MLR (matrix logarithm + FC + softmax) and Lie MLR on two datasets (G3D and HDM05). The LieNet architecture is used as the backbone network. The table shows that the proposed Lie MLR consistently outperforms the LogEig MLR on both datasets, demonstrating the effectiveness of the proposed method.

This table summarizes existing multinomial logistic regression (MLR) methods in different geometries and shows that they are special cases of the proposed Riemannian MLR (RMLR). It compares Euclidean MLR, gyro SPD MLRs, gyro SPSD MLRs, and flat SPD MLRs with the proposed RMLR, highlighting the geometries each applies to and the specific Riemannian properties each requires (if any). The RMLR only needs the Riemannian logarithm, demonstrating its broader applicability.

This table summarizes the relationship between several existing multinomial logistic regression (MLR) methods and the proposed Riemannian MLR (RMLR) framework. It shows that Euclidean MLR, gyro SPD MLRs, gyro SPSD MLRs, and flat SPD MLRs are all special cases of the more general RMLR framework. The table highlights the broader applicability of the RMLR due to its minimal geometric requirements, only needing the Riemannian logarithm, in contrast to other methods that rely on specific geometric properties like gyro structures or flat metrics.

This table shows that several existing Riemannian multinomial logistic regression (RMLR) methods on different geometries (Euclidean, hyperbolic, SPD, SPSD manifolds) are special cases of the proposed RMLR framework in the paper. It highlights the generality of the proposed framework by showing how it incorporates previous methods, which often rely on specific geometric properties, making it applicable to a wider range of geometries. The table lists the existing MLRs and their respective geometries, requirements, and whether they are incorporated into the proposed framework.

This table shows the hyperparameters (θ, α, β) used for the five families of SPD multinomial logistic regressions (MLRs) on the SPD Graph Convolutional Network (SPDGCN) backbone. Different hyperparameter settings are used for different datasets (Disease, Cora, Pubmed) to optimize the performance of the corresponding SPD MLRs.

This table summarizes several existing Multinomial Logistic Regression (MLR) methods and shows how they relate to the proposed Riemannian MLR (RMLR) framework. It highlights that the RMLR framework generalizes existing methods by requiring only minimal geometric properties, thus expanding its applicability to a wider range of geometries. The table lists various MLRs, including Euclidean MLR, Gyro SPD MLRs, Gyro SPSD MLRs, and Flat SPD MLRs, along with the geometries they operate on and the specific requirements they impose. It shows that the RMLR unifies these methods by only requiring a Riemannian logarithm, making it more widely applicable than previous methods.
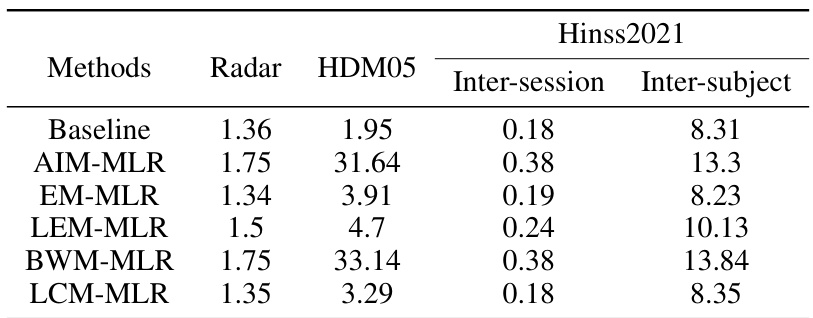
This table presents the training efficiency (seconds per epoch) for different SPD MLR methods on various datasets. The baseline represents the LogEig MLR, which is a non-intrinsic classifier, and the other methods represent intrinsic classifiers based on different Riemannian metrics. The datasets used are Radar, HDM05, and Hinss2021, and the metrics compared are AIM, EM, LEM, BWM, and LCM. The table shows that the intrinsic methods generally have higher training efficiency than the baseline on datasets with a small number of classes, but the performance difference decreases as the number of classes increases.
Full paper#