Quadratic Quantum Variational Monte Carlo

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in quantum chemistry and related fields due to its significant advancements in wavefunction optimization. Q2VMC offers a more efficient and accurate approach, potentially accelerating materials discovery and drug development. The novel discretized evolution method presented opens up new avenues for designing and improving variational quantum algorithms, sparking further research in this rapidly developing field.

Visual Insights

#

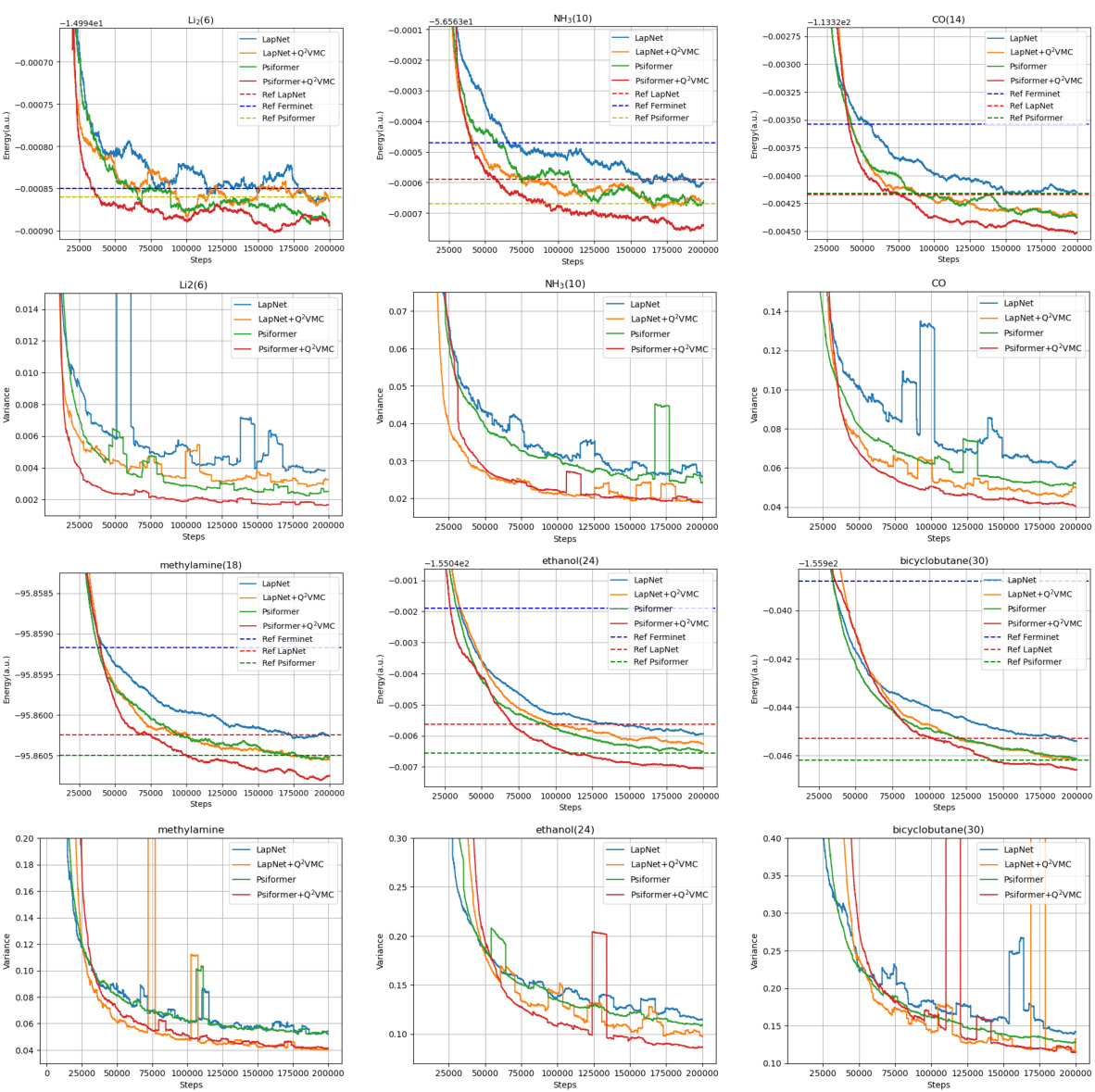
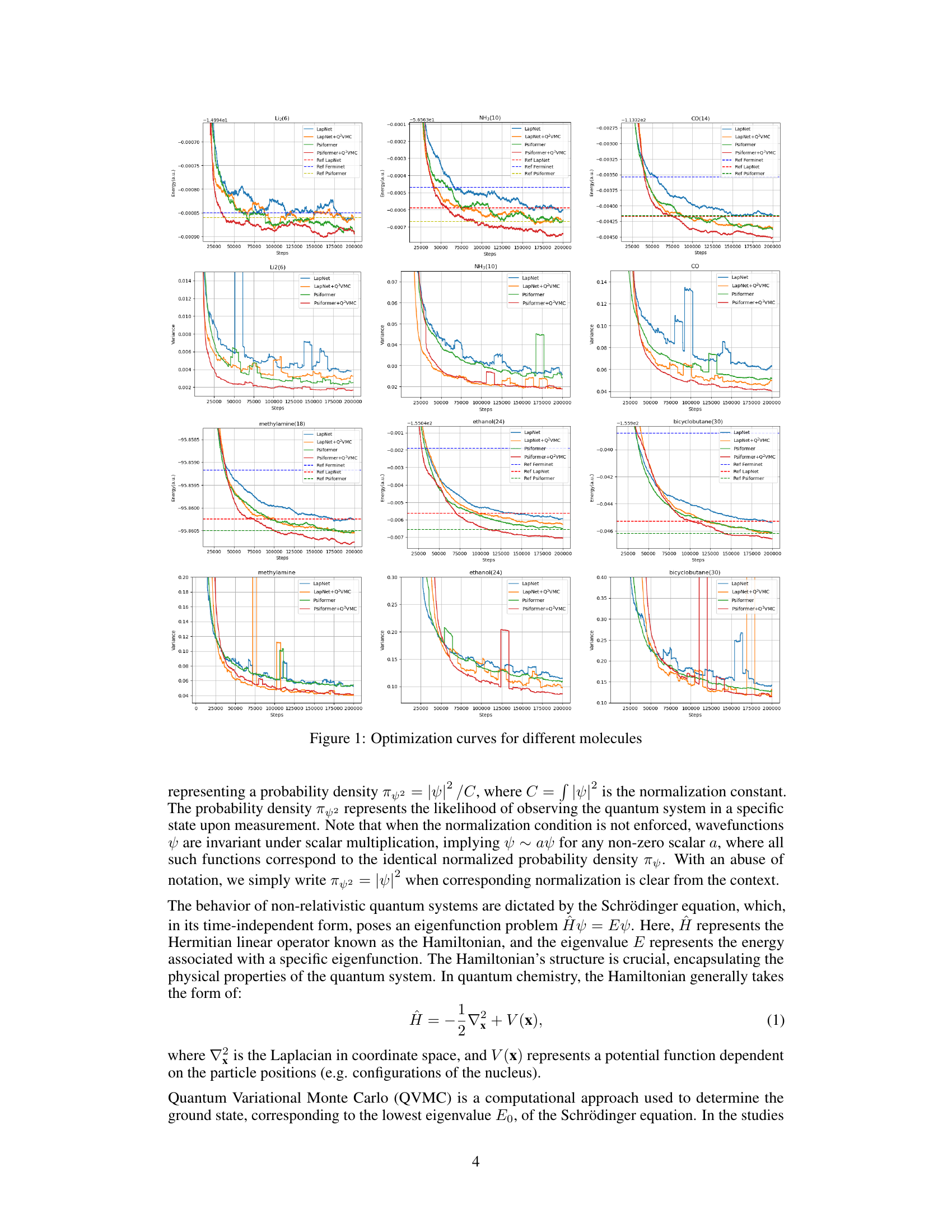
This figure shows the optimization curves for six different molecules (Li2, NH3, CO, CH3NH2, C2H6O, and C4H6). Each molecule is tested with two different neural network ansatzes (LapNet and Psiformer), with and without the Q2VMC optimization method. The graphs illustrate the energy and variance of the wave function over the training steps. The results show that Q2VMC converges faster and achieves lower energies for all tested molecules compared to conventional QVMC methods.

This table compares the ground state energies calculated using Psiformer and LapNet, with and without the Q2VMC optimization. The reference energies are taken from the original papers. The table demonstrates that Q2VMC generally leads to lower energies.

In-depth insights

#

Q2VMC Algorithm

#

The Q2VMC algorithm presents a novel approach to optimizing variational quantum Monte Carlo (QVMC) methods. Its core innovation lies in discretizing the imaginary-time Schrödinger equation, a continuous process traditionally approximated in QVMC. This discretization allows for finite-time steps, enhancing computational efficiency and stability. By projecting the discretely evolved probability distribution back into the parametric space of the neural ansatz using the Kullback-Leibler (KL) divergence, Q2VMC effectively navigates the challenges associated with non-convexity in the objective function. The algorithm integrates seamlessly with neural network-based ansatzes, offering a scalable and robust framework for wavefunction optimization in quantum chemistry. The inclusion of a quadratic term in the update mechanism, stemming from the inherent nature of probability distributions, further improves convergence speed and accuracy, as demonstrated by significant performance gains over standard QVMC methods across diverse molecular systems. The resulting enhanced accuracy and faster convergence, without additional computational cost, represent substantial advancements in the field of computational quantum chemistry.

Imaginary Time

#

The concept of “imaginary time” in the context of quantum mechanics and its application in quantum variational Monte Carlo (QVMC) methods is a powerful tool for achieving ground state estimations. It leverages the fact that imaginary-time evolution naturally guides the wavefunction toward the ground state, effectively transforming a challenging optimization problem into a more tractable evolution process. By discretizing this evolution, the method avoids the pitfalls of infinitesimal steps often required in continuous-time approaches, making it numerically stable and computationally efficient. This discretization allows for finite time steps while maintaining theoretical consistency with the continuous evolution process. The paper’s approach is particularly significant in the realm of variational quantum algorithms, offering a robust and scalable framework for future research in quantum chemistry and related fields. The use of imaginary time evolution in this method is key to its success as it avoids the non-convexity issues usually associated with direct ground state optimization.

KL Divergence

#

The Kullback-Leibler (KL) divergence is a pivotal concept in the paper, serving as the core measure for projecting the evolved wavefunction back into the parametric space of the neural network ansatz. The choice of KL divergence is not arbitrary; it leverages the inherent connection between wavefunctions and their probability distributions. Unlike other methods like quantum fidelity, KL divergence offers mathematical simplicity and effectively captures differences in probability distributions. The quadratic term naturally arising from the wavefunction’s squared nature in the probability distribution (|ψ|²) facilitates a computationally efficient approach. In essence, by minimizing KL divergence, the algorithm ensures the updated parametric wavefunction closely approximates the evolution within the Hilbert space, driving the optimization towards the ground state efficiently and accurately. This methodology cleverly sidesteps the complexities of other parametric projection methods, enhancing convergence speed and accuracy in the algorithm.

Future Directions

#

Future research should prioritize extending Q2VMC’s capabilities to larger molecular systems. Addressing the O(N4) scaling limitation is crucial for handling complex molecules relevant to materials science and drug discovery. Investigating the optimal imaginary time step and quantifying the projection errors inherent in the method would enhance its accuracy and robustness. Exploring applications beyond ground state calculations, such as excited state calculations and relative energy calculations, would significantly expand Q2VMC’s utility. Furthermore, comparing Q2VMC against other advanced methods for solving the Schrodinger equation, particularly on large-scale problems, could illuminate its advantages and limitations. Developing more efficient methods for computing the Fisher information matrix would accelerate convergence, making Q2VMC even more practical. Finally, theoretical analysis clarifying the relationship between the discretized imaginary time evolution and the parametric projection is needed to establish a more rigorous foundation for this promising algorithm.

Ablation Study

#

An ablation study systematically investigates the contribution of individual components within a machine learning model or algorithm to its overall performance. In the context of the Quadratic Quantum Variational Monte Carlo (Q2VMC) algorithm, an ablation study would likely focus on isolating the impact of the novel quadratic update mechanism. By comparing the performance of Q2VMC against a standard Quantum Variational Monte Carlo (QVMC) approach, while systematically removing or modifying different aspects of the Q2VMC update, researchers can determine which parts are crucial to its enhanced speed and accuracy. This may involve testing different learning rates to isolate the effect of the quadratic term. The ablation study’s findings are crucial for establishing the efficacy and value of each component of Q2VMC. It helps researchers understand how the different parts interact and which are most critical to its success. The results would strengthen the paper’s claims by confirming the essential role of the proposed quadratic update. By demonstrating a clear performance difference when parts of Q2VMC are removed, researchers can provide more compelling evidence that the proposed methodology is not simply an incremental improvement, but rather a significant advance in quantum computational chemistry.

More visual insights

#

More on figures

This figure displays the optimization curves for six different molecules (Li2, NH3, CO, CH3NH2, C2H6O, C4H6) using both the traditional QVMC method and the proposed Q2VMC method with two different neural network ansatzes (Psiformer and LapNet). The plots show the energy and variance as a function of the number of optimization steps. It demonstrates Q2VMC’s faster convergence and improved accuracy in achieving lower ground-state energies compared to the baseline QVMC approach.

This figure shows the optimization curves for six different molecules (Li2, NH3, CO, CH3NH2, C2H6O, C4H6) using both the traditional QVMC and the newly proposed Q2VMC methods. For each molecule, there are two curves, one for QVMC and one for Q2VMC, using two different neural network ansatzes (Psiformer and LapNet). The x-axis represents the number of steps in the optimization process, and the y-axis represents the energy variance. The figure illustrates the faster convergence of Q2VMC compared to QVMC across all molecules and ansatzes.

More on tables

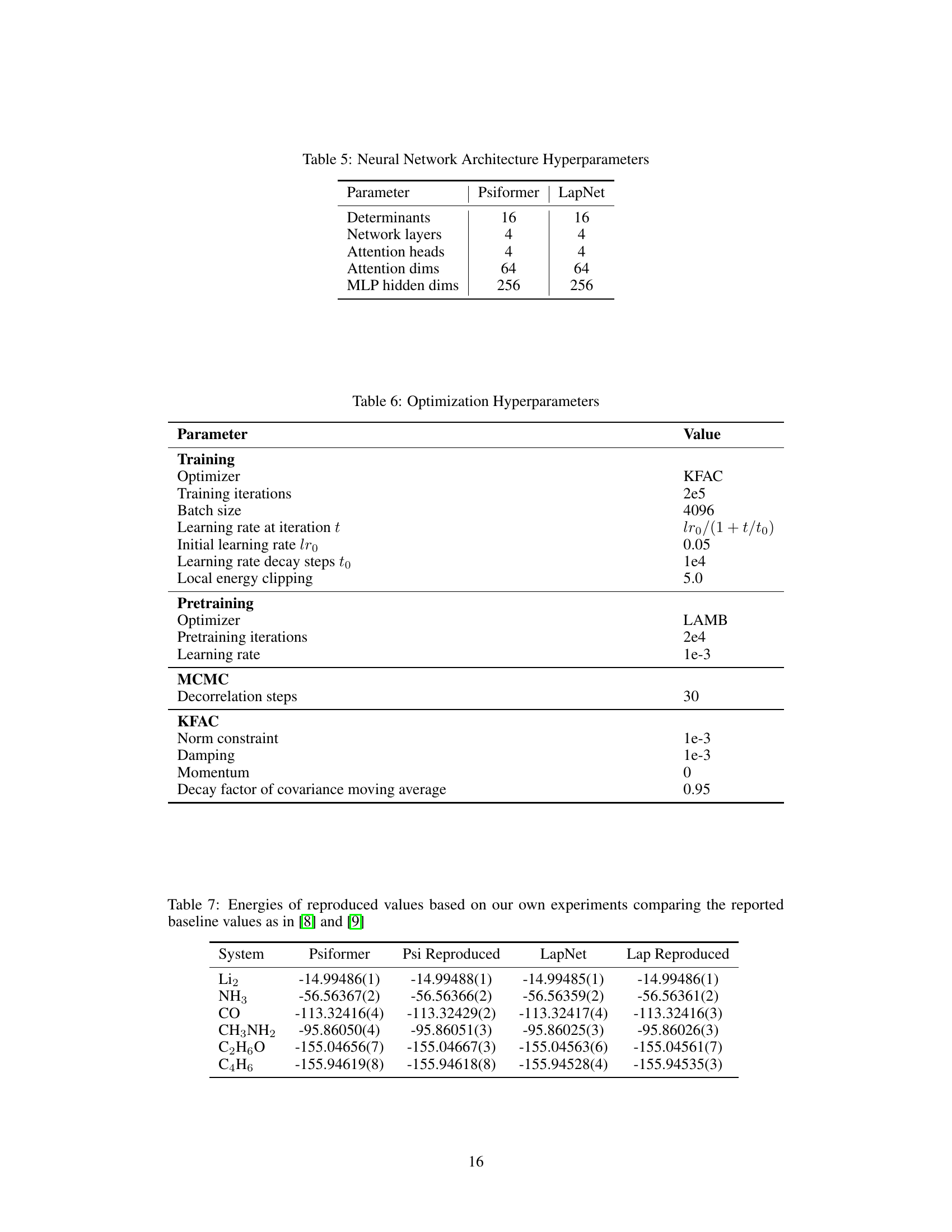
This table compares the ground state energies calculated by the Q2VMC method against those obtained using traditional QVMC methods (Psiformer and LapNet). It includes reference energies from the original papers for comparison. The goal is to demonstrate the improved accuracy of Q2VMC across various molecules of different sizes (number of electrons ranging from 6 to 30). The appendix contains additional baseline values to account for different evaluation strategies used in the original papers.

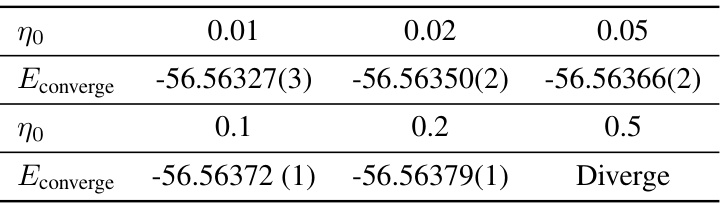
This table presents the convergence energies achieved for the NH3 molecule using the Q2VMC method with different learning rates (η0). It demonstrates the impact of varying the learning rate on the final energy achieved and shows that Q2VMC is robust even with different hyperparameter choices.

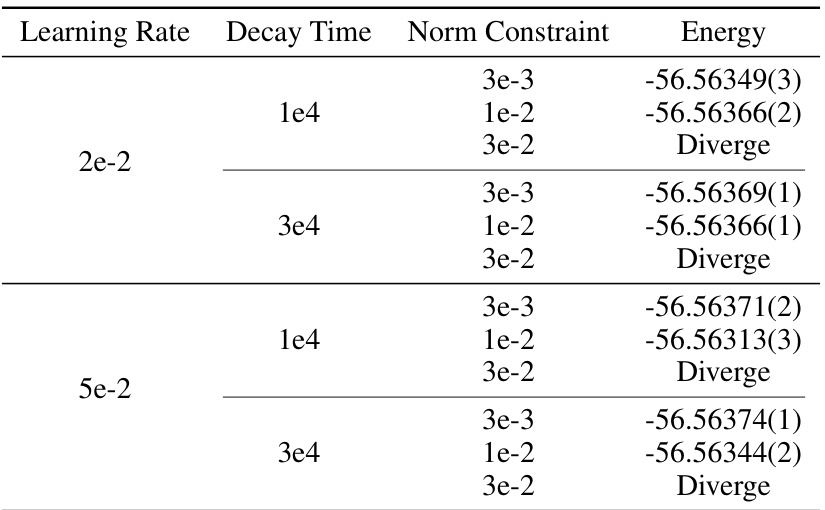
This table compares the ground state energies calculated by Psiformer and LapNet with and without the Q2VMC algorithm for six different molecules. The reference energies are taken from the original papers that introduced these neural network ansatzes. The purpose is to demonstrate the improved accuracy of Q2VMC compared to the original QVMC methods, even without hyperparameter tuning.

This table compares the ground state energies calculated using Psiformer and LapNet neural network ansatzes with the Q2VMC and QVMC methods. It shows that Q2VMC achieves lower ground state energies than QVMC across multiple molecular systems.

This table compares the ground state energies calculated by Q2VMC and the baseline methods (Psiformer and LapNet) for six different molecules. It demonstrates Q2VMC’s accuracy by showing that it achieves lower ground state energies than the baseline methods. The reference energies are also provided for comparison. The appendix contains additional results to account for differences in evaluation strategies.

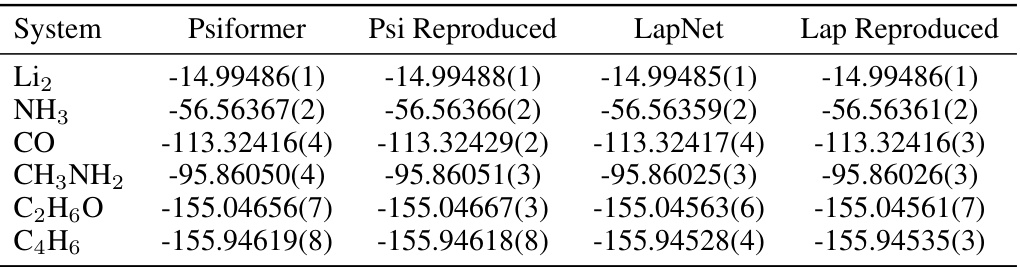
This table compares the ground state energies calculated using Psiformer and LapNet with and without the Q2VMC optimization for six different molecules. The reference energies are taken from the original publications, and the reproduced baselines show the accuracy of reproducing the results from those original papers. This table demonstrates the accuracy improvements achieved by Q2VMC across various molecules.

This table compares the energy values obtained using the Psiformer neural network with and without the Q2VMC optimization method. It also compares results from the original Psiformer paper ([8]), which used both a small and a large model, highlighting the improved accuracy achieved by Q2VMC using the smaller model.

Full paper

#