TL;DR#
Machine learning models often struggle in dynamic environments where data distributions shift unexpectedly. This affects model performance and makes it difficult to quantify the uncertainty of predictions. Prediction intervals, showing the range of likely outcomes, are crucial for addressing this challenge, but creating reliable intervals under distribution shifts remains an open problem. Existing methods focus on coverage guarantees but often fail to minimize interval width.
This research proposes a novel method to address this limitation. It combines different prediction interval methods to achieve a prediction interval with minimal width and strong coverage guarantees on the target domain, even without labeled target data. This approach is based on model aggregation techniques and has rigorous theoretical guarantees. Experiments on real datasets demonstrate its effectiveness compared to existing methods, showcasing improvements in both interval width and coverage.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on uncertainty quantification under distribution shifts, a prevalent challenge in machine learning. It offers a novel methodology for building reliable prediction intervals, particularly relevant in the context of unsupervised domain adaptation. The provided theoretical guarantees and practical applications make it valuable for enhancing the reliability and applicability of machine learning models in real-world scenarios.
Visual Insights#

🔼 This figure presents histograms visualizing the distribution of coverage and bandwidth obtained from 200 experimental runs using Algorithm 1 on the airfoil dataset. The top row displays the results for the proposed method, showcasing its coverage and bandwidth performance. The bottom row presents similar histograms for a weighted conformal prediction method, allowing a comparison of the two approaches in terms of both coverage and width of their prediction intervals.
read the caption
Figure 1: Experiments on Airfoil data using Algorithm 1

🔼 This table compares the performance of the proposed method and the Weighted Variance-adjusted Conformal (WVAC) method in terms of average width of prediction intervals across various maximum depths of a model. The median coverage is given in parentheses for each method and depth, illustrating that the proposed method maintains consistently smaller widths while achieving comparable coverage even as model complexity (depth) increases.
read the caption
Table 1: Robustness of our method and WVAC. The number inside the parenthesis is the median of coverage over these Monte Carlo iterations.
In-depth insights#
Interval Aggregation#
The concept of ‘Interval Aggregation’ in the context of prediction intervals under domain shift is crucial. It addresses the challenge of combining multiple prediction intervals, each potentially offering varying levels of accuracy and coverage, to produce a single, more reliable interval. The effectiveness of aggregation hinges on the relationships between source and target domains. If domains are similar (e.g., covariate shift), simpler aggregation methods might suffice. However, for more substantial shifts (e.g., measure-preserving transformation), more sophisticated techniques that account for domain discrepancies become necessary. The optimal aggregation method will depend on factors such as the computational cost, theoretical guarantees on coverage and width, and the specific characteristics of the prediction intervals being combined. A successful aggregation strategy should minimize interval width while maintaining sufficient coverage, leading to more precise and informative uncertainty quantification. The theoretical analysis supporting interval aggregation is critical for establishing the reliability and validity of the final prediction interval, ensuring it accurately reflects the uncertainty in the target domain.
Domain Shift Methods#
Domain shift, a crucial challenge in machine learning, arises when the distribution of test data differs from training data. This necessitates robust methods to mitigate performance degradation. Addressing domain shift often involves techniques that bridge the gap between source and target domains, leveraging labeled source data and potentially unlabeled target data. Common strategies include transfer learning, which adapts models trained on the source domain to the target; domain adaptation, which modifies the model or data to reduce domain discrepancy; and domain generalization, aiming for models that generalize well across diverse unseen domains. The choice of method depends heavily on the nature of the domain shift, whether it’s covariate shift (distribution of input features changes) or concept shift (relationship between input and output changes), and the availability of labeled target data. Effective approaches often incorporate techniques like domain adversarial training (to encourage domain-invariant features) or optimal transport (to align source and target distributions). Evaluating the success of a domain shift method requires careful consideration of metrics beyond simple accuracy, including measures of uncertainty and generalization performance across different target domains. Ultimately, robust solutions are those that balance model complexity and generalization capability while providing reliable performance in the presence of distributional shifts.
Theoretical Guarantees#
The theoretical guarantees section of a research paper on prediction intervals under unsupervised domain shift would rigorously justify the proposed methodology’s reliability. It would likely establish finite-sample bounds on the prediction interval’s width and coverage probability. This would involve demonstrating that the interval’s width remains relatively small while ensuring a high probability of containing the true value of the target variable. The theoretical analysis might consider different scenarios, such as covariate shift (where the input distributions differ but the conditional distribution remains the same) and domain shift (where the conditional distribution also changes), proving that the proposed method still delivers accurate prediction intervals under these more complex situations. Assumptions made about the data generating process, such as bounded density ratio or measure-preserving transformations between domains, would be clearly stated and their impact on the theoretical results discussed. Ultimately, this section should provide a convincing argument for the method’s practical applicability, showing not only its performance but also the mathematical reasoning that makes it successful.
Empirical Validation#
An Empirical Validation section in a research paper would ideally present a robust evaluation of the proposed methodology. This would involve applying the method to multiple real-world datasets, carefully selecting datasets to cover various scenarios and complexities. Quantitative results demonstrating the method’s performance on key metrics like prediction interval coverage and width would be crucial. The results should be compared to those of existing state-of-the-art methods, showcasing the advantages and limitations of the proposed approach. Statistical significance testing would add credibility to the claims made. Moreover, a discussion comparing the computational efficiency, memory usage, and time required of the new method with alternatives is important. A thorough analysis would also include visualizations to improve understanding of the results, such as histograms or boxplots for performance metrics across datasets. It should showcase the reliability and effectiveness across diverse scenarios. Finally, addressing potential limitations or challenges encountered during the empirical validation and suggesting directions for future work will make this section comprehensive.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the methodology to handle more complex forms of domain shift, beyond covariate shift and measure-preserving transformations, is crucial. This might involve scenarios with significant changes in conditional distributions or more intricate relationships between source and target domains. Developing more sophisticated methods for estimating the density ratio or optimal transport map is another key area, as the accuracy of these estimates directly impacts the performance of the proposed prediction intervals. Investigating alternative aggregation techniques, beyond the convex optimization framework used here, could potentially lead to more efficient or robust methods. Exploring the application of the proposed methodology to different types of prediction problems, such as regression, classification, or time series forecasting, is also warranted. Finally, a thorough empirical evaluation on a wider range of datasets is essential to further assess the method’s generalizability and practical applicability across diverse contexts and to investigate the sensitivity to different parameter choices and hyperparameter settings. Addressing these questions will further solidify the theoretical underpinnings and enhance the practical impact of the presented methodology.
More visual insights#
More on figures

🔼 This figure presents the histograms of the coverage and average bandwidth of the proposed method and the weighted conformal prediction method over 200 experiments. The results show that the proposed method consistently yields a shorter prediction interval than the weighted conformal prediction while maintaining adequate coverage. The figure also includes a table summarizing the average and median width for various maximum depths of the prediction interval in each method. These results demonstrate that the proposed method effectively balances coverage and width, especially as the model complexity (depth) increases.
read the caption
Figure 1: Experiments on Airfoil data using Algorithm 1
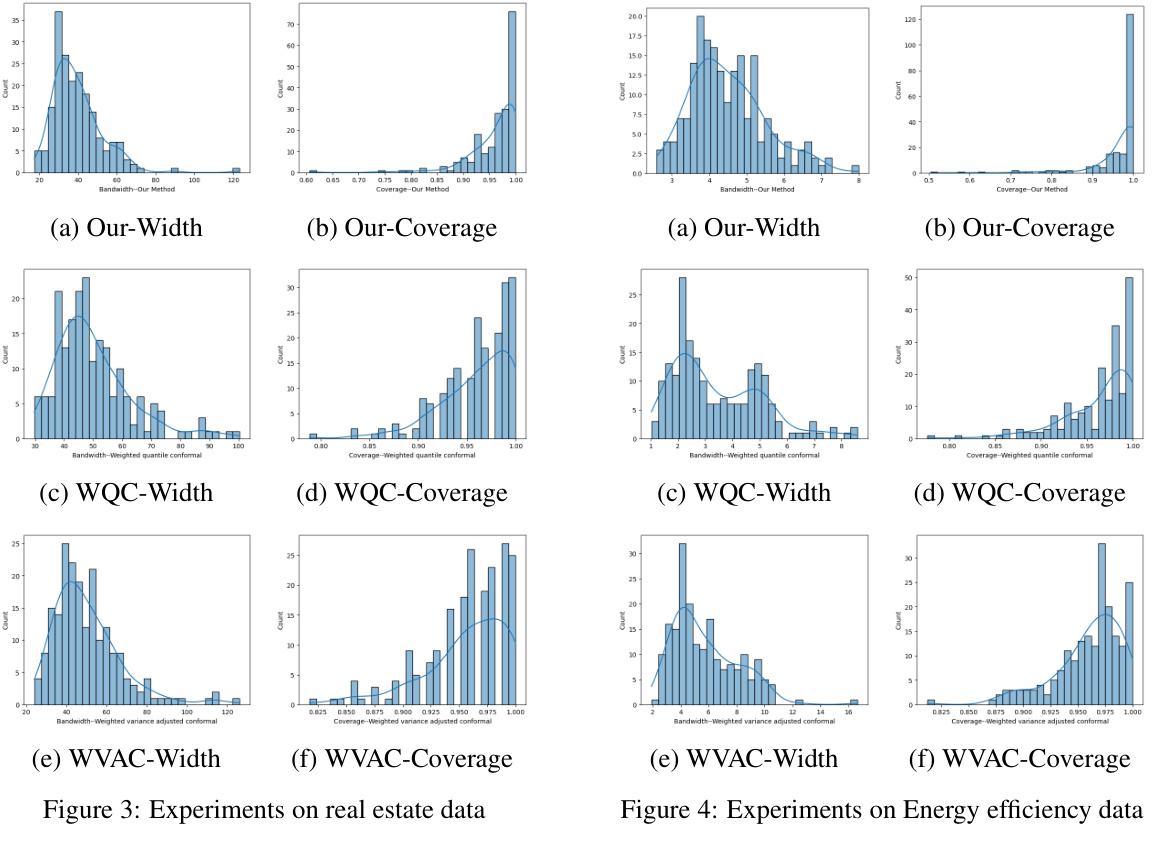
🔼 This figure shows the histograms of coverage and average bandwidth for three different methods: the proposed method, weighted quantile conformal, and weighted variance-adjusted conformal methods. The results are based on experiments with real estate data. The histograms show the distribution of coverage and bandwidth across multiple runs, allowing a comparison of the performance of the three methods.
read the caption
Figure 3: Experiments on real estate data
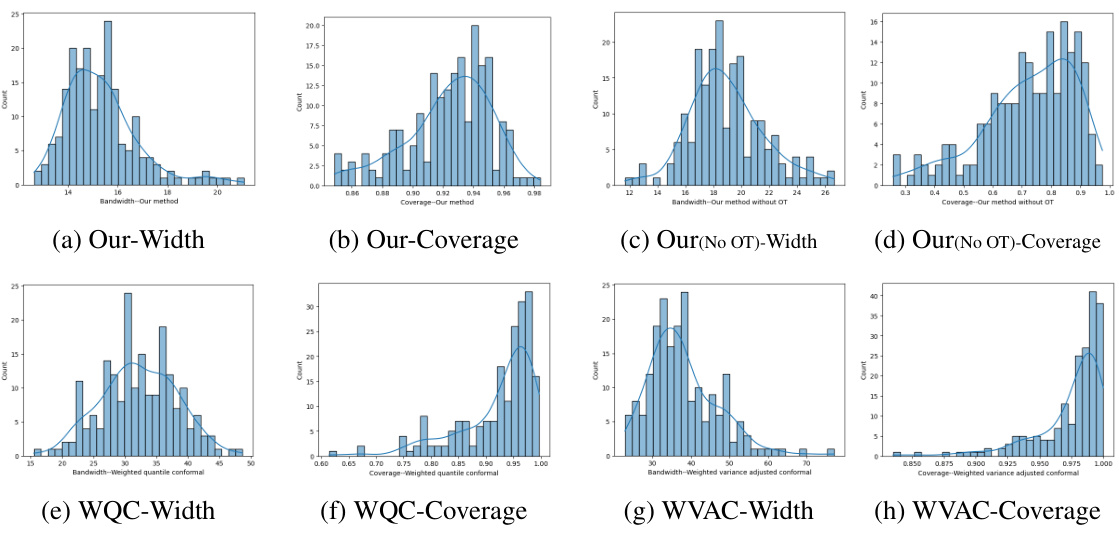
🔼 This figure shows the results of experiments conducted on the Airfoil dataset using optimal transport. The figure displays histograms of bandwidth and coverage for four different methods: the proposed method (with and without optimal transport), Weighted Quantile Conformal, and Weighted Variance-Adjusted Conformal. Each histogram visually compares the distribution of bandwidths and coverages produced by these different methods. This allows for a comparison of the methods’ performance in terms of both the precision and accuracy of their prediction intervals.
read the caption
Figure 5: Experiments on Airfoil data using optimal transport
More on tables
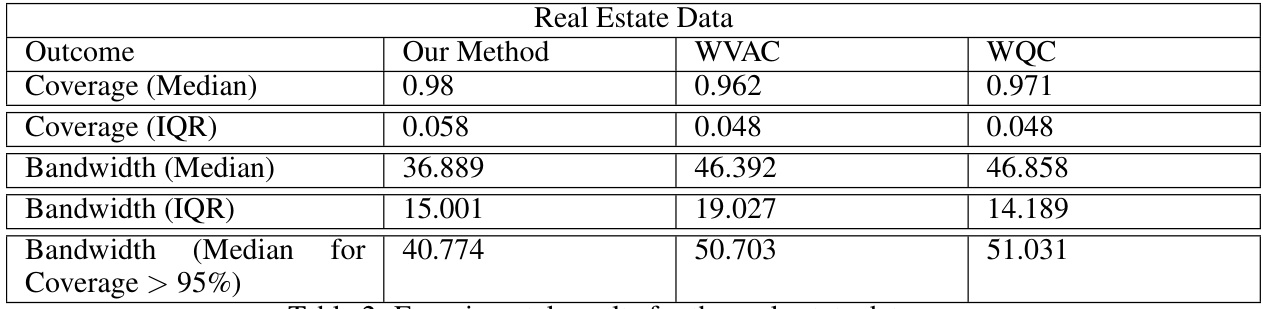
🔼 This table presents the experimental results for the real estate dataset. It compares the performance of three methods: the proposed method, the Weighted Variance-adjusted Conformal (WVAC) method, and the Weighted Quantile-adjusted Conformal (WQC) method. The metrics evaluated include median and interquartile range (IQR) of coverage and bandwidth, as well as the median bandwidth when requiring a coverage exceeding 95%. The results show the proposed method achieves comparable coverage to the other methods, but with a significantly smaller prediction interval width.
read the caption
Table 2: Experimental results for the real estate data

🔼 This table presents the median and interquartile range (IQR) of coverage and bandwidth for three different methods: the proposed method, Weighted Variance-adjusted Conformal (WVAC), and Weighted Quantile-adjusted Conformal (WQC) applied to energy efficiency data. The bandwidth is further broken down by median bandwidth for coverages exceeding 95%. The results are based on 200 Monte Carlo experiments.
read the caption
Table 3: Experimental results for the energy efficiency data

🔼 This table presents the experimental results for the Appliances Energy Prediction Dataset. The results compare the performance of three methods (Our Method, WVAC, WQC) in terms of coverage and bandwidth. The table shows that our method provides a narrower prediction interval while maintaining adequate coverage.
read the caption
Table 4: Experimental results for the Appliances Energy Prediction Dataset

🔼 This table presents the median coverage and bandwidth of prediction intervals obtained using three different methods (Our Method, WVAC, and WQC) on the ETDataset. The ETDataset is a time series dataset of hourly-level data from two electricity transformers. The results are based on 200 Monte Carlo simulations, where the data is split into source and target domains using geographical information. The table shows that Our Method outperforms the other methods in terms of bandwidth while maintaining a good coverage.
read the caption
Table 5: Experimental results for the ETDataset
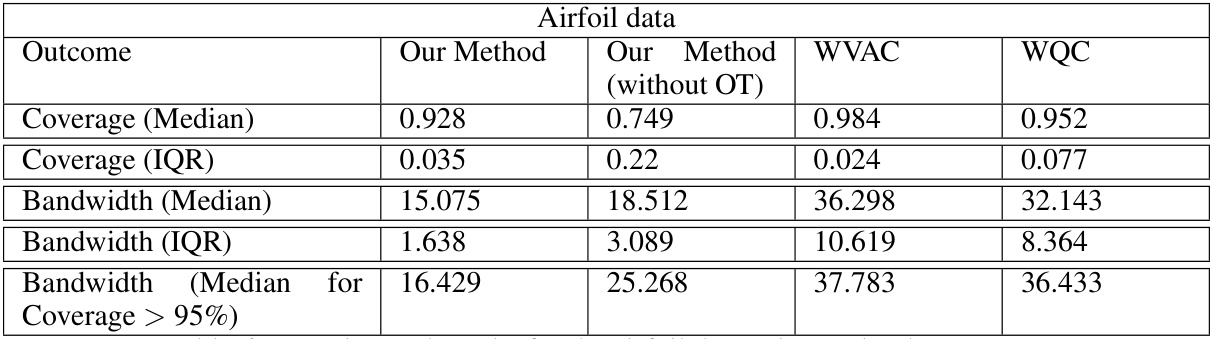
🔼 This table presents the experimental results for the airfoil dataset using optimal transport. It compares the performance of the proposed method (with and without optimal transport) against two other conformal prediction methods (WVAC and WQC) in terms of coverage and bandwidth of prediction intervals. The median and interquartile range (IQR) of coverage and bandwidth are shown, along with the median bandwidth for cases with coverage greater than 95%.
read the caption
Table 6: Experimental results for the airfoil data using optimal transport
Full paper#



















