↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Collaborative learning enhances AI models by combining information from multiple sources, but traditional approaches often require sharing sensitive private data and model parameters. This paper focuses on distillation-based collaborative learning (DCL), a promising alternative that leverages publicly available unlabeled data for model training without direct data or model exchange. However, existing DCL algorithms are unsatisfactory and lack theoretical backing.
This research rigorously analyzes a DCL algorithm (FedMD) using a non-parametric approach. They prove its near-minimax optimality for massively distributed heterogeneous data, a significant theoretical breakthrough. Inspired by these results, a practical DCL algorithm for neural networks (DCL-NN) is introduced, addressing heterogeneous architectures via feature kernel matching. Extensive experiments showcase DCL-NN’s improved performance over existing methods, demonstrating its value for practical application.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel theoretical understanding of distillation-based collaborative learning, a significant area in decentralized AI model training. It presents the first nearly minimax optimal algorithm that doesn’t require direct data or model sharing, addressing a major hurdle in collaborative learning. This work is relevant to current trends in federated learning and distributed AI, opening up new research avenues in algorithm design and theoretical analysis for collaborative learning in diverse, decentralized settings. The practical algorithm proposed also bridges the gap between theory and practice, providing a valuable tool for real-world applications.
Visual Insights#

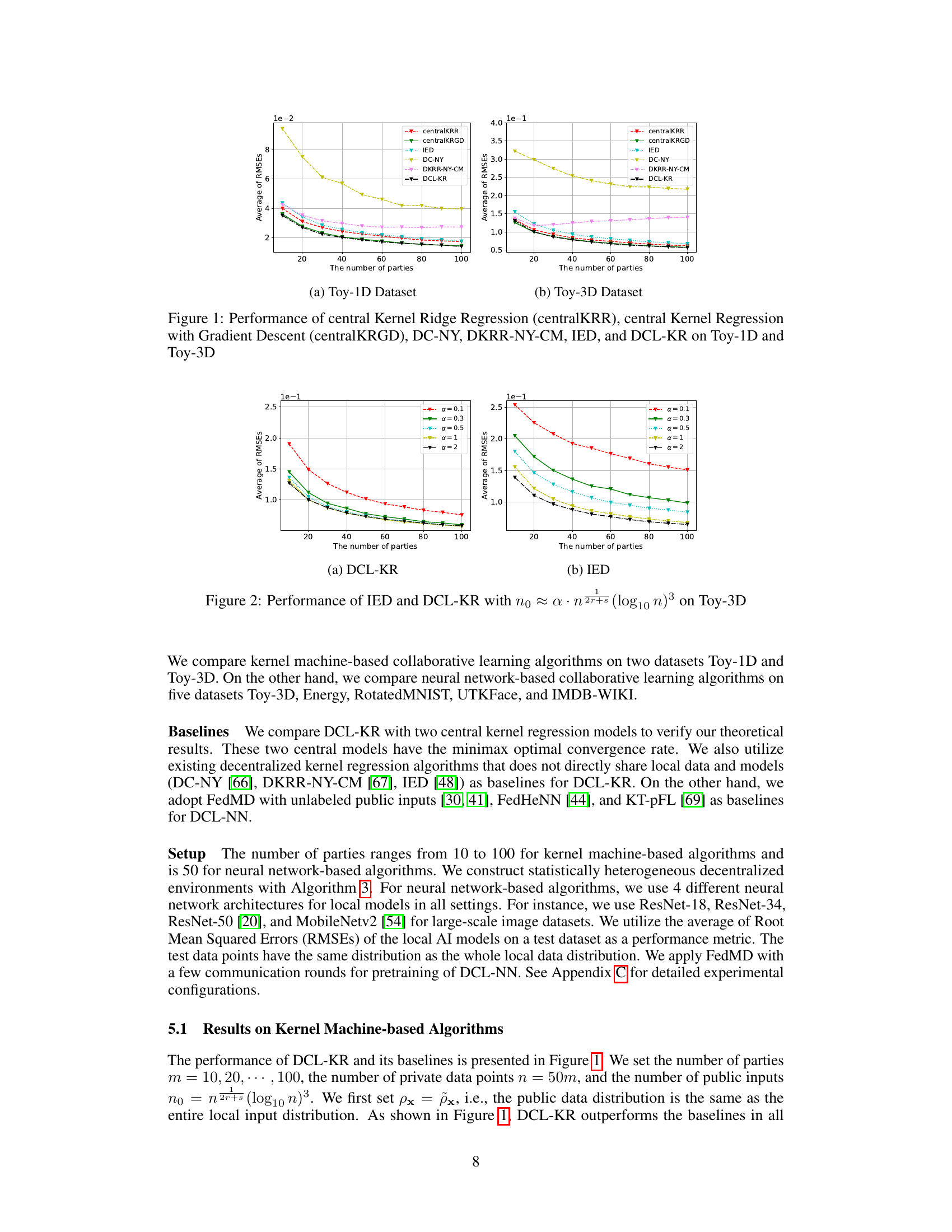
The figure compares the performance of six different algorithms on two toy datasets: Toy-1D and Toy-3D. The algorithms include two centralized kernel regression methods (centralKRR and centralKRGD), three decentralized kernel regression methods (DC-NY, DKRR-NY-CM, and IED), and the proposed distillation-based collaborative learning algorithm (DCL-KR). The y-axis represents the average RMSE, while the x-axis represents the number of parties. The figure shows that DCL-KR outperforms other algorithms in most cases. For both Toy-1D and Toy-3D, DCL-KR maintains the near-optimal convergence rate in terms of the number of parties.

This table compares several decentralized collaborative learning algorithms using kernel regression, focusing on their ability to achieve near minimax optimality while addressing challenges such as local data privacy, massive distribution, and non-i.i.d. (independent and identically distributed) data. It highlights whether each algorithm protects local data privacy, functions well in massively distributed settings, and handles non-i.i.d. data effectively. The table also notes that one algorithm, IED, achieves a weaker form of minimax optimality compared to the ideal.
In-depth insights#
DCL: A New Paradigm#
The concept of “DCL: A New Paradigm” suggests a significant shift in collaborative learning. It likely proposes distillation-based methods as a superior alternative to traditional approaches that require direct data or model sharing. This paradigm shift prioritizes privacy by focusing on sharing knowledge distilled from models trained on public datasets rather than raw private data. The core innovation likely lies in the theoretical framework that underpins DCL, potentially proving its effectiveness in diverse and challenging settings such as massively distributed and statistically heterogeneous environments. This theoretical backing is likely complemented by practical algorithm designs that demonstrate the feasibility and efficacy of the proposed method. A key aspect of this new paradigm might be its near-minimax optimality, ensuring efficiency even with many participants and non-identical data distributions. The heading implies that DCL is more than just an incremental improvement; it represents a fundamental change in how collaborative machine learning is approached.
Kernel Distillation#
The concept of ‘Kernel Distillation’ in the context of the provided research paper appears to involve a technique for aligning the feature spaces of heterogeneous neural networks to facilitate effective collaborative learning. The core idea is to bridge the gap between the theoretical advantages of kernel-based methods and the practical reality of using neural networks, which may have diverse architectures and feature representations. By focusing on kernel matching, rather than direct model parameter exchange, the method aims to preserve local model privacy while still enabling knowledge transfer. This involves distilling knowledge from local models onto a shared, ensemble kernel, effectively harmonizing the feature representations. This approach enhances the efficiency and effectiveness of the collaborative learning process by enabling minimax optimal convergence rates in diverse environments. The use of kernel alignment measures, such as CKA, is crucial for evaluating and guiding the kernel matching procedure, ensuring that the local feature kernels effectively align with the target ensemble kernel. Overall, this distillation technique is key to extending the theoretical benefits of kernel-based methods to practical collaborative learning settings with neural networks.
Heterogeneous NN#
In the context of a research paper focusing on collaborative learning, the concept of “Heterogeneous NN” likely refers to the use of neural networks with differing architectures or configurations across multiple participating agents or nodes. This heterogeneity presents significant challenges to the efficiency and accuracy of collaborative training, as standard approaches (like federated learning) often assume homogeneity. The core challenge is reconciling the diverse outputs and internal representations of these networks to reach a consensus model. A key research direction involves finding effective mechanisms for information exchange and aggregation that overcome architectural differences. This might include techniques such as knowledge distillation, where the knowledge encoded in heterogeneous networks is transferred using a shared, intermediary representation. The paper likely investigates methodologies to bridge this gap, potentially employing techniques like kernel matching or feature alignment to harmonize disparate network structures and facilitate effective collaboration. This involves comparing and contrasting the performance of different algorithms in heterogeneous environments, evaluating their effectiveness in terms of both accuracy and communication efficiency. Ultimately, the research will likely showcase how handling heterogeneity is crucial for building practical and scalable collaborative learning systems.
Convergence Analysis#
A convergence analysis in a machine learning context typically involves studying how a model’s parameters change over time during training and whether they approach a stable solution. Key aspects often considered include the rate of convergence, measuring how quickly the model improves, and whether the model converges to a global optimum or merely a local optimum. The analysis might involve theoretical bounds on the convergence rate under certain assumptions about the data and model, or it could involve empirical evaluation of convergence behavior on various datasets. Factors affecting convergence, such as learning rate, model architecture, and data characteristics, are usually examined. Furthermore, a robust analysis would delve into the relationship between the convergence behavior and the model’s generalization performance, ascertaining whether faster convergence translates to improved generalization on unseen data. Establishing these connections is crucial to understanding a model’s overall effectiveness and reliability.
Future of DCL#
The future of distillation-based collaborative learning (DCL) holds exciting possibilities. Addressing the limitations of current DCL methods is crucial; this includes improving robustness to heterogeneous data distributions and network architectures, and developing more efficient communication strategies. Theoretical advancements are needed to better understand the convergence rates and generalization capabilities of DCL in various settings, particularly in non-i.i.d. and massively distributed scenarios. Practical applications of DCL should be explored across diverse fields, such as federated learning, distributed machine learning, and multi-agent systems. Enhanced privacy-preserving mechanisms within DCL are essential to ensure wider adoption and trust, which may involve exploring techniques beyond simple model aggregation. Furthermore, research on combining DCL with other collaborative learning paradigms could lead to hybrid approaches with superior performance and robustness.
More visual insights#
More on figures

The figure shows the performance of the IED and DCL-KR algorithms on the Toy-3D dataset for varying numbers of parties (m) and different values of α. The number of public inputs (n0) is proportional to α * n^(2r+s) * (log10 n)^3. It illustrates that DCL-KR requires fewer public inputs (smaller α) to achieve high performance compared to IED, as predicted by the theoretical results.
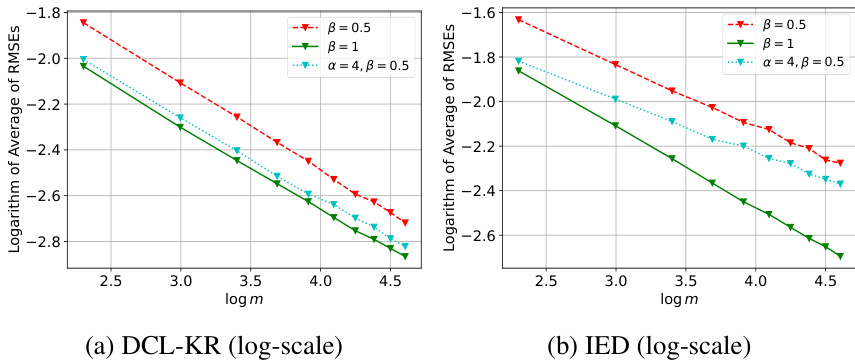
This figure compares the performance of IED and DCL-KR algorithms on the Toy-3D dataset when the public data distribution (px) is different from the local data distribution (px). The x-axis represents the logarithm of the number of parties (log m), and the y-axis represents the logarithm of the average of root mean squared errors (log RMSE). Different lines represent different settings of the parameters α and β, which control the relationship between px and px. The figure shows that DCL-KR maintains a consistent convergence rate even when px ≠ px, whereas IED’s performance is significantly affected by the change of px.
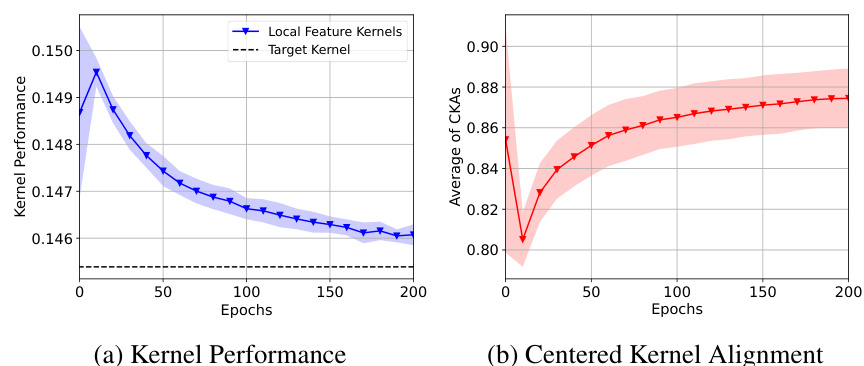
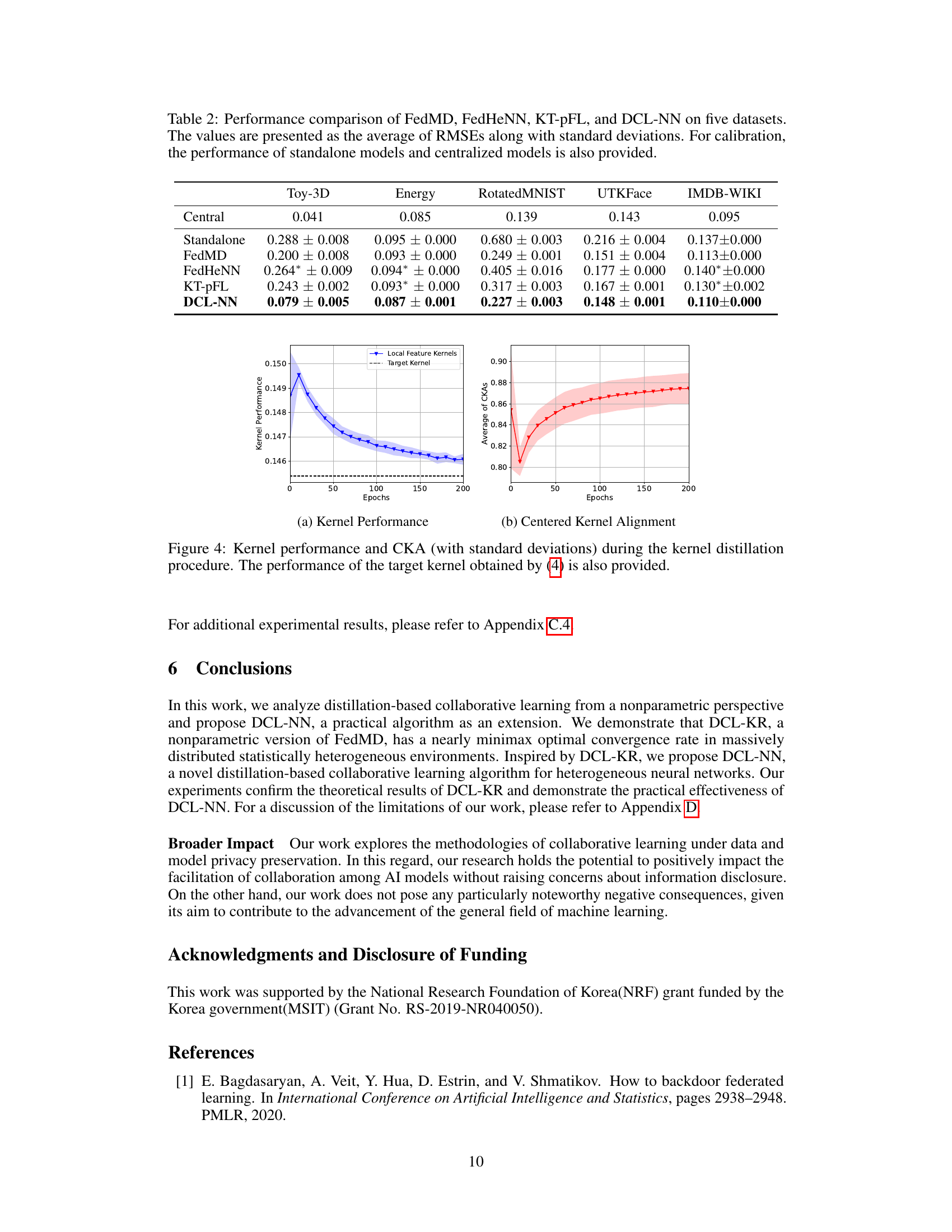
This figure shows the results of the kernel distillation procedure on the UTKFace dataset. The left panel displays the RMSE of a kernel linear regression model trained on all local data, showing the kernel performance improving after initial degradation. The right panel shows the average CKA between the local feature kernels and the target kernel, increasing over time towards higher alignment. The shaded region represents standard deviations, and the dotted line indicates the performance of the ensemble kernel.
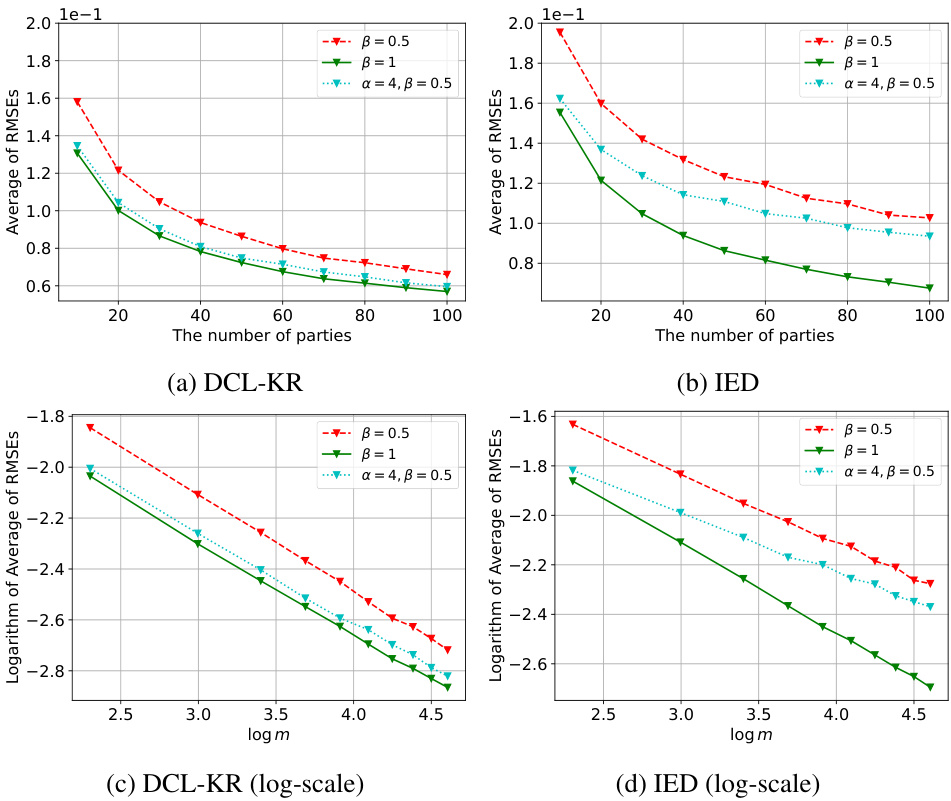
This figure compares the performance of IED and DCL-KR algorithms on the Toy-3D dataset when the distribution of public data (px) is different from the distribution of local data (px). The plots show the average root mean squared error (RMSE) against the number of parties (m) and the logarithm of the average RMSE against the logarithm of m. Different lines represent scenarios with varying parameters (α, β) controlling the relationship between px and px. The results demonstrate that DCL-KR maintains near-optimal convergence rates regardless of px, unlike IED.
More on tables
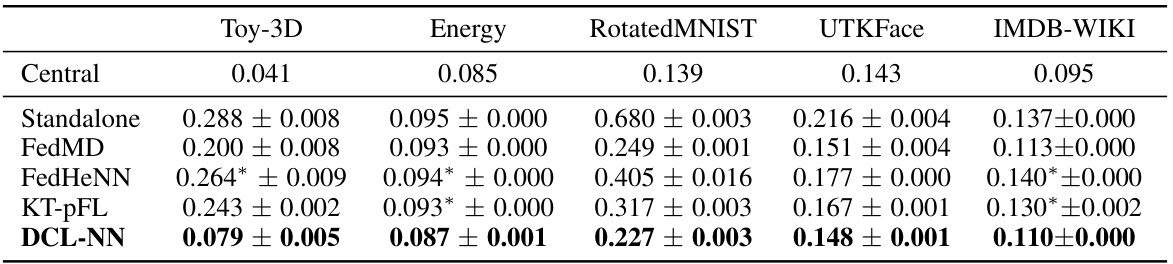
This table compares the performance of four different collaborative learning algorithms (FedMD, FedHeNN, KT-pFL, and DCL-NN) against standalone and centralized models on five regression datasets (Toy-3D, Energy, RotatedMNIST, UTKFace, and IMDB-WIKI). The results, presented as average RMSE and standard deviation, show that DCL-NN outperforms all baselines, demonstrating its effectiveness in collaborative learning settings.

This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve near minimax optimality without directly sharing private data or models. It considers factors such as interaction methods, local data privacy, distributed nature of data, and whether the data is independently and identically distributed (i.i.d.) or not. The table highlights that the proposed DCL-KR algorithm achieves nearly minimax optimality under heterogeneous conditions, unlike most existing methods.

This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve (near) minimax optimality while addressing challenges such as local data privacy, massively distributed data, and non-independent and identically distributed (non-i.i.d.) data. It highlights the unique features of each algorithm regarding data interaction methods and the types of decentralized environments they effectively handle.

This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve near-minimax optimality in various decentralized settings. It considers factors such as local data privacy, massive distribution, and non-i.i.d. (independent and identically distributed) data. The table highlights the algorithms’ success in these challenging environments while preserving local data privacy. Note that the nonparametric version of the FedAvg algorithm is included for comparison.
This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve (near) minimax optimality in various decentralized environments. It considers factors like the method of interaction between parties (e.g., divide-and-conquer, model exchange, knowledge distillation), whether local data privacy is preserved, whether the data is massively distributed, and whether the data is independently and identically distributed (i.i.d.) or not. The table highlights that the proposed DCL-KR algorithm is notable for achieving near minimax optimality without directly sharing local data or models, unlike many other approaches.
This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve (nearly) minimax optimality in various decentralized settings. It highlights whether each algorithm preserves local data privacy, handles massively distributed data, and tolerates non-identically independently distributed (non-i.i.d.) and unbalanced data.
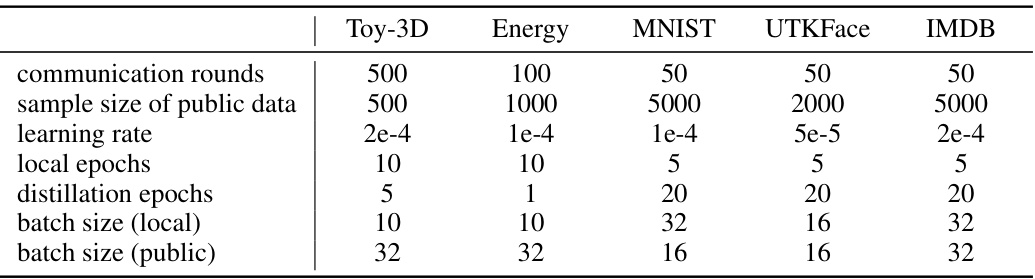
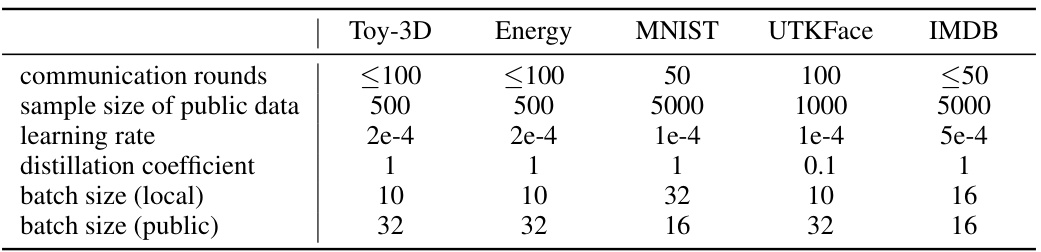
This table shows the hyperparameters used for the KT-pFL algorithm in the experiments. The hyperparameters include the number of communication rounds, sample size of public data, learning rate, distillation epochs, batch size (local), and batch size (public) for five datasets: Toy-3D, Energy, MNIST, UTKFace, and IMDB.

This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve (near) minimax optimality in various decentralized environments. It considers factors like data privacy, data distribution (i.i.d. or non-i.i.d.), and the scale of the distributed system. The table highlights whether each algorithm preserves local data privacy, handles massive datasets, manages non-identically independently distributed (non-i.i.d.) data across multiple parties, and achieves (near) minimax optimality.

This table compares several decentralized collaborative learning algorithms based on kernel regression, focusing on their ability to achieve near minimax optimality without directly sharing private data or models. It highlights the interaction methods (divide-and-conquer, model exchange, knowledge distillation), data privacy considerations, data distribution characteristics (massively distributed, non-i.i.d., unbalanced), and whether each algorithm achieves (near) minimax optimality. The table shows that the proposed DCL-KR algorithm using knowledge distillation is the only one that achieves near minimax optimality in massively distributed, statistically heterogeneous settings while preserving data privacy.
Full paper#