↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many researchers assume that large language models (LLMs) can implicitly learn the numerical constraints within data science application programming interfaces (APIs) to produce valid code. However, this paper empirically investigates the proficiency of LLMs in handling such constraints and finds that while LLMs excel at generating simple programs, their performance drastically declines when confronted with more complex or unusual inputs.
This research employed three evaluation settings: full programs, all parameters, and individual parameters of a single API. The results reveal that state-of-the-art LLMs, even GPT-4-Turbo, still struggle with arithmetic API constraints. The study introduces DSEVAL, a novel benchmark for systematically evaluating LLM capabilities in this area. DSEVAL provides a rigorous assessment of various LLMs and uncovers significant performance gaps, particularly highlighting the shortcomings of open-source models compared to their proprietary counterparts.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the common assumption that LLMs inherently understand numerical constraints in data science APIs. This finding has significant implications for the development and application of LLMs in data science, highlighting the need for more robust methods to ensure the validity and reliability of AI-generated code. Future research can explore techniques to improve LLM comprehension of numerical constraints or develop new methods for validating AI-generated code, ultimately boosting the trustworthiness of AI in data science.
Visual Insights#
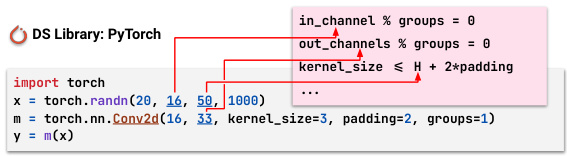
This figure shows a typical data science (DS) program built using the PyTorch library. It highlights the constraints that must be satisfied for the program to be valid. These constraints involve relationships between the input data properties (like its dimensions) and the parameters of the PyTorch Conv2d API (such as kernel size and padding). The example illustrates that satisfying these constraints is crucial for the correct execution of the DS program. The constraints are shown in a box on the right, illustrating how the numerical values must meet specific conditions.
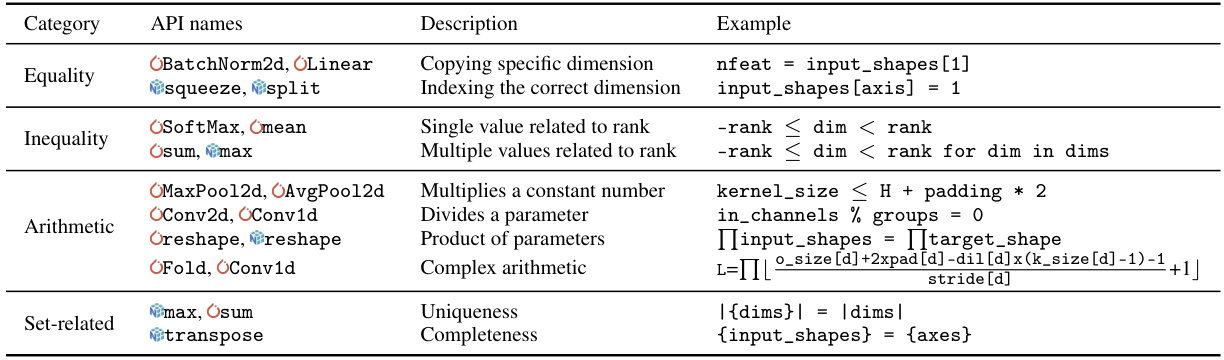
This table categorizes different types of constraints found in data science APIs, providing examples of APIs that exhibit each constraint type. The categories include Equality (where values must match exactly), Inequality (where values must be greater or less than), Arithmetic (constraints involving arithmetic operations), Set-related (constraints based on set properties), and Complex arithmetic (more intricate combinations of operations). For each category, example APIs are listed, and sample constraints are shown to illustrate their application.
In-depth insights#
LLM’s API grasp#
Analyzing LLMs’ understanding of Data Science (DS) APIs reveals a nuanced picture. While LLMs demonstrate proficiency in generating simple DS programs and correctly utilizing commonly-seen API patterns, their true comprehension of underlying numerical constraints is questionable. The ability to memorize common usage patterns from massive training data overshadows a genuine understanding of the mathematical and logical rules governing API parameters. This is particularly evident when dealing with more complex or unusual inputs, where performance significantly deteriorates. LLMs often resort to memorization of simple, frequently-encountered input-output pairs, neglecting the underlying arithmetic relationships. This highlights a critical limitation: while LLMs can mimic valid code generation superficially, they struggle to generalize their knowledge effectively, indicating a crucial gap between mimicking patterns and achieving genuine understanding of numerical API constraints. Future research should focus on developing LLMs that possess a deeper understanding of the mathematical and logical constraints inherent in DS APIs, moving beyond pattern recognition to true reasoning and problem-solving capabilities.
Constraint types#
The categorization of constraints in data science APIs is crucial for evaluating the capabilities of large language models (LLMs) in generating valid code. A thoughtful approach to constraint types reveals several key dimensions. Equality constraints, which require exact value matches, often involve shape consistency checks or index validation, highlighting the LLM’s proficiency in handling basic structural aspects of data. Inequality constraints, specifying value ranges (greater/less than), tend to be related to rank validation or dimension limits, presenting a more nuanced challenge that reveals the LLM’s grasp of dimensional data structures. Arithmetic constraints, involving numerical operations (modulo, division, etc.), pose the most significant hurdle and are indicative of true comprehension of the underlying mathematical properties; LLMs often struggle with these, highlighting a gap between pattern recognition and genuine mathematical understanding. Finally, set-related constraints address more complex relationships between data attributes, such as uniqueness or completeness checks. These constraints expose the LLMs’ ability to manage intricate logical connections, indicating a potential weakness for dealing with high level abstractions.
DSEVAL benchmark#
The DSEVAL benchmark emerges as a crucial contribution, systematically evaluating LLMs’ ability to grasp numerical constraints within Data Science APIs. Its strength lies in its comprehensive design, incorporating diverse APIs from popular libraries like PyTorch and NumPy, covering various constraint types (equality, inequality, arithmetic, set-related) and difficulty levels. DSEVAL’s methodology is rigorous, employing three distinct evaluation settings (full program, all parameters, individual parameter) to pinpoint LLM limitations. The benchmark’s lightweight validation, leveraging SMT solvers, enhances efficiency and scalability. The results reveal a significant performance gap between large proprietary models (like GPT-4-Turbo) and open-source models, highlighting the challenge of truly understanding underlying numerical constraints. DSEVAL’s public availability facilitates further research and improvements in LLM code generation, thereby paving the way for more robust and reliable DS applications.
LLM limitations#
Large language models (LLMs) demonstrate impressive capabilities in code generation, but their understanding of numerical constraints within data science APIs remains limited. LLMs struggle with complex or unusual input data, often relying on memorized patterns from training data rather than genuine comprehension of underlying mathematical rules. Their performance degrades significantly as input complexity increases, highlighting a lack of robust generalization. While advanced models like GPT-4-Turbo show higher overall accuracy, they still struggle with intricate arithmetic constraints. The reliance on memorization and pattern matching, rather than true understanding, leads to a significant performance gap between the most advanced LLMs and open-source alternatives. This suggests that future research should focus on improving LLMs’ capacity for true mathematical reasoning rather than solely enhancing pattern recognition capabilities. Furthermore, the creation of more comprehensive benchmarks is crucial for objectively evaluating these limitations and guiding future development.
Future work#
Future research could explore several promising avenues. Expanding the benchmark (DSEVAL) to encompass a wider array of DS libraries and APIs is crucial to enhance its generalizability and impact. Investigating the effectiveness of various prompting techniques, such as chain-of-thought prompting or different instruction-tuning strategies, on improving LLMs’ comprehension of numerical constraints is warranted. A deeper investigation into the interplay between LLM architecture, training data, and the ability to satisfy API constraints would reveal valuable insights into model limitations and opportunities for improvement. Furthermore, exploring the potential of incorporating symbolic reasoning or formal methods into LLMs to enhance their understanding of numerical constraints is a significant area of future work. Developing hybrid approaches that combine the strengths of LLMs with formal verification techniques could lead to more reliable and robust DS code generation. Finally, research into the ethical implications of using LLMs for DS code generation and the development of mitigation strategies for potential misuse is vital.
More visual insights#
More on figures
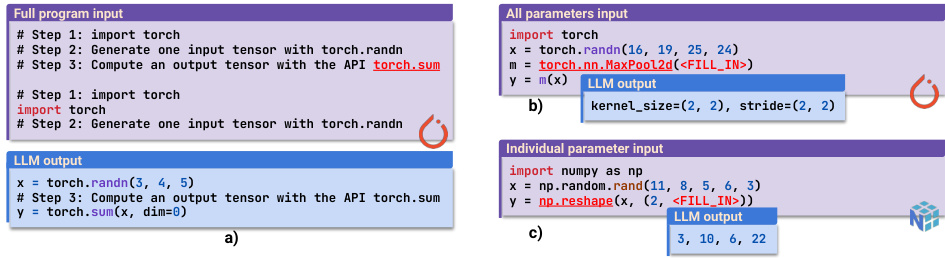
This figure shows three different settings used to evaluate the performance of LLMs in handling numeric constraints in data science APIs. The settings vary in the level of detail provided to the LLM and the complexity of the task: 1) Full program: The LLM is asked to generate a complete DS program, including importing the necessary libraries and creating an input tensor. 2) All parameters: The LLM is provided with the input data and is only asked to generate the API parameters. 3) Individual parameter: The LLM is given the input data and all but one parameter and asked to predict only the missing parameter value. This figure also presents example problem inputs, expected outputs and the actual LLMs’ outputs for each of the three settings.

The figure shows how the authors use SMT solvers (Z3 and CVC5) to generate valid inputs and validate the outputs of LLMs. Panel (a) illustrates input generation: SMT solvers check if a set of constraints (encoded as a formula) is satisfiable given concrete input values and symbolic variables representing the parameters that the LLM needs to predict. If satisfiable, the input is valid for the LLM. Panel (b) illustrates output validation: SMT solvers verify if the concrete values predicted by the LLM satisfy the constraints given the concrete input values. This process ensures that the input and output data used for evaluating the LLMs’ performance are valid and properly constrained.
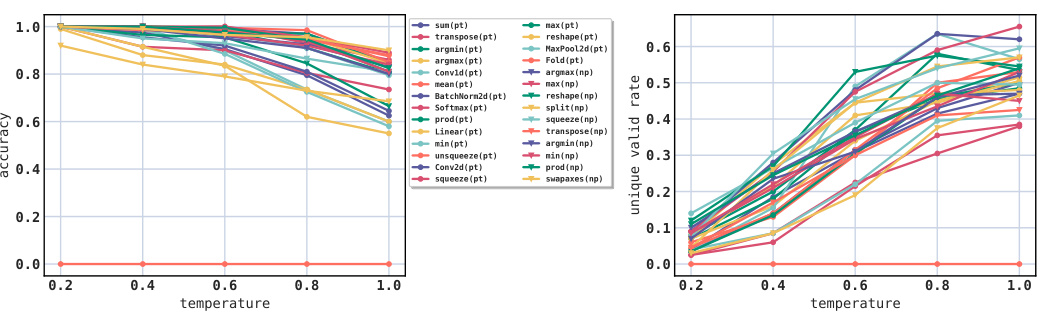
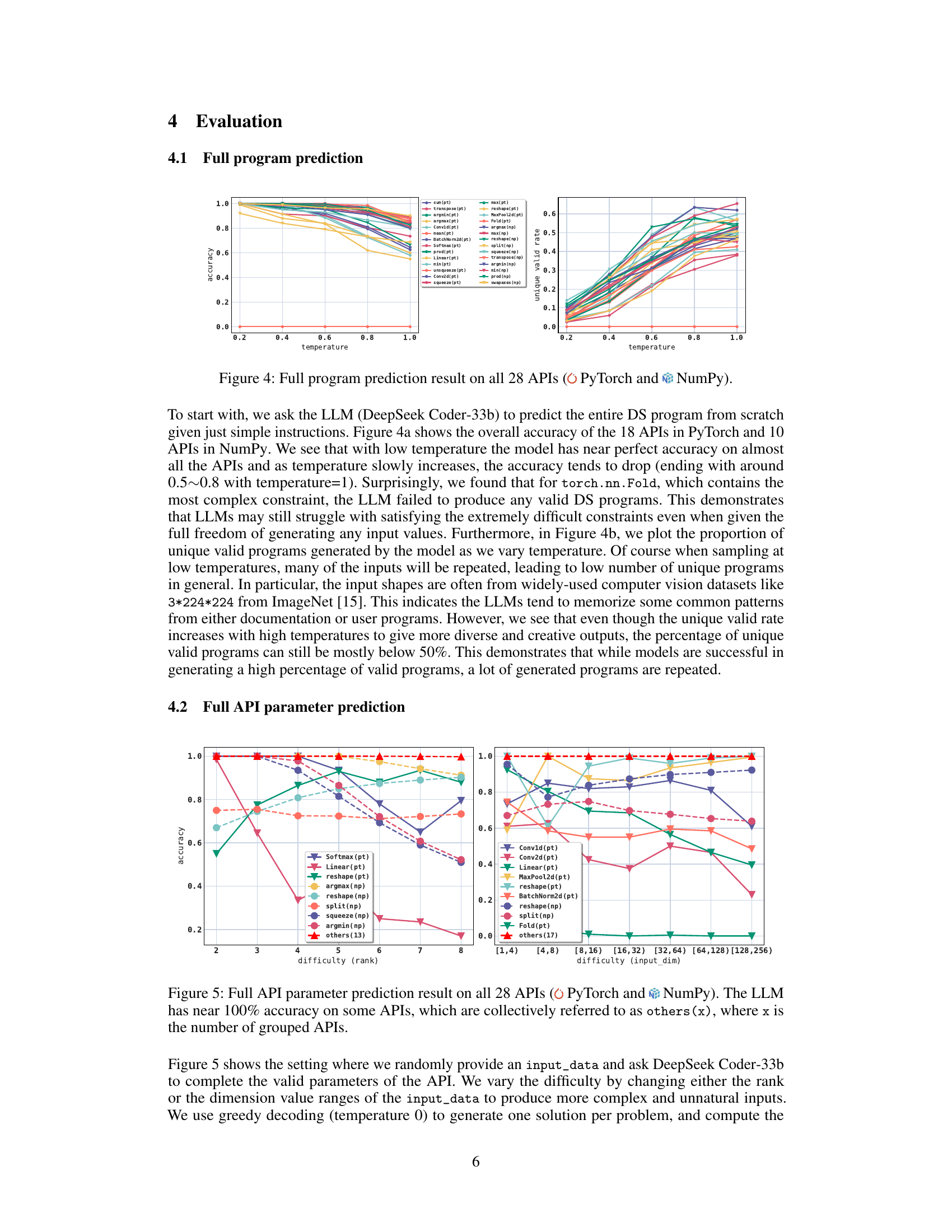
This figure shows the results of the full program prediction experiment on 28 APIs from PyTorch and NumPy libraries. The x-axis represents the temperature used during LLM sampling, and the y-axis shows both the accuracy of the generated programs (left panel) and the unique valid rate (right panel). Each line in the graph represents a different API. The results illustrate that LLMs achieve near-perfect accuracy with low temperatures but that performance decreases as temperature increases. The unique valid rate also increases with higher temperature, indicating that higher temperatures lead to more diverse outputs, but that still a significant number of programs are repetitive.
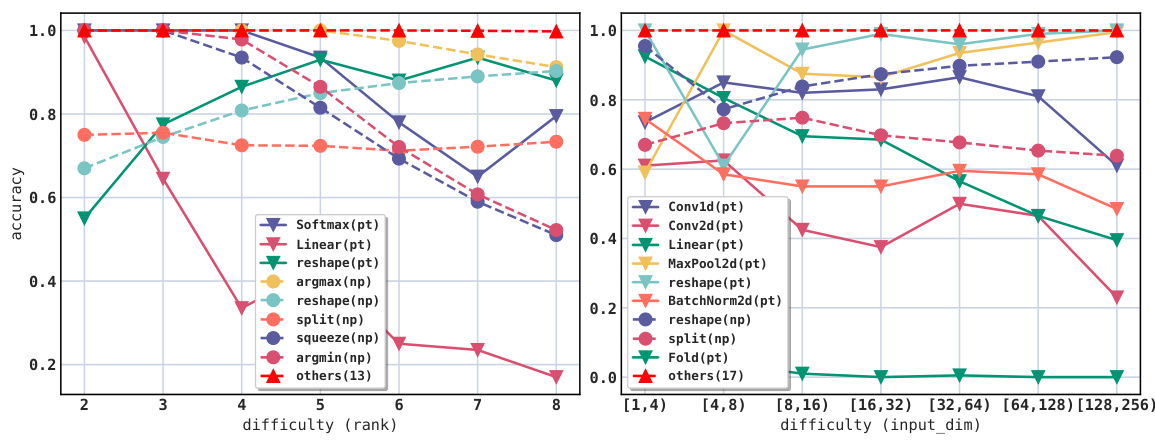
This figure displays the results of the full API parameter prediction experiment. The experiment tested the ability of a large language model (LLM) to predict all the parameters for 28 APIs (18 from PyTorch and 10 from NumPy) given input data. The difficulty of the task was varied by adjusting the rank (number of dimensions) and dimension values of the input data. The figure shows the accuracy of the LLM across different difficulty levels. The observation that some APIs show near-perfect accuracy highlights the LLM’s ability to perform well on common or simpler API calls and that the difficulty increases with more complex inputs.
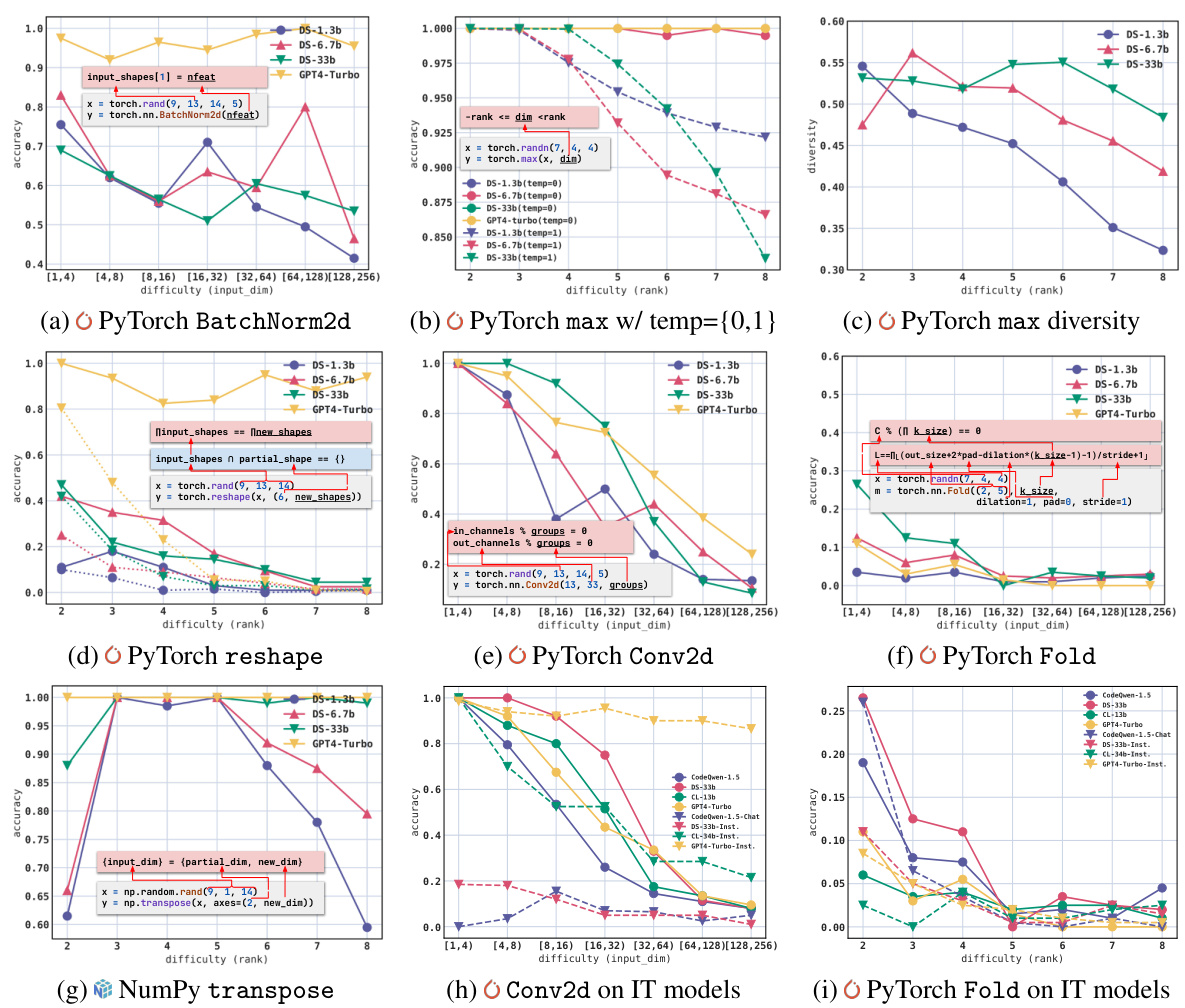
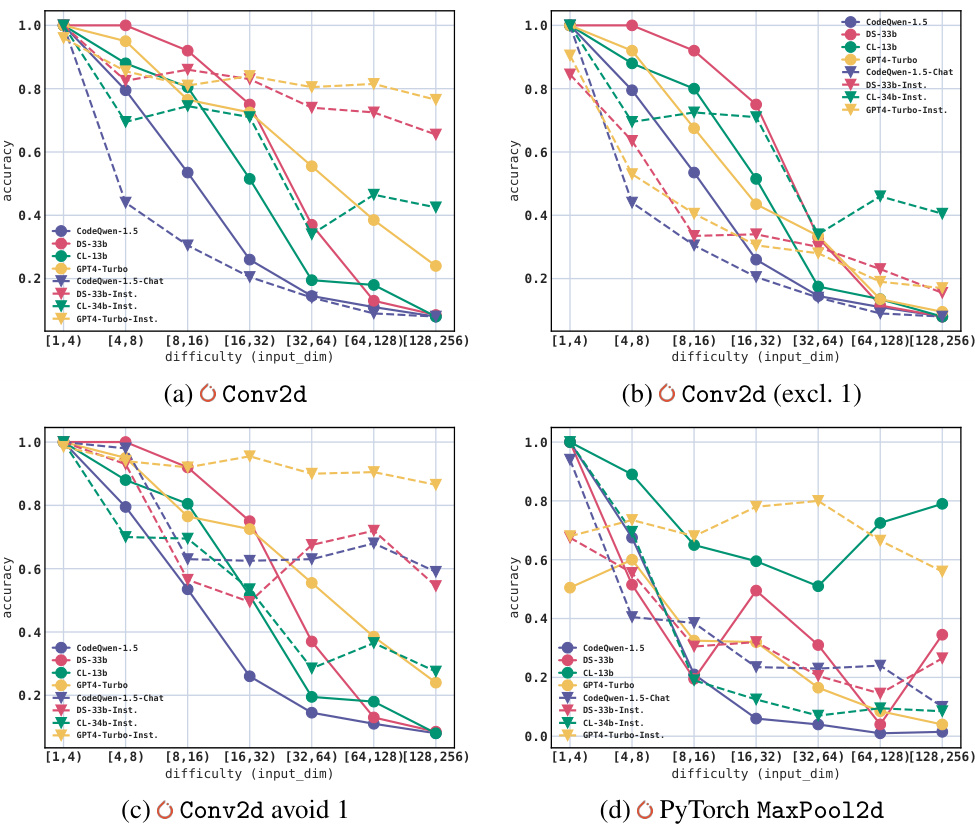
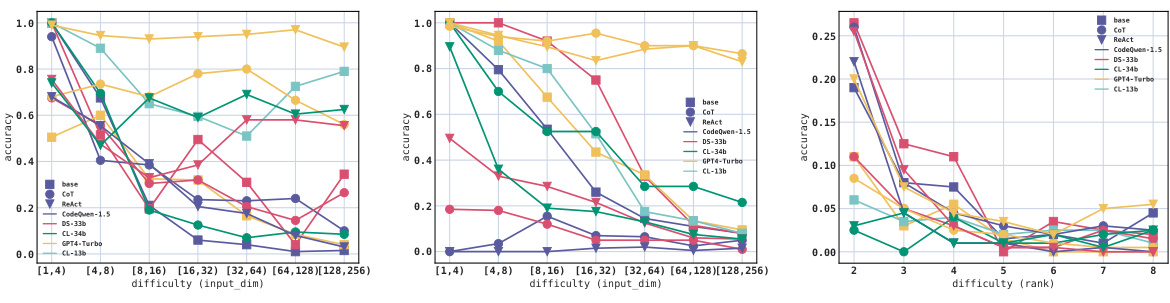
This figure displays the results of experiments focusing on a single API parameter prediction. It presents accuracy metrics for various LLMs across different difficulty levels and constraint types (equality, inequality, arithmetic, set-related). The use of different line styles and the references to the appendices highlight the nuanced methods and additional results detailed elsewhere in the paper.
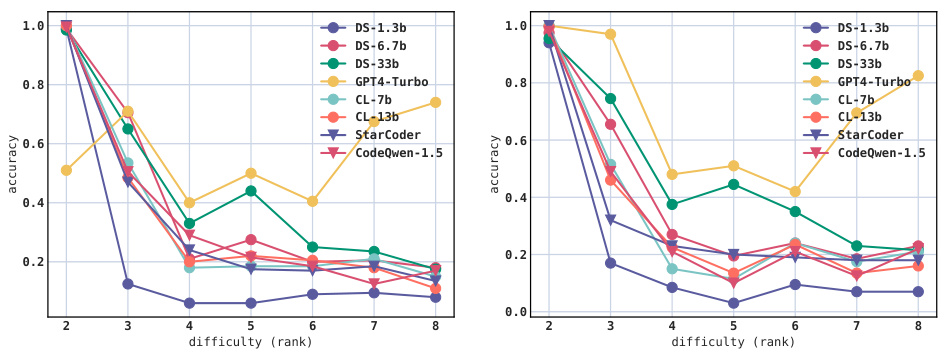
This figure shows the accuracy of LLMs in predicting all the parameters of 28 APIs (18 from PyTorch and 10 from NumPy) when given the input data. The difficulty is varied by changing either the rank or the dimension of the input data. The results show that while LLMs perform well on simple APIs, their accuracy drops significantly as the difficulty increases. Some APIs consistently maintain high accuracy regardless of difficulty, which are grouped together in the legend.

This figure shows an example of GPT-4-Turbo’s incorrect response in a code generation task. Instead of correctly using the input tensor’s last dimension as the
in_featuresparameter for atorch.nn.Linearlayer, GPT-4-Turbo incorrectly flattens the input tensor before applying the linear layer. This demonstrates a failure to correctly understand and apply the API’s constraints, highlighting a limitation of the model’s ability to reason about numerical constraints in code generation.
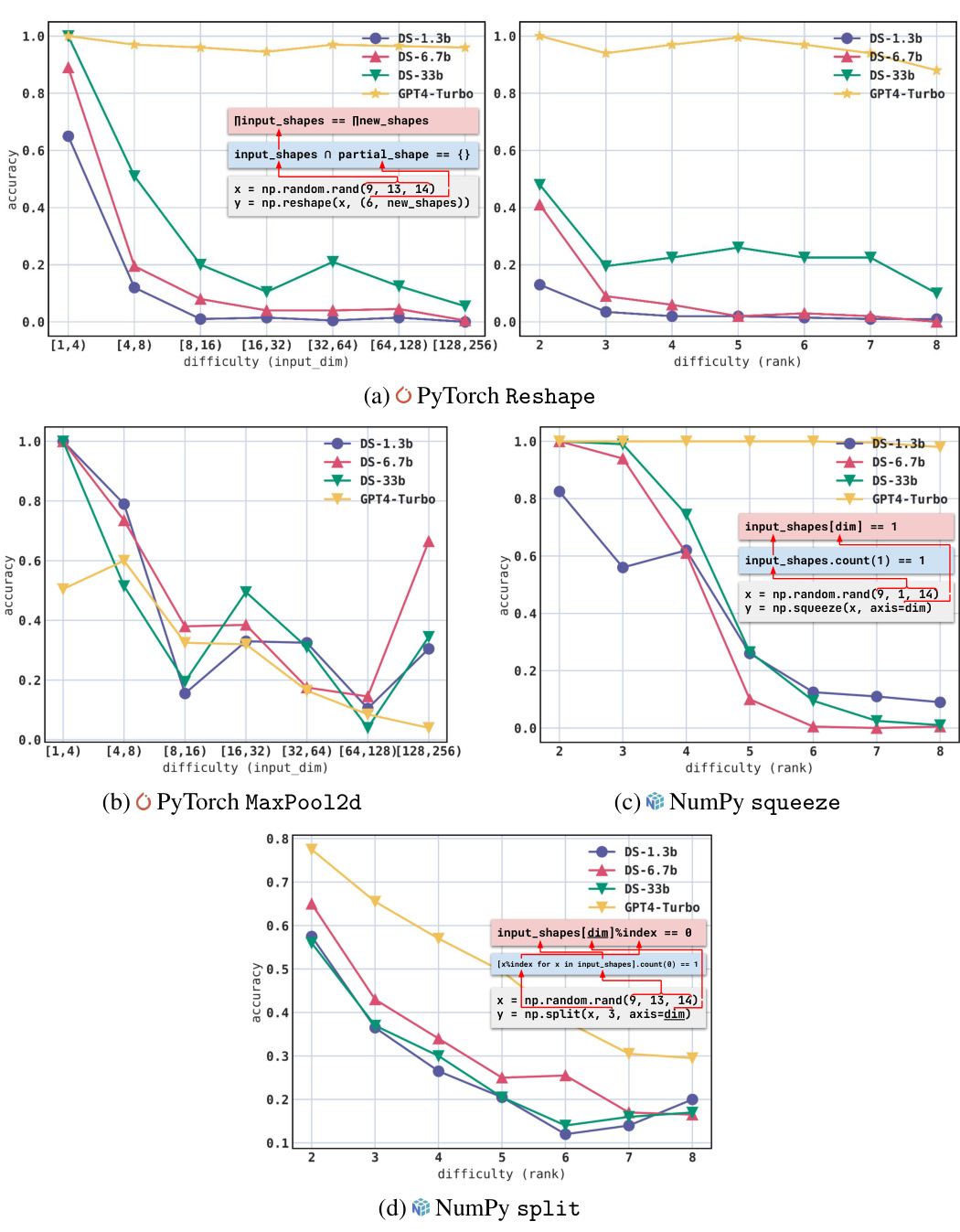
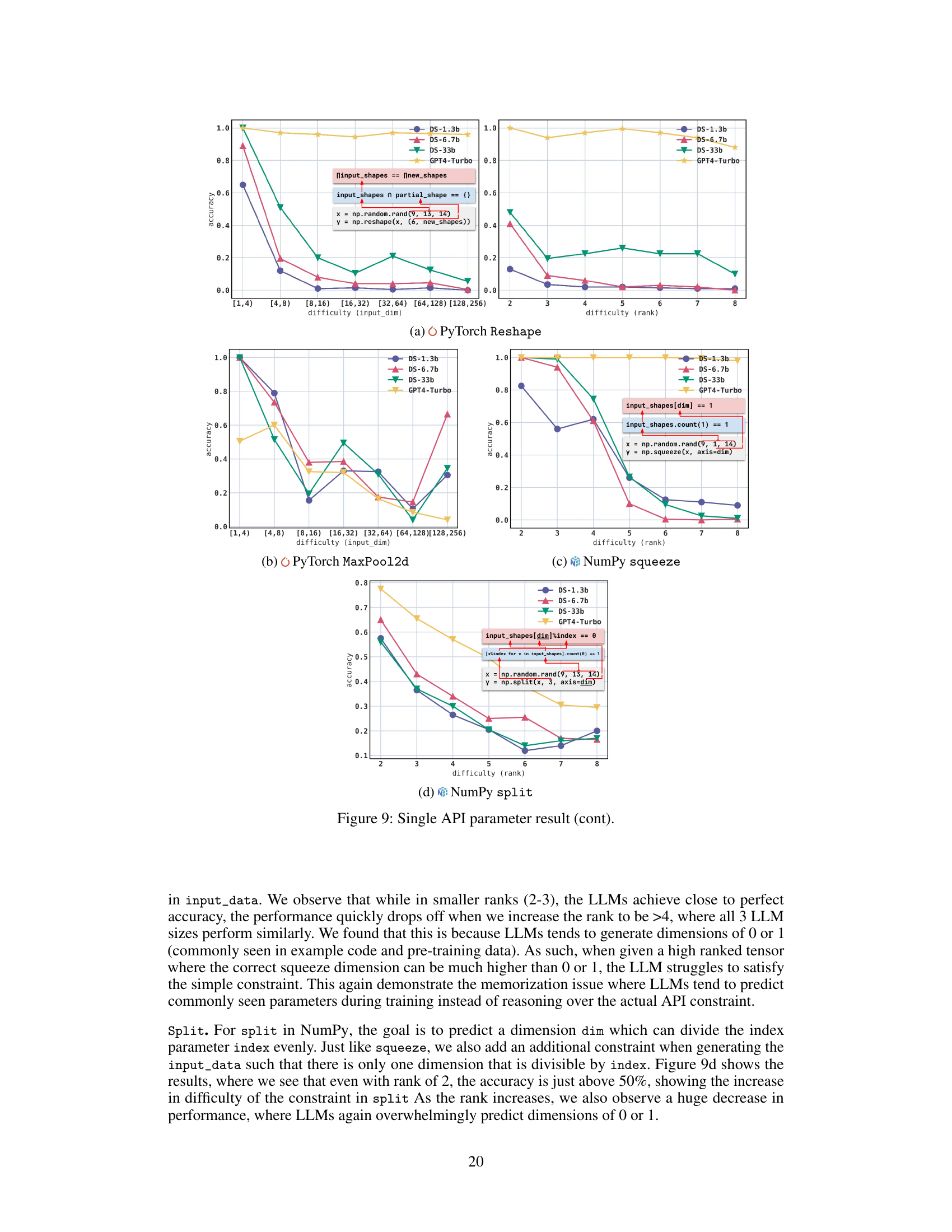
The figure shows the accuracy of different LLMs across various difficulty levels for four different APIs: PyTorch Reshape, PyTorch MaxPool2d, NumPy squeeze, and NumPy split. Each subfigure shows how accuracy changes as the difficulty (input dimension or rank) increases. The results highlight the challenges LLMs face in handling diverse numerical constraints within single API parameters.

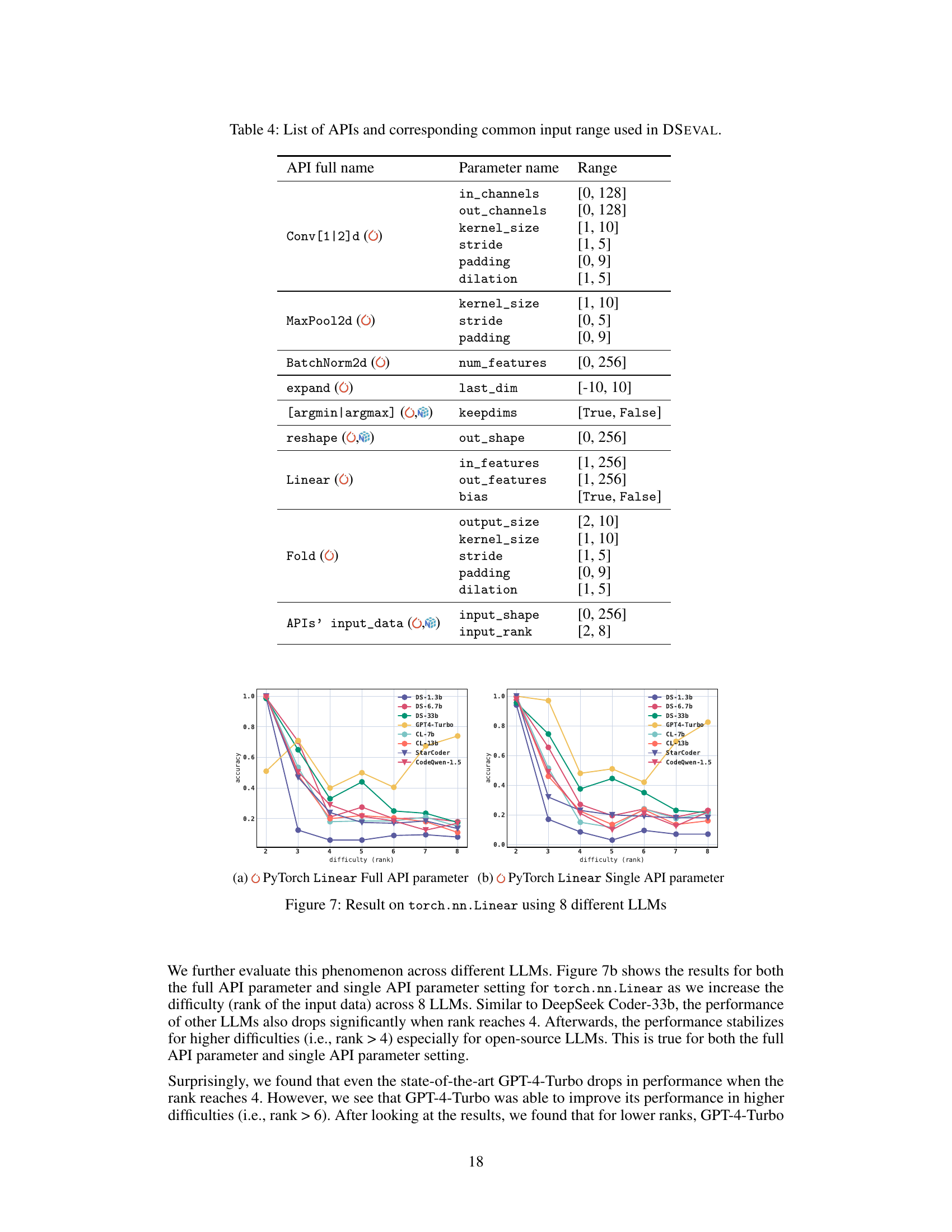
This figure shows the results of using 8 different LLMs on the torch.nn.Linear API in two different settings: full API parameter and single API parameter. The x-axis represents the difficulty (rank of the input tensor). The y-axis represents the accuracy of the models. The figure demonstrates that the performance of all models drop when the rank reaches 4, and then stabilizes for higher ranks, especially for open-source LLMs. The result shows the difference between the performance of different LLMs in handling different difficulty levels.

This figure shows the accuracy of the DeepSeek Coder-33b model in predicting the full API parameters for 28 different APIs from PyTorch and NumPy libraries. The difficulty of prediction is systematically varied by adjusting the rank (number of dimensions) and dimension values (size along each dimension) of the input data. The graph displays how accuracy changes across different difficulty levels. The figure highlights that while some APIs show near-perfect accuracy, others demonstrate a significant drop in performance as the difficulty increases.
This figure shows the accuracy and unique valid rate for 28 APIs (18 from PyTorch and 10 from NumPy) when LLMs generate complete DS programs from scratch with varying temperature. The results demonstrate that LLMs achieve near-perfect accuracy at low temperatures but the performance decreases as the temperature increases. The unique valid rate is also plotted, showing that LLMs tend to memorize common patterns instead of genuinely understanding the underlying constraints. This indicates that the ability of LLMs to generate programs that satisfy complex constraints is limited.
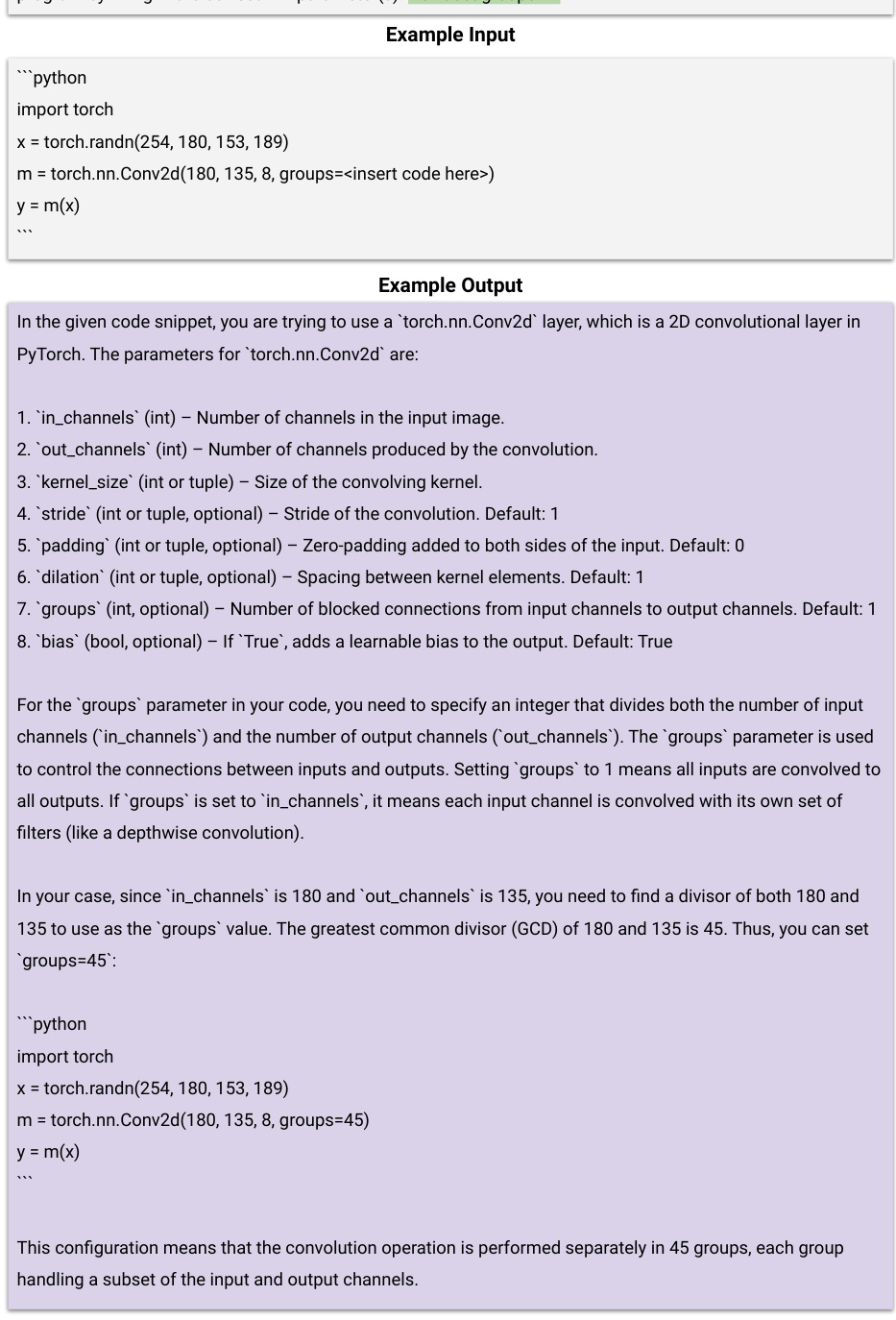
This figure displays the results of experiments using instruction-tuned LLMs on three different settings for the Conv2d API. The first setting (a) includes all answers, while the second (b) excludes groups=1 as correct. The third (c) is similar to (b) but with an additional instruction in the prompt. It demonstrates how the additional instruction affects the performance and the impact of excluding groups=1.

This figure presents the results of the full API parameter prediction experiment on 28 APIs from PyTorch and NumPy. The x-axis shows the difficulty level, increasing from left to right. The y-axis represents the accuracy of the LLM in predicting the correct API parameters given input data with varying levels of complexity. Some APIs showed nearly perfect accuracy regardless of difficulty, while many others showed a significant decrease in accuracy as the difficulty increased. The ‘others(x)’ group indicates APIs that performed well across all difficulty levels.
This figure displays the results of the full API parameter prediction experiment on 28 APIs from PyTorch and NumPy. The x-axis shows the difficulty level, which was varied by changing either the rank or dimension values of the input data. The y-axis represents the accuracy achieved by the LLM in predicting the correct API parameters. The figure reveals near-perfect accuracy on several APIs (grouped as ‘others(x)’), suggesting that these APIs might have simpler or more commonly observed constraint patterns. However, for other APIs, accuracy noticeably decreases as the difficulty increases, demonstrating the challenge of handling complex constraints for LLMs.

The figure shows the accuracy of the DeepSeek Coder-33b model in predicting all API parameters given different input data for 28 APIs from PyTorch and NumPy libraries. The difficulty of the task is varied by changing the rank or the dimension values of the input data. The results show that the model performs well on simple APIs but struggles with more complex or uncommon inputs.

This figure shows the results of evaluating LLMs on predicting the parameters of 28 APIs from PyTorch and NumPy when the input data is provided. The difficulty of the task is varied by changing the rank or dimension values of the input data. The LLM achieves near-perfect accuracy on some easier APIs, while the accuracy drops significantly on more complex APIs as the difficulty increases.
More on tables
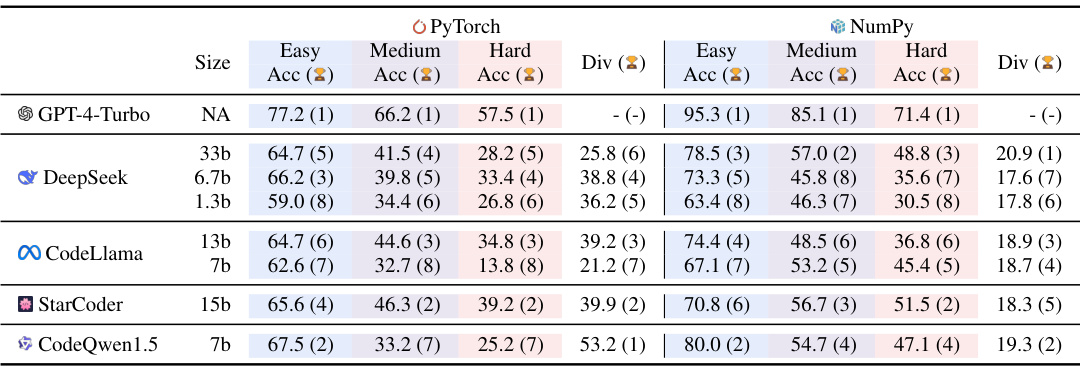
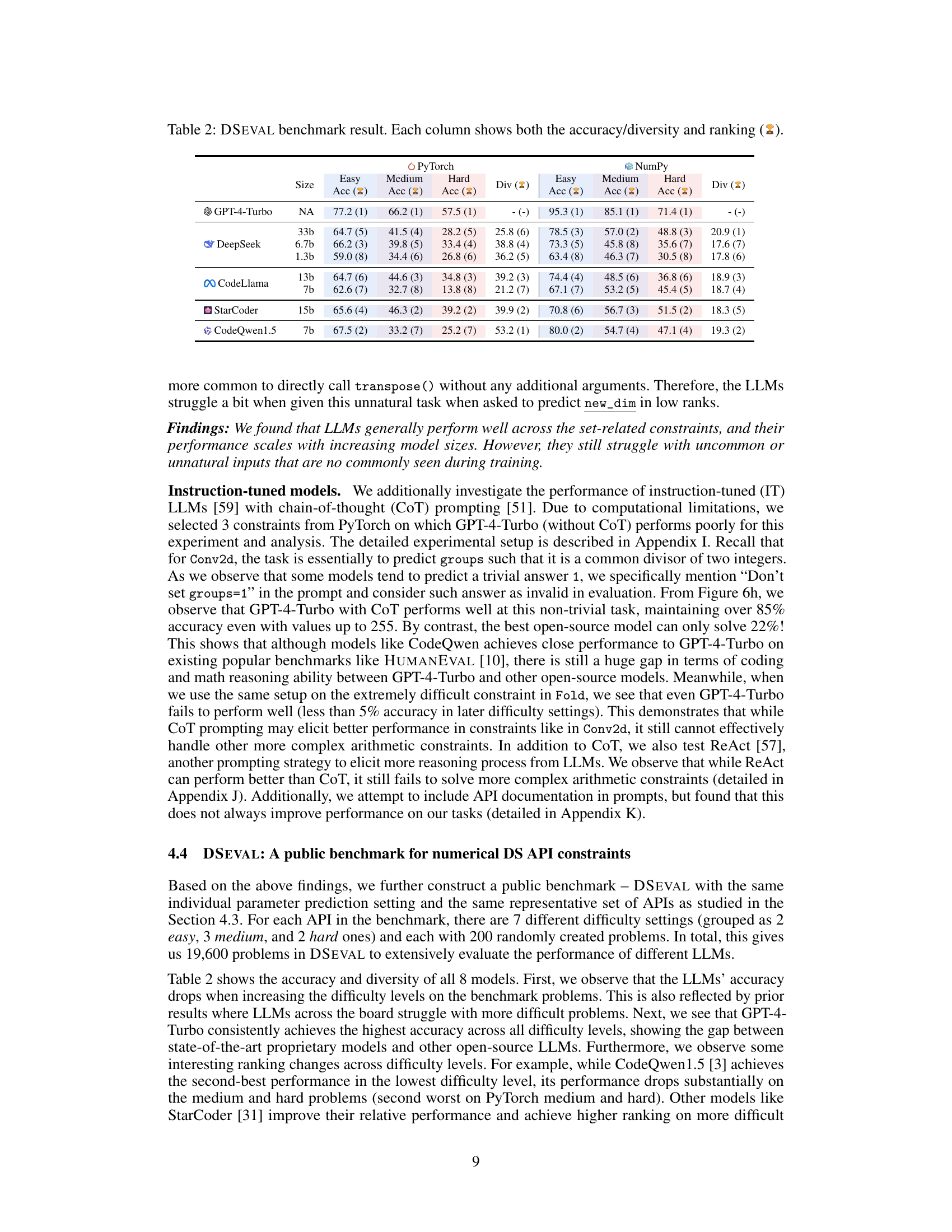
This table presents the results of the DSEVAL benchmark, which evaluates the performance of eight different LLMs on various data science APIs with different difficulty levels. Each LLM’s performance is assessed based on its accuracy and diversity in generating correct parameters for PyTorch and NumPy APIs. The table shows accuracy scores for easy, medium, and hard difficulty levels, as well as diversity scores and rankings for each model across these difficulty levels. The rankings indicate the relative performance of each LLM compared to others.

This table lists the twelve APIs used in the DSEVAL benchmark, their corresponding constraints, and the category to which each constraint belongs. The APIs are drawn from PyTorch and NumPy, and the constraints encompass various types, including equality, inequality, and arithmetic relationships between API parameters and input data properties. This table is crucial for understanding the scope and complexity of the constraints the LLMs were evaluated on in the DSEVAL benchmark.

This table lists the 12 APIs used in the DSEVAL benchmark, along with the range of common input values for each API’s parameters. The purpose is to define the input space for testing the LLMs’ ability to handle various input scenarios, thus controlling the difficulty level of the experiments. Each API has several parameters, and the table provides a common range for those parameters which are not directly involved in the constraint being tested.
Full paper#