TL;DR#
Many machine learning models rely on solving minimax optimization problems, which present unique challenges in nonconvex and nonsmooth settings. Existing methods often struggle with efficiency and theoretical guarantees in these complex scenarios, particularly when stochasticity or large datasets are involved. The lack of efficient and theoretically sound algorithms hinders progress in various applications like GANs and reinforcement learning.
This paper addresses these challenges by proposing novel shuffling gradient-based methods. Two algorithms are developed: one for nonconvex-linear minimax problems and another for nonconvex-strongly concave settings. Both algorithms use shuffling strategies to construct unbiased estimators for gradients, resulting in improved performance and theoretical guarantees. The paper rigorously proves the state-of-the-art oracle complexity of these methods and demonstrates their effectiveness through numerical examples, showing they achieve comparable performance to existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in nonconvex-concave minimax optimization. It introduces novel shuffling gradient-based methods that achieve state-of-the-art oracle complexity, improving upon existing techniques. The findings open avenues for further research on variance reduction, especially in the context of minimax problems with nonsmooth terms, and have significant implications for advancing machine learning algorithms.
Visual Insights#

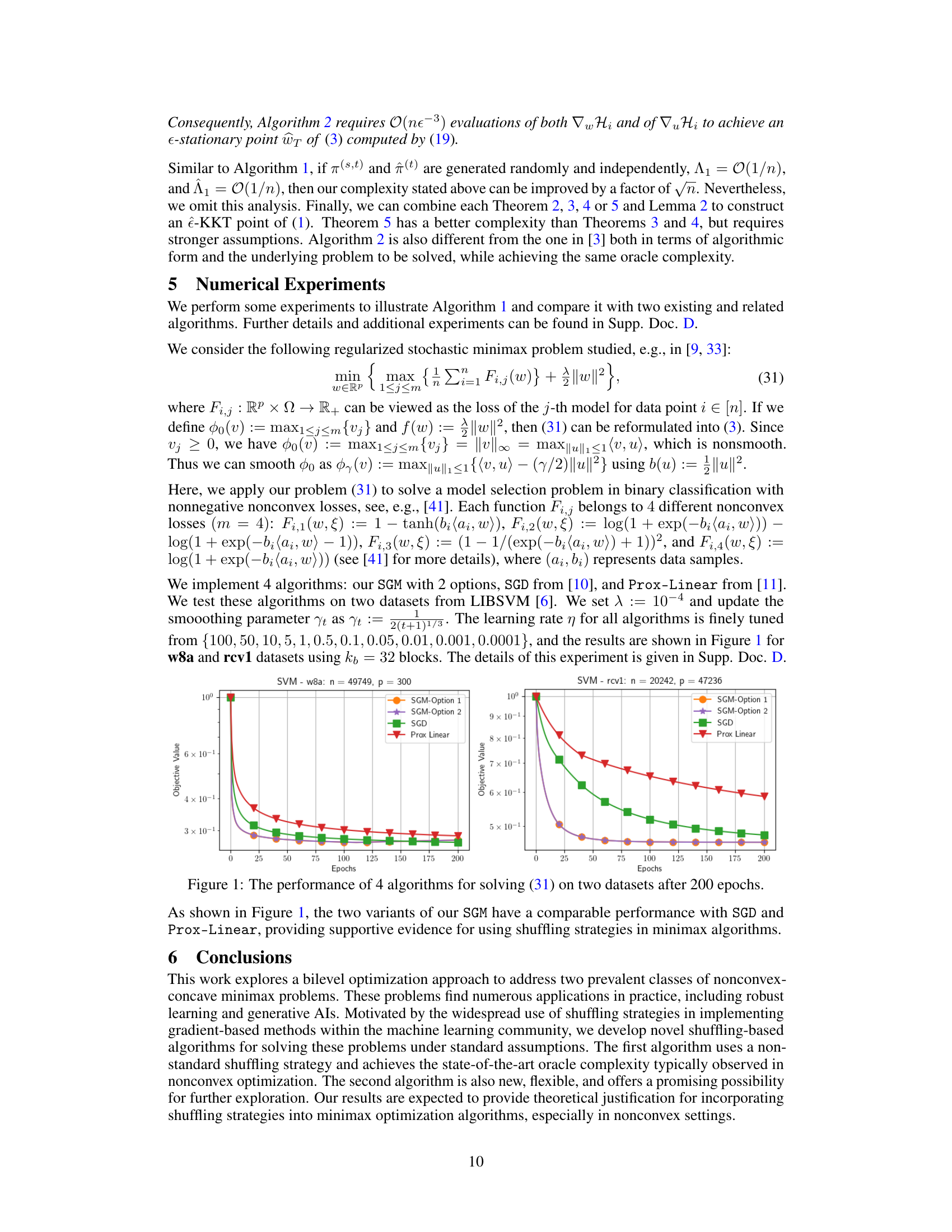
🔼 This figure compares the performance of four different algorithms on two datasets (w8a and rcv1) after 200 epochs. The algorithms compared are two variants of the proposed Shuffling Gradient Method (SGM), standard Stochastic Gradient Descent (SGD), and Prox-Linear. The y-axis represents the objective value, and the x-axis shows the number of epochs. The figure visually demonstrates the relative performance of each algorithm in minimizing the objective function for the model selection problem in binary classification with nonnegative nonconvex losses, as described in the paper.
read the caption
Figure 1: The performance of 4 algorithms for solving (31) on two datasets after 200 epochs.
Full paper#