↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current methods for video inverse problems using image diffusion models often lead to issues like flickering and temporal inconsistencies in the generated videos. This is mainly because these methods treat each frame independently, ignoring the inherent temporal correlations within a video sequence. The paper argues that a more effective approach is to consider frames as continuous functions and videos as sequences of warping transformations.
The proposed solution, named Warped Diffusion, uses function space diffusion models to overcome these challenges. It introduces a simple yet powerful test-time guidance mechanism to ensure temporal consistency. By viewing videos as sequences of continuous warping transformations, the method leverages state-of-the-art image diffusion models like Stable Diffusion XL to generate temporally consistent video outputs. Experimental results show Warped Diffusion outperforms existing approaches, showcasing enhanced performance on video inpainting and super-resolution tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel framework for applying image diffusion models to video inverse problems. This is crucial because existing methods often struggle with temporal consistency in video generation. The proposed approach, Warped Diffusion, is versatile, working with various image diffusion models and solving various video problems, like inpainting and super-resolution, by making the models temporally consistent and outperforming existing methods. It opens doors for future research on utilizing readily available image models effectively for video applications and addressing the temporal consistency challenges that limit video generation quality.
Visual Insights#

This figure displays the results of a video inpainting task. The top row shows the input video frames with a portion of each frame masked. The middle row shows the results generated by the ‘How I Warped Your Noise’ method, and the bottom row presents the results obtained using the proposed ‘Warped Diffusion’ method. The figure demonstrates that even with smooth shifting in the input video, the ‘Warped Diffusion’ method effectively maintains consistent and coherent inpainting across frames, unlike the ‘How I Warped Your Noise’ method which shows some inconsistency.

This table presents the quantitative results of single-frame evaluation for super-resolution and inpainting models. The models were trained with either independent noise or correlated noise from a Gaussian Process. The evaluation metrics include FID, Inception Score, CLIP Text Score, CLIP Image Score, SSIM, LPIPS, and MSE. Higher scores for Inception, CLIP Text Score, CLIP Image Score and SSIM indicate better performance; lower scores for FID, LPIPS and MSE indicate better performance. The results show that finetuning with correlated noise does not compromise performance, and GP models slightly outperform models trained with independent noise in the inpainting task.
In-depth insights#
Function Space DMs#
Function space diffusion models (DMs) offer a powerful approach to video generation and manipulation by treating video frames as continuous functions. This contrasts with traditional frame-by-frame methods, which often suffer from temporal inconsistencies. The key advantage lies in the inherent ability to model temporal correlations directly within the function space, leading to smoother, more realistic videos. By employing techniques like Gaussian processes to sample noise functions, these models elegantly handle the infinite-dimensional nature of continuous image representations. Furthermore, ensuring equivariance under warping transformations is crucial for temporal consistency and this can be achieved through specialized sampling mechanisms like self-guidance during inference. Equivariance guarantees that the model’s output is consistent with the warping of the input, preventing flickering and other artifacts. Although computationally more expensive than some traditional methods, the gains in temporal coherence and the potential for leveraging pre-trained image DMs make function space DMs a promising direction for video processing tasks.
Equivariance Guidance#
The concept of ‘Equivariance Guidance’ in the context of video generation using diffusion models addresses a critical challenge: maintaining temporal consistency. Naively applying image diffusion models frame-by-frame often results in flickering artifacts and temporal inconsistencies. Equivariance Guidance aims to enforce temporal coherence by ensuring the generated frames behave consistently under warping transformations—a key aspect of video, representing movement and deformation. This is achieved by guiding the diffusion model’s sampling process toward solutions that remain consistent across frames when subjected to these transformations, as defined by optical flow. The method cleverly leverages the power of existing image diffusion models without requiring extensive retraining on video data, making it a practical and efficient approach. By ensuring equivariance, the method aims to generate videos that are temporally coherent, resolving the flickering and texture inconsistencies frequently seen in naive frame-by-frame applications of image diffusion models to video. The core idea is to seamlessly incorporate temporal consistency during inference, leading to improved visual quality and more realistic video results. This technique fundamentally addresses a core limitation of directly applying image models to video, improving the quality and robustness of video generation. The effectiveness of this approach highlights the potential of cleverly adapting image-based methods for video processing tasks.
GP Noise Warping#
The proposed method of ‘GP Noise Warping’ offers a novel approach to address temporal inconsistencies in video generation using image diffusion models. Instead of relying on simplistic noise transformations like resampling or interpolation which often lead to blurry or unrealistic results, this method leverages the power of Gaussian Processes (GPs). GPs allow for continuous evaluation of the noise function at arbitrary locations, overcoming limitations of methods that operate solely on discrete grid points. By defining images and noise as functions and the generator as a mapping between functional spaces, the warping is done directly in the function space, leading to a more principled and robust handling of spatial transformations inherent in video sequences. This approach elegantly tackles both interpolation and inpainting challenges, resulting in superior video quality. Equivariance self-guidance, a post-hoc sampling mechanism, further enhances the temporal coherence by enforcing consistency under warping transformations. This eliminates the need for extensive video data training, making the approach versatile and practical.
Video Restoration#
Video restoration, a crucial aspect of video processing, aims to recover degraded video quality. Effective restoration tackles various issues, including noise reduction, blur mitigation, and artifact removal. Current approaches leverage advanced techniques like deep learning models, particularly diffusion models, to achieve high-quality results. These models can learn complex mappings between degraded and pristine video frames. However, naive applications often struggle with temporal consistency, leading to flickering artifacts and inconsistencies across frames. Advanced methods address this challenge by incorporating temporal information, for instance, using optical flow to align frames or employing recurrent neural networks to capture temporal dependencies. The choice of model architecture significantly impacts the quality and computational cost of the restoration process. Equivariance, the property of a model to maintain consistent output under transformations, is also important to ensure smooth, natural-looking restorations. Future directions include developing more efficient models capable of handling high-resolution videos in real-time, as well as addressing more challenging degradation types. Furthermore, investigating the integration of other modalities, such as audio and text, could lead to further improvements in the accuracy and fidelity of video restoration. Ultimately, the goal is to develop robust and versatile video restoration methods that can seamlessly integrate into various video applications.
Future Work#
Future research directions stemming from this work on Warped Diffusion could explore several promising avenues. Improving efficiency is paramount; the current method’s computational demands limit its applicability to longer videos. Investigating more efficient optical flow estimation techniques or exploring alternative warping strategies could significantly reduce processing time. Extending the model’s capacity to handle more complex transformations and scenarios, such as those involving occlusions or significant viewpoint changes, is crucial. The current approach relies heavily on accurate optical flow estimation; robustness to noisy or incomplete flow fields needs further development. Generalizing the approach beyond inpainting and super-resolution to encompass other video inverse problems, like denoising or deblurring, represents another valuable direction. Finally, a deeper theoretical analysis of the relationship between equivariance and temporal consistency in function space diffusion models could yield significant insights and potentially lead to more principled and robust methods. The investigation into alternative functional representations beyond Gaussian processes could enhance model flexibility and performance.
More visual insights#
More on figures

This figure illustrates the Warped Diffusion method applied to video super-resolution. It shows the process, starting with a function space diffusion model trained on images and Gaussian process samples. Optical flow is used to warp the GP samples from the previous frame to the current frame. Equivariance self-guidance is used in the ODE sampler to ensure temporal consistency in the output high-resolution frames.

This figure illustrates the Warped Diffusion framework for video super-resolution. It shows how a function space diffusion model is extended from images to videos using optical flow to warp Gaussian process samples between frames. Equivariance self-guidance ensures temporal consistency in the generated video.

This figure illustrates the Warped Diffusion method applied to video super-resolution. It shows the process in four steps: (a) A function space diffusion model is used to super-resolve images from Gaussian process samples. (b) Optical flow is used to extract warping transformations between consecutive input video frames. (c) These transformations are then used to warp the Gaussian process samples from the previous frame. (d) Equivariance self-guidance is introduced in the ODE sampler to maintain temporal consistency in the generated high-resolution video frames.

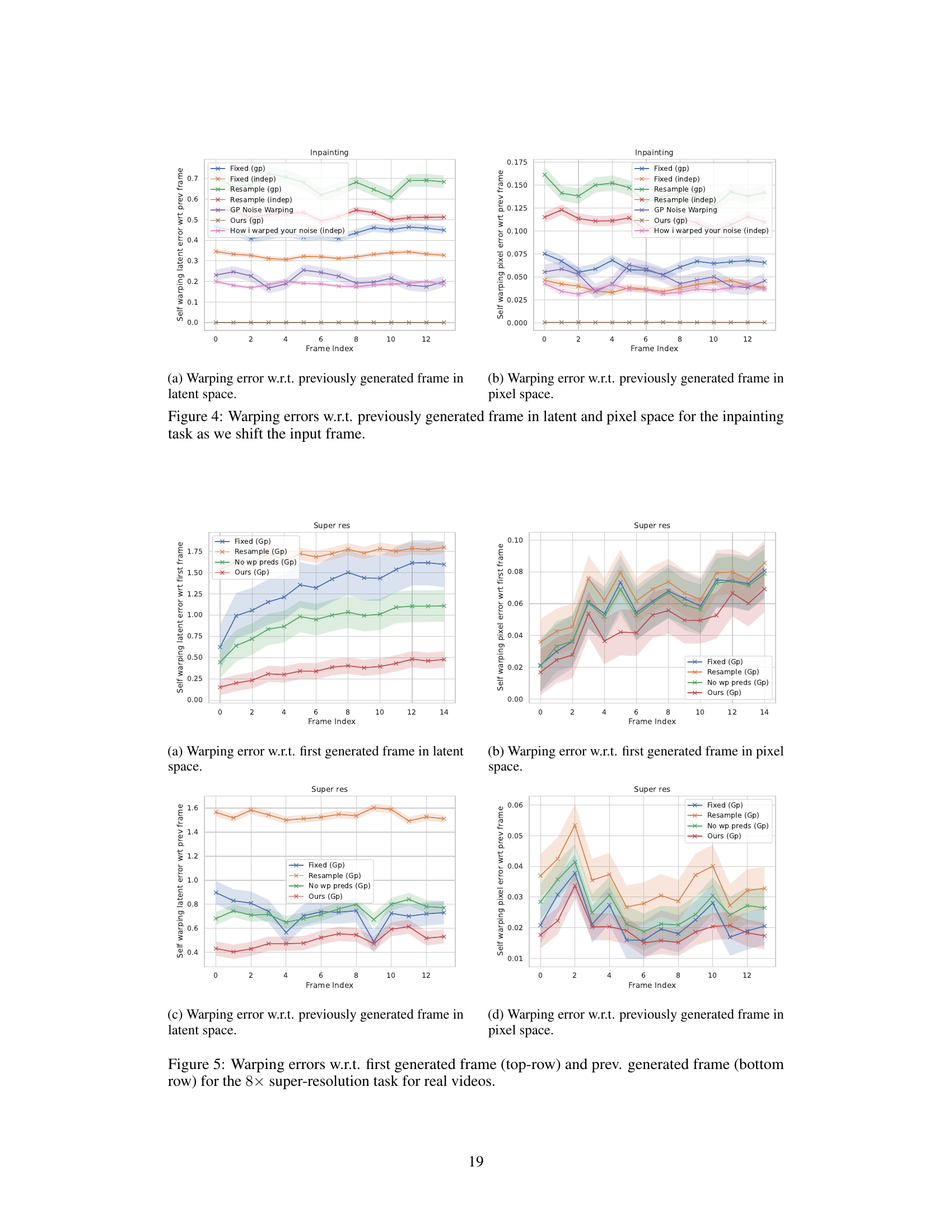
This figure shows the self-warping error, a measure of temporal consistency, for different methods on the inpainting task. The x-axis represents the frame index, and the y-axis represents the self-warping error in both latent space (left) and pixel space (right). The figure shows that the proposed method (Ours (gp)) achieves significantly lower warping error compared to baselines, indicating better temporal consistency.

This figure visualizes the temporal consistency of different methods by showing the self-warping error with respect to the first frame for the inpainting task. The x-axis represents the frame index, and the y-axis represents the self-warping error, which measures how consistent the model’s predictions are across time. Lower values indicate better temporal consistency. The figure compares several methods, including the proposed Warped Diffusion method, and several baselines such as Fixed Noise, Resample Noise, and How I Warped Your Noise.

This figure shows the self-warping error for the inpainting task. The self-warping error measures how consistent the model’s predictions are across time. In this experiment, the input frame is shifted smoothly, and the figure shows the self-warping error in both latent space and pixel space. The results show that Warped Diffusion is the only method that achieves temporal consistency while maintaining high reconstruction performance.

The figure shows the self-warping error for the inpainting task. The self-warping error measures how consistent the model’s predictions are across time. For each frame in a video, the model generates an inpainting result. The self-warping error is calculated by comparing the generated frames and seeing how similar they are after being warped to align with a reference frame (either the first frame or the previous frame). Lower self-warping error indicates better temporal consistency. The x-axis represents the frame index in the video, and the y-axis represents the self-warping error. The plot shows multiple lines, each representing a different method (Fixed noise, Resample noise, How I Warped Your Noise, GP noise warping, and the proposed method). The plot shows that the proposed method (Ours (gp)) significantly outperforms all baselines in terms of temporal consistency.
This figure shows the self-warping error for the inpainting task in both latent and pixel space. The x-axis represents the frame index while the y-axis represents the warping error. Different methods are compared, including ‘Fixed (gp)’, ‘Resample (gp)’, ‘GP Noise Warping’, ‘How I Warped Your Noise (indep)’, and ‘Ours (gp)’. The figure demonstrates how the proposed method (‘Ours (gp)’) significantly outperforms other methods in maintaining temporal consistency across frames.

This figure shows the self-warping error, a measure of temporal consistency, for different methods in video inpainting. The x-axis represents the frame index, while the y-axis represents the self-warping error. Different lines represent different noise warping methods (Fixed, Resample, How I Warped Your Noise, GP Noise Warping, and Ours). The results demonstrate that our method (Ours) significantly outperforms other methods in maintaining temporal consistency across frames, achieving a significantly lower self-warping error.
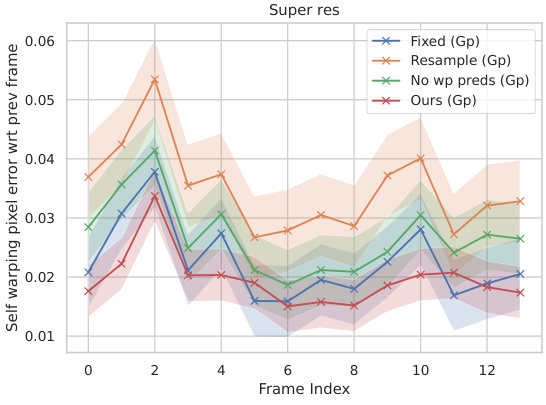
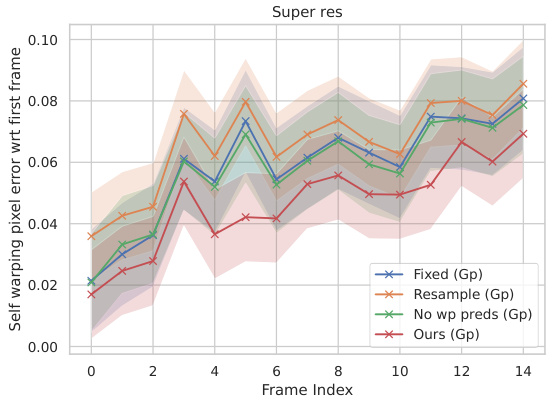
This figure shows the self-warping error for the super-resolution task on real videos. The error is measured in both latent and pixel space, and separately for warping relative to the first frame and relative to the previous frame. The results demonstrate the temporal consistency (or lack thereof) of different methods for handling noise during the super-resolution process of video frames.

The figure visualizes the difference between independent noise and noise sampled from a Gaussian process. The left panel (a) shows a sample of independent noise, exhibiting a high degree of randomness and lack of spatial correlation. In contrast, the right panel (b) displays a noise sample generated from a Gaussian process, characterized by smoother variations and visible spatial correlation. This highlights the key difference in the structure of noise utilized in the proposed Warped Diffusion method, which employs Gaussian processes for its functional noise model to handle interpolation and inpainting tasks within the video generation process.

This figure shows the inpainting results on images from the COYO dataset. The left column shows the input images with randomly masked regions. The right column presents the results of inpainting these masked regions using the authors’ proposed method, which is a fine-tuned Stable Diffusion XL model trained with correlated noise. This visually demonstrates the model’s ability to generate realistic and coherent inpainting results.

This figure shows inpainting results using the proposed Warped Diffusion method. The left column displays images from the COYO dataset with randomly masked regions, simulating missing parts of a video frame. The right column presents the inpainted results generated by the model after fine-tuning with correlated noise. The comparison highlights the model’s ability to reconstruct missing video content in a temporally coherent manner.

This figure shows examples of super-resolution results obtained using the proposed Warped Diffusion method. The left column displays the downsampled input images from the COYO dataset, while the right column presents the corresponding super-resolution outputs generated by the fine-tuned Stable Diffusion XL model trained with correlated noise. The results visually demonstrate the model’s ability to enhance the resolution of low-resolution images while maintaining details and sharpness.

This figure visualizes the Warped Diffusion method applied to video super-resolution. It shows four steps: (a) a function space diffusion model is developed to super-resolve images using Gaussian process samples; (b) optical flow extracts warping transformations between consecutive input frames; (c) these transformations warp the Gaussian process sample from the previous frame; and (d) equivariance self-guidance in the ODE sampler ensures temporal consistency. This illustrates the process of extending an image diffusion model to work effectively on videos.
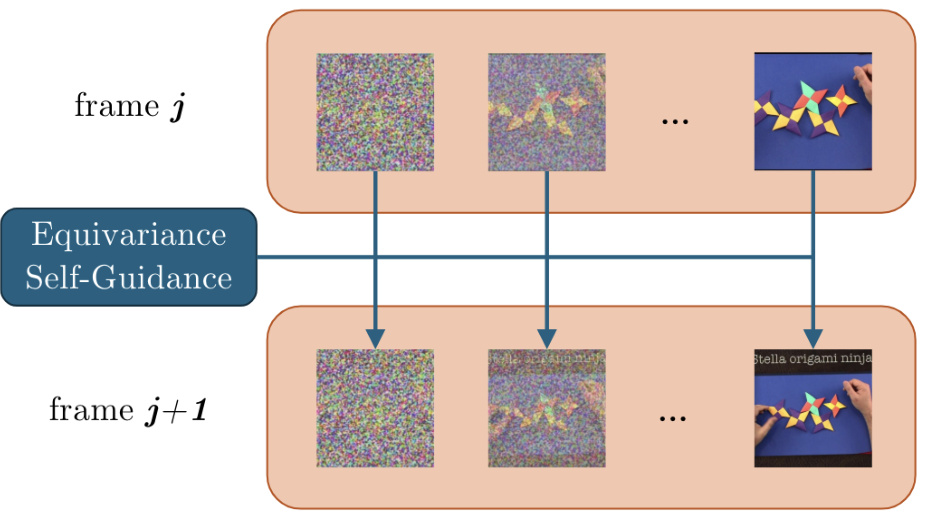
This figure provides a schematic overview of the Equivariance Self-Guidance process used in Algorithm 1. It shows how, for a given frame (frame j), the noise is warped using optical flow, then passed through the diffusion model. The output from this is then used as guidance to ensure that the subsequent frame (frame j+1) maintains temporal consistency. The process is shown for several steps in the sampling chain, to demonstrate how the self-guidance mechanism improves the temporal coherence of the generated video.
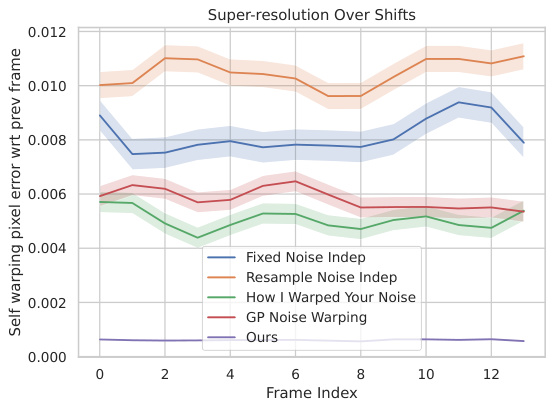
This figure shows the self-warping error over time for the inpainting task. The self-warping error measures the consistency of the model’s predictions across different frames as the input is shifted. Lower values indicate greater temporal consistency. The figure compares several methods, including ‘Fixed Noise’, ‘Resample Noise’, ‘How I Warped Your Noise’, ‘GP Noise Warping’, and the proposed ‘Ours’. The results demonstrate the superior temporal consistency of the proposed ‘Ours’ method.

This figure shows the self-warping error over time for different methods in the inpainting task, where the input frame is shifted at each time step. The ‘self-warping error’ measures the consistency of the model’s output across frames, reflecting the temporal coherence of the generated video. Lower values indicate better temporal consistency. The figure demonstrates that the proposed method (‘Ours’) significantly outperforms the baselines in terms of temporal consistency.
More on tables

This table presents a quantitative comparison of different methods for video inpainting, specifically focusing on the task of frame translation. It shows the average performance across several frames, evaluating the performance of each method with respect to several metrics commonly used for image quality assessment. The metrics include FID, Inception score, CLIP text/image scores, SSIM, LPIPS and MSE. Additionally, it reports a warping error, measuring the temporal consistency of the model’s predictions across frames.
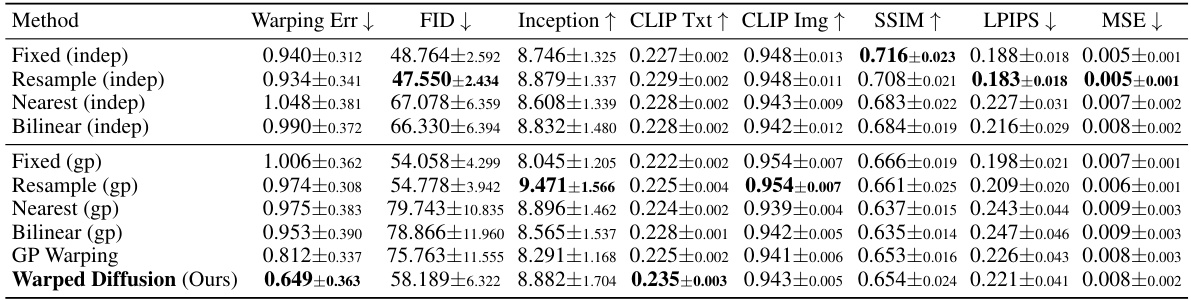
This table presents a quantitative comparison of different super-resolution models on real videos. It evaluates the performance of several methods across various metrics, including FID, Inception Score, CLIP scores (text and image), SSIM, LPIPS, and MSE. The methods are categorized into noise warping baselines and the proposed Warped Diffusion model. The warping error is also included as a measure of temporal consistency. The results highlight the performance gains achieved by Warped Diffusion in terms of both restoration quality and temporal consistency.
Full paper#