↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline imitation learning (IL) aims to train agents by imitating expert demonstrations without online interaction. A common challenge is ‘covariate shift’, where the learned agent’s behavior differs from the expert’s, often leading to poor performance. This is further exacerbated when expert datasets are not collected from a stationary distribution (a stable, long-term behavior). Existing IL methods often struggle in these situations.
This paper introduces DrilDICE, a new method designed to solve this problem. DrilDICE employs a distributionally robust optimization technique, focusing on the stationary distribution. This addresses the covariate shift by using a stationary distribution correction ratio estimation and a distributionally robust BC objective. Extensive experiments demonstrate DrilDICE’s effectiveness in various covariate shift scenarios, significantly outperforming existing offline IL approaches. The results highlight its robustness and ability to handle biased and non-stationary data.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles a critical issue in offline imitation learning (IL): covariate shift. The proposed method, DrilDICE, offers a robust solution that outperforms existing techniques, opening avenues for more reliable and effective offline IL applications. This is particularly important for scenarios with limited interaction with the environment and/or biased datasets. The work also introduces valuable insights into distributionally robust optimization and its applications in IL.
Visual Insights#

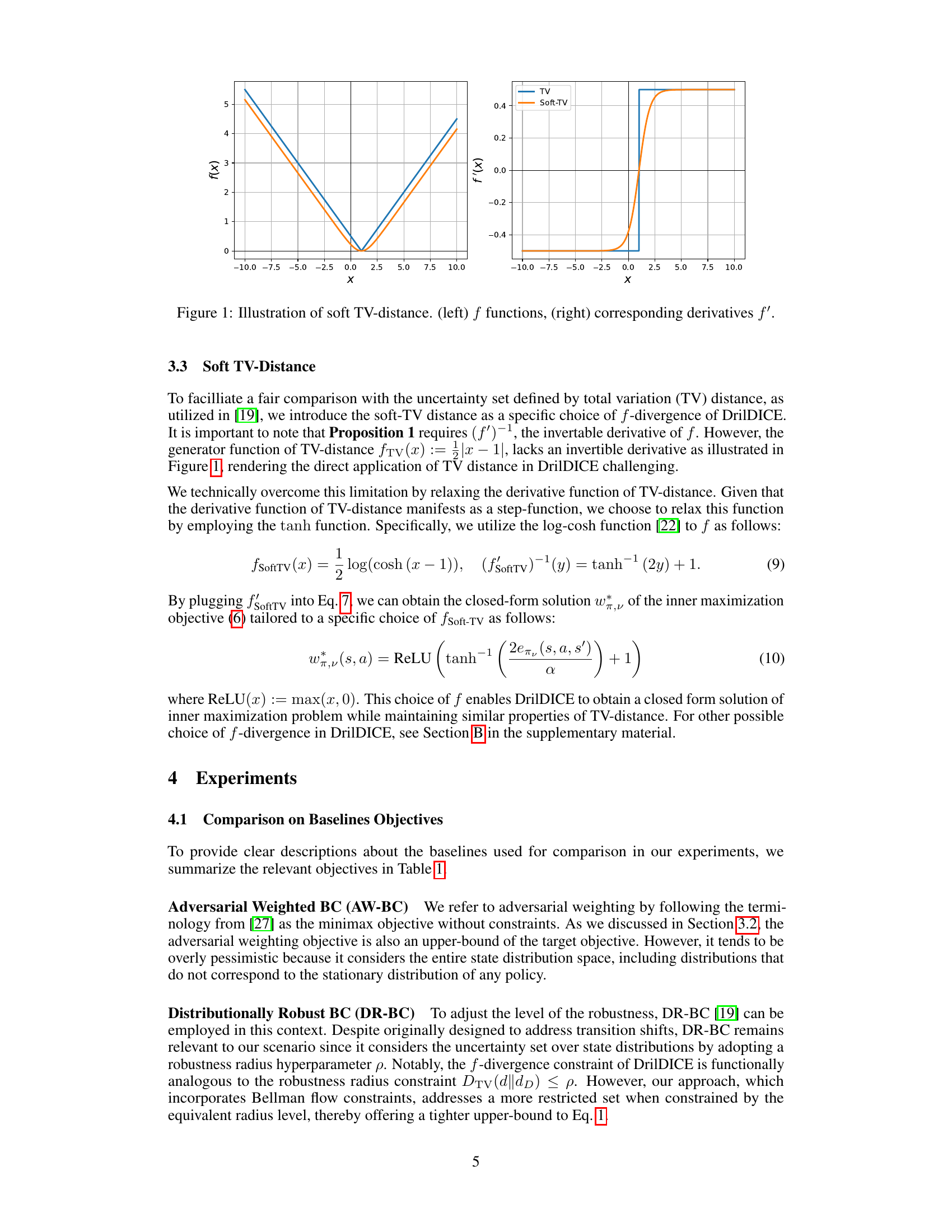
This figure illustrates the soft TV-distance, a modification of the total variation (TV) distance used to address the lack of an invertible derivative in the original TV distance. The left panel shows a comparison of the f functions for the TV distance and the proposed soft TV-distance. The right panel shows a comparison of their corresponding derivatives (f’). The soft TV-distance uses a smooth approximation of the TV distance’s derivative, making it suitable for use in the DrilDICE algorithm.

This table compares the objective functions of several offline imitation learning algorithms. It highlights the differences in how they handle covariate shift, particularly focusing on distribution matching, adversarial weighting, and distributionally robust optimization techniques. The table shows the different objective functions, including those used in baselines (AW-BC, DR-BC) and the proposed approach (Worst-case weighting). It emphasizes the use of a stationary distribution class Q in the objective functions of distributionally robust methods.
In-depth insights#
Robust BC via DICE#
The heading ‘Robust BC via DICE’ suggests a method to improve the robustness of Behavioral Cloning (BC) using the DICE (Distribution-Corrected Importance Estimation) algorithm. Standard BC is known to suffer from covariate shift, where the distribution of states encountered during training differs from that during deployment. DICE aims to correct this by estimating the importance weights of expert trajectories, effectively re-weighting the training data to better match the target distribution. By incorporating DICE, this approach likely addresses the covariate shift problem, making the BC more robust and less prone to performance degradation. The robustness likely comes from DICE’s ability to adjust for the differences in state distribution, leading to a more reliable learned policy. The method’s effectiveness would need to be demonstrated empirically through experiments involving various covariate shift scenarios. This approach is likely particularly useful in offline reinforcement learning settings where online interaction is limited or impossible. Success would significantly improve the reliability and applicability of BC in various real-world problems.
Covariate Shift Issue#
The covariate shift issue in imitation learning is a critical challenge arising from a mismatch between the training data distribution and the distribution encountered during deployment. Behavioral Cloning (BC), a popular offline imitation learning method, is particularly vulnerable. The core problem is that expert demonstrations, used to train the BC model, might not accurately represent the states the agent will encounter when operating under its own learned policy. This leads to poor generalization and a significant performance drop. Addressing this issue often involves techniques like distribution matching, aiming to align the stationary distribution of the learned policy with that of the expert. However, the success of distribution matching depends heavily on the assumption that the expert data is sampled from the expert’s stationary distribution, which is often unrealistic in practice. This limitation highlights the need for more robust approaches that can handle covariate shift even when the training data is not perfectly representative of the deployment environment. Robust solutions often employ distributionally robust optimization, focusing on minimizing the worst-case performance across a range of possible distributions. This is often more computationally demanding but offers greater robustness.
DrilDICE Algorithm#
The DrilDICE algorithm is presented as a novel approach to offline imitation learning, specifically designed to address the challenge of covariate shift. It enhances behavioral cloning by incorporating a distributionally robust optimization framework, focusing on stationary distributions rather than merely matching overall state-action distributions. DrilDICE’s key innovation is its use of a stationary distribution correction ratio estimation (DICE) to derive a feasible solution to the robust optimization problem. This allows it to efficiently learn a policy that is robust to shifts in the data distribution, particularly those caused by biased data collection or incomplete trajectories. The algorithm is shown to outperform baselines in experiments with varied covariate shift scenarios, demonstrating its efficacy in improving robustness and overcoming limitations of traditional distribution-matching approaches. A particularly interesting aspect is the algorithm’s use of soft TV-distance to achieve smooth solutions, allowing for better practical performance. This robustness is crucial in offline imitation learning, where interactions with the environment are unavailable.
Imbalanced Datasets#
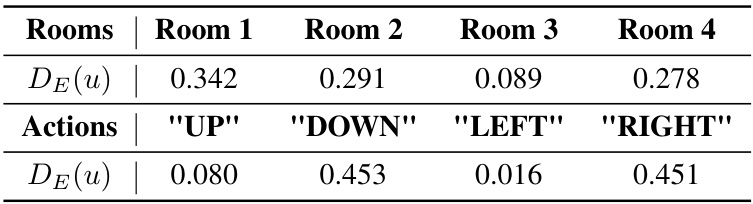
The concept of “Imbalanced Datasets” is crucial in evaluating the robustness of imitation learning models. An imbalanced dataset arises when the distribution of states or actions in the training data does not reflect the real-world distribution. This is common in offline imitation learning due to various factors, such as biased data collection or limited interaction with the environment. In such cases, a model trained on an imbalanced dataset may perform poorly when deployed to a new environment, exhibiting the covariate shift problem. The authors cleverly address this issue by proposing a novel method to mitigate covariate shift. This method focuses on improving the robustness of the model against imbalanced datasets. The core idea is to use a distributionally robust optimization approach, which considers the worst-case scenario within a specific set of possible data distributions. The results demonstrate that the proposed method improves the robustness of the model against covariate shift, especially in scenarios with significantly imbalanced datasets. This highlights the significance of addressing data imbalance in offline imitation learning to achieve real-world applicability and reliable performance.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the DrilDICE framework to handle more complex scenarios, such as those involving noisy expert demonstrations or transitions shifts, would significantly broaden its applicability. Investigating the impact of different divergence choices on the model’s robustness and efficiency is another key area. The development of more efficient optimization techniques for solving the distributionally robust optimization problem would be beneficial, particularly for high-dimensional state spaces. Finally, empirical evaluations on real-world datasets are crucial to demonstrate the practical effectiveness of the approach and compare its performance against existing state-of-the-art methods in real-world settings where covariate shifts frequently occur.
More visual insights#
More on figures
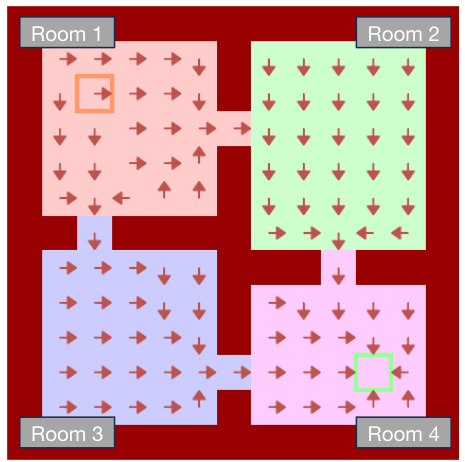
This figure shows the Four Rooms environment used in the experiments. The environment is a grid world with four distinct rooms connected by doorways. The goal is to navigate from a starting location (orange square) to a goal location (green square). The red arrows indicate the path taken by the deterministic expert policy used to collect the expert demonstration dataset.

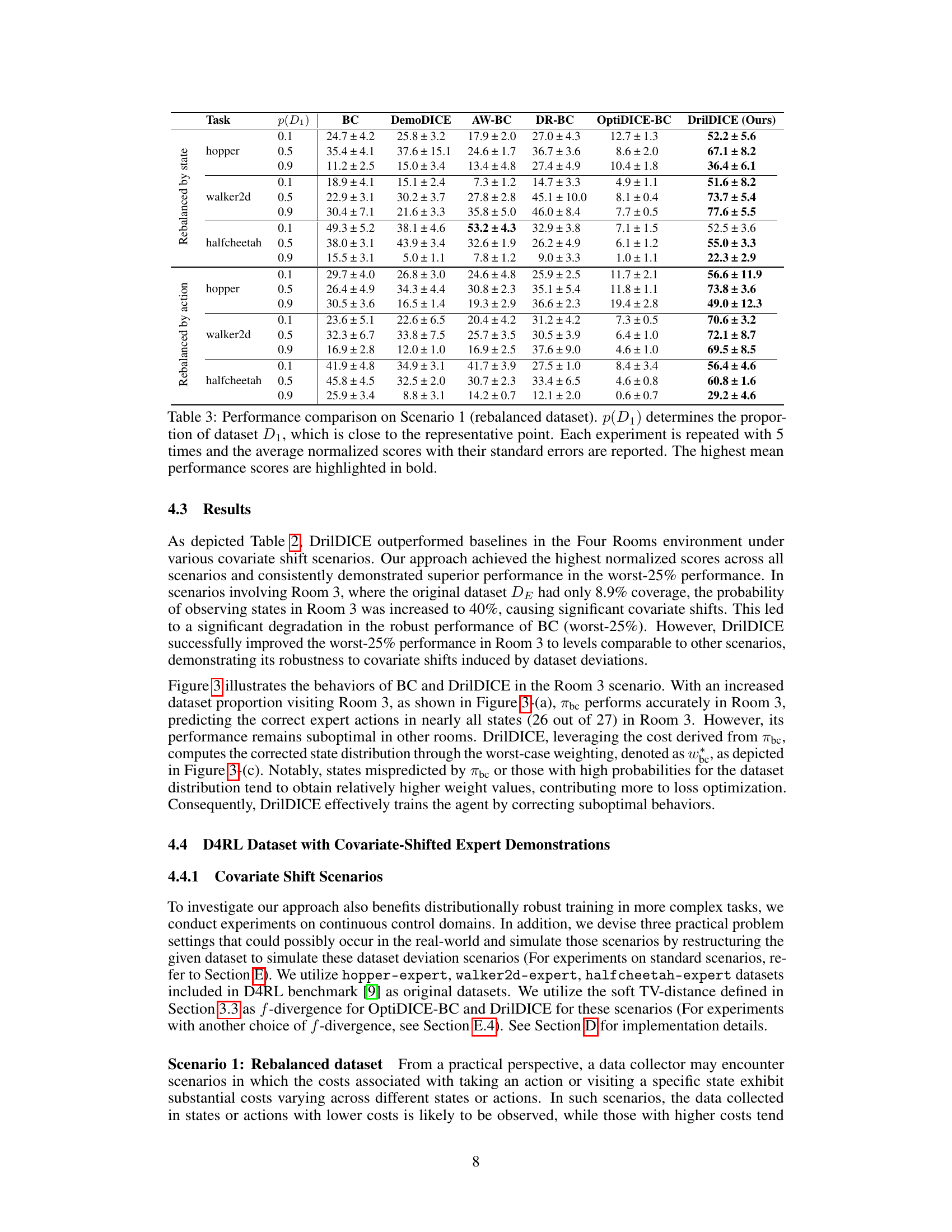
This figure visualizes the state distributions and policy behaviors of different methods in the Four Rooms environment. Panel (a) shows the state distribution of the dataset (dp(s)). Panel (b) shows the state distribution induced by the behavioral cloning (BC) policy (dπE(s)). Panel (c) presents the corrected state distribution (d(s)wbe(s)) obtained by weighting the original dataset distribution using the weights (wbe(s)) derived from the DrilDICE algorithm. Finally, panel (d) shows the state distribution of the DrilDICE policy (dπnew(s)), which is a result of behavioral cloning with the weights from DrilDICE.
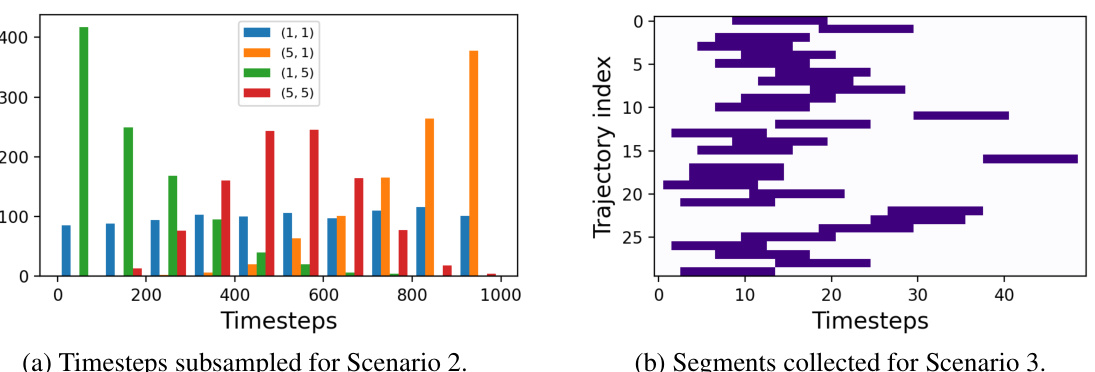
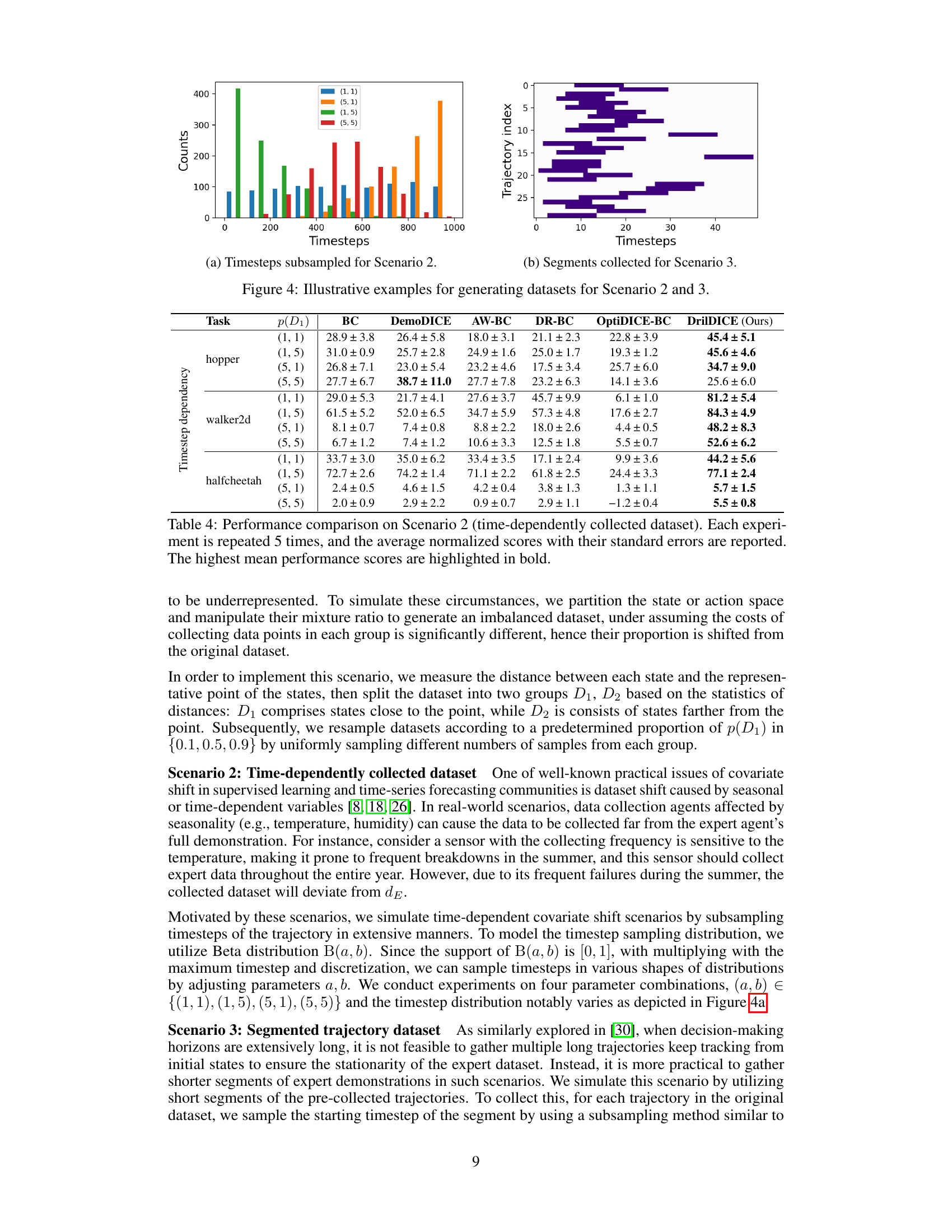
This figure illustrates how datasets are generated for scenarios 2 and 3 in the paper. Scenario 2 simulates time-dependent data collection, where data is collected with varying frequencies at different timesteps. This is shown in subfigure (a) where the x-axis represents timesteps and the y-axis represents the counts of collected data at each timestep, with different colored bars representing different parameter combinations. Scenario 3 simulates segmented trajectory data collection, where only short segments of the trajectories are collected instead of complete trajectories. Subfigure (b) shows this by representing the trajectory indices on the y-axis, and timesteps on the x-axis. The dark purple blocks indicate the segments of trajectories collected for training.
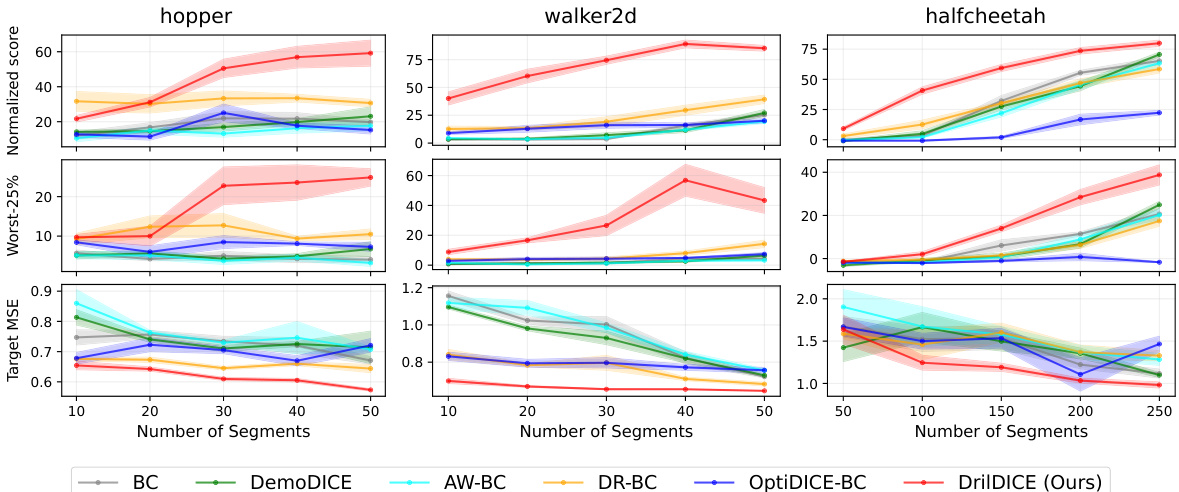
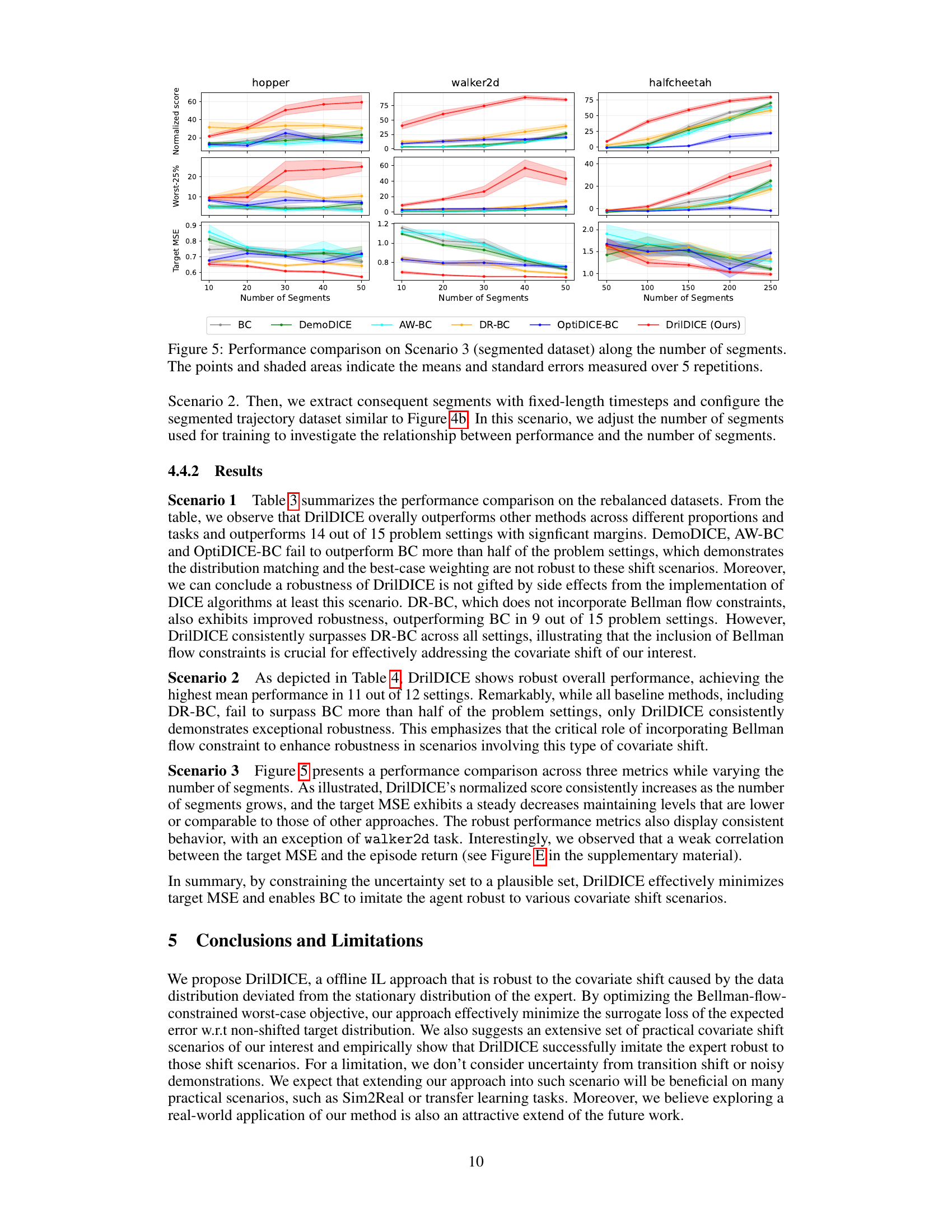
This figure compares the performance of different imitation learning methods (BC, DemoDICE, AW-BC, DR-BC, OptiDICE-BC, and DrilDICE) on the segmented dataset scenario of the D4RL benchmark. The x-axis represents the number of segments used, and the y-axis shows three different metrics: normalized score, worst-25% performance, and target MSE. The shaded areas represent standard errors from 5 repetitions, showing the variability of the results. The figure helps to understand how the performance of each method changes as the length of the trajectories used for training changes. DrilDICE generally shows better performance with more segments.

This figure shows an example MDP with three states (S1, S2, S3) and two actions (a1, a2). The expert policy (πE) and an imitator policy (π^) are defined, along with their corresponding state distributions (dE, dπ). The transition probabilities are deterministic. The figure also illustrates a data distribution (dD1) that differs from the expert’s distribution, highlighting a covariate shift scenario. This example is used to demonstrate how the standard behavioral cloning approach’s loss minimization does not guarantee a reduction in the performance gap between the expert and the imitator.

This figure visualizes the f-divergence functions (left), their derivatives (middle), and the closed-form solution of the inner maximization problem (right). Different f-divergence choices (KL, χ², soft χ², TV, soft TV) are compared. The derivatives are important because they are used to obtain the closed-form solution. The closed-form solution is a crucial part of the DrilDICE algorithm for efficiently solving the optimization problem.

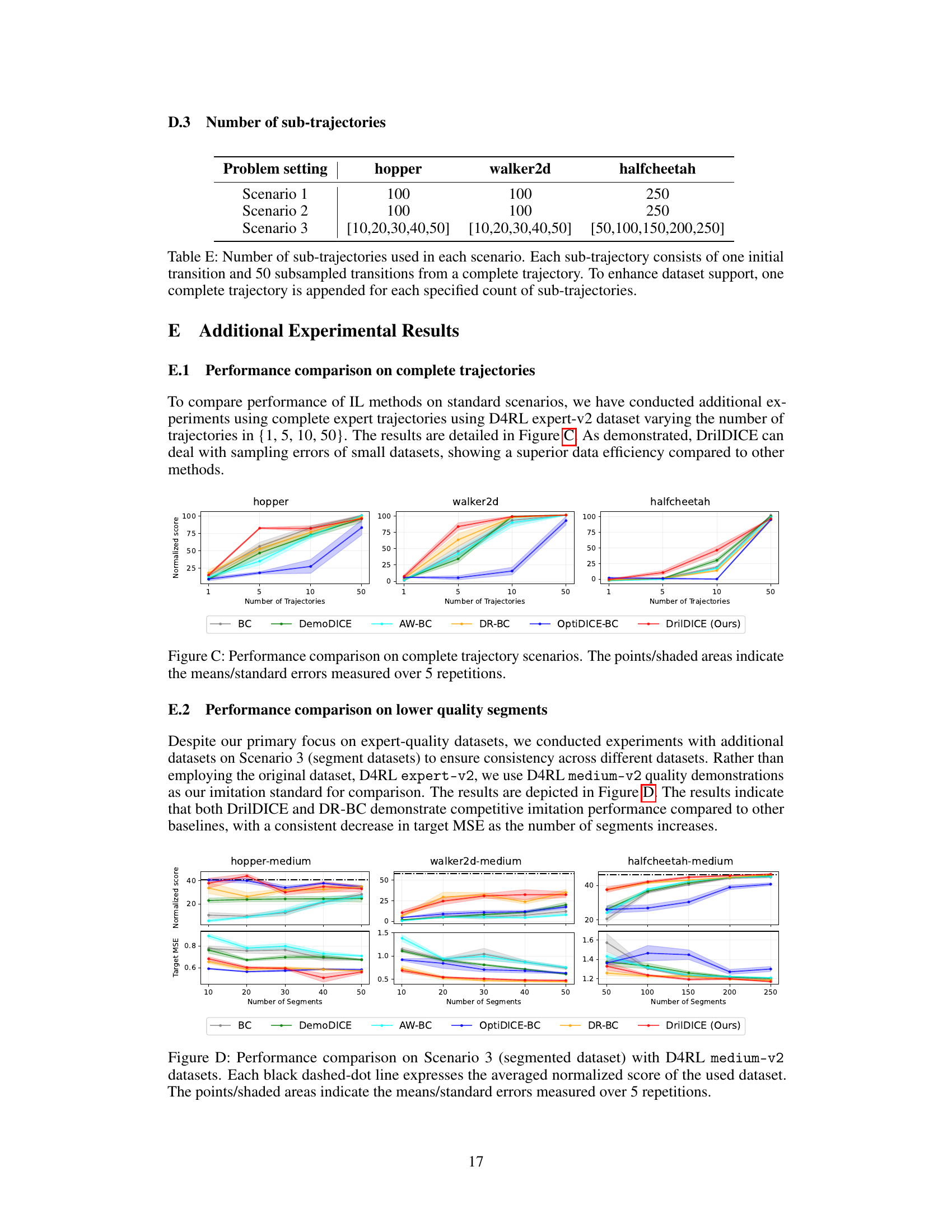
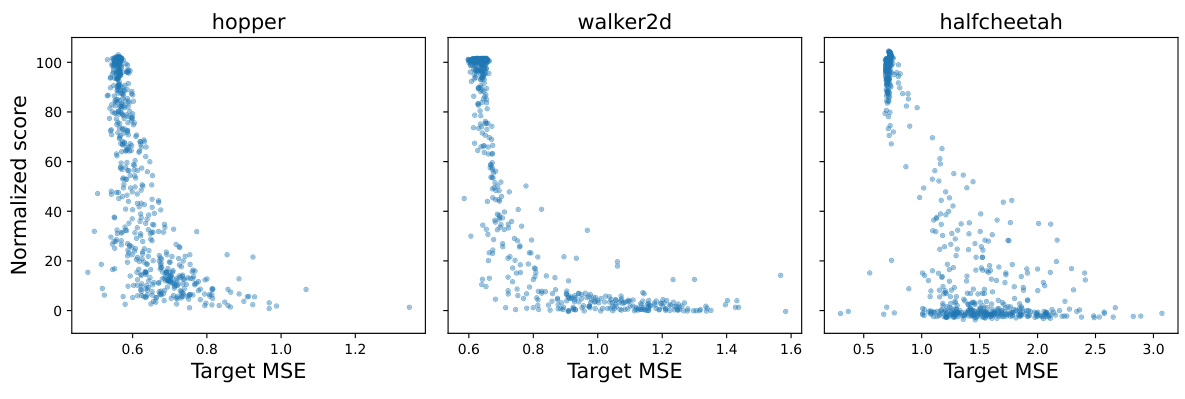
This figure compares the performance of different imitation learning methods (BC, DemoDICE, AW-BC, DR-BC, OptiDICE-BC, and DrilDICE) on complete expert trajectories with varying numbers of trajectories (1, 5, 10, 50). The y-axis represents the normalized score, and the x-axis shows the number of trajectories used in training. The shaded areas represent the standard errors of the mean, indicating the variability in performance across multiple repetitions of the experiment. The results show DrilDICE achieves superior performance and data efficiency compared to other methods, especially with smaller datasets.

This figure compares the performance of different imitation learning methods (BC, DemoDICE, AW-BC, OptiDICE-BC, DR-BC, and DrilDICE) on the segmented dataset in Scenario 3. The x-axis represents the number of segments used in training, and the y-axis shows the normalized score and target MSE. The points represent the average performance over 5 repetitions, and the shaded areas show the standard error. The results demonstrate how the performance of each method changes as the number of segments increases.
This figure compares the performance of different imitation learning methods (BC, DemoDICE, AW-BC, DR-BC, OptiDICE-BC, and DrilDICE) on the segmented dataset scenario of Scenario 3 from the paper. The x-axis represents the number of segments used in training, and the y-axis shows three performance metrics: normalized score, worst-25% performance, and target MSE. The points represent the average performance over 5 repetitions, and the shaded area shows the standard error. The figure demonstrates how the performance of each method changes as the number of segments increases, highlighting the relative effectiveness of DrilDICE across different metrics and dataset conditions.

This figure compares the performance of different algorithms (BC, DR-BC, OptiDICE-BC, and DrilDICE) across three metrics (normalized score, worst-25% performance, and target MSE) as the number of segments in the dataset varies. Each algorithm is tested on three different continuous control tasks (hopper, walker2d, and halfcheetah). The shaded areas represent standard error across 5 repetitions. The results show that DrilDICE consistently outperforms other methods in terms of overall performance and robustness, particularly when the number of segments is low.
More on tables
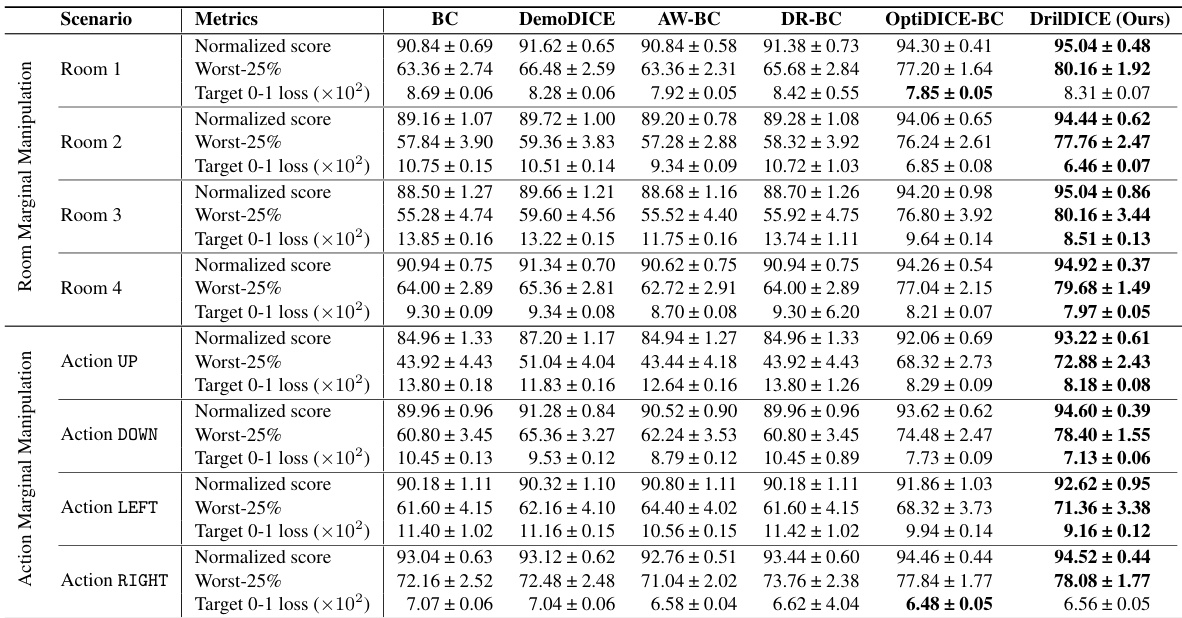
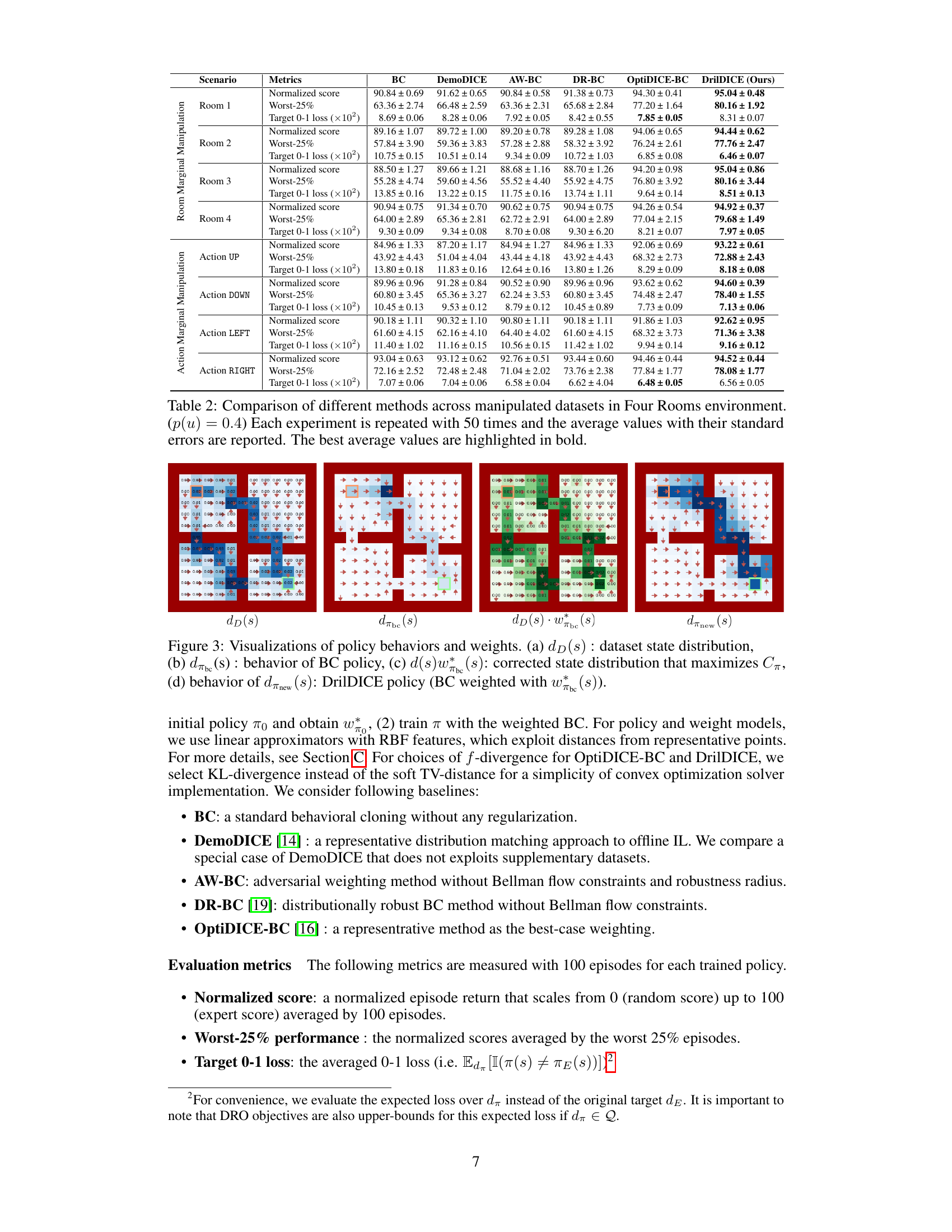
This table presents a comparison of different imitation learning methods across various scenarios with manipulated datasets in the Four Rooms environment. The manipulation involves adjusting the probability of specific rooms or actions in the dataset to simulate covariate shift. Each method’s performance is evaluated using three metrics: Normalized score, Worst-25% performance, and Target 0-1 loss. The results are averaged over 50 repetitions and include standard errors. The best performing method in each scenario is highlighted in bold.

This table presents a comparison of different imitation learning methods across various scenarios in the Four Rooms environment. The scenarios involve manipulating the dataset to simulate covariate shift by changing the marginal distribution of rooms or actions. The table shows the normalized score, worst-case 25% performance (the average score of the worst 25% episodes), and the target 0-1 loss for each method and scenario. The best average value for each metric is highlighted in bold.
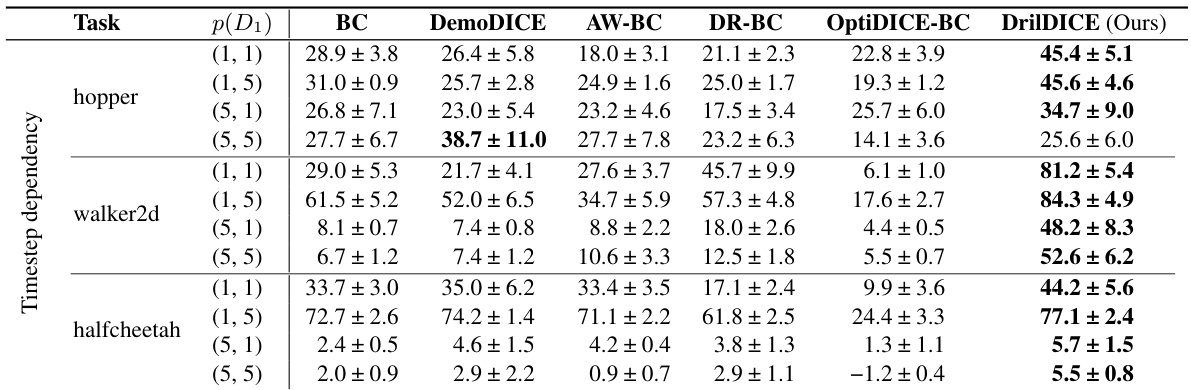
This table presents the results of experiments conducted under the time-dependent data collection scenario in Scenario 2. The table shows the performance comparison of different offline imitation learning methods across three different tasks (hopper, walker2d, and halfcheetah). Each task is evaluated with different state distributions, represented by the parameter p(D1), and different numbers of time steps included in data samples (1,1), (1,5), (5,1), and (5,5). The results are given as the average normalized score (mean ± standard error) over 5 repetitions. The method with the best average score for each scenario is highlighted in bold.

This table summarizes the objective functions of various offline imitation learning approaches, including distribution matching, adversarial weighted behavioral cloning (AW-BC), distributionally robust behavioral cloning (DR-BC), best-case weighting, and the proposed worst-case weighting. It highlights the differences in how these methods handle covariate shift and the stationary distribution of policies.
This table compares the objective functions of different offline imitation learning methods. It shows the objective function for distribution matching, adversarial weighted BC (AW-BC), distributionally robust BC (DR-BC), best-case weighting, and the proposed worst-case weighting method. The table highlights the differences in how these methods address the covariate shift problem in behavioral cloning, particularly focusing on the stationary distribution and robustness to distribution shifts.

This table summarizes the hyperparameters used in the D4RL benchmark experiments for different algorithms: BC, DemoDICE, AW-BC, DR-BC, OptiDICE-BC, and DrilDICE. It includes the policy distribution, batch size, policy learning rate, hidden units, training iterations, and learning rates for the additional parameters (alpha, rho, nu/w). Note that some hyperparameters varied across multiple values; these are shown within brackets.

This table shows the number of sub-trajectories used in each scenario of the experiments. Each sub-trajectory consists of an initial transition and 50 subsampled transitions. To ensure sufficient data, a complete trajectory is added to each sub-trajectory count.

This table presents a comparison of the performance of several algorithms on a Four Rooms environment with imbalanced datasets. The algorithms are compared based on three metrics: Normalized score, Worst-25% performance, and Target 0-1 loss. The table is organized by the type of data manipulation (Room Marginal Manipulation and Action Marginal Manipulation). Each manipulation is tested with a probability of 0.4, and the results show that DrilDICE consistently outperforms other methods across various scenarios.
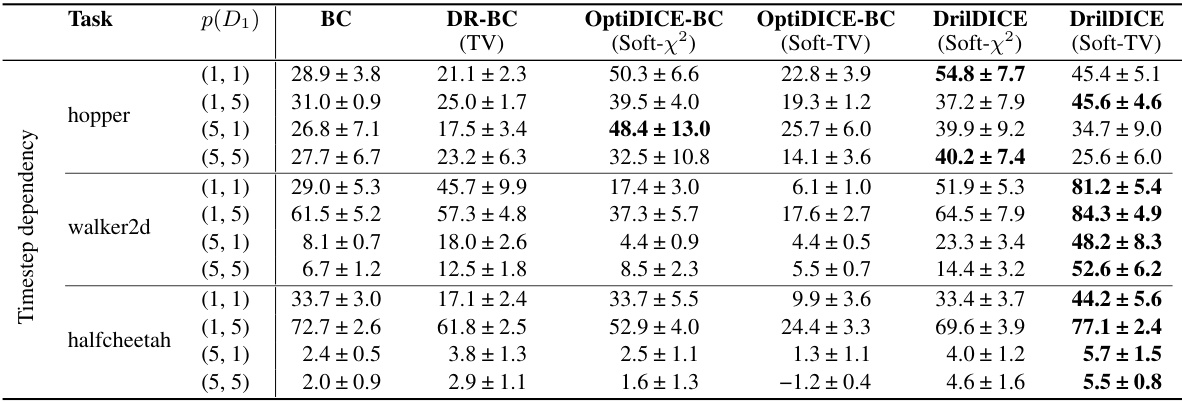
This table presents the performance comparison of different imitation learning methods on Scenario 2, which involves time-dependent data collection. The results show the normalized scores (with standard errors) for different tasks (hopper, walker2d, halfcheetah) and various proportions of dataset D1 (representing the time-dependent data). The best-performing method for each setting is highlighted in bold.
Full paper#