TL;DR#
Large language models rely heavily on transformers, whose core mechanism, self-attention, suffers from a critical issue: rank collapse, meaning model representations become homogeneous as the model’s depth increases. This phenomenon limits the expressivity and potential of deep models. Previous research mostly overlooked the role of other transformer components like attention masks and LayerNorm in addressing this.
This paper presents a rigorous analysis of rank collapse under self-attention, considering the impact of both attention masks and LayerNorm. The researchers found that while masked self-attention still exhibits rank collapse, sparse or local attention can slow down the collapse rate. Furthermore, they refuted the widely held belief that LayerNorm plays no role in rank collapse. Their experiments revealed that with LayerNorm and careful selection of value matrices, the self-attention dynamics can sustain a diverse set of equilibria (states) with varying ranks, actively avoiding complete collapse to a low-rank solution for a wide range of input sequences.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges existing assumptions about the role of LayerNorm in transformers and provides a more nuanced understanding of the self-attention dynamics. It reveals LayerNorm’s capability to prevent rank collapse, a critical issue that limits model expressivity. The findings open avenues for designing more expressive and versatile transformer architectures and improving the performance of existing models. This work is highly relevant to researchers working on the theoretical foundations of transformers, large language models, and improving the efficiency of existing models.
Visual Insights#

🔼 This figure illustrates the long-term behavior of two tokens (N=2) in a two-dimensional space (d=2) under self-attention dynamics, with and without Layer Normalization (LayerNorm). The left panel shows that without LayerNorm, both tokens collapse to the same point, indicating rank collapse. In contrast, the right panel demonstrates that with LayerNorm, the tokens can maintain full rank and converge to different points. The behavior with LayerNorm depends on the initial positions of the tokens; the second token will converge to either point A or point B depending on its initial location in the plane.
read the caption
Figure 1: Long-term behavior of tokens in the case of N = 2, d = 2. Without LayerNorm (left), both tokens collapse to the same point in R2; whereas with LayerNorm (right), such a collapse would not necessarily happen and token representations can maintain full rank in the long term (first token converges either to (0, 1) or (0, -1). Assuming convergence to (0, 1) for the first token, the second token converges to B, if it is initially located within the red segment).
In-depth insights#
Attn Mask Effects#
The effects of attention masks on the behavior of transformer models are multifaceted and significant. Studies show that fully bidirectional attention, without masking, leads to exponential rank collapse, where token representations converge to a homogeneous state, limiting model expressivity as depth increases. However, the introduction of attention masks, particularly causal or sparse masks, can mitigate this collapse. Causal masking, where tokens only attend to preceding tokens, demonstrably slows down the rate of rank collapse. Sparse attention mechanisms further limit the connections between tokens, resulting in even more controlled dynamics and potentially preventing oversmoothing. The choice of masking strategy thus presents a crucial design consideration, affecting not only computational efficiency but also the model’s ability to capture and maintain the richness of information in input sequences. Further research should investigate the optimal balance between expressivity and efficiency offered by different attention mask designs, which is crucial for advancing the capabilities of larger transformer models.
LayerNorm’s Role#
The role of LayerNorm in Transformers, specifically concerning its impact on the self-attention mechanism and the issue of rank collapse, is a complex and nuanced topic. While previous hypotheses suggested LayerNorm played a negligible role, this paper challenges that assumption. The authors demonstrate that, contrary to earlier findings, LayerNorm’s influence is significant and not easily characterized. In cases with orthogonal value matrices, LayerNorm can still contribute to the exponential convergence of token representations to a common point. However, the paper’s crucial contribution lies in showcasing that with appropriate value matrices, LayerNorm allows for a richer equilibrium landscape, preventing complete rank collapse and enabling a wider range of possible ranks. This means that the self-attention dynamics with LayerNorm are far more expressive and versatile than previously thought, which is of paramount theoretical and practical importance for the development of powerful deep learning models. The discrete-time dynamical system analysis employed in this research also contrasts with previous continuous-time approaches, offering a closer representation of the actual transformer architecture.
Rank Collapse Rate#
The concept of ‘Rank Collapse Rate’ in the context of transformer models refers to the speed at which the representational capacity of the model diminishes as the number of layers increases. A high rank collapse rate indicates a rapid loss of expressiveness, meaning that deeper networks do not necessarily lead to improved performance. This phenomenon is detrimental because it limits the model’s ability to capture complex relationships and nuances in the data. Several factors contribute to the rank collapse rate, including the nature of the attention mechanism itself, the type of attention masking employed (e.g., causal vs. bidirectional), and the presence or absence of normalization techniques such as LayerNorm. Understanding and mitigating the rank collapse rate is crucial for designing efficient and powerful transformer-based models. Strategies to reduce the rank collapse rate include incorporating sparse or local attention mechanisms and carefully considering the role of LayerNorm. While LayerNorm’s impact is complex and not fully understood, this research suggests that it has a more significant role than previously believed in maintaining the expressiveness of deep self-attention.
Equilibria Diversity#
The concept of ‘Equilibria Diversity’ in the context of a research paper likely refers to the variety of stable states or outcomes a system can reach. In the specific case of attention mechanisms within transformers, this would relate to the range of possible final token representations after multiple layers of processing. A high diversity of equilibria implies a richer representational capacity; the network is not confined to a few dominant states. Low diversity, conversely, suggests a system susceptible to oversmoothing or rank collapse, limiting the expressiveness and capacity for capturing complex information. Exploring equilibria diversity involves analyzing the effects of architectural elements such as attention masks, LayerNorm, and value matrix choices on the self-attention dynamics. Understanding how these factors affect the equilibrium landscape is crucial for designing powerful transformers. The ideal scenario is a system capable of reaching a wide array of stable equilibria, allowing it to capture nuanced and multifaceted data representations effectively. A theoretical analysis might quantify the number and types of equilibria, linking these metrics to the network’s capabilities. Empirical investigation would involve testing the system’s behavior on different datasets and tasks, looking for evidence of a rich equilibrium space or signs of restricted dynamics.
Future Directions#
Future research could explore the impact of different attention mask designs on mitigating rank collapse, going beyond the causal and local masks analyzed. Investigating the interaction between LayerNorm and other normalization techniques, such as weight normalization, could reveal further insights into their combined effects on self-attention dynamics. A deeper theoretical investigation is needed to fully understand the role of LayerNorm in preventing collapse under more general conditions and value matrix properties, extending beyond orthogonal matrices. Exploring the connections between the anisotropy of token representations and the expressiveness of the self-attention model with LayerNorm warrants further study. Finally, empirical studies could focus on developing more robust methods for training deep transformer models, incorporating insights from the theoretical findings to address the rank collapse phenomenon more effectively. This may involve new training techniques, architectural modifications, or regularizations that target the specific challenges uncovered by this work.
More visual insights#
More on figures

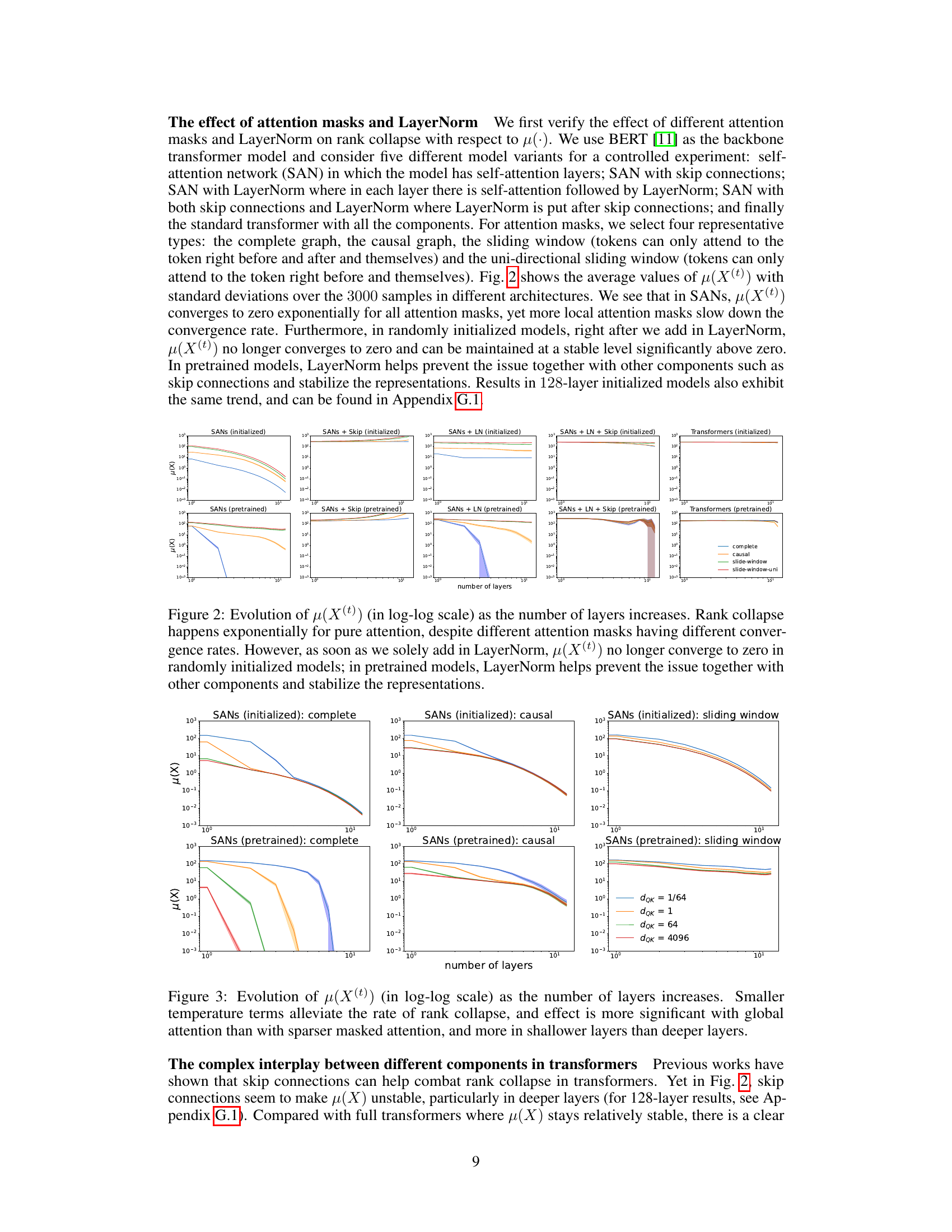
🔼 This figure displays the evolution of token similarity (μ(X(t))) over an increasing number of layers for different transformer architectures. It illustrates the effects of attention masks (complete, causal, sliding window, uni-directional sliding window) and LayerNorm on rank collapse. The results show that without LayerNorm, rank collapse happens exponentially regardless of the attention mask, although local attention masks slow the rate. With LayerNorm, however, the token similarity stabilizes and does not converge to zero, especially in pretrained models where LayerNorm works synergistically with other components to prevent collapse.
read the caption
Figure 2. Evolution of μ(X(t)) (in log-log scale) as the number of layers increases. Rank collapse happens exponentially for pure attention, despite different attention masks having different convergence rates. However, as soon as we solely add in LayerNorm, μ(X(t)) no longer converge to zero in randomly initialized models; in pretrained models, LayerNorm helps prevent the issue together with other components and stabilize the representations.
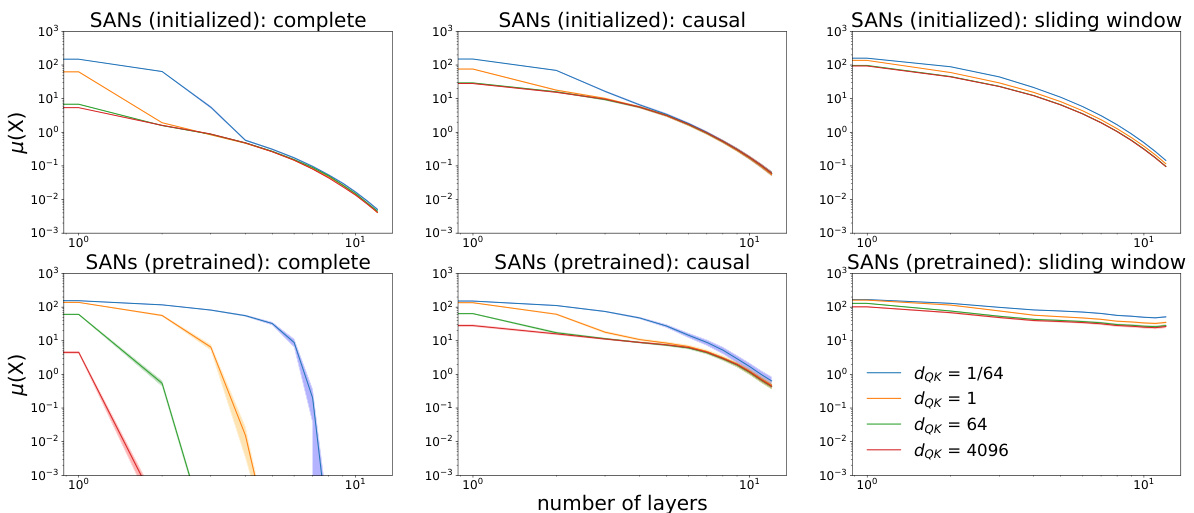
🔼 This figure displays the evolution of the token similarity measure μ(X) as the number of layers increases for different attention masks and temperature terms (dQK). The results show that smaller temperature terms slow down the rate of rank collapse, especially with global attention masks and in earlier layers. This suggests a complex interplay between masking and temperature in controlling the rank collapse phenomenon.
read the caption
Figure 3. Evolution of μ(X(t)) (in log-log scale) as the number of layers increases. Smaller temperature terms alleviate the rate of rank collapse, and effect is more significant with global attention than with sparser masked attention, and more in shallower layers than deeper layers.

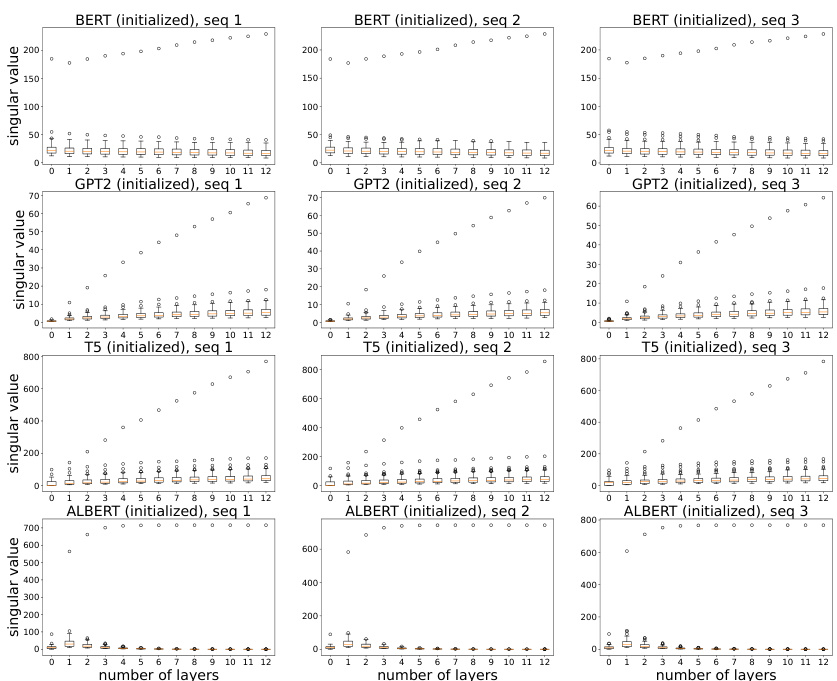
🔼 This figure shows the evolution of token geometry as the number of layers increases in pretrained transformer models. It displays three key metrics: the percentage of full rank, the minimum singular value, and the average absolute cosine similarity between tokens. The results reveal that the models effectively maintain full rank (close to 100%), showcasing the ability of LayerNorm to prevent rank collapse. However, the minimum singular value decreases with depth, and the average absolute cosine similarity increases, indicating an anisotropic representation where tokens cluster in a narrow region, aligning with empirical observations of token embeddings generated by transformers.
read the caption
Figure 4: Evolution of token geometry as the number of layers increases. We see that tokens are indeed able to maintain full rank, while at the same time the representations are anisotropic, meaning that they concentrate in a narrow region, as indicated by the average pairwise absolute cosine similarities.

🔼 This figure shows a comparison of token behavior in a two-token (N=2), two-dimensional embedding space (d=2) scenario with and without LayerNorm. The left panel illustrates that without LayerNorm, both tokens converge to the same point, resulting in rank collapse. The right panel demonstrates that LayerNorm prevents this collapse; even though one token converges to a fixed point, the other token’s position depends on its initial location, potentially maintaining full rank in the long term.
read the caption
Figure 1: Long-term behavior of tokens in the case of N = 2, d = 2. Without LayerNorm (left), both tokens collapse to the same point in R2; whereas with LayerNorm (right), such a collapse would not necessarily happen and token representations can maintain full rank in the long term (first token converges either to (0, 1) or (0, -1). Assuming convergence to (0, 1) for the first token, the second token converges to B, if it is initially located within the red segment).
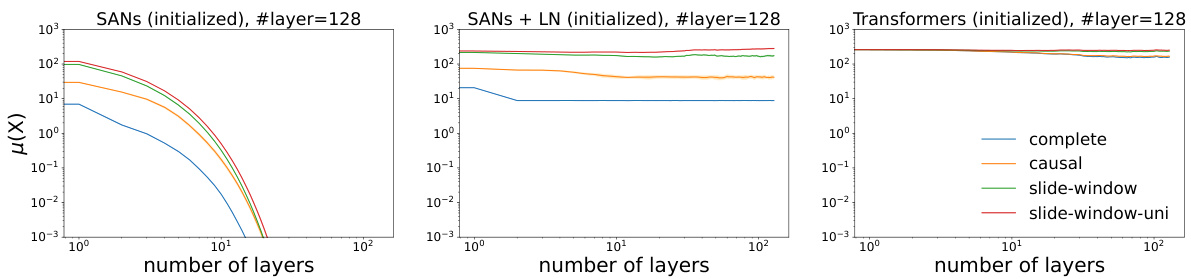
🔼 The figure shows the evolution of the token similarity measure μ(X(t)) as the number of layers increases for different transformer model variants. The results demonstrate an exponential rank collapse in models using only self-attention, even with different attention masks (complete, causal, sliding window, and unidirectional sliding window). The addition of LayerNorm significantly changes the dynamics, preventing the convergence of μ(X(t)) to zero in randomly initialized models. In pre-trained models, LayerNorm, in conjunction with other components, helps prevent rank collapse and stabilizes the token representations.
read the caption
Figure 2. Evolution of μ(X(t)) (in log-log scale) as the number of layers increases. Rank collapse happens exponentially for pure attention, despite different attention masks having different convergence rates. However, as soon as we solely add in LayerNorm, μ(X(t)) no longer converge to zero in randomly initialized models; in pretrained models, LayerNorm helps prevent the issue together with other components and stabilize the representations.
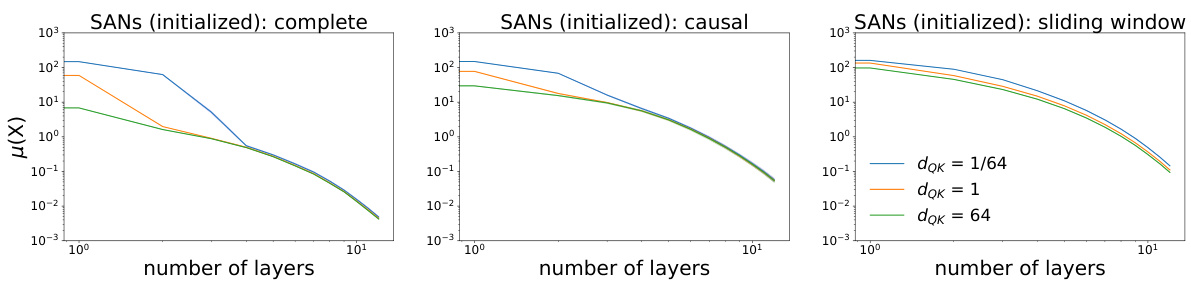
🔼 This figure shows how the token similarity metric μ(X(t)) changes as the number of layers increases for different attention mask types (complete, causal, sliding window) and temperature terms (dQK = 1/64, 1, 64). The results indicate that smaller temperature terms and sparser attention masks lead to slower rank collapse, highlighting the complex interplay between these factors in determining the long-term behavior of transformers.
read the caption
Figure 3. Evolution of μ(X(t)) (in log-log scale) as the number of layers increases. Smaller temperature terms alleviate the rate of rank collapse, and effect is more significant with global attention than with sparser masked attention, and more in shallower layers than deeper layers.
🔼 This figure illustrates the long-term behavior of two tokens (N=2) in a two-dimensional space (d=2) under self-attention dynamics with and without LayerNorm. The left panel shows that without LayerNorm, both tokens collapse to a single point, indicating rank collapse. In contrast, the right panel shows that with LayerNorm, the tokens do not necessarily collapse. The first token converges to either (0,1) or (0,-1), and the position of the second token depends on its initial location.
read the caption
Figure 1: Long-term behavior of tokens in the case of N = 2, d = 2. Without LayerNorm (left), both tokens collapse to the same point in R2; whereas with LayerNorm (right), such a collapse would not necessarily happen and token representations can maintain full rank in the long term (first token converges either to (0, 1) or (0, -1). Assuming convergence to (0, 1) for the first token, the second token converges to B, if it is initially located within the red segment).

🔼 This figure illustrates the long-term behavior of two tokens (N=2) in a two-dimensional space (d=2) under self-attention dynamics with and without LayerNorm. The left panel shows that without LayerNorm, both tokens converge to the same point, indicating rank collapse. The right panel, however, demonstrates that with LayerNorm, rank collapse does not necessarily occur. The tokens can maintain full rank, converging to distinct points depending on their initial positions. The red segment highlights the region of initial positions for the second token that would lead to convergence to point B, given that the first token converges to (0,1).
read the caption
Figure 1: Long-term behavior of tokens in the case of N = 2, d = 2. Without LayerNorm (left), both tokens collapse to the same point in R2; whereas with LayerNorm (right), such a collapse would not necessarily happen and token representations can maintain full rank in the long term (first token converges either to (0, 1) or (0, -1). Assuming convergence to (0, 1) for the first token, the second token converges to B, if it is initially located within the red segment).
Full paper#