↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph learning methods for cognitive diagnosis (CD) suffer from implicit, unified graph representations, leading to poor robustness against noisy student interaction data and underutilization of lower-order exercise latent representations. This paper proposes DisenGCD, a meta multigraph-assisted disentangled graph learning framework.
DisenGCD addresses these issues by disentangling the learning process into three separate graphs: student-exercise-concept interaction, exercise-concept relation, and concept dependency. A meta multigraph module enables effective access to lower-order exercise representations for enhanced student representation learning. The proposed diagnostic function handles three disentangled representations. Experiments demonstrate DisenGCD’s superior performance and robustness compared to existing CD methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in educational data mining and cognitive diagnosis. It introduces a novel framework that significantly improves the robustness and accuracy of student knowledge assessment. The proposed meta multigraph learning approach is highly innovative and opens exciting avenues for further research in disentangled graph representation learning and intelligent tutoring systems. The findings directly impact the development of more effective and robust educational technologies.
Visual Insights#
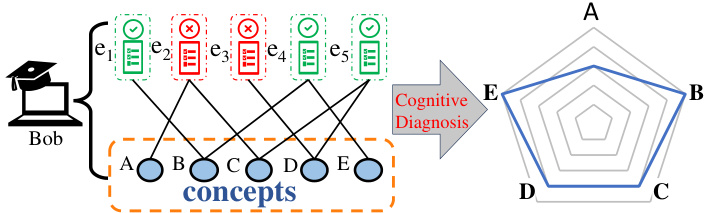
This figure illustrates the core concept of cognitive diagnosis (CD). Student Bob’s responses to five exercises (e1 to e5) are shown, along with indicators of whether the response was correct (green checkmark) or incorrect (red X). These exercises are connected to underlying concepts (A to E), representing the knowledge areas assessed by the exercises. The CD process takes these responses and exercise-concept relations as input to generate a student’s mastery profile, which is visualized as a radar chart showing Bob’s proficiency in each concept.

This table presents the number of students, exercises, concepts, and total logs for three datasets used in the paper’s experiments: ASSISTments, Math, and SLP. It also shows the average number of logs per student in each dataset. This information is crucial for understanding the scale and characteristics of the data used to evaluate the proposed model and compare it against other state-of-the-art methods.
In-depth insights#
Disentangled Learning#
Disentangled learning aims to learn independent representations for different factors of variation within data. In the context of the provided research paper, this likely involves separating the influence of student interactions from the inherent properties of exercises and concepts. This disentanglement is crucial because the student’s responses are noisy and may not accurately reflect their true understanding of the concepts. By isolating concept and exercise representations from the noisy interaction data, the model gains robustness and can better predict student mastery even with imperfect response data. The success of disentangled learning hinges on effectively decomposing complex relationships into meaningful, independent factors, allowing for a more accurate and interpretable representation of student knowledge. This approach is especially important when dealing with educational data, which is often noisy and heterogeneous.
Meta Multigraph Module#
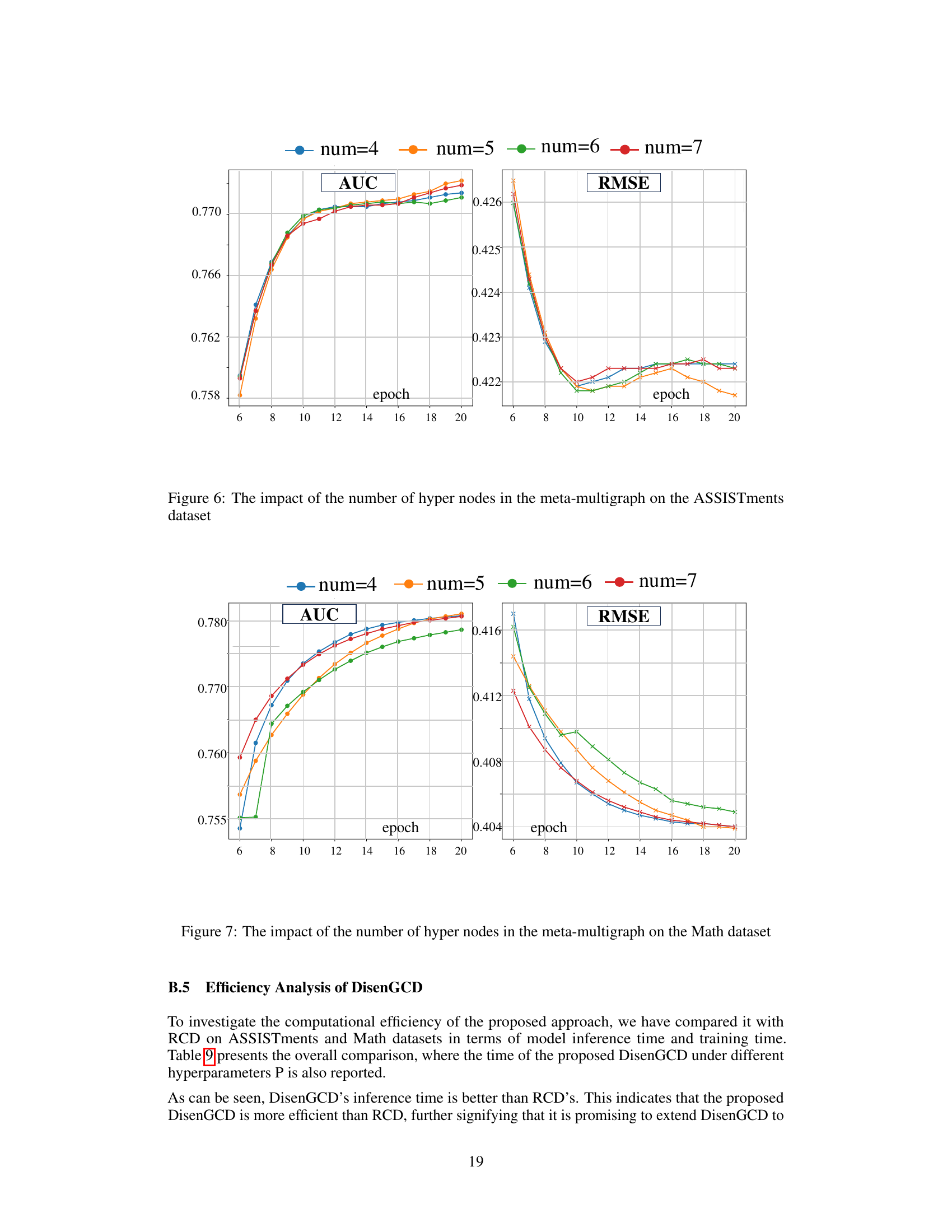
The Meta Multigraph Module is a crucial innovation designed to enhance the robustness and effectiveness of student representation learning within the DisenGCD framework. By creating multiple learnable propagation paths, it allows the current student latent representation to access and integrate information from lower-order exercise latent representations, leading to more comprehensive and robust student profiles. This multi-path architecture is a significant departure from traditional graph neural networks which typically follow single propagation paths. The module’s ability to incorporate lower-order information helps mitigate the negative impact of noise in student interactions, a problem that plagues many existing cognitive diagnosis models. The meta-multigraph structure itself is learned, implying that the model dynamically adapts to the data, ensuring optimal information flow for each student. This adaptive capability is a key strength, allowing DisenGCD to perform well on diverse datasets and handle variations in student response patterns. The success of this module underscores the potential of meta-graph learning for improving the accuracy and reliability of cognitive diagnosis.
Robustness Analysis#
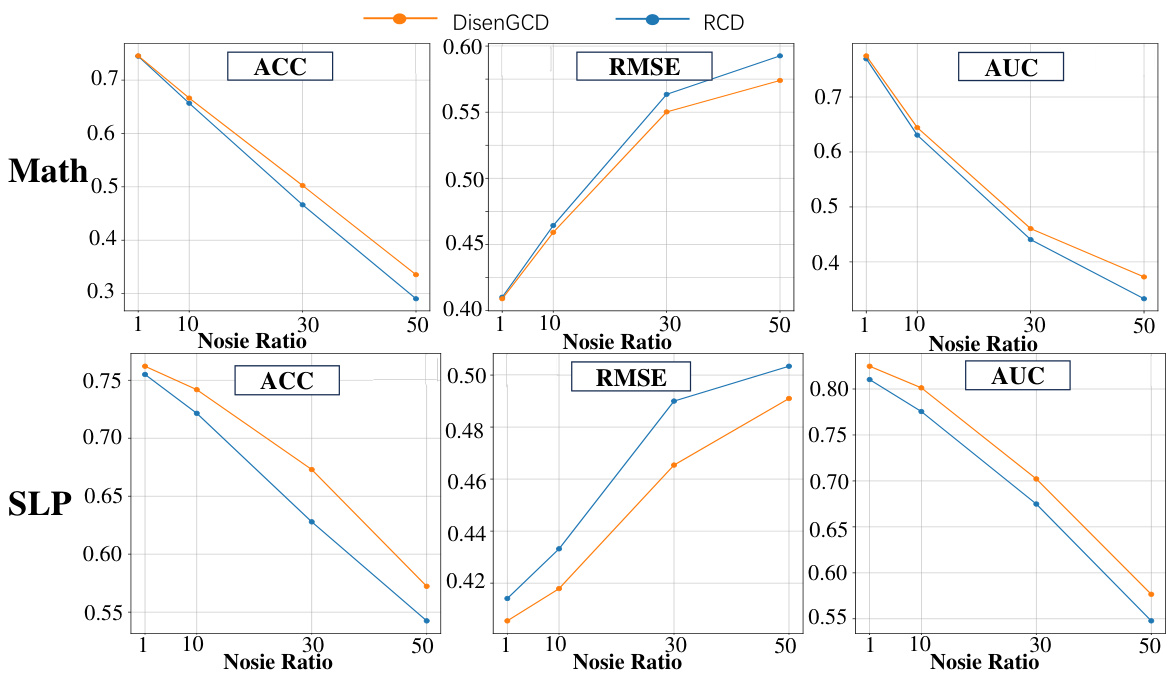
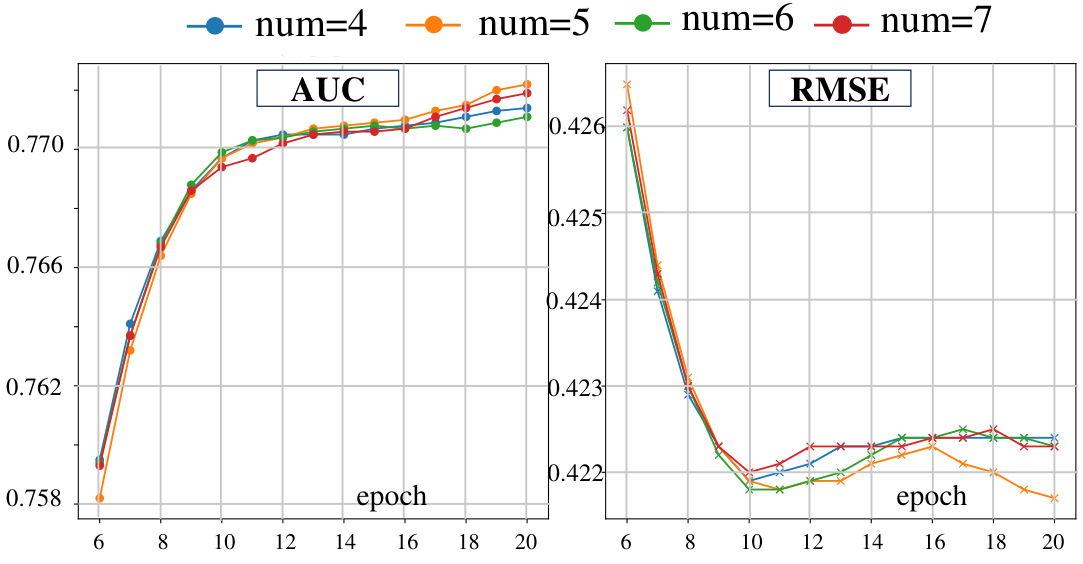
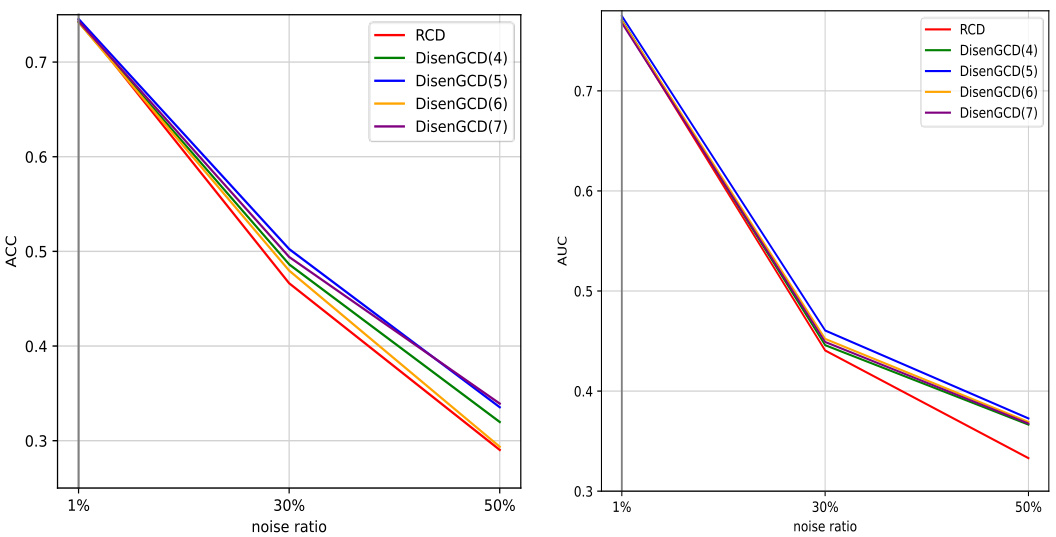
A robust model should maintain performance under various conditions. The paper’s robustness analysis is crucial, investigating the model’s resilience to noise in student interactions. DisenGCD, the proposed model, is shown to be more robust than existing models, particularly in noisy datasets. The analysis likely examines the impact of different noise levels, possibly adding random errors to student responses to simulate real-world imperfections. Key metrics, such as accuracy and AUC, are tracked to quantify the performance degradation under various noise intensities. The use of disentangled graphs in DisenGCD might be highlighted as a key factor in improving robustness. The authors likely compare their approach’s robustness to several baseline methods. The results section should numerically demonstrate how DisenGCD outperforms these baselines, solidifying its claim of superior robustness.
Diagnostic Function#
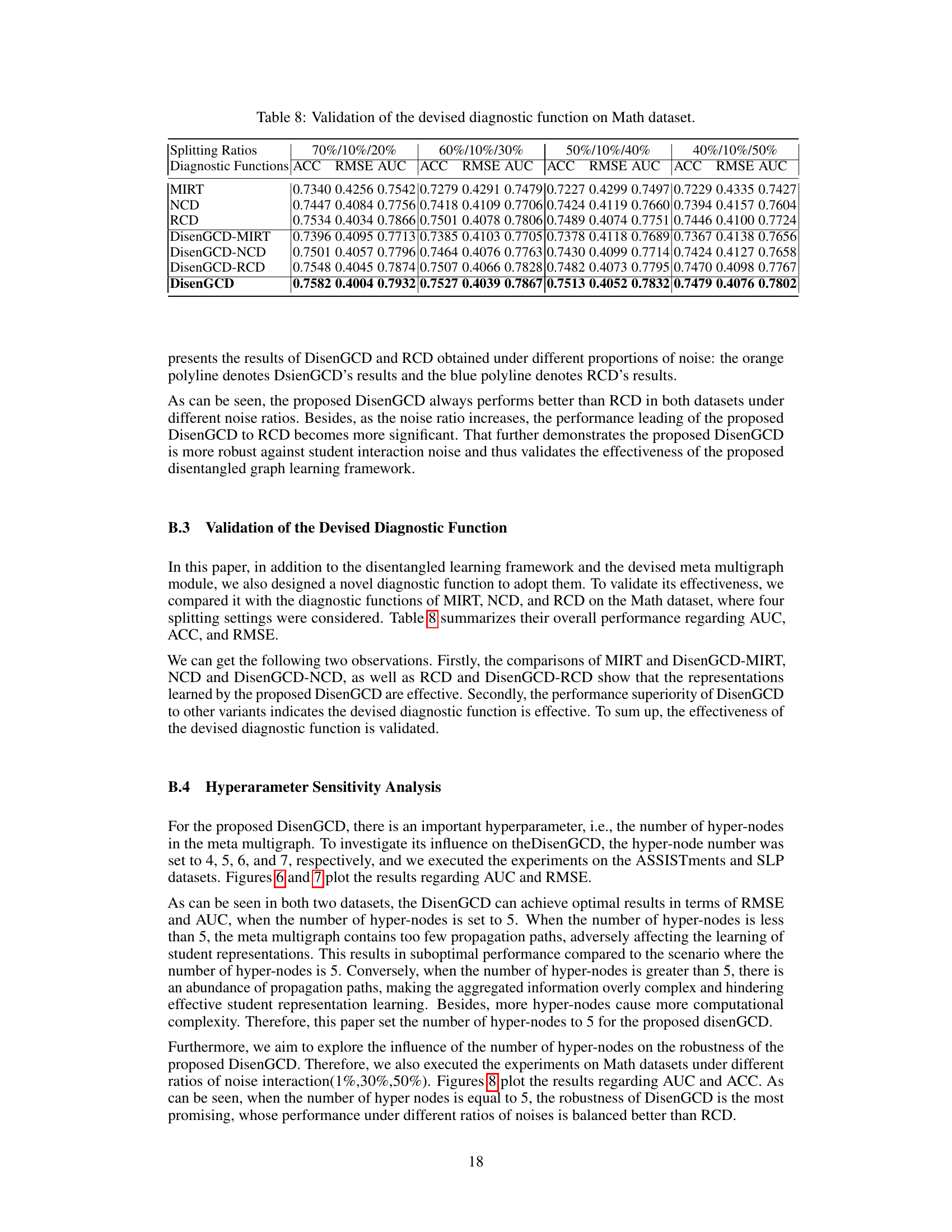
The diagnostic function in cognitive diagnosis (CD) models is crucial for translating learned representations into accurate student proficiency estimations. DisenGCD’s novel diagnostic function is particularly noteworthy because it directly handles three disentangled representations (student, exercise, and concept) simultaneously. This contrasts sharply with traditional CD models that implicitly intertwine these representations, potentially leading to inaccuracies when dealing with noisy or incomplete interaction data. By processing these representations separately and then combining them, DisenGCD’s diagnostic function can improve robustness and predictive accuracy. It leverages a multi-layer perceptron architecture to effectively combine the information, producing a final prediction of student mastery of the concepts. The function’s design incorporates a sigmoid function to produce probability scores, improving interpretability and facilitating the assessment of diagnostic accuracy. Furthermore, its integration with the disentangled meta-multigraph learning module allows lower-order exercise representations to enrich the student representation, making the overall diagnostic process more effective. The effectiveness of this approach is supported by experimental results demonstrating superior performance compared to state-of-the-art methods.
Future Directions#
Future research could explore enhancing DisenGCD’s scalability by investigating more efficient graph representation learning methods and developing approximation techniques for large-scale datasets. Addressing the limitations of relying on a single diagnostic function is another key area. Developing more sophisticated diagnostic functions that can better handle noise and uncertainty in student responses, perhaps incorporating techniques from probabilistic modeling, would improve robustness and accuracy. Investigating the impact of different graph structures and meta-graph designs on model performance is also crucial. Further experimentation with various types of GNNs and meta-graph learning strategies is needed. Finally, expanding the scope of DisenGCD to incorporate more diverse data sources, like contextual information, or applying it to other educational tasks beyond cognitive diagnosis, such as personalized learning recommendation systems, presents exciting opportunities. A comprehensive evaluation of DisenGCD’s fairness and robustness against various biases inherent in educational data is also important for wider adoption.
More visual insights#
More on figures
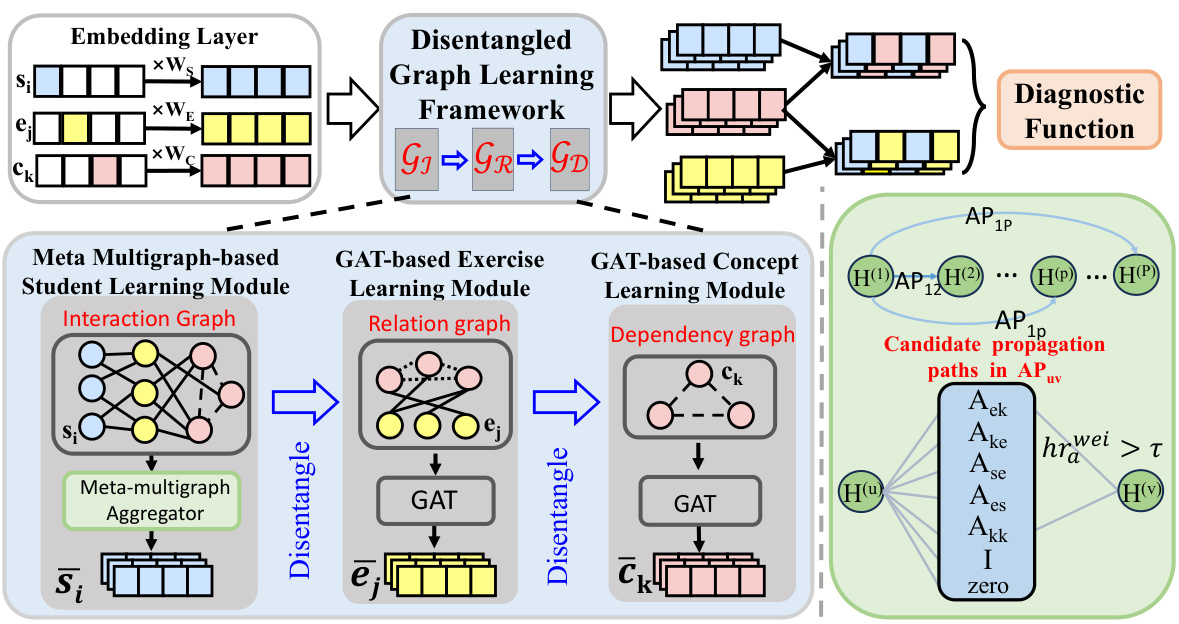
This figure presents the overall architecture of the DisenGCD model. It shows three learning modules working together: a meta multigraph-based student learning module (using interaction graph G1), a GAT-based exercise learning module (using relation graph GR), and a GAT-based concept learning module (using dependency graph GD). The meta-multigraph module is highlighted in green, showing its key role in learning student representation by enabling access to lower-order exercise latent representations via learnable propagation paths. Finally, a diagnostic function combines the three representations to make predictions.

This figure shows the architecture of the DisenGCD model. It consists of three main modules: a meta multigraph-based student learning module, a GAT-based exercise learning module, and a GAT-based concept learning module. The student module uses a meta-multigraph to learn student representations, while the exercise and concept modules use Graph Attention Networks (GATs) on disentangled graphs. These three modules’ outputs are then combined in a diagnostic function to make predictions.
This figure illustrates the architecture of the DisenGCD model. It consists of three main modules: a meta multigraph-based student learning module, a GAT-based exercise learning module, and a GAT-based concept learning module. Each module operates on a different disentangled graph (interaction graph, relation graph, and dependency graph) to learn respective representations for students, exercises, and concepts. The three representations are finally combined by a diagnostic function for prediction.
This figure shows the overall architecture of the DisenGCD framework. It’s composed of three main modules: a meta multigraph-based student learning module (using the interaction graph), a GAT-based exercise learning module (using the relation graph), and a GAT-based concept learning module (using the dependency graph). These modules learn representations for students, exercises, and concepts, respectively. The diagnostic function combines these representations to make a final prediction. The green part highlights the details of the meta multigraph module.
This figure provides a high-level overview of the DisenGCD framework. It shows three main modules: a meta multigraph-based module for student representation learning, and two GAT-based modules for exercise and concept representation learning. The three modules operate on three disentangled graphs derived from the student-exercise-concept interaction data. The meta-multigraph module is highlighted in green, indicating its key role in the framework.

This figure shows the architecture of the DisenGCD model. It is composed of three main modules: a meta multigraph-based student learning module, a GAT-based exercise learning module, and a GAT-based concept learning module. These modules learn representations from three disentangled graphs: student-exercise-concept interaction, exercise-concept relation, and concept dependency. The meta multigraph module is highlighted in green and details its internal workings. The three modules’ outputs are combined in a diagnostic function to make the final prediction.
This figure shows the architecture of the DisenGCD model. It consists of three main modules: a meta multigraph-based student learning module, a GAT-based exercise learning module, and a GAT-based concept learning module. These modules operate on three disentangled graphs: the student-exercise-concept interaction graph, the exercise-concept relation graph, and the concept dependency graph. The meta multigraph module uses multiple learnable propagation paths to enable the student representation to access lower-order exercise latent representations, leading to more effective and robust student representations. The GAT modules learn exercise and concept representations on their respective graphs, which are disentangled to increase robustness against interaction noise. Finally, a diagnostic function combines these representations to predict student performance.
More on tables
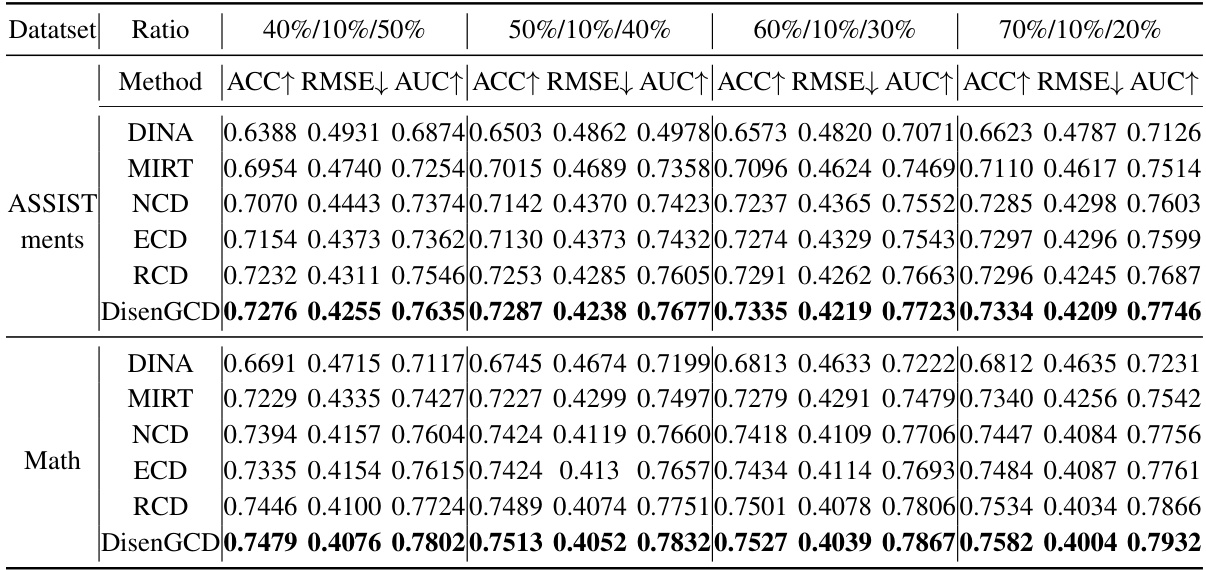
This table presents a performance comparison of DisenGCD against five other Cognitive Diagnosis Models (CDMs) using three metrics: Area Under the Curve (AUC), Accuracy (ACC), and Root Mean Squared Error (RMSE). The comparison is done on two datasets, ASSISTments and Math, using four different data splits. The best result for each metric and dataset is highlighted.

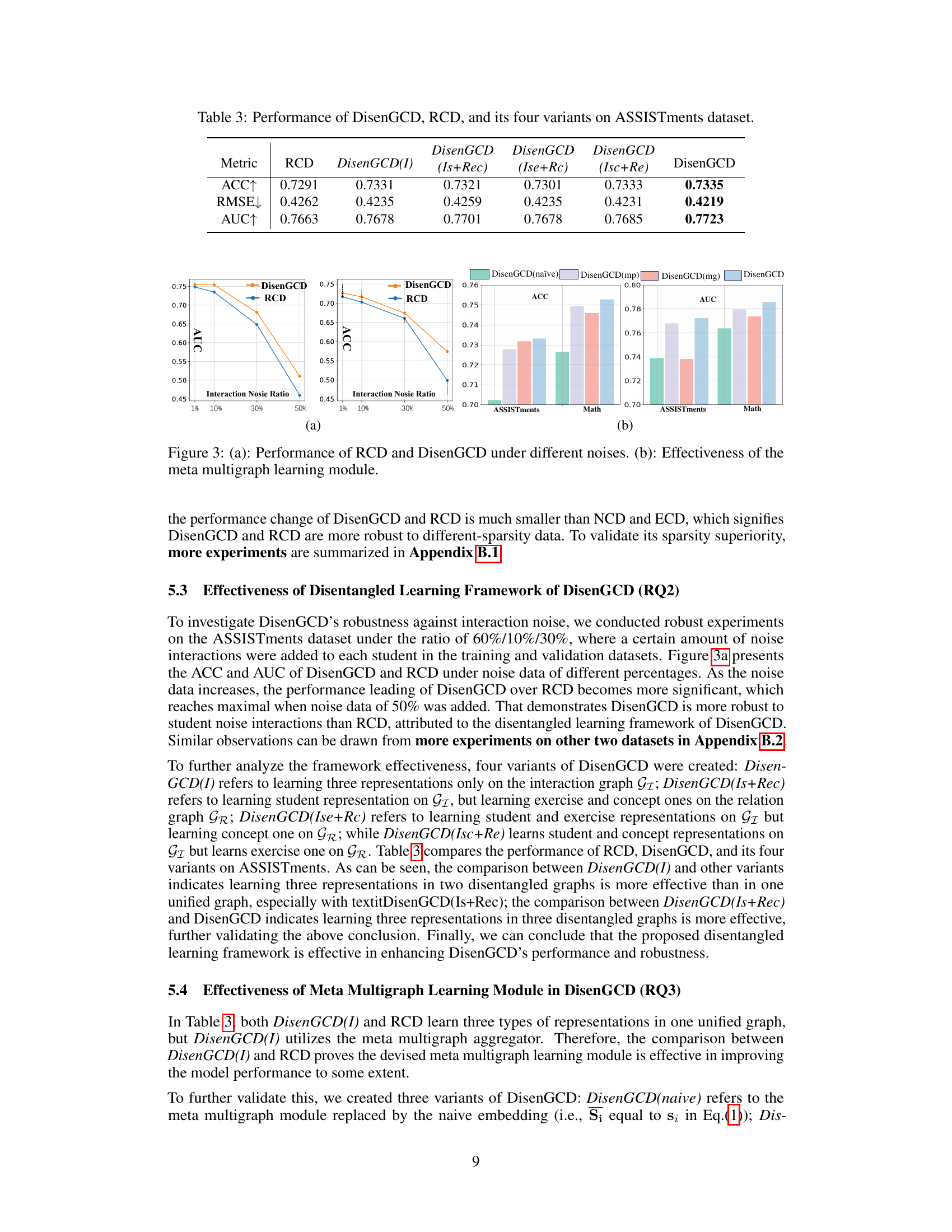
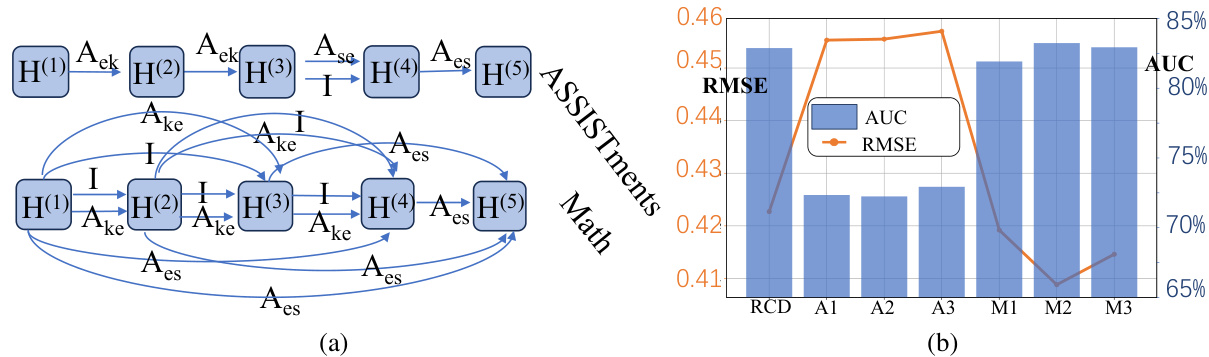
This table presents a comparison of the performance of DisenGCD and four of its variants against the baseline RCD model. The variants of DisenGCD explore different combinations of graph usage for learning the three representation types (student, exercise, concept) across the three disentangled graphs. DisenGCD(I) uses only the interaction graph, while the other variants combine the interaction graph with either the relation or dependency graph, or both, for learning the different representations. The metrics used for comparison are Accuracy (ACC), Root Mean Squared Error (RMSE), and Area Under the Curve (AUC). Higher ACC and AUC values and lower RMSE values indicate better performance.

This table presents a comparison of the performance of DisenGCD against five other Cognitive Diagnosis Models (CDMs) on two datasets: ASSISTments and Math. The performance metrics used are Area Under the Curve (AUC), Accuracy (ACC), and Root Mean Squared Error (RMSE). Four different data splits were used to evaluate the models’ robustness across different data configurations. The best result for each metric and dataset split is highlighted.
This table presents a comparison of the performance of DisenGCD against five other Cognitive Diagnosis Models (CDMs) on two datasets, namely ASSISTments and Math. The performance is measured using three metrics: Area Under the Curve (AUC), Accuracy (ACC), and Root Mean Squared Error (RMSE). Four different data splitting ratios (40%/10%/50%, 50%/10%/40%, 60%/10%/30%, and 70%/10%/20%) were used for training and testing. The best result for each metric in each dataset is highlighted.
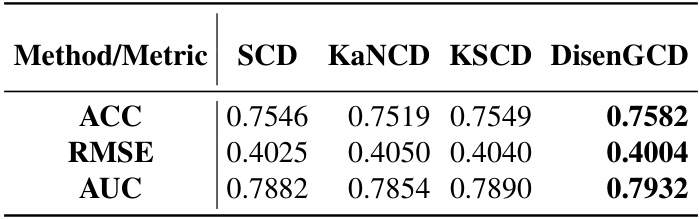
This table presents a comparison of the performance of four different cognitive diagnosis models (CDMs) on the Math dataset. The CDMs compared are SCD, KaNCD, KSCD, and the proposed DisenGCD model. The performance is evaluated using three metrics: Accuracy (ACC), Root Mean Squared Error (RMSE), and Area Under the Curve (AUC). Higher ACC and AUC values, and lower RMSE values indicate better performance.
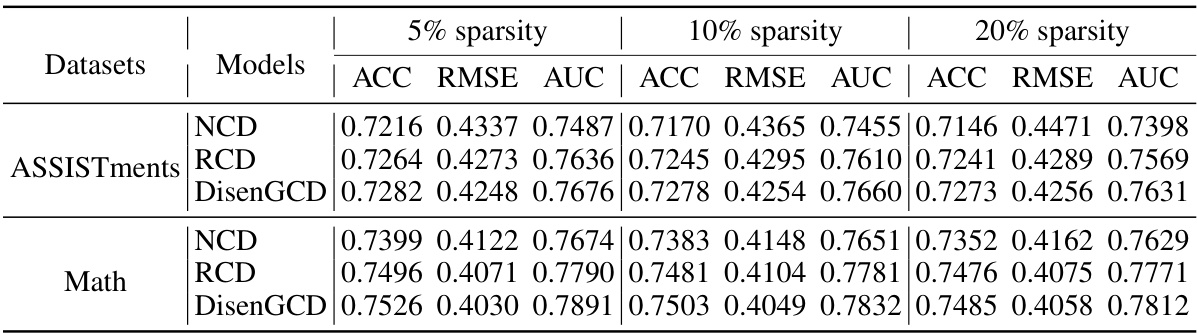
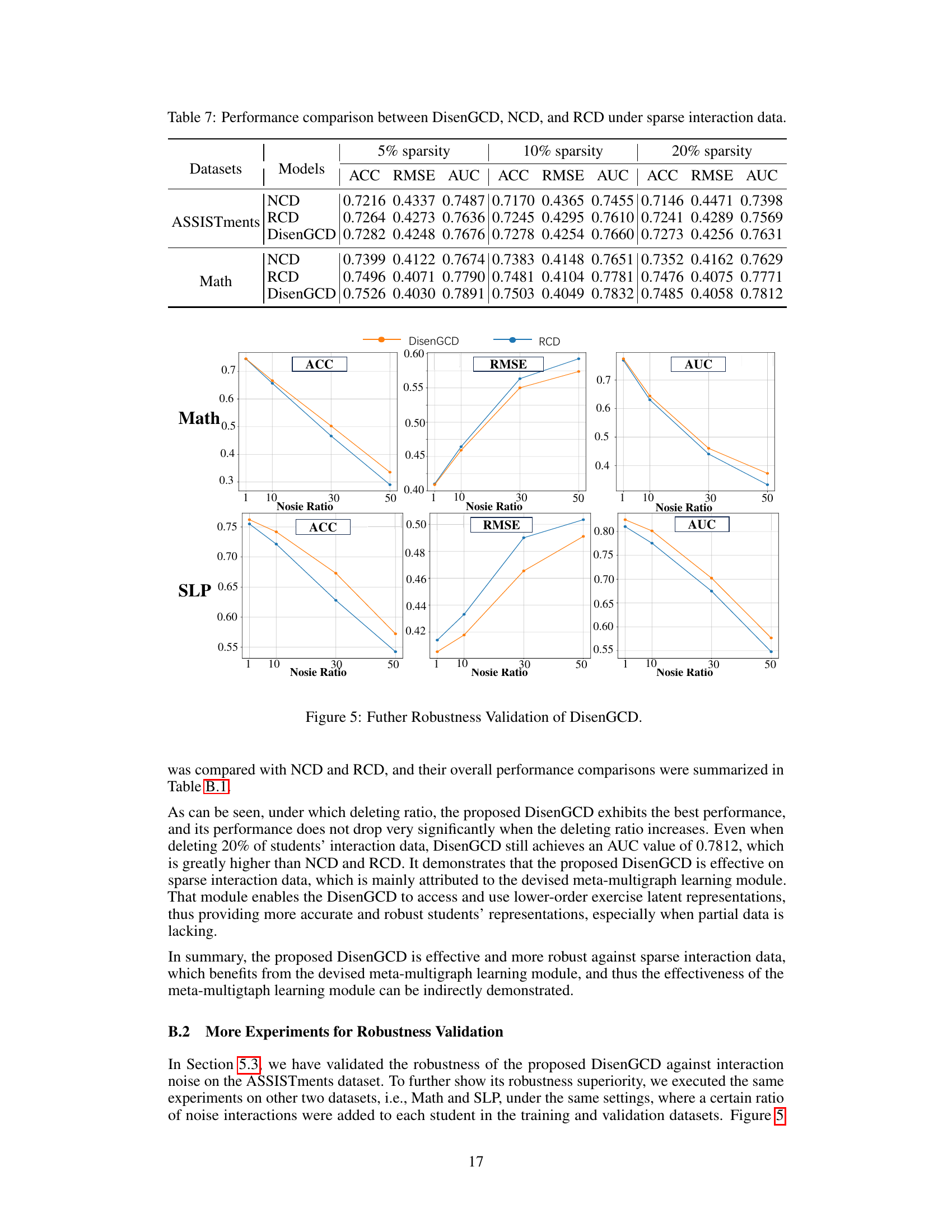
This table compares the performance of DisenGCD, NCD, and RCD models on two datasets (ASSISTments and Math) under different levels of data sparsity (5%, 10%, and 20%). The performance is evaluated using three metrics: Accuracy (ACC), Root Mean Squared Error (RMSE), and Area Under the Curve (AUC). The results show how well each model handles missing data in the student-exercise interactions.
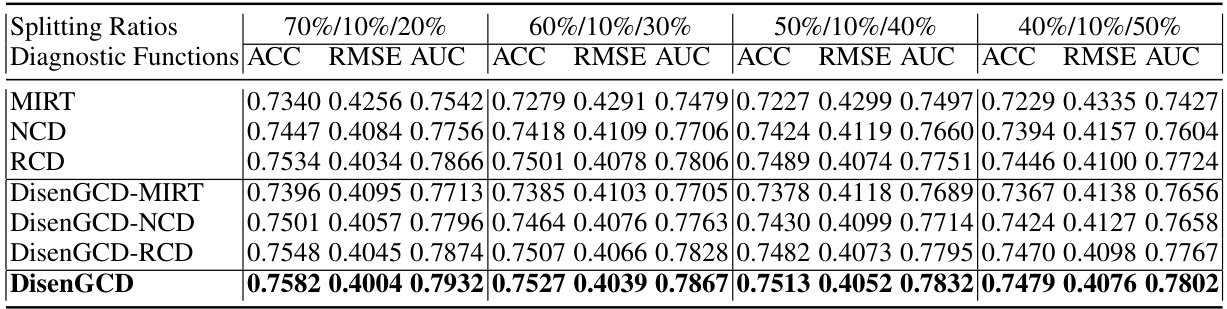
This table presents a comparison of the performance of DisenGCD against five other Cognitive Diagnosis Models (CDMs) on two datasets: ASSISTments and Math. The performance is measured using three metrics: Area Under the Curve (AUC), Accuracy (ACC), and Root Mean Squared Error (RMSE). Four different dataset splitting ratios were used to ensure robustness of the results. The best result for each metric on each dataset is highlighted in bold.
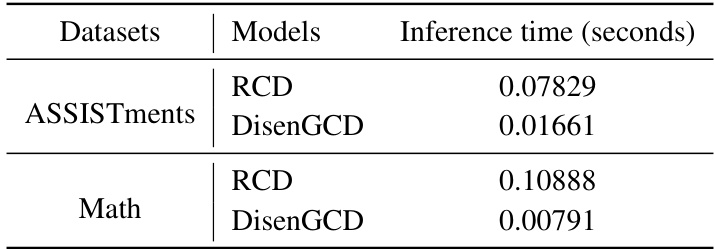
This table presents the performance comparison of DisenGCD against five other Cognitive Diagnosis Models (CDMs) across four different dataset splitting ratios. The metrics used for comparison are Area Under the Curve (AUC), Accuracy (ACC), and Root Mean Squared Error (RMSE). The best performance for each metric on each dataset is highlighted.

This table presents a comparison of the performance of DisenGCD against five other cognitive diagnosis models (CDMs) across four different data splits. The performance metrics used are AUC (Area Under the Curve), ACC (Accuracy), and RMSE (Root Mean Squared Error). The best performance for each metric and dataset is highlighted.

This table presents a comparison of the performance of DisenGCD against three other state-of-the-art Cognitive Diagnosis Models (CDMs): SCD, KaNCD, and KSCD. The comparison is done using the Math dataset and considers three evaluation metrics: Accuracy (ACC), Root Mean Squared Error (RMSE), and Area Under the Curve (AUC). Higher ACC and AUC values, and lower RMSE values indicate better performance.
Full paper#