↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Point cloud interpolation (PCI) is essential for creating smooth and continuous point cloud sequences from sparse temporal information. However, current methods struggle with complex spatiotemporal dynamics and point sparsity, often failing to accurately reconstruct intermediate frames. This is especially true when dealing with non-rigid deformations and unordered point cloud data, prevalent in applications such as autonomous driving and virtual reality.
NeuroGauss4D-PCI addresses these challenges by employing a multi-stage method involving iterative Gaussian soft clustering to achieve structured point cloud representations, temporal radial basis function Gaussian residuals to capture temporal dynamics, and a 4D Gaussian deformation field to model continuous spatiotemporal deformations. The method fuses geometric features from the Gaussian deformation fields and latent features from a 4D neural field, achieving significantly improved interpolation accuracy and efficiency compared to existing approaches. The algorithm’s effectiveness is demonstrated across different datasets, including both object-level and large-scale autonomous driving scenarios, showcasing its robustness and generalizability.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel and effective method for point cloud interpolation, a crucial task in various applications like autonomous driving and virtual reality. The method’s superior performance and efficiency, especially when dealing with complex non-rigid deformations and large-scale scenes, make it highly relevant to current research trends and opens new avenues for future research in temporal point cloud processing.
Visual Insights#

This figure compares the performance of NeuroGauss4D-PCI against other state-of-the-art methods for point cloud interpolation. The left panel shows interpolation error on the DHB dataset for different numbers of interval frames. The right panel displays interpolation error on the NL-Drive dataset for different point cloud densities. In both cases, NeuroGauss4D-PCI significantly outperforms other methods, demonstrating its robustness to various challenges like non-rigid deformations, large-scale scenes and data sparsity.

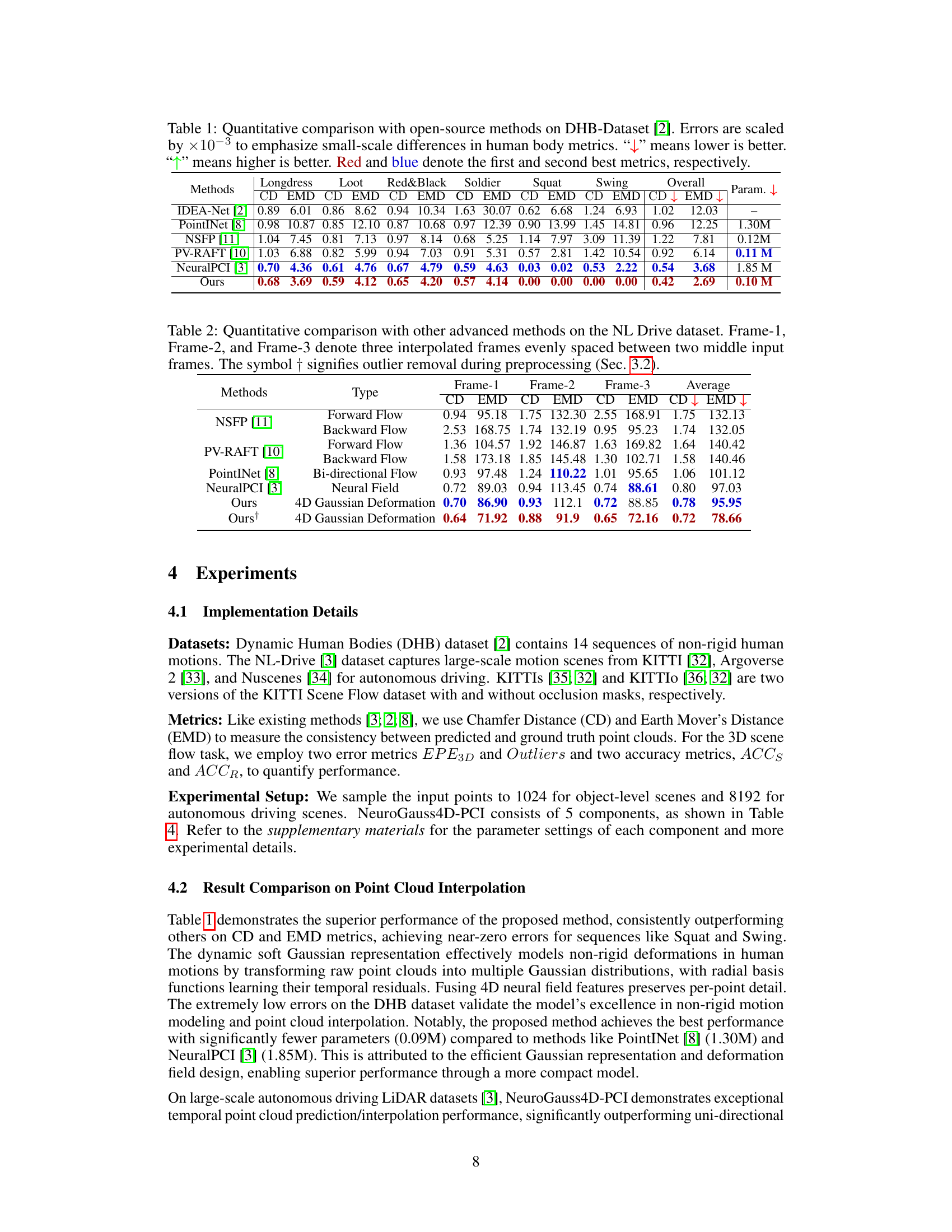
This table presents a quantitative comparison of the proposed NeuroGauss4D-PCI method against several existing open-source methods for point cloud interpolation. The comparison is performed on the Dynamic Human Bodies (DHB) dataset [2], focusing on the metrics of Chamfer Distance (CD) and Earth Mover’s Distance (EMD). The table details the performance of each method across different categories of human poses (Longdress, Loot, Red & Black, Soldier, Squat, Swing) and provides the overall average performance. Lower values are better for both CD and EMD. The table also indicates the number of parameters used by each method.
In-depth insights#
4D Gaussian Fields#
The concept of “4D Gaussian Fields” in the context of point cloud interpolation suggests a powerful approach to modeling spatiotemporal data. A standard Gaussian distribution is defined by its mean and covariance matrix, representing the location and spread of a probability distribution in 3D space. Extending this to 4D incorporates time as an additional dimension, allowing us to capture the dynamics of a point cloud over time. This approach offers several advantages. It provides a smooth and continuous representation of the evolution of a point cloud, naturally handling non-rigid deformations and complex motions. The Gaussian framework offers an elegant way to model uncertainty, allowing for more robust interpolation in sparse or noisy data. By parameterizing the Gaussian fields with neural networks, we gain flexibility, potentially learning complex spatiotemporal dependencies and effectively capturing residual motions. The success of this method hinges on the efficient design of the neural network architecture and how well it integrates with the Gaussian framework. Furthermore, a 4D representation is crucial for efficient interpolation, avoiding the need for pairwise comparisons between frames common in other methods.
Temporal RBF-GR#
The Temporal Radial Basis Function Gaussian Residual (RBF-GR) module is a crucial component, bridging the gap between discrete time steps and continuous spatiotemporal modeling. It leverages radial basis functions (RBFs) to smoothly interpolate Gaussian parameters (means, covariance matrices, and features) across time. The RBFs’ adaptability enables the module to capture complex temporal dynamics, and this interpolation ensures smooth transitions in the Gaussian distributions. The learnable parameters of the RBFs (centers and scales) allow the model to adapt to varying temporal patterns and characteristics of the data, enhancing the model’s expressiveness and accuracy. The RBF-GR module’s output serves as the input for subsequent processing steps, such as the 4D Gaussian Deformation Field, which further refines the spatiotemporal representation. In essence, the RBF-GR module’s role is to make the continuous dynamics of Gaussian parameters explicit, thereby greatly improving the interpolation quality and the model’s overall performance.
PCI Challenges#
Point cloud interpolation (PCI) faces significant challenges due to the inherent nature of point cloud data and the complexity of real-world dynamic scenes. Sparsity is a major hurdle, as point clouds often lack the density of images, making it difficult to accurately reconstruct intermediate frames. The unordered nature of point clouds further complicates the task, requiring sophisticated algorithms to manage the lack of inherent structure. Complex spatiotemporal dynamics present a substantial challenge. Non-rigid motions, occlusions, and nonlinear trajectories make it difficult for models to accurately predict intermediate frames. The spatiotemporal correlation of points across multiple frames also needs to be accurately captured, posing a significant modeling challenge. Finally, the success of PCI hinges on effectively handling sparse temporal samples, meaning reliable interpolation from limited data. Models must generalize well and avoid making assumptions which may not hold true for real-world scenarios.
Ablation Study#
The ablation study systematically evaluates the contribution of each component in the proposed NeuroGauss4D-PCI model. By progressively removing components—the neural field, Gaussian point cloud representation, temporal RBF-Gaussian residual module, and the 4D deformation field—the authors quantify the impact on performance metrics (CD and EMD) on both DHB and NL-Drive datasets. The results clearly demonstrate the critical role of the neural field in capturing spatio-temporal features, showing a significant performance drop when removed. The 4D deformation field is also crucial, substantially improving performance when included. The study’s findings highlight the complementary strengths of each module, underscoring the synergistic effect of combining neural fields and geometric representations for point cloud interpolation. Further, the ablation study’s methodical approach provides strong evidence for the design choices made and strengthens the overall claims of the paper.
Future of PCI#
The future of Point Cloud Interpolation (PCI) lies in addressing its current limitations and leveraging emerging technologies. Improving robustness to noise and outliers is crucial, especially in real-world scenarios with sensor limitations. Developing methods capable of handling dynamic, non-rigid deformations more accurately is essential for applications such as autonomous driving and human motion capture. This requires moving beyond linear interpolation techniques and embracing more sophisticated models of temporal dynamics. Furthermore, efficient handling of large-scale point clouds is vital for scalability. This might involve novel data structures or compression algorithms, and perhaps leveraging parallel computing techniques more effectively. Finally, integrating PCI with other modalities, such as images or inertial measurements, could significantly improve the accuracy and robustness of the final interpolated results, thus enabling a greater understanding of 4D scenes.
More visual insights#
More on figures

This figure illustrates the Temporal Radial Basis Function Gaussian Residual (RBF-GR) module and the 4D Gaussian Deformation Field. The RBF-GR module uses radial basis functions to interpolate Gaussian parameters over time, capturing temporal dynamics. The 4D Gaussian Deformation Field uses Gaussian means, covariances, and features to model spatiotemporal changes in the Gaussian distributions, which are then used to update Gaussian ellipsoid information. The figure shows the different components of the module and how they interact to generate updated ellipsoid information.

This figure compares the performance of the proposed NeuroGauss4D-PCI method against other state-of-the-art point cloud interpolation algorithms (NeuralPCI [3] and 3DSFLabelling [9]) on the NL Drive autonomous driving dataset. It visually demonstrates that NeuroGauss4D-PCI achieves better alignment with the ground truth point cloud positions and geometry when interpolating between frames. The better alignment between the predicted points (orange) and the ground truth points (green) highlights the improved accuracy of NeuroGauss4D-PCI in handling the complexities of large-scale LiDAR scenes.
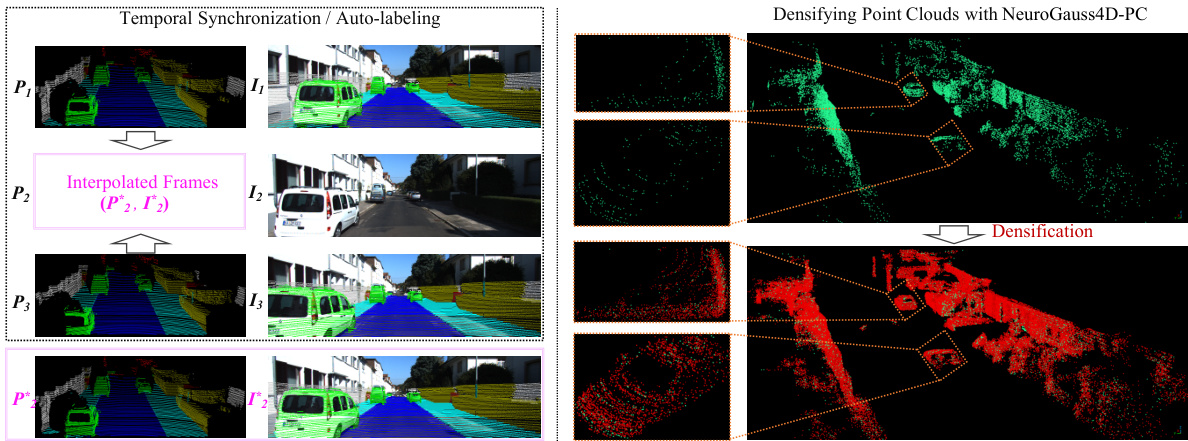
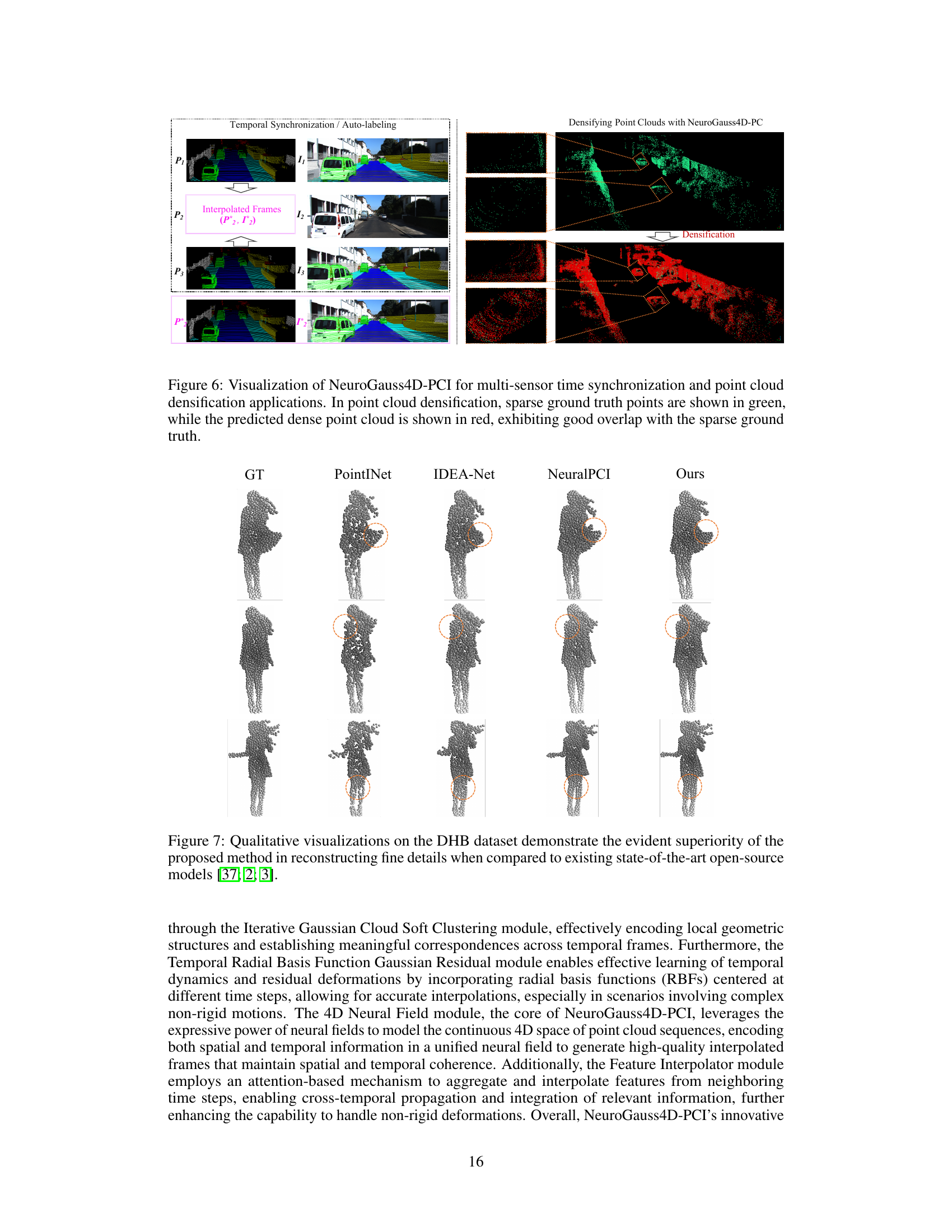
This figure demonstrates two applications of the NeuroGauss4D-PCI model: temporal synchronization and point cloud densification. The left side shows how the model can interpolate intermediate frames between sparse LiDAR point clouds (P1, P3) and image frames (I1, I3) to produce temporally consistent sequences (P2, I2). The right side illustrates how the model can densify sparse point clouds (green) by predicting additional points (red), increasing the point density while maintaining spatial accuracy. The close overlap between green and red points indicates accurate predictions.

This figure shows a qualitative comparison of point cloud interpolation results on the DHB dataset. It compares the ground truth (GT) with results from PointINet, IDEA-Net, NeuralPCI, and the proposed NeuroGauss4D-PCI method. The focus is on highlighting the superior ability of NeuroGauss4D-PCI to accurately reconstruct fine details and handle complex non-rigid deformations, particularly in areas indicated by the orange dashed circles.

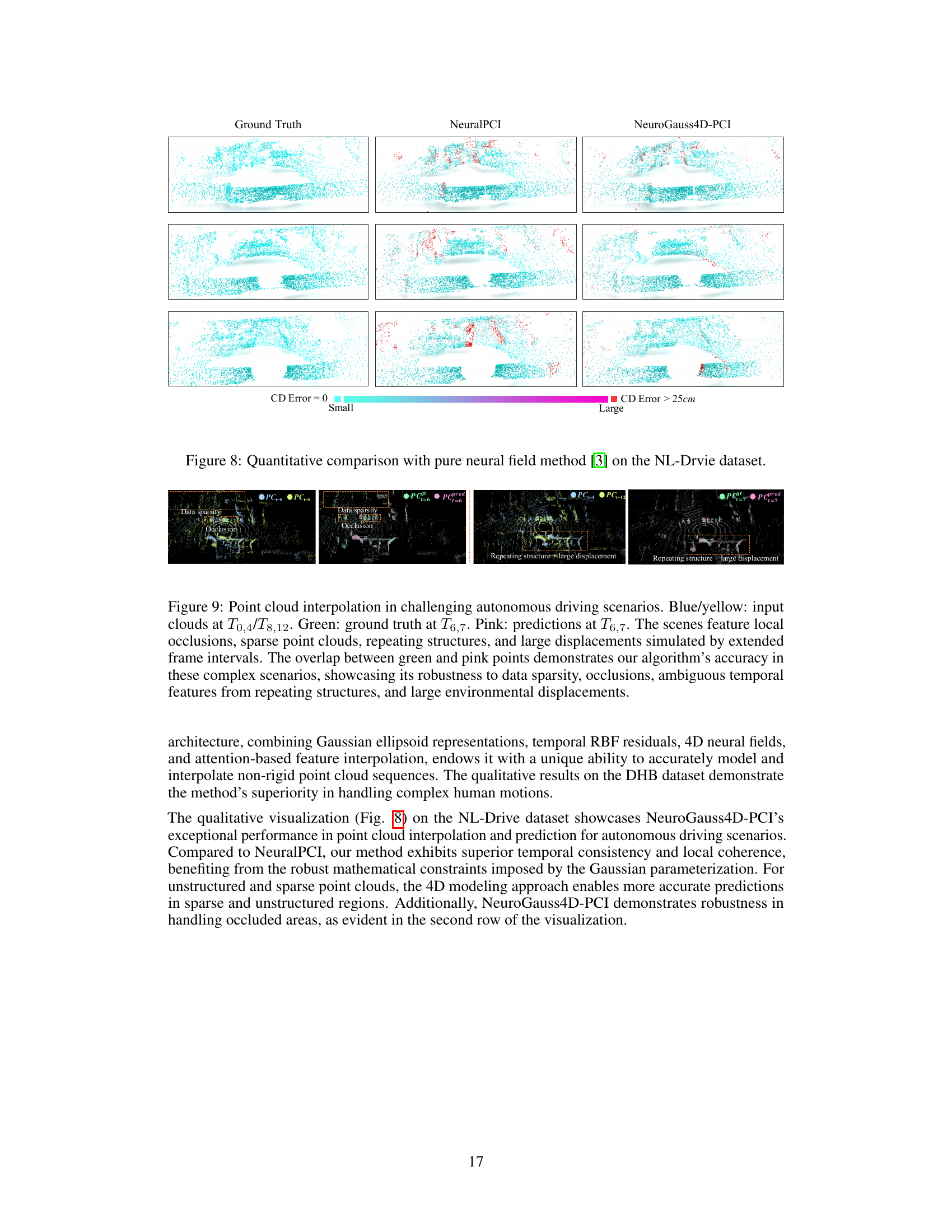
This figure shows a quantitative comparison of the proposed NeuroGauss4D-PCI method against a pure neural field method [3] on the NL-Drive dataset. It visually compares the ground truth point clouds to the results from both methods. The color-coding represents the Chamfer distance (CD) error, with blue indicating perfect matches (CD Error = 0) and progressively warmer colors representing increasing error, culminating in red (CD Error > 25cm). The figure likely demonstrates NeuroGauss4D-PCI’s improved accuracy in point cloud interpolation, particularly for larger-scale scenes.

This figure shows the results of point cloud interpolation in challenging autonomous driving scenarios. The input point clouds are shown in blue and yellow, the ground truth in green, and the model’s predictions in pink. The scenarios include local occlusions, sparse data, repeating structures, and large displacements. The overlap between the ground truth and predictions demonstrates the robustness of the algorithm to these challenges.
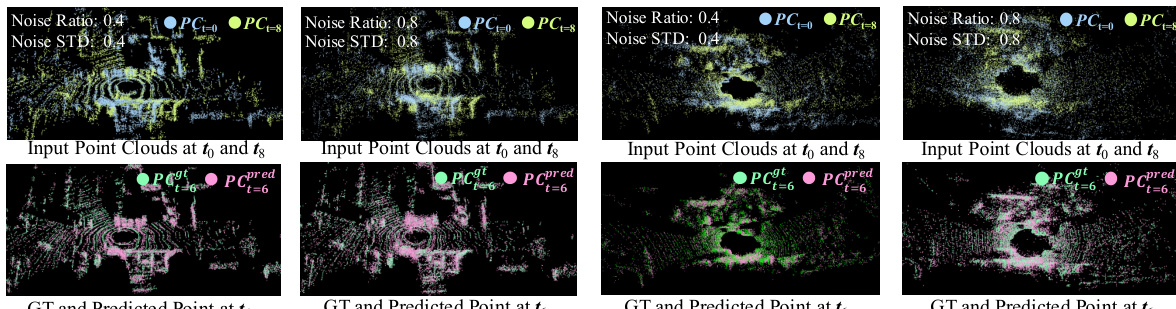
This figure shows the robustness test of the proposed method under different noise levels. The top row displays the input point clouds with varying levels of added Gaussian noise (different noise ratios and standard deviations). The bottom row compares the ground truth point cloud at a specific time point (t=6) with the point cloud predicted by the model under each noise condition. The alignment between the ground truth (green) and predicted (pink) points illustrates the accuracy of the method under different noise levels, highlighting its resilience to noise.
More on tables

This table presents a quantitative comparison of the proposed NeuroGauss4D-PCI method with several existing open-source point cloud interpolation methods on the Dynamic Human Body (DHB) dataset. The comparison uses two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). Results are presented for multiple body poses (Longdress, Loot, Red&Black, Soldier, Squat, Swing) and an overall average, showing the performance of each method in terms of interpolation accuracy. Lower values are better for both CD and EMD, indicating higher accuracy.

This table presents a quantitative comparison of the proposed NeuroGauss4D-PCI method with several other open-source methods for point cloud interpolation on the Dynamic Human Bodies (DHB) dataset. The comparison is based on two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). The table shows the performance of each method across various categories of human body poses, with lower scores indicating better performance. Error values are scaled down by a factor of 1000 to highlight the subtle differences in performance between the methods.

This table presents a quantitative comparison of the proposed NeuroGauss4D-PCI method with several other open-source point cloud interpolation methods on the Dynamic Human Body (DHB) dataset. The comparison uses two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). The table is broken down by different motion categories within the DHB dataset (Longdress, Loot, Red&Black, Soldier, Squat, Swing), showing the performance of each method on each category and providing an overall average performance. The table also shows the number of parameters for each model, indicating model complexity.
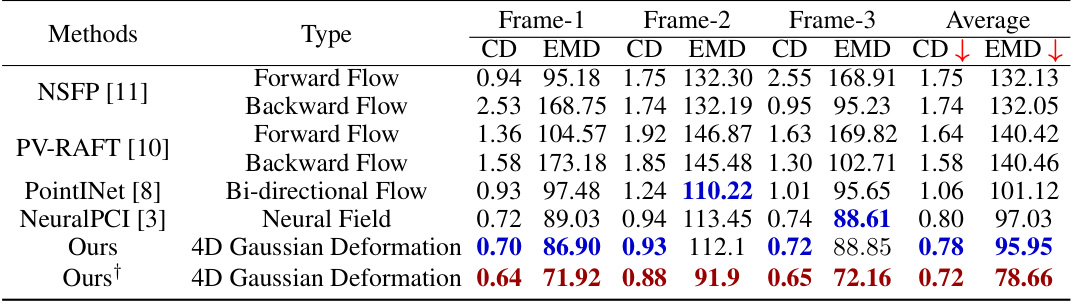
This table compares the performance of the proposed NeuroGauss4D-PCI method against other state-of-the-art methods for point cloud interpolation on the NL-Drive dataset. The NL-Drive dataset is challenging due to its large scale and inclusion of autonomous driving scenarios. The table shows the Chamfer Distance (CD) and Earth Mover’s Distance (EMD) errors for three interpolated frames (Frame-1, Frame-2, Frame-3) between two input frames. Lower CD and EMD values indicate better performance. The symbol † indicates that outlier removal preprocessing was used.
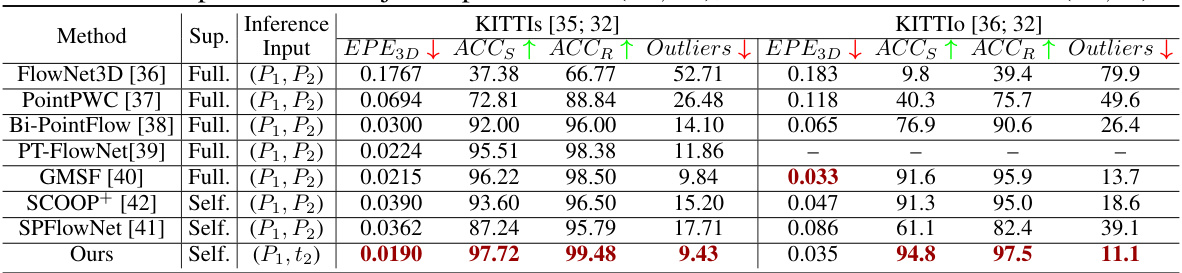
This table compares the proposed NeuroGauss4D-PCI method against state-of-the-art techniques for point cloud scene flow estimation using the KITTI and KITTIo datasets. It contrasts self-supervised (‘Self’) and fully-supervised (‘Full’) approaches and highlights the input type used. The key metrics compared are EPE3D (Endpoint Error in 3D), ACCS (Accuracy of Scene Flow), ACCR (Accuracy of Correspondence), and Outliers. Lower EPE3D and Outliers values are preferred, while higher ACCS and ACCR values are better.

This ablation study analyzes the impact of each component (Neural Field, Gaussian Point Cloud, Temporal RBF Gaussian Residual, 4D Deformation Field, LG-Cat, and Fast-LG-Fusion) on the overall performance of the NeuroGauss4D-PCI model, evaluating Chamfer Distance (CD) and Earth Mover’s Distance (EMD) on the DHB and NL-Drive datasets. The results show the contribution of each component towards achieving the best performance and highlight the effectiveness of the proposed approach in accurately capturing the spatio-temporal characteristics of point clouds.
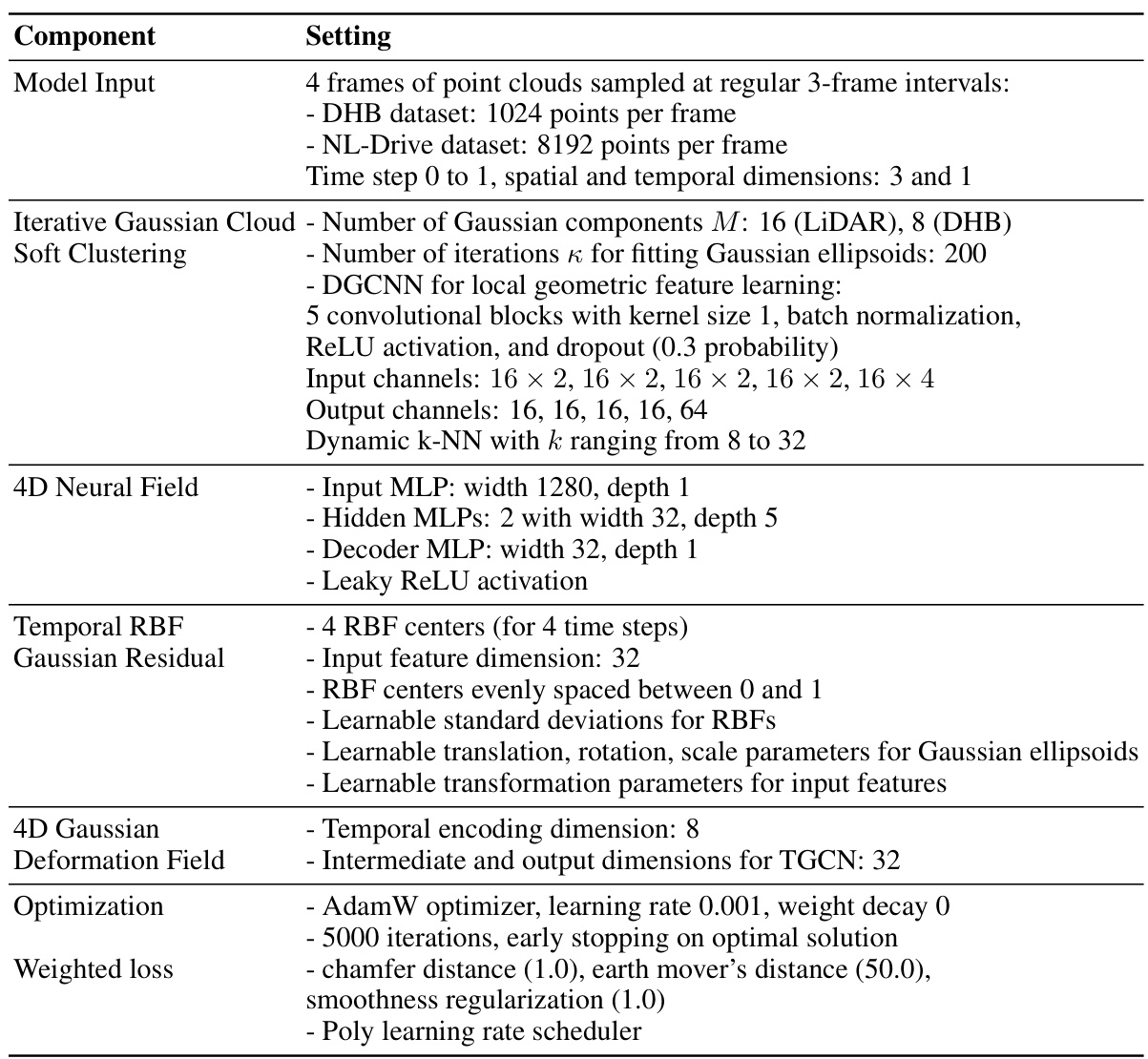
This ablation study analyzes the impact of each component of the NeuroGauss4D-PCI model on two datasets: DHB and NL-Drive. It shows the performance effects of removing or including the neural field, Gaussian point cloud representation, temporal radial basis function Gaussian residual module, 4D Gaussian deformation field, and different feature fusion methods. The results highlight the importance of each component for achieving optimal performance.
Full paper#