↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline policy evaluation (OPE) is crucial for deploying reinforcement learning (RL) in high-stakes scenarios where online experimentation is infeasible. However, OPE often struggles with non-stationarity issues like unobserved confounding or distributional shifts between historical and future data. Existing OPE methods often lack robustness and efficiency in addressing these problems, leading to unreliable policy evaluations.
This work presents a novel solution that tackles these limitations. The authors propose a perturbation model that allows for changes in transition kernel densities within a specified range, thus capturing various uncertainty sources. They develop a sharp and efficient estimator, which is also insensitive to errors in the estimation of nuisance functions, such as worst-case Q-functions. The method is validated numerically and shown to provide valid bounds even with inconsistent nuisance estimation. The work combines robustness, orthogonality, and finite-sample inference to enhance the credibility and reliability of offline policy evaluation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning and causal inference because it offers a novel, statistically efficient method for offline policy evaluation that is robust to real-world issues like unobserved confounding and environmental shifts. It provides new theoretical guarantees and practical tools for creating reliable policy evaluations, addressing a major challenge in deploying RL in high-stakes applications. The approach has implications beyond the specific methods, offering broader insights into developing robust and efficient estimators in related areas.
Visual Insights#

This figure illustrates the concept of Conditional Value at Risk (CVaR) for a given distribution. The x-axis represents the possible values of a random variable v(s’) conditioned on state s and action a. The y-axis represents the probability density of v(s’). The curve shows the probability density function of v(s’). The shaded regions represent the lower and upper tails of the distribution, which correspond to CVaR⁻(s, a) and CVaR⁺(s, a), respectively. The values β⁻(s, a) and β⁺(s, a) are the quantiles that define the boundaries of these tail regions. E[v(s’)|s,a] shows the expectation of v(s’)|s,a.
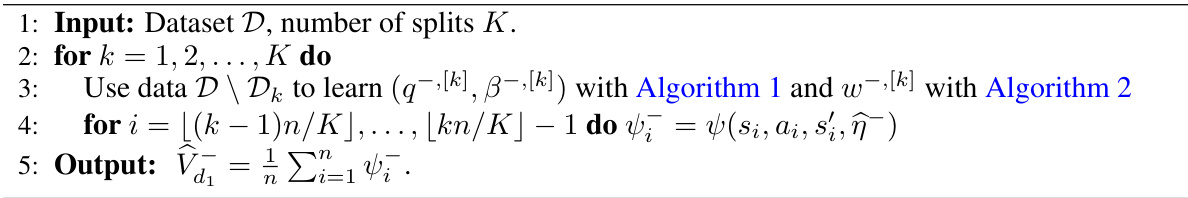
This table presents the results of synthetic data experiments evaluating three different estimators (Q, W, and Orth) for estimating the worst-case policy value (Vd1) under four different values of the sensitivity parameter A. The above section shows box plots visualizing the range of policy value estimates for each estimator and A value, with horizontal lines indicating the true worst-case values. The below section provides a numerical comparison, presenting the mean squared error (MSE) of each estimator relative to the true worst-case policy value, along with standard deviations.
In-depth insights#
Robust OPE#
Robust offline policy evaluation (OPE) tackles the challenge of evaluating a policy’s performance when the test environment might differ from the training environment. This is crucial because historical data used for training may not accurately reflect future conditions. Robust OPE methods aim to provide reliable policy value estimates even under environmental shifts, such as unmeasured confounding or distributional changes. This robustness is achieved by considering a range of possible test environments, often using techniques from robust optimization or sensitivity analysis. Key considerations in robust OPE include defining a suitable model for environmental uncertainty, which dictates how much the test environment can vary from the training environment, and developing efficient estimators that provide valid bounds on the policy value given data from the original MDP. The effectiveness of a robust OPE method is demonstrated by its ability to produce accurate and reliable results despite uncertainty about the test environment. Furthermore, statistical guarantees, such as asymptotic normality and semiparametric efficiency, are desirable properties in robust OPE estimators to facilitate reliable inference.
Sharp Bounds#
The concept of “sharp bounds” in the context of a research paper likely refers to the most precise or tightest possible limits that can be placed on a particular value or parameter, given the available data and assumptions. This implies a focus on minimizing the uncertainty associated with the estimation, preventing overly conservative or overly optimistic conclusions. The methods used to derive these sharp bounds are crucial; they may involve advanced statistical techniques, such as semiparametric efficiency, which aim to extract maximum information from limited data while minimizing bias. The study’s robustness is linked directly to how well these sharp bounds hold under various conditions or perturbations. Demonstrating that the estimated bounds are indeed sharp requires rigorous theoretical justification and careful consideration of potential confounding factors. Overall, the pursuit of sharp bounds highlights a commitment to precise and reliable inference, even within the challenges of real-world data limitations.
Orthogonal Estimator#
The concept of an orthogonal estimator is crucial in this research paper because it directly addresses the challenges of efficient and robust off-policy evaluation in the presence of uncertainty. Orthogonal estimators are designed to be insensitive to errors in the estimation of nuisance parameters, such as Q-functions or density ratios. This robustness is a critical advantage in the context of robust Markov Decision Processes (MDPs), where the true environment dynamics might deviate from those observed during training. By achieving orthogonality, the proposed estimator guarantees reliable policy value estimation even when nuisance functions are estimated at slower non-parametric rates. Furthermore, the estimator is shown to be semiparametrically efficient, implying it achieves the minimum asymptotic variance among all regular and asymptotically linear estimators. This combination of properties makes the orthogonal estimator a powerful tool for credible and reliable policy evaluation in complex and uncertain scenarios.
Minimax Learning#
Minimax learning tackles the challenge of training models that perform well even under worst-case scenarios, effectively addressing uncertainty and adversarial situations. It frames learning as a game between a model and an adversary, where the model aims to minimize its maximum loss across all possible adversarial strategies. This approach is particularly valuable when the environment or data distribution is uncertain or subject to manipulation. A key aspect is finding the optimal balance between model complexity and robustness, avoiding overfitting to specific adversarial examples while maintaining performance in a broad range of conditions. The minimax framework offers strong theoretical guarantees on model performance and is applicable to diverse machine learning tasks, making it a potent tool for building reliable and robust systems in uncertain environments. The practical application of minimax often involves computationally intensive methods for finding the minimax solution, which is a major consideration in algorithm design and implementation.
Future Work#
Future research directions stemming from this robust offline policy evaluation work could explore several promising avenues. Extending the current framework to handle more complex uncertainty models, beyond the multiplicative perturbation model considered here, is crucial for real-world applicability. This might involve incorporating additive noise or exploring different types of distributional shifts. Another key area is developing more efficient algorithms for estimating the necessary nuisance functions, particularly in high-dimensional settings. The current methods rely on function approximation techniques, and improvements in efficiency and accuracy could significantly enhance the practical utility of the approach. Investigating the impact of different logging policies on the robustness and accuracy of the evaluation could shed light on the optimal data collection strategies for different applications. This includes scenarios with unobserved confounding, where the logged data may not fully reflect the true environment dynamics. Finally, applying this methodology to larger-scale real-world problems is essential to assess the robustness and scalability of the approach in challenging settings. This should include detailed evaluations across various domains, with a rigorous assessment of the trade-offs between robustness, efficiency, and computational cost.
More visual insights#
More on tables

The table presents the results of synthetic data experiments comparing three different estimators for estimating the worst-case policy value in a robust Markov Decision Process (MDP). The estimators are Q (RobustFQE), W (RobustMIL), and Orth (orthogonal estimator). The results are shown for four different values of the sensitivity parameter A, representing the degree of uncertainty in the transition dynamics. The table includes box plots visualizing the range of policy value estimates and a table summarizing the mean squared error (MSE) for each estimator and the true worst-case policy value. The MSE values are reported along with standard deviation errors.

The table presents the median policy value estimates obtained using three different methods (Q, W, Orth) for estimating the worst-case policy value in a sepsis management application. The results are shown for different values of the sensitivity parameter (Λ), representing various levels of uncertainty in the transition dynamics. The ± values indicate the spread of estimates, calculated as half the difference between the 80th and 20th percentiles across multiple runs with different random seeds.
Full paper#



















