Efficient and Private Marginal Reconstruction with Local Non-Negativity

↗ arXiv ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces efficient post-processing methods for reconstructing answers to marginal queries in differentially private data release. This addresses a critical subproblem in achieving high-dimensional data privacy while minimizing error and computation time. The proposed methods, particularly GReM-LNN, improve upon existing techniques, making them more suitable for large datasets. Furthermore, the techniques can be applied to various private query answering mechanisms, expanding their potential impact.

Visual Insights

#

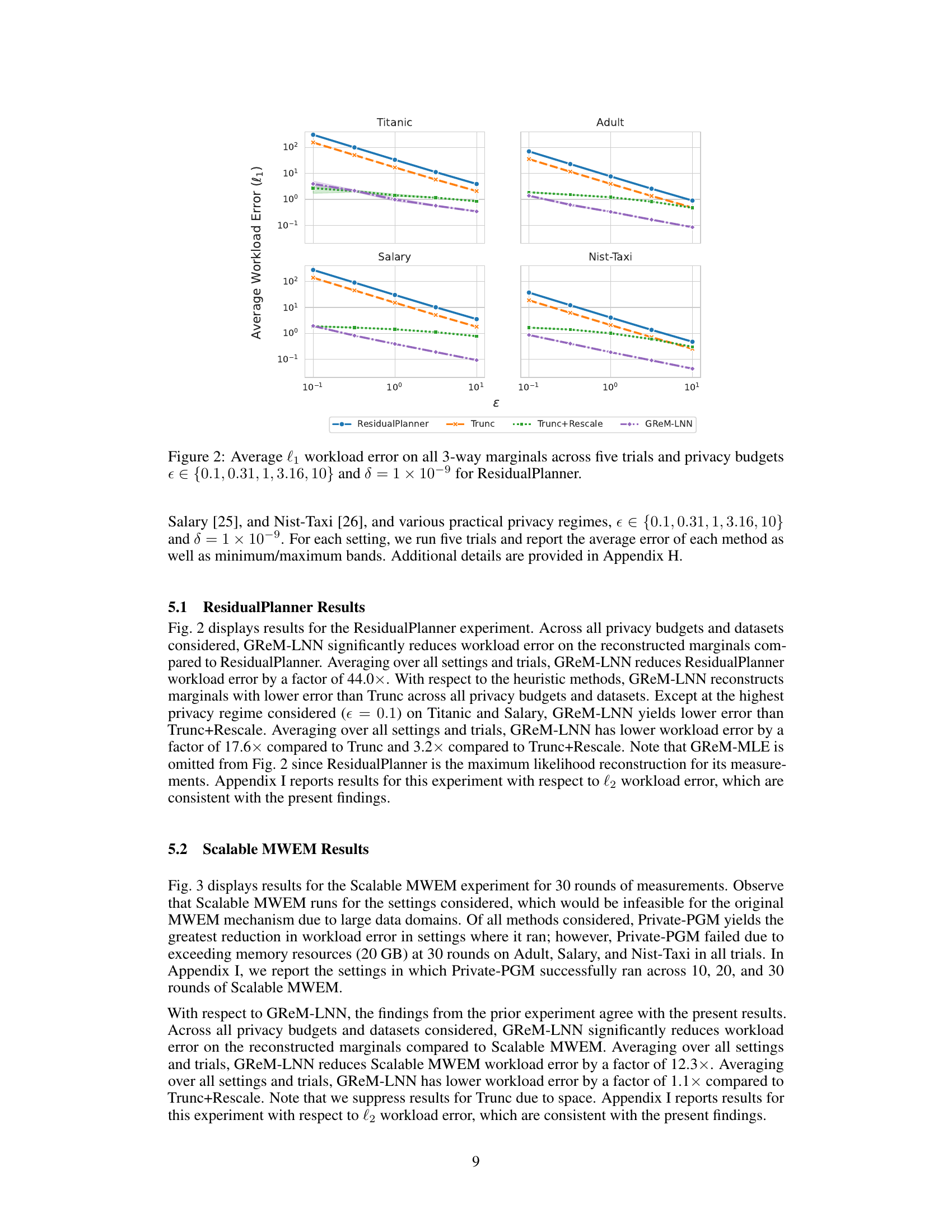
🔼 This figure displays the average l₁ workload error for all 3-way marginals across five trials. The experiments were conducted using different privacy budgets (ε) ranging from 0.1 to 10, with δ fixed at 1 × 10⁻⁹. The results are shown for the ResidualPlanner algorithm and three comparative methods: Trunc, Trunc+Rescale, and GReM-LNN. Each line represents a method, showing how the average error changes with varying privacy budget. This visualization helps to compare the performance of these methods under different privacy constraints.

read the caption

Figure 2: Average l₁ workload error on all 3-way marginals across five trials and privacy budgets ∈ {0.1, 0.31, 1, 3.16, 10} and δ = 1 × 10⁻⁹ for ResidualPlanner.

🔼 This table summarizes the time complexity of three different methods for reconstructing answers to marginal queries: GReM-MLE, EMP, and one round of GReM-LNN. The running time for each method is expressed using Big O notation and depends on the size of the marginal workload W, the set of measured residuals S, and the number of attributes in each marginal query.

read the caption

Table 1: Summary of Complexity Results

In-depth insights

#

Private Marginal Reconstruction

#

Private marginal reconstruction, a crucial aspect of differentially private data release, focuses on accurately reconstructing marginal distributions from noisy query responses while preserving privacy. The challenge lies in balancing utility (accuracy of reconstruction) and privacy (limiting information leakage). Effective reconstruction methods leverage the inherent structure of marginal queries, often employing techniques like pseudoinversion of carefully chosen query matrices or optimization algorithms to minimize reconstruction error. Local non-negativity constraints, enforcing the inherent non-negativity of marginal probabilities, further improve accuracy. The efficiency of these methods is critical for scalability to high-dimensional datasets, necessitating the use of computationally efficient algorithms and compact data representations. This is further complicated by the need to optimize the selection of queries for measurement, a key component of the overall privacy-preserving query release pipeline, to balance the trade-off between privacy budget and accuracy. Therefore, private marginal reconstruction is a complex area requiring advanced techniques in linear algebra, optimization, and differential privacy to achieve optimal results.

ReM Algorithm

#

The ReM (Residuals-to-Marginals) algorithm offers a principled and efficient approach to reconstruct marginal query answers from noisy residual measurements. Its key innovation lies in leveraging the inherent structure and relationships between marginals and residuals, specifically their orthogonal properties and compact Kronecker product representations. This allows ReM to avoid the computational burden associated with directly reconstructing high-dimensional data distributions, a significant hurdle for many existing methods. By using the pseudoinverse of a residual query basis, ReM efficiently maps noisy residual measurements onto the space of marginal queries. ReM’s flexibility allows it to be applied with various query answering mechanisms and noise distributions, making it a versatile tool for improving the accuracy and scalability of private data release. The algorithm’s efficiency stems from its use of fast pseudoinverse calculations within this compact representation, and its adaptability opens doors for further optimization and enhancements. A notable extension, GReM-LNN, adds local non-negativity constraints to further refine the reconstruction process, yielding more accurate and practically useful results. The demonstrated improvements in error reduction and scalability highlight ReM’s potential as a key component in advanced differentially private query answering systems.

GReM-LNN

#

GReM-LNN, an extension of the ReM (Residuals-to-Marginals) method, presents a principled approach to reconstructing marginal queries while enforcing local non-negativity. This constraint significantly improves the accuracy of the reconstructed marginals, aligning them with the inherent non-negative nature of real-world datasets. The method leverages the efficient pseudoinversion of residual query matrices, avoiding the computational burden of high-dimensional datasets while maintaining the accuracy of the results. Local non-negativity is particularly valuable when dealing with data containing frequencies or counts, and it is enforced during the reconstruction phase instead of as a separate post-processing step, leading to improved results. GReM-LNN’s efficiency and scalability are highlighted by its use of Kronecker product structures, enabling rapid computation and making it suitable for high-dimensional data. While GReM-LNN improves upon existing techniques, its heuristic weighting scheme is an area for further research, particularly concerning the balance between lower and higher degree residuals and the relationship between weights in the loss function and overall reconstruction quality.

Empirical Studies

#

An Empirical Studies section in a research paper on differentially private marginal reconstruction would ideally present a robust evaluation of the proposed methods (ReM and GReM-LNN). This would involve comparing their performance against existing state-of-the-art techniques on diverse real-world datasets, varying in size and dimensionality. Key metrics to report would include accuracy (e.g., L1, L2 error) and efficiency (runtime), potentially broken down by query type and dataset characteristics. The experiments should systematically explore the impact of different privacy parameters (epsilon and delta) on the overall performance, and also investigate the effect of non-negativity constraints. A detailed description of the experimental setup, including data preprocessing and parameter choices, is crucial for reproducibility. Finally, a thorough statistical analysis (e.g., hypothesis tests, confidence intervals) is essential to validate the significance of observed differences in performance between methods. The results should be presented in a clear and understandable format, preferably with visualizations to showcase trends and insights effectively. Ideally, the study also addresses any potential challenges encountered during experimentation and discusses the limitations of the experimental evaluation.

Future Works

#

The paper’s ‘Future Works’ section would benefit from expanding on several key areas. Addressing fairness concerns in privacy-preserving data analysis is crucial, as current methods may lead to biased outcomes. Investigating this thoroughly and proposing mitigation strategies would be impactful. The weighting scheme used in GReM-LNN for local non-negativity needs further exploration to understand its impact on reconstruction accuracy and convergence. Investigating alternative weighting schemes and establishing a theoretical understanding of their performance would enhance the method’s robustness and applicability. Extending ReM and GReM-LNN to handle continuous data is a critical next step, potentially via effective discretization techniques. Finally, a comprehensive analysis of the relationship between residual weights, optimization convergence, and reconstruction quality is needed to provide deeper insights into the algorithm’s behavior and enable better parameter tuning.

More visual insights

#

More on figures

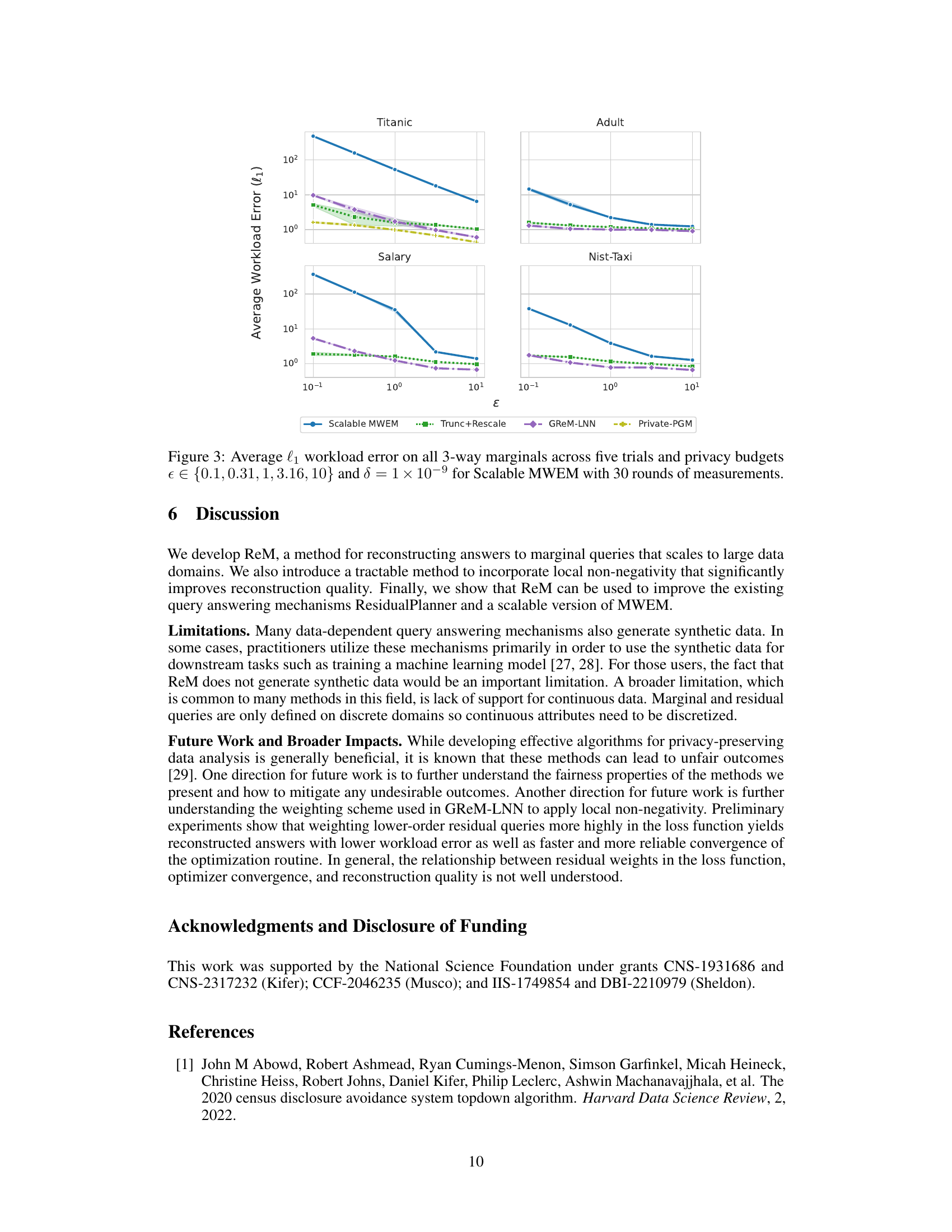
🔼 The figure shows the average l1 workload error for all 3-way marginals across five trials for four different datasets (Titanic, Adult, Salary, Nist-Taxi). The x-axis represents the privacy parameter epsilon (ε), and the y-axis shows the average l1 workload error. Multiple methods are compared: Scalable MWEM, Trunc+Rescale, GReM-LNN, and Private-PGM. The results indicate the performance of these methods under various privacy settings for reconstructing marginals, showing the effectiveness of GReM-LNN in reducing error.

read the caption

Figure 3: Average l₁ workload error on all 3-way marginals across five trials and privacy budgets ∈ {0.1, 0.31, 1, 3.16, 10} and δ = 1 × 10−9 for Scalable MWEM with 30 rounds of measurements.

🔼 This figure compares the average l2 workload error of different methods for reconstructing 3-way marginal queries across four datasets (Titanic, Adult, Salary, Nist-Taxi) and five privacy budgets (ε). The methods compared are ResidualPlanner, Trunc, Trunc+Rescale, and GReM-LNN. Each data point represents the average l2 error over five trials. The figure shows that GReM-LNN generally outperforms other methods, especially at higher privacy budgets.

read the caption

Figure 4: Average l2 workload error on all 3-way marginals across five trials and privacy budgets ∈ {0.1, 0.31, 1, 3.16, 10} and δ = 1 × 10−9 for ResidualPlanner.

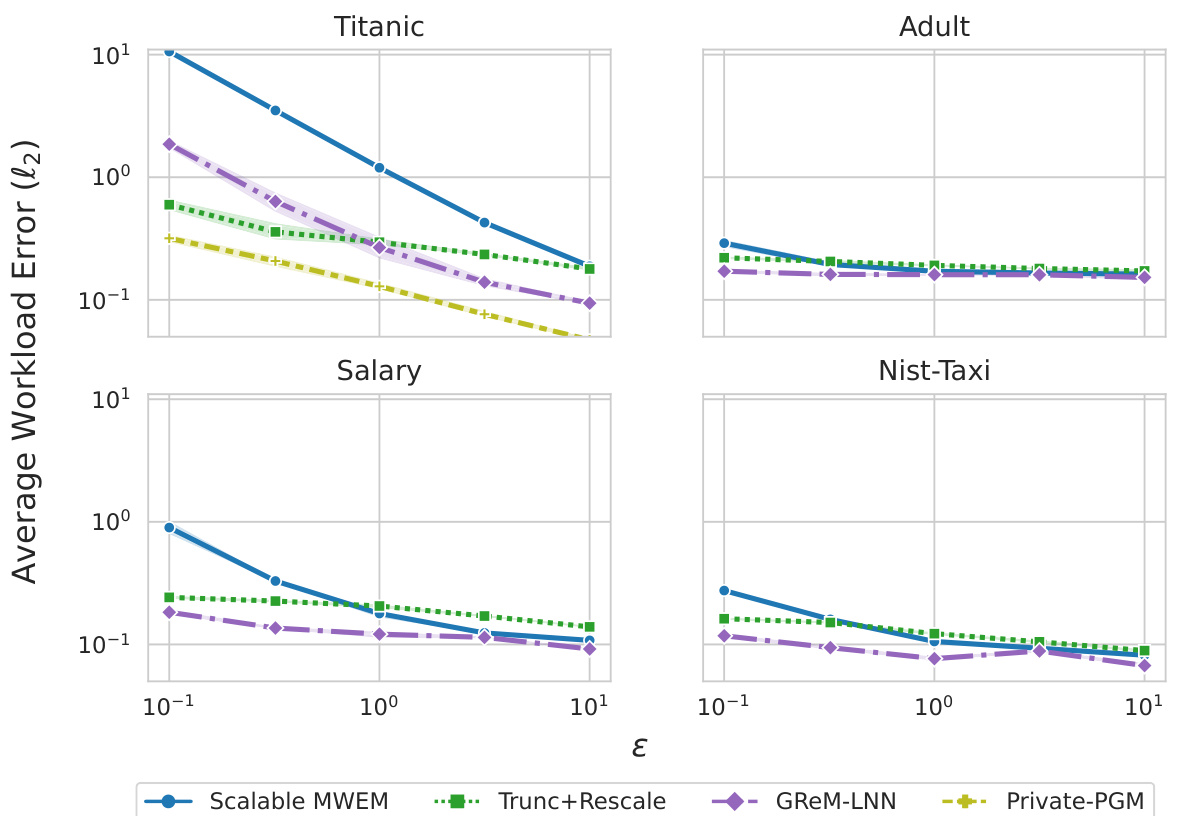
🔼 The figure shows the average l2 workload error for all 3-way marginals across five trials for different privacy budgets (ε) and using Scalable MWEM with 30 rounds of measurements. It compares the performance of four methods: Scalable MWEM, Trunc+Rescale, GReM-LNN, and Private-PGM on four different datasets: Titanic, Adult, Salary, and Nist-Taxi. The x-axis represents the privacy parameter (ε), and the y-axis represents the average workload error (l2).

read the caption

Figure 5: Average l2 workload error on all 3-way marginals across five trials and privacy budgets ∈ {0.1, 0.31, 1, 3.16, 10} and δ = 1 × 10−9 for Scalable MWEM with 30 rounds of measurements.

More on tables

🔼 This table summarizes the time complexity of three different methods for reconstructing answers to marginal queries: GReM-MLE, EMP, and one round of GReM-LNN. The complexity is expressed in Big O notation and depends on the size of the marginal workload (W), the set of measured residuals (S), and the size of the measured residuals (z). The table shows that the running time of all three methods is nearly linear in the size of the data domain.

read the caption

Table 1: Summary of Complexity Results

🔼 This table summarizes the time complexity of three different marginal reconstruction methods: GReM-MLE, EMP, and one round of GReM-LNN. The complexity is expressed in Big O notation and depends on the size of the marginal workload (W), the set of measured residuals (S), and the size of the measured residuals for each attribute subset (n). The table shows that the time complexity of all three methods is almost linear with respect to the size of the domain, which is a significant improvement over existing methods.

read the caption

Table 1: Summary of Complexity Results

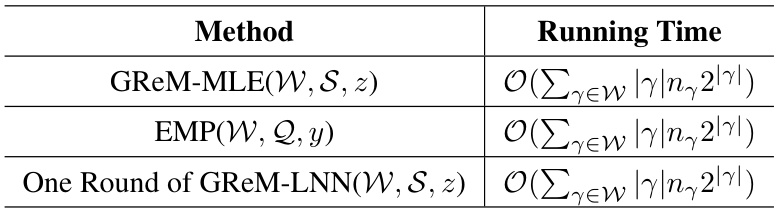
🔼 This table summarizes the time complexity of three different methods for reconstructing answers to marginal queries: GReM-MLE, EMP, and one round of GReM-LNN. The time complexity is expressed in big O notation and depends on the size of the marginal workload W and the number of residuals in the measurement sets S or Q. The table shows that all three methods have a similar time complexity, which is nearly linear in the size of the data domain.

read the caption

Table 1: Summary of Complexity Results

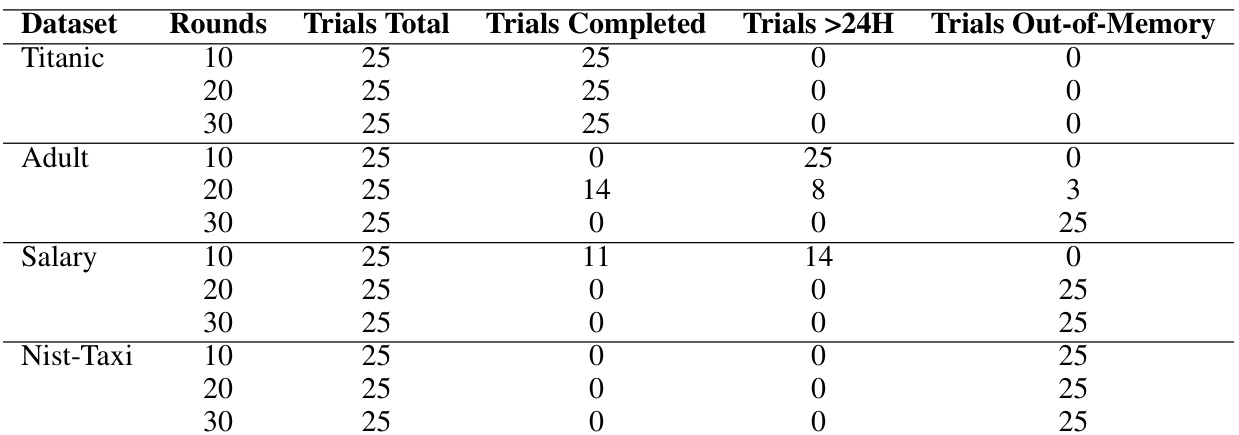
🔼 This table shows the results of running the Private-PGM algorithm within the Scalable MWEM experiment across different datasets and numbers of rounds. It details the number of trials that completed successfully, exceeded the 24-hour time limit, or ran out of memory (20GB).

read the caption

Table 2: Completion results of running Private-PGM by setting for the Scalable MWEM experiment. Failure is broken down by exceeding the 24H time limit or exceeding the available memory (20GB).

Full paper

#