TL;DR#
Large Language Models (LLMs) are growing rapidly in size, making them difficult and expensive to deploy on devices with limited resources. Existing compression techniques often struggle to balance compression ratios with maintaining model performance, especially in low-bit quantization regimes. This necessitates the development of new methods to effectively compress LLMs without significant performance degradation.
This paper introduces CALDERA, a novel post-training LLM compression algorithm that addresses this challenge. CALDERA uses a low-rank, low-precision decomposition to approximate the weight matrices of LLMs. The method is theoretically analyzed, providing error bounds, and empirically evaluated on several LLMs, demonstrating significant improvements over existing techniques, particularly in the low-bit quantization regime (less than 2.5 bits per parameter). The algorithm also demonstrates adaptability to existing low-rank adaptation techniques, further boosting performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on LLM compression and post-training quantization. It introduces a novel algorithm, outperforming existing methods in compressing large language models with less than 2.5 bits per parameter. This opens new avenues for deploying LLMs on resource-constrained devices, a critical challenge in the field. The theoretical analysis provides strong guarantees, adding rigor to the empirical results.
Visual Insights#

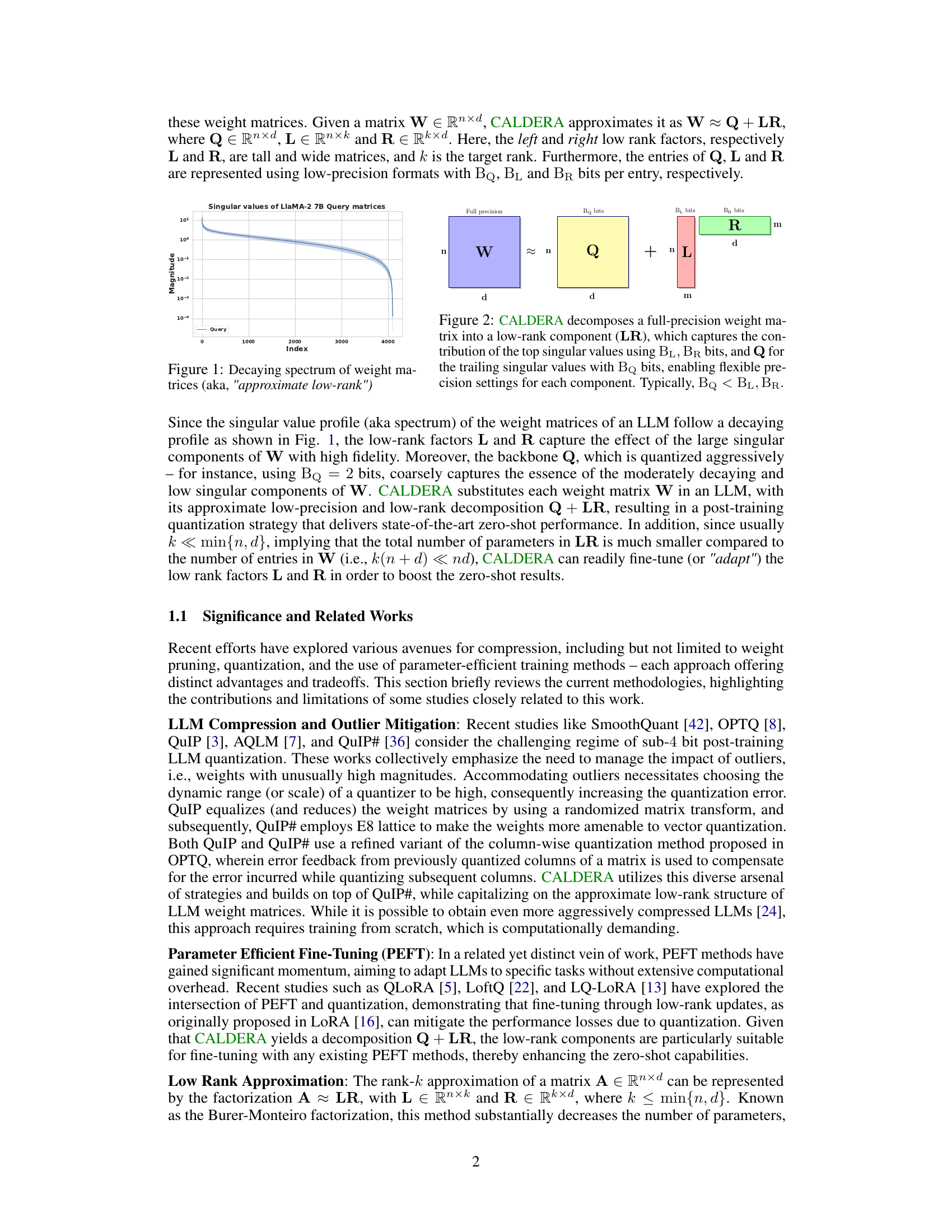
🔼 This figure shows the decaying singular value profile of the weight matrices in a Llama-2 7B Query model. The y-axis represents the magnitude of the singular values, and the x-axis represents their index (rank). The plot demonstrates that a significant portion of the singular values have low magnitude, indicating an inherent low-rank structure in the weight matrices. This low-rank property is exploited by CALDERA for model compression.
read the caption
Figure 1: Decaying spectrum of weight matrices (aka, 'approximate low-rank')
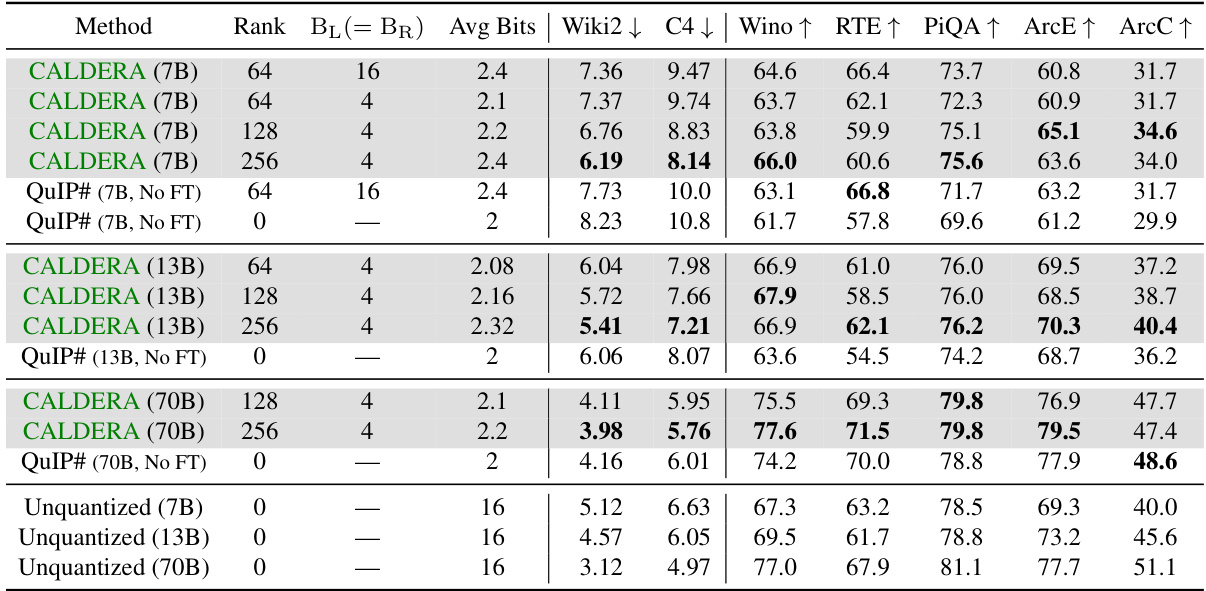
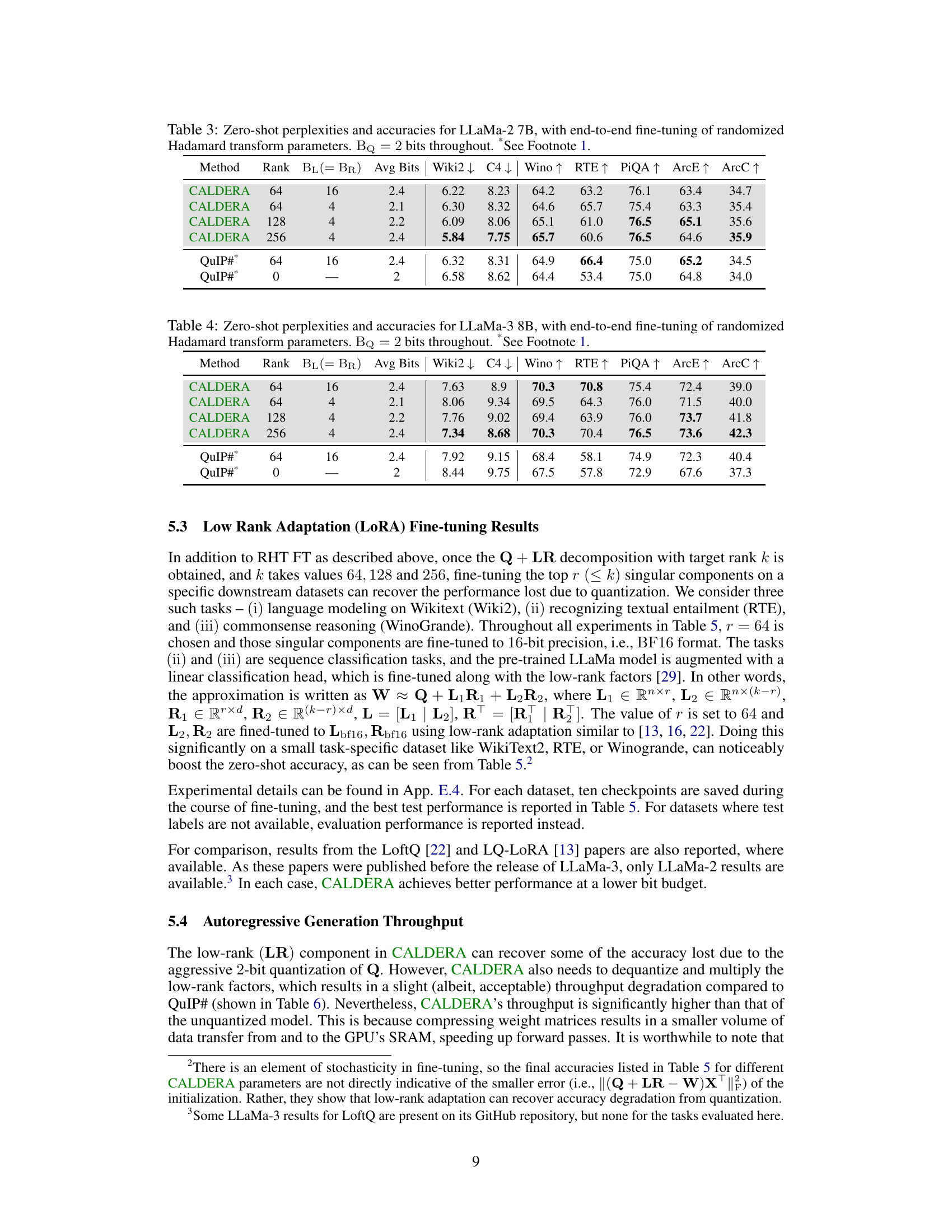
🔼 This table presents the zero-shot performance results for the LLaMa-2 model (7B, 13B, and 70B parameters) after applying the CALDERA compression algorithm. It compares the performance of CALDERA with different rank (k) values of low-rank factors (L and R) against QuIP# baselines (with and without fine-tuning) and the original unquantized model. The evaluation metrics include perplexity on WikiText2 and C4 datasets, as well as zero-shot accuracy on several tasks (Winogrande, RTE, PiQA, ARC-Easy, and ARC-Challenge). The ‘Avg Bits’ column represents the average number of bits used per parameter in the compressed model.
read the caption
Table 1: Zero-shot perplexities (denoted by ↓) and accuracies (↑) for LLaMa-2. BQ = 2 bits throughout.
In-depth insights#
LLM Low-Rank#
The concept of “LLM Low-Rank” centers on the observation that the massive weight matrices within Large Language Models (LLMs) often exhibit redundancy, meaning they possess a low-rank structure. This low-rank property implies that a significant portion of the information in these matrices is captured by a smaller number of underlying factors. Exploiting this low-rank structure is crucial for LLM compression because it allows for approximating the large matrices using much smaller representations, thereby reducing model size, memory footprint, and computational cost during inference. Various techniques, such as matrix factorization and dimensionality reduction methods, can be employed to identify and leverage this low-rank structure. The core idea is to represent the original high-dimensional weight matrices with lower-rank approximations, while striving to minimize the information loss and maintaining model performance. This is a key area of research in efficient LLM deployment and optimization, focusing on striking a balance between model compression and preserving the quality of generated text. Furthermore, the effectiveness of low-rank approaches strongly depends on the specific LLM architecture and training data.
CALDERA Algorithm#
The CALDERA algorithm is a novel post-training compression technique for Large Language Models (LLMs). It leverages the inherent low-rank structure of LLM weight matrices, approximating them as a sum of a low-rank component and a low-precision component. This decomposition (W ≈ Q + LR) allows for significant compression by reducing the number of parameters and using lower precision representations. Calibration data is used to minimize the approximation error, ensuring minimal performance degradation after compression. A key innovation is the algorithm’s ability to efficiently handle the quantization of all three components (Q, L, and R). Theoretical guarantees on the approximation error are provided. CALDERA’s effectiveness is demonstrated through experiments on several LLMs, showcasing superior performance to existing methods, particularly in the low bit-per-parameter regime. The algorithm also facilitates low-rank adaptation, enabling further performance improvements through fine-tuning.
Quant. Error Bounds#
Analyzing quantization error bounds is crucial for understanding the trade-offs in model compression. Tight bounds provide confidence in the performance of a compressed model, while loose bounds may indicate limitations or the need for further analysis. The theoretical analysis often involves probabilistic arguments and assumptions about the data distribution and quantization scheme. Key considerations in the analysis include the bit-depth of quantization, the properties of the quantizer (e.g., uniform, non-uniform), and the impact of outliers. The analytical framework might leverage techniques from linear algebra, probability theory, and information theory. A robust analysis should also address the impact of model architecture, training data, and task complexity on the overall quantization error. Ultimately, quantifiable error bounds are vital for ensuring a compressed model’s reliability and accuracy, and their development necessitates a solid theoretical foundation complemented by rigorous empirical evaluation.
Zero-Shot Results#
The ‘Zero-Shot Results’ section is crucial for evaluating the effectiveness of CALDERA, a novel LLM compression algorithm. It assesses the model’s performance without any fine-tuning on downstream tasks, reflecting its inherent capability after compression. The results, presented in tables, show perplexity scores (lower is better) and zero-shot accuracy across various benchmarks. Key insights likely include the impact of different compression ratios (controlled by rank and bit-budget), showing the tradeoff between compression and performance. Comparing CALDERA’s performance to baselines (e.g., uncompressed models, QuIP#) highlights its advantages, particularly in the low-bit regime. Analysis of the results would likely indicate the optimal balance between compression and accuracy, as well as revealing the strengths and weaknesses of CALDERA in different tasks. The presence of varying ranks (of low-rank factors L and R) and bit-budgets would provide a comprehensive evaluation of the algorithm’s robustness.
Future Works#
Future research directions stemming from this LLM compression work are plentiful. Improving the theoretical bounds on approximation error is crucial, potentially through refinements of the rank-constrained regression framework or exploration of alternative optimization techniques. Investigating the interaction between quantization and low-rank approximation more deeply could lead to even more efficient compression strategies. The current approach uses a heuristic for updating the Hessian matrix; a rigorous analysis of this heuristic and the exploration of alternative methods is warranted. Expanding the range of LLMs tested and further evaluating performance on diverse downstream tasks is important. Exploring the integration of CALDERA with existing parameter-efficient fine-tuning methods could potentially yield substantial improvements in zero-shot and few-shot learning scenarios. Lastly, research on the computational efficiency is necessary; optimizations such as custom kernels and more sophisticated quantization techniques could significantly boost throughput.
More visual insights#
More on figures
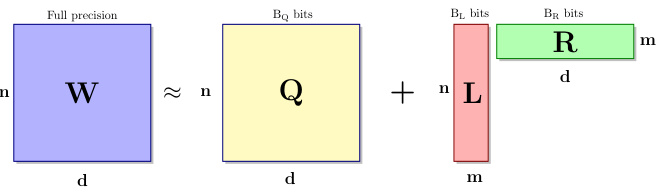
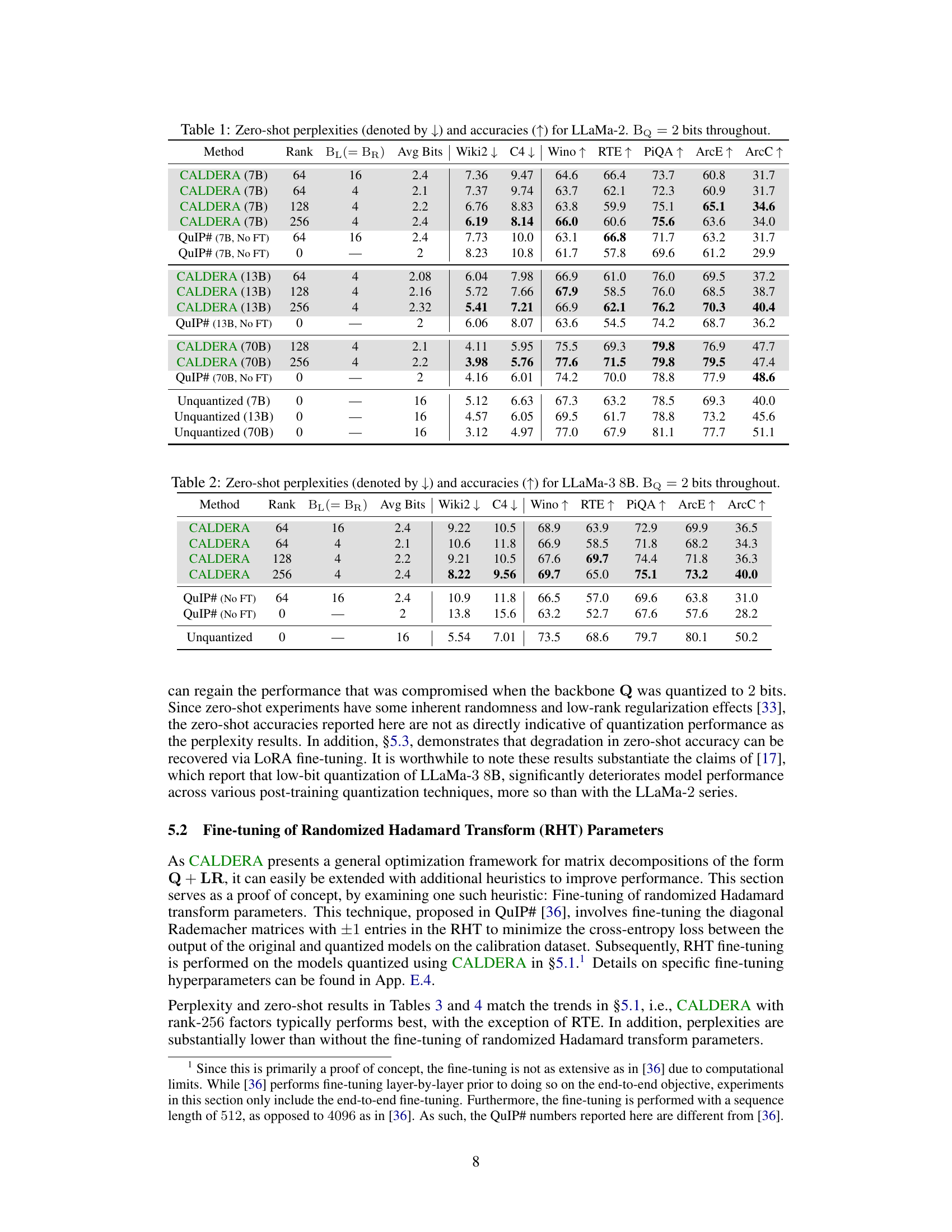
🔼 The figure shows how CALDERA decomposes a full-precision weight matrix (W) into three components: a low-rank component (LR) and a backbone (Q). The low-rank component captures the most significant singular values of the matrix with higher precision (using BL and BR bits), while the backbone captures the remaining, less significant singular values with lower precision (BQ bits). This decomposition allows for flexible precision settings and compression of the model.
read the caption
Figure 2: CALDERA decomposes a full-precision weight matrix into a low-rank component (LR), which captures the contribution of the top singular values using BL, BR bits, and Q for the trailing singular values with BQ bits, enabling flexible precision settings for each component. Typically, BQ < BL, BR.
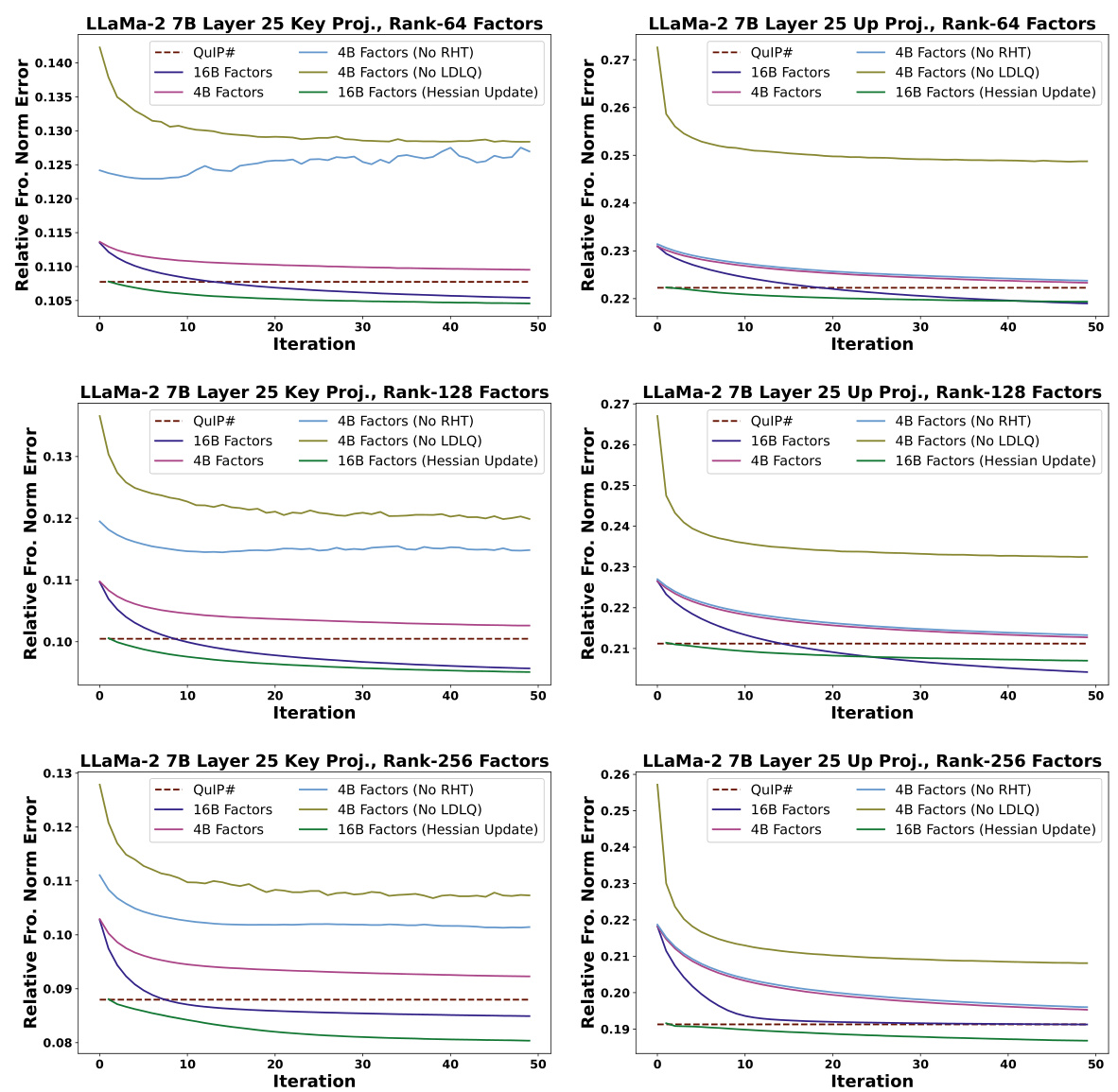
🔼 This figure shows the relative Frobenius norm error per iteration for several variants of the CALDERA algorithm and the QuIP# algorithm. Different lines represent different configurations of CALDERA (e.g., 4-bit factors, 16-bit factors, with/without Hessian update, with/without randomized Hadamard transform). The results show the convergence behavior of the various methods for different low-rank sizes (64, 128, and 256).
read the caption
Figure 3: Relative data-aware Frobenius norm error per iteration of CALDERA for selected matrices of LLaMa-2 7B layer 25. For all experiments, the bit precision of Q is 2, and the calibration dataset is the same as used in §5. The first iteration of CALDERA with the Hessian update is omitted, as it has a large error, inhibiting plot readability.
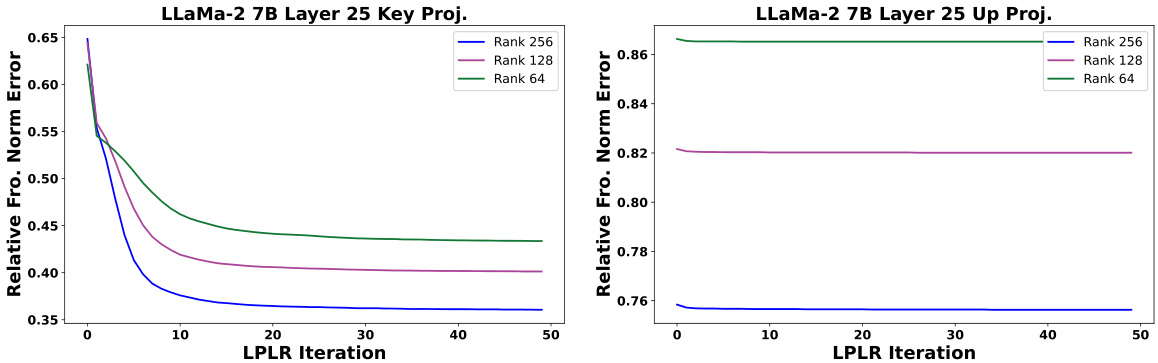
🔼 This figure shows the convergence of the LPLRFACTORIZE algorithm for two weight matrices in the 25th layer of the LLaMa-2 7B model. The plots illustrate the relative data-aware Frobenius norm error at each iteration of the algorithm, for different target ranks (64, 128, 256). The randomized Hadamard transform was applied to the weight matrices before factorization, and both low-rank factors were quantized to 4 bits using an E8 lattice quantizer. The figure demonstrates that the alternating minimization steps in the algorithm effectively reduce the approximation error, although the degree of improvement varies depending on the weight matrix and the target rank.
read the caption
Figure 4: Relative data-aware Frobenius norm error per iteration of LPLRFACTORIZE, for the decomposition W ≈ LR, for two matrices in LLaMa-2 7B layer 25.
More on tables
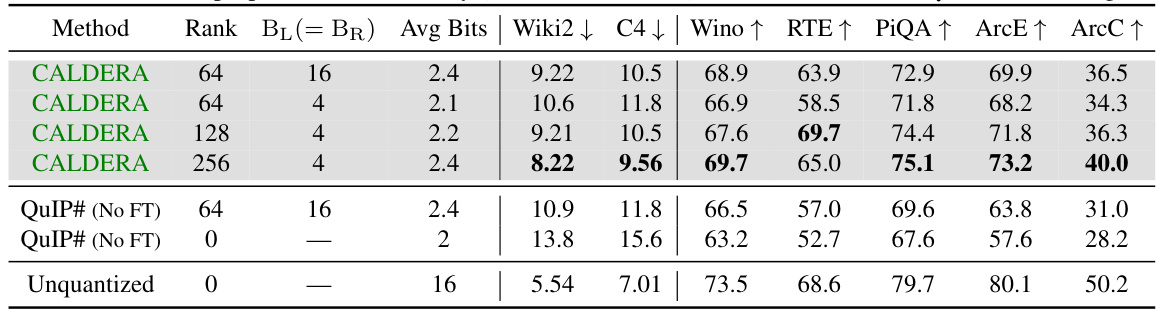
🔼 This table presents the results of zero-shot evaluations on the LLaMa-3 8B model after applying different compression methods. It compares CALDERA with different rank values (64, 128, 256) and bit configurations for low-rank factors (4-bit and 16-bit) against QuIP# (without fine-tuning) and the uncompressed baseline. The evaluation metrics include perplexity on Wiki2 and C4 datasets, and zero-shot accuracy on Winogrande, RTE, PiQA, ArcE, and ArcC tasks. Lower perplexity values and higher accuracy percentages indicate better performance.
read the caption
Table 2: Zero-shot perplexities (denoted by ↓) and accuracies (↑) for LLaMa-3 8B. BQ = 2 bits throughout.
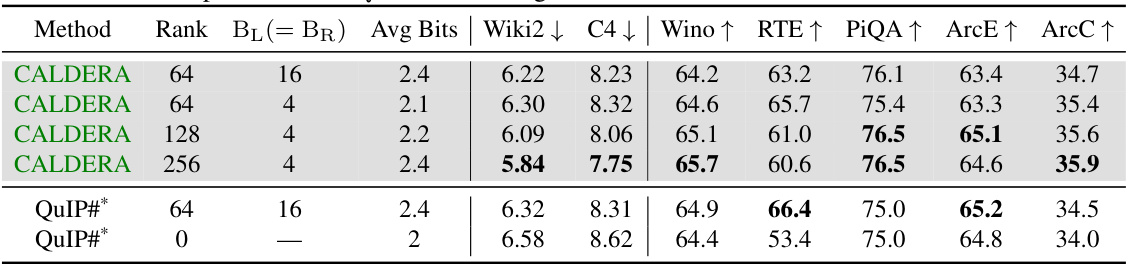
🔼 The table presents zero-shot perplexity and accuracy results on various tasks for Llama-2 7B model after applying CALDERA with different parameter settings. It compares the results to QuIP# baselines with and without fine-tuning, and also shows unquantized results. It highlights the impact of varying target rank, bit precision of low rank factors, and whether or not randomized Hadamard transform parameter fine-tuning is employed. Lower perplexity is better; higher accuracy is better.
read the caption
Table 3: Zero-shot perplexities and accuracies for LLaMa-2 7B, with end-to-end fine-tuning of randomized Hadamard transform parameters. BQ = 2 bits throughout. *See Footnote 1.
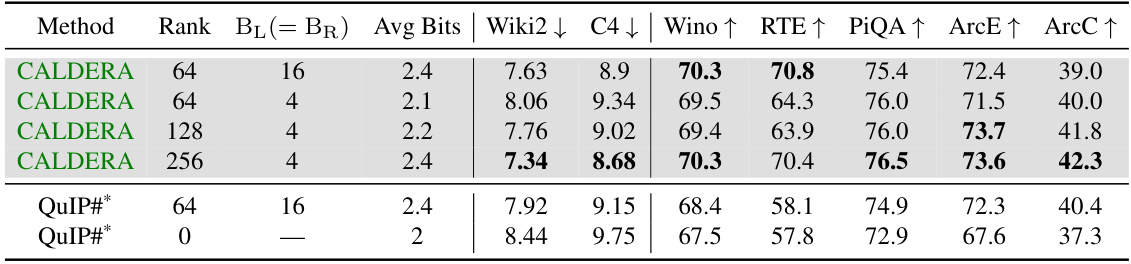
🔼 This table presents the results of zero-shot experiments conducted on the LLaMa-3 8B model. The experiments involved quantizing the model using different configurations of the CALDERA algorithm, varying the rank of the low-rank factors (L and R) and their bit precision. The table reports perplexity scores (lower is better) and zero-shot accuracies (higher is better) on several downstream tasks, including language modeling (Wiki2 and C4) and commonsense reasoning (Winogrande, RTE, PiQA, ArcE, ArcC). Results for QuIP# (without fine-tuning) are included for comparison, demonstrating the effectiveness of CALDERA’s low-rank and low-precision approach.
read the caption
Table 2: Zero-shot perplexities (denoted by ↓) and accuracies (↑) for LLaMa-3 8B. BQ = 2 bits throughout.
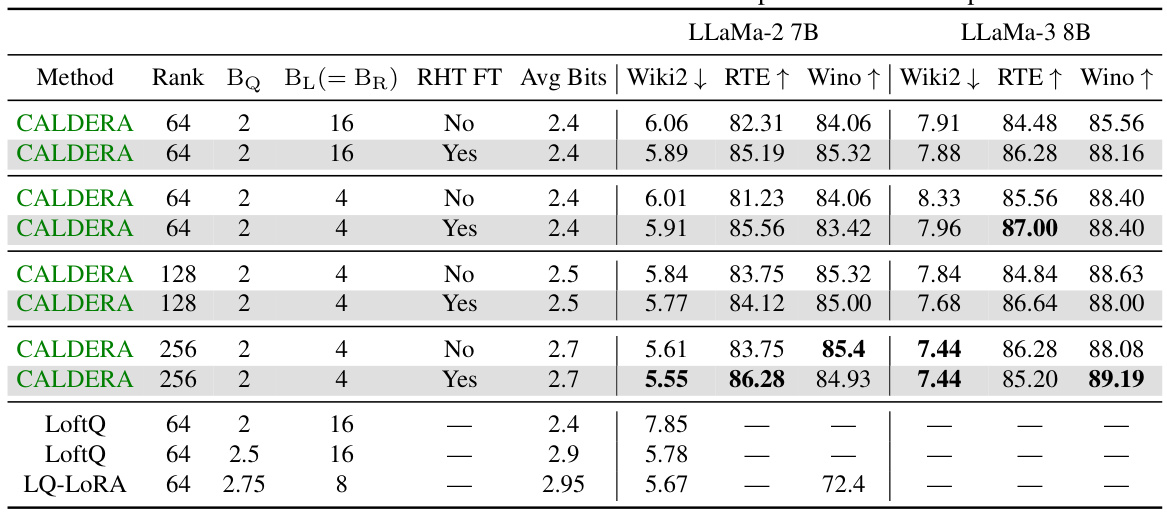
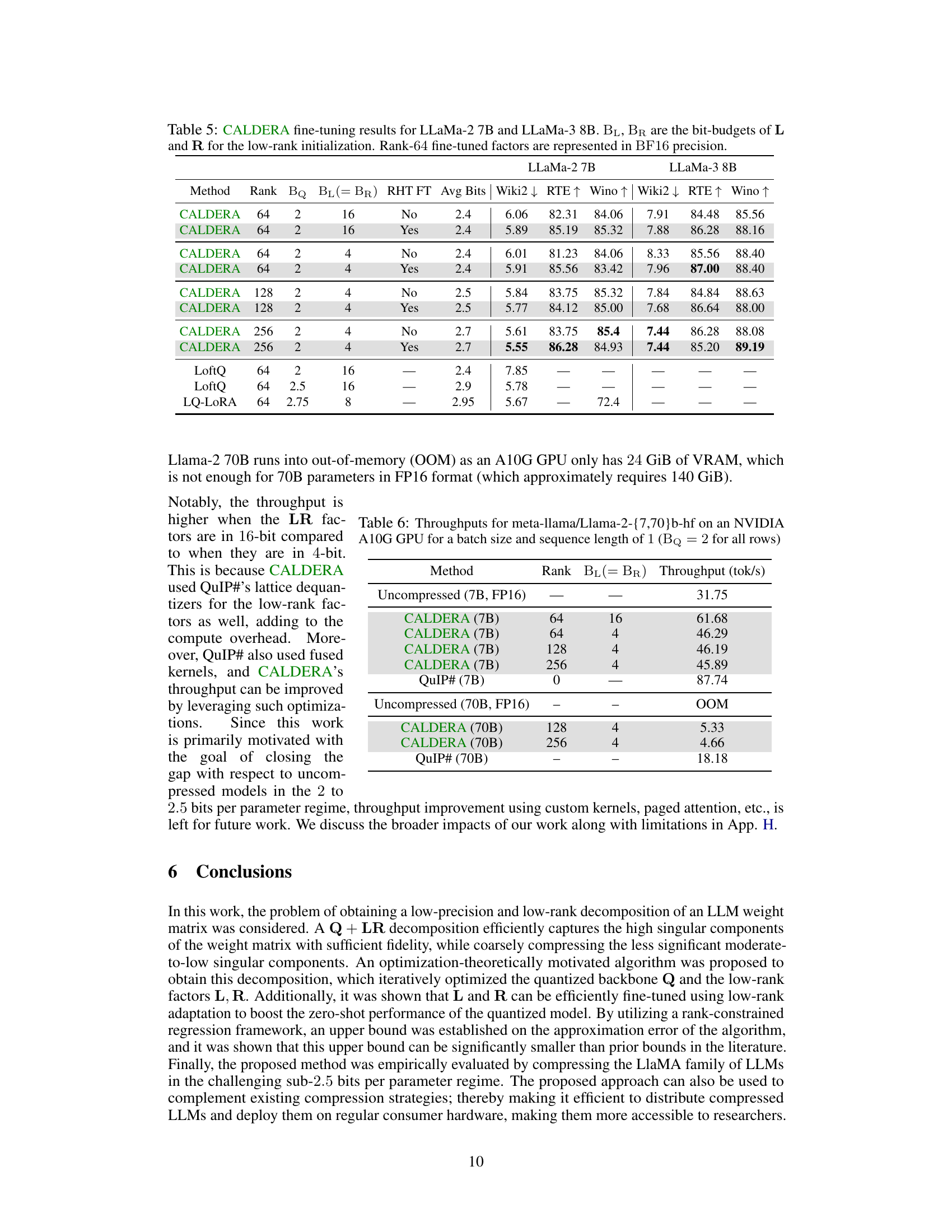
🔼 The table presents the results of zero-shot experiments on the LLaMa-2 model (7B, 13B, and 70B parameters) after applying the CALDERA algorithm with different compression parameters. It compares CALDERA’s performance against QuIP# (without fine-tuning) as a baseline. The metrics used include perplexity on the Wiki2 and C4 datasets, and zero-shot accuracy on Winogrande, RTE, PiQA, ARC-Easy, and ARC-Challenge datasets. The table shows perplexity (lower is better) and accuracy (higher is better) for various model sizes and hyperparameter settings (rank and bit budget for the low-rank components).
read the caption
Table 1: Zero-shot perplexities (denoted by ↓) and accuracies (↑) for LLaMa-2. BQ = 2 bits throughout.
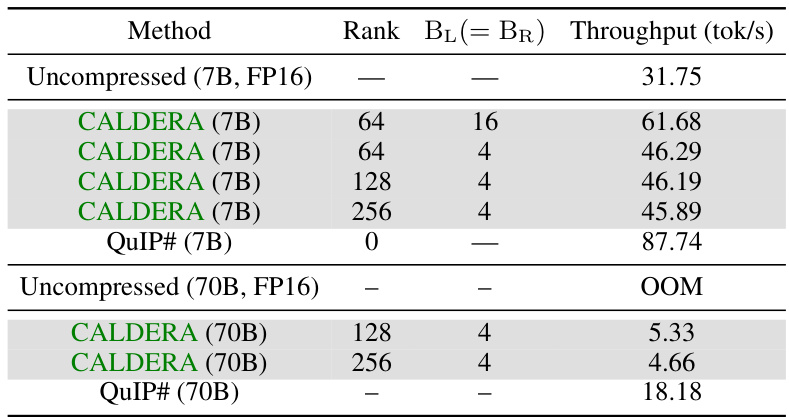
🔼 This table presents the throughput, measured in tokens per second, for different LLM compression methods using an NVIDIA A10G GPU. The throughput is compared for the uncompressed LLMs (Llama-2 7B and 70B), CALDERA with different rank and bit-depth configurations, and QuIP#. The batch size and sequence length are fixed at 1, and the number of bits for the backbone (Q) is consistently 2 for all experiments.
read the caption
Table 6: Throughputs for meta-llama/Llama-2-{7,70}b-hf on an NVIDIA A10G GPU for a batch size and sequence length of 1 (Bq = 2 for all rows)
🔼 This table presents the zero-shot perplexity and accuracy results for the LLaMa-2 model (7B, 13B, and 70B parameters) compressed using CALDERA. It shows the impact of different parameters (rank, bit-budget) on the performance of the compressed model compared to QuIP# (with and without fine-tuning). Lower perplexity indicates better performance. The results are reported for the Wiki2 and C4 datasets, as well as for Winogrande, RTE, PiQA, ARC-Easy, and ARC-Challenge tasks.
read the caption
Table 1: Zero-shot perplexities (denoted by ↓) and accuracies (↑) for LLaMa-2. BQ = 2 bits throughout.

🔼 This table shows the hyperparameter settings used for low-rank adaptation fine-tuning experiments. It details the dataset used, block size, batch size (per device), gradient accumulation steps, number of epochs, learning rate, weight decay, learning rate scheduler, and warmup steps for three different tasks: Wikitext2, RTE, and Winogrande. The asterisk indicates that additional details are available elsewhere in the paper.
read the caption
Table 8: Hyperparameter settings for low-rank adaptation*. Batch size refers to the per-device batch size. All fine-tuning experiments are parallelized across four GPUs.

🔼 This table shows the performance comparison between CALDERA and QuIP# methods on Mistral 7B model for various tasks. The performance metrics include perplexity scores on WikiText2 and C4 datasets, and zero-shot accuracies on Winograd Schema Challenge, Physical Interaction Question Answering, ARC-Easy, and ARC-Challenge datasets. Both methods use calibration datasets from HuggingFace and have 2-bit quantization for the backbone. However, CALDERA further uses 4-bit quantization for low-rank factors. The table demonstrates that CALDERA achieves lower perplexity and generally higher accuracies than QuIP#.
read the caption
Table 9: Evaluations of Wikitext2 and C4 perplexities, as well as percent accuracies on some common language modeling benchmarks, on CALDERA-compressed Mistral 7B. All quantizations use calibration datasets released on Huggingface by the authors of QuIP#. BQ = 2 bits throughout, and BL = BR = 4 bits where low-rank factors are present. For fairness of comparison, QuIP# numbers reported do not include RHT finetuning.
Full paper#