↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Approximate Natural Gradient Descent (NGD) methods, while popular, suffer from the limitations of Empirical Fisher (EF) approximation, notably its poor approximation quality. This is due to an inversely-scaled projection issue that biases updates towards already well-trained samples. This issue hinders efficient training, requiring complicated step-size schedulers and significant damping to function effectively.
This paper introduces the Improved Empirical Fisher (iEF) method to overcome this. iEF is presented as a generalized NGD method that addresses the projection issue while maintaining the practicality of EF. Through extensive experimentation, iEF demonstrates superior approximation quality and significantly better optimization performance in various deep learning tasks compared to both the EF and other methods. A novel empirical evaluation framework, specifically designed for large-scale tasks, is also presented to enable thorough benchmarking of approximate NGD methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning optimization because it addresses the limitations of existing empirical natural gradient descent methods. By proposing an improved empirical Fisher approximation, it paves the way for more robust and efficient training of large-scale deep learning models, thereby significantly impacting current research trends in parameter-efficient fine-tuning. The new evaluation framework enhances accuracy in comparing optimization algorithms. This work opens up new avenues for improving Fisher-based methods and optimizing convergence.
Visual Insights#

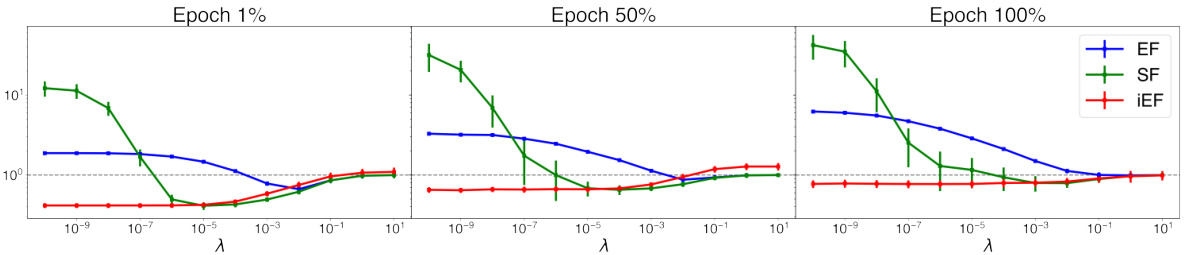
This figure compares the performance of three different optimization methods: SGD, NGD/iEF, and EF, on a simple 2-parameter, 2-data point linear least squares regression problem. The plots visualize the loss landscape, gradient vector fields, and training trajectories for each method. It highlights how the EF method suffers from an inversely scaled projection issue, leading to a distorted update vector field and inefficient training. In contrast, SGD and NGD/iEF efficiently converge to the global minimum.

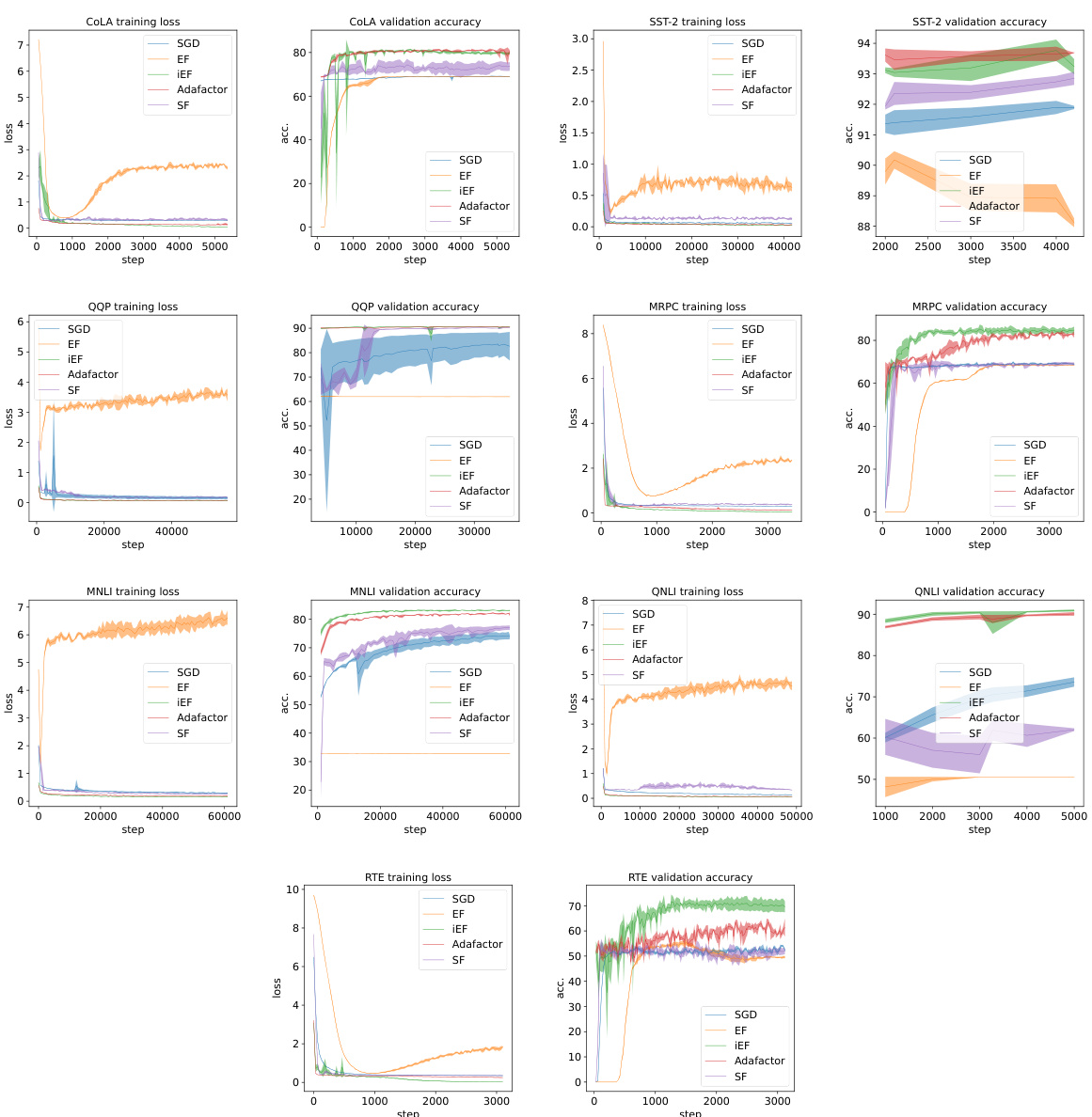
This table presents the average test performance results for different optimizers (AdamW, Adafactor, SGD, EF, SF, and iEF) across various tasks from the GLUE benchmark and CIFAR100. It summarizes the performance of each optimizer on these tasks by using average test metrics, considering both single and multiple metric scenarios and the best validation checkpoint for a comprehensive evaluation. Detailed results can be found in Table 7 of the paper.
In-depth insights#
Empirical Fisher Issue#
The empirical Fisher approximation, while computationally convenient for natural gradient descent, suffers from a significant limitation: inversely-scaled projection. This issue arises because the loss reduction enforced by EF updates is constant across all samples, regardless of their convergence level. Consequently, the method is easily biased towards well-trained samples, hindering efficient exploration of the parameter space. The inversely-scaled projection results in distorted update vector fields and inefficient training trajectories, often requiring sophisticated damping schemes to work effectively. This problem is particularly pronounced in large-scale setups where calculating the exact Fisher information matrix is computationally prohibitive, yet the limitations of the EF approximation become more apparent. An improved method is needed to overcome this deficiency, enabling better convergence and generalization in deep learning models. The paper proposes such a method, iEF, addressing this limitation while maintaining the simplicity of the EF approach.
Improved EF (iEF)#
The proposed iEF method addresses the limitations of the Empirical Fisher (EF) approximation used in Approximate Natural Gradient Descent (NGD) optimization. iEF improves EF’s approximation of the exact Fisher information matrix, a crucial component in NGD for accelerating training and enhancing generalization. The core issue with EF is identified as an inversely-scaled projection problem, where updates disproportionately favor well-trained samples. iEF mitigates this by introducing a diagonal scaling matrix, weighting updates based on sample convergence level. This generalized NGD approach, motivated by a loss reduction perspective, improves both convergence speed and generalization performance. Experimental results demonstrate iEF’s superior approximation quality to exact NG updates compared to both EF and computationally more expensive sampled Fisher methods. iEF’s robustness to the choice of damping parameter is a significant advantage, simplifying optimization and enhancing its practical utility.
iEF Evaluation#
The effectiveness of the improved empirical Fisher (iEF) approximation hinges on its ability to accurately reflect natural gradient (NG) updates, a key aspect addressed in the ‘iEF Evaluation’ section. A robust evaluation framework is crucial, assessing iEF’s approximation quality against both the standard empirical Fisher (EF) and the more computationally expensive sampled Fisher (SF) methods. This involves developing a novel metric, efficiently quantifiable within modern auto-differentiation frameworks, to directly measure the alignment of iEF updates with true NG updates. Large-scale experiments across diverse deep learning tasks (e.g., parameter-efficient fine-tuning of pre-trained models) become essential, validating not only the approximation quality but also the generalization and convergence performance of iEF when used as an optimizer. The robustness of iEF to the choice of damping parameter is another vital aspect, comparing its performance against EF and SF across multiple tasks and training stages. In essence, a strong ‘iEF Evaluation’ would rigorously demonstrate the superiority of iEF as both a more accurate approximation of the Fisher information matrix and a superior optimizer, showcasing its advantages over established methods in real-world deep learning applications.
iEF Applications#
The heading ‘iEF Applications’ suggests a section dedicated to exploring the practical uses of the Improved Empirical Fisher (iEF) method. It would likely detail how iEF can be leveraged in various contexts. One key application would be its direct use as an optimizer, potentially outperforming existing methods in terms of convergence speed and generalization ability. The section could demonstrate this superiority through experimental results on diverse machine learning tasks. Another crucial aspect would involve integrating iEF into existing approximate natural gradient descent (NGD) optimizers. This would show how iEF’s enhanced accuracy in approximating the Fisher information matrix can enhance the performance of these widely used optimizers. This integration might lead to improvements in convergence speed, robustness, and overall performance. A further application could center on iEF as an independent Fisher matrix approximation method, paving the way for advancements in other Fisher-based techniques that extend beyond optimization, such as model compression. The discussion might include illustrative examples and empirical evaluations showcasing the effectiveness of iEF across these varied applications. The section would conclude by summarizing the key advantages and potential impact of the proposed iEF method.
Future Work#
The authors suggest several promising avenues for future research. Improving existing approximate natural gradient descent (NGD) optimizers by integrating the improved empirical Fisher (iEF) method is a key direction. This would leverage iEF’s superior approximation quality and robustness while maintaining the efficiency of established optimizers like K-FAC. Exploring the application of iEF to other Fisher-based methods beyond optimization is another compelling area. This could lead to advancements in diverse tasks such as model compression and Hessian approximation. Further theoretical investigations into the iEF method’s convergence properties and their robustness to various loss functions and model architectures would provide a solid foundation for broader adoption and application. Finally, developing a more robust framework for evaluating the approximation quality of approximate NGD methods is vital. This would involve testing across a wider range of tasks and models to validate the generalizability of the current findings.
More visual insights#
More on figures

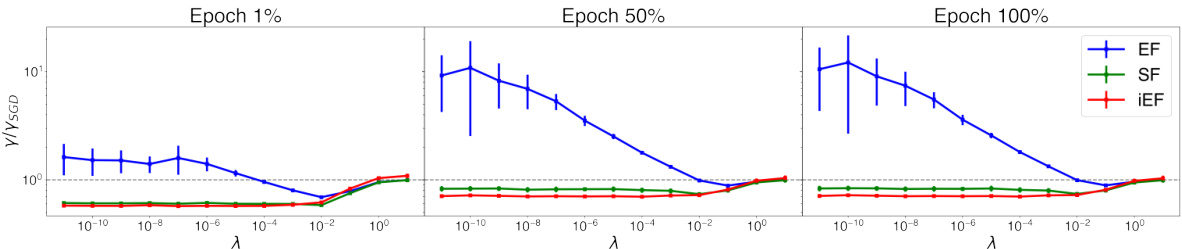
This figure compares the approximation quality of three different Fisher information matrix approximation methods (EF, iEF, and SF) against standard SGD. It shows the ratio of the approximation quality indicator (gamma) for each method relative to SGD across different training stages for three example tasks. It also shows the gradient norm imbalance across training epochs. The results indicate that iEF consistently provides a better approximation than EF and SF.
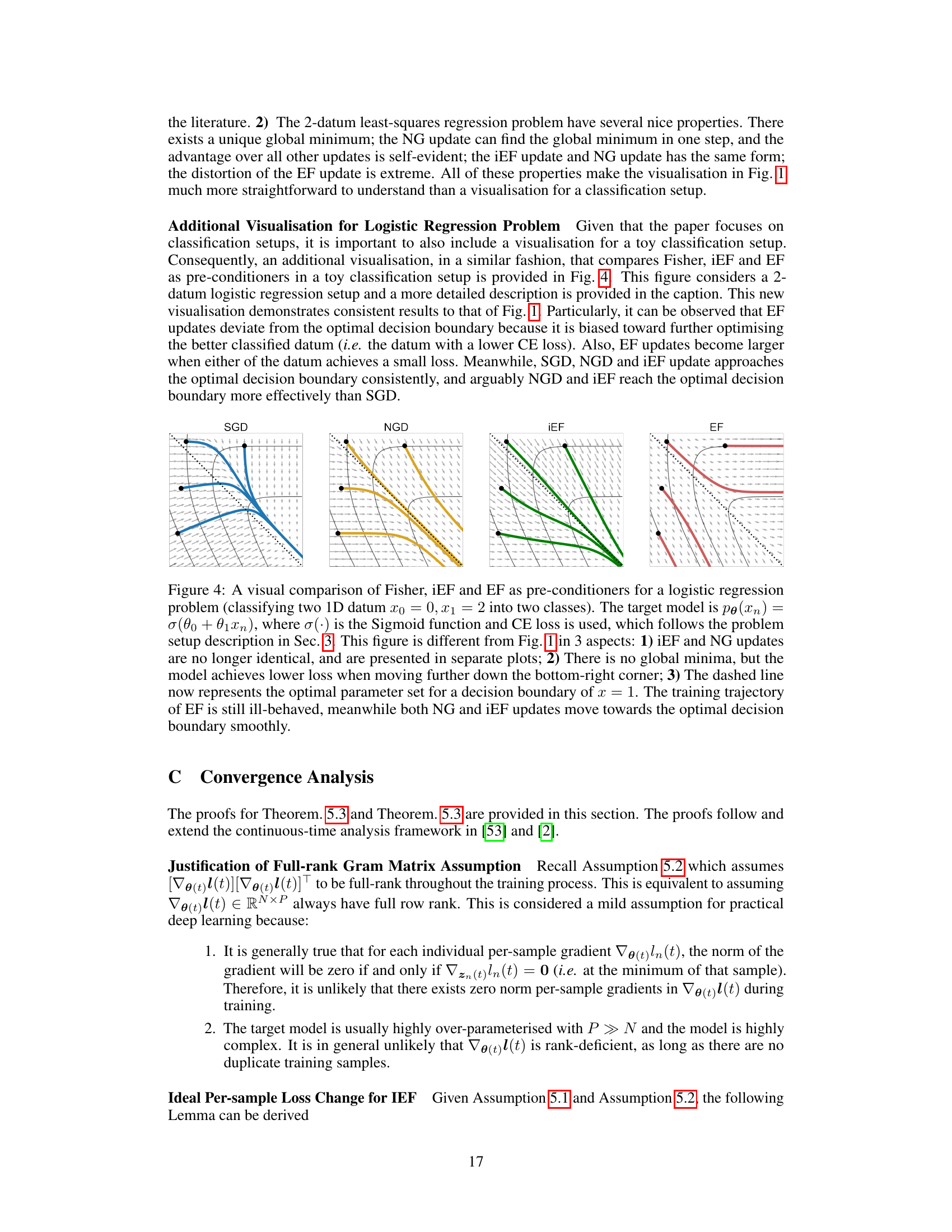
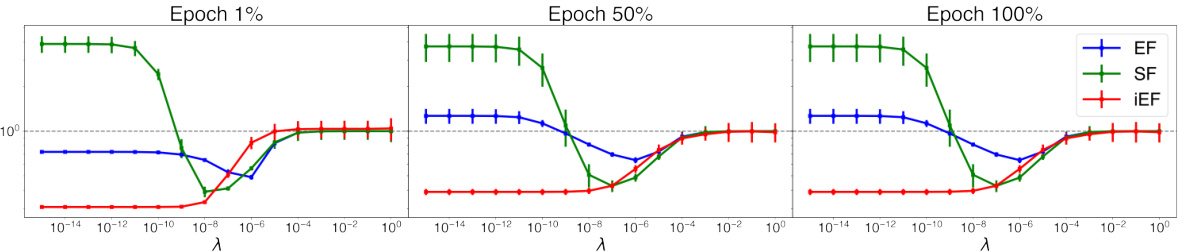
This figure compares the approximation quality of EF, SF, and iEF methods to the exact natural gradient update with respect to the damping factor (λ) at different training stages. The results show that iEF consistently provides better approximations than EF and SF, especially with near-zero damping factors. EF and SF are highly sensitive to the choice of damping factor, requiring careful tuning across tasks and training stages.
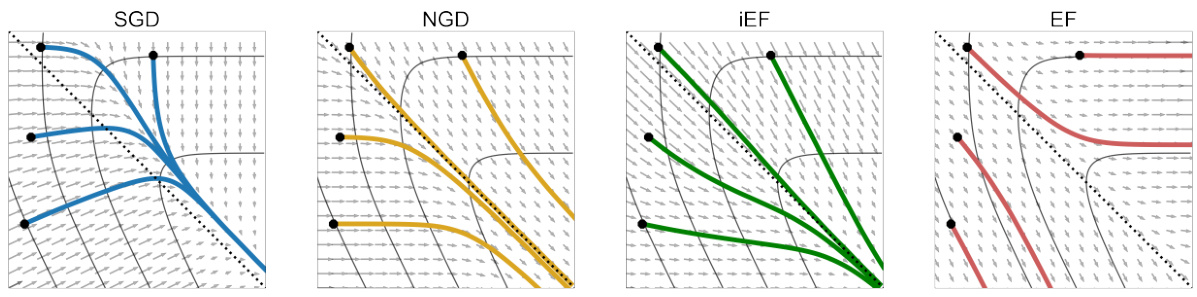
This figure compares the update vector fields and training trajectories of four optimization methods (SGD, NGD, iEF, and EF) on a simple 2D linear least squares regression problem. It visually demonstrates the inversely-scaled projection issue of the EF method, showing how its update vector field is distorted and biased towards well-trained samples, leading to inefficient training. In contrast, NGD and iEF demonstrate more efficient and accurate convergence to the global minimum.
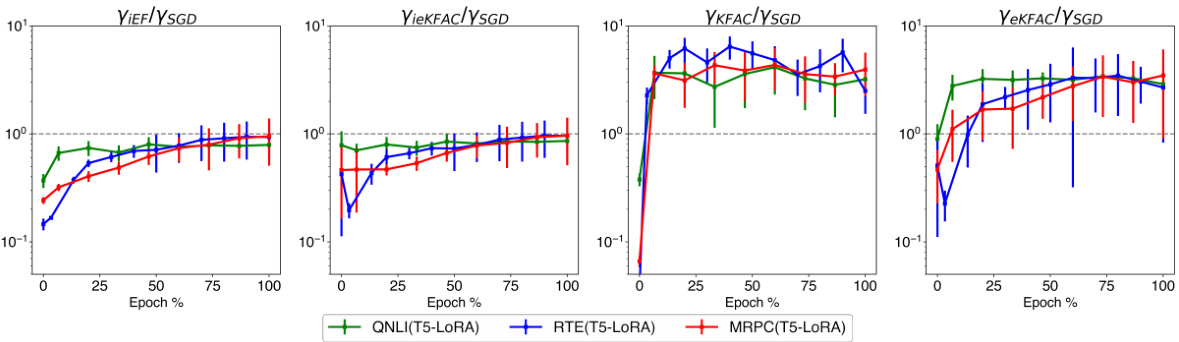
This figure compares the approximation quality of four methods: iEF, ieKFAC, KFAC, and eKFAC to the exact natural gradient descent update. The results are shown for three different tasks across various training stages. The y-axis shows the ratio of each method’s approximation quality to that of SGD, lower values indicating better approximations. The plot shows that ieKFAC consistently performs better than KFAC and eKFAC and approximates iEF well.
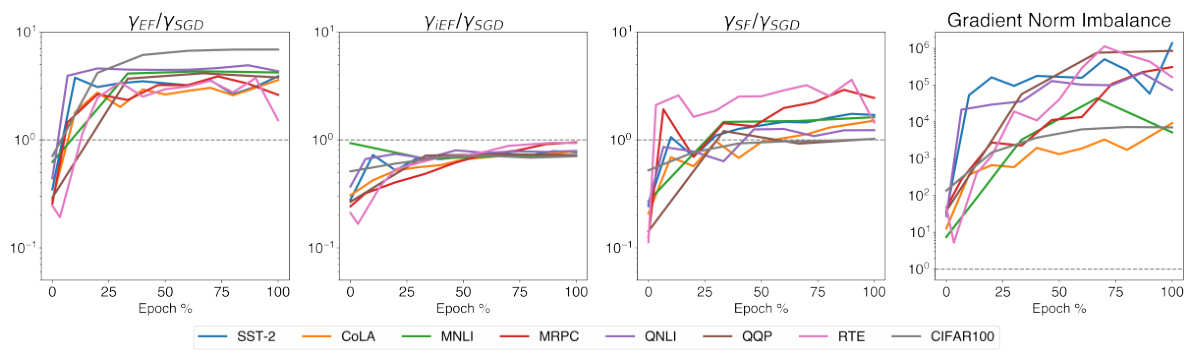
This figure compares the approximation quality of EF, iEF, and SF methods to exact NG updates across different training stages. Four plots are shown, visualizing: 1) EF’s relative improvement over SGD; 2) iEF’s relative improvement over SGD; 3) SF’s relative improvement over iEF; and 4) the imbalance of gradient norms across samples. The results indicate that iEF consistently provides better approximation quality than EF and SF.
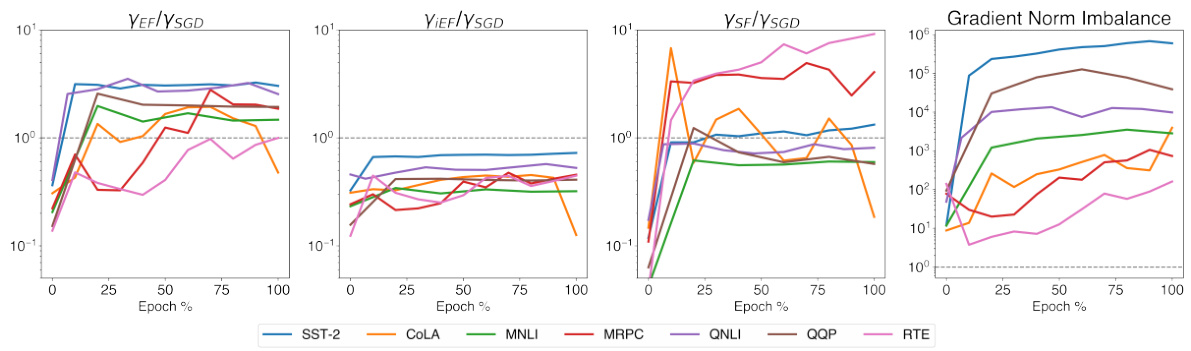
This figure presents a comparison of the approximation quality of three different methods (EF, iEF, and SF) to the exact natural gradient update against SGD. The plots show the ratio of the approximation quality of each method relative to SGD across different training stages, for three example tasks. The final plot displays the gradient norm imbalance across these tasks, which correlates with the approximation quality of the methods. The results indicate that iEF generally provides the best approximation.
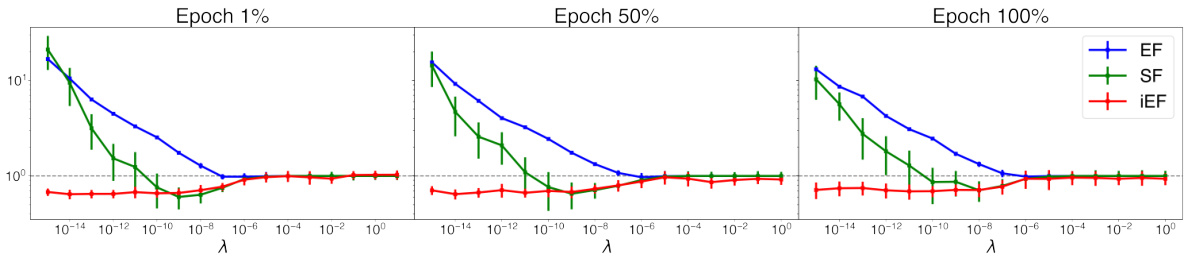
This figure shows how the approximation quality of EF, SF, and iEF methods changes with different damping factors (λ) at various training stages for the CoLA+T5+LoRA task. The results demonstrate that iEF consistently outperforms EF and SF, especially with near-zero damping factors. This highlights iEF’s robustness and superior approximation quality compared to other methods.
This figure compares the update vector fields of three different methods (Fisher, iEF, and EF) in a simple 2-parameter, 2-datum linear least-squares regression problem. The plots show the loss landscapes and training trajectories for SGD, NGD/iEF, and EF updates. The EF method’s update vector field is highly distorted compared to the NGD/iEF method, which adapts effectively to the problem’s curvature.
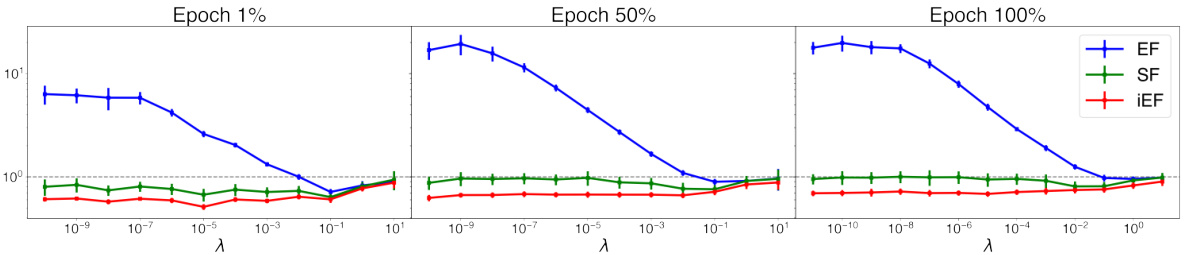
This figure compares the approximation quality of EF, SF, and iEF methods to the exact natural gradient update at different training stages for the CoLA+T5+LoRA task. It shows how the approximation quality changes with the damping factor (λ), demonstrating that iEF consistently performs well with near-zero damping, unlike EF and SF, which require careful tuning of λ across different training stages.

This figure compares the update vector fields and training trajectories of SGD, NGD/iEF, and EF methods on a simple 2D linear least squares regression problem. It shows how EF updates are biased towards well-trained samples due to inverse scaling, resulting in a distorted update vector field and inefficient training. In contrast, NGD/iEF updates adapt to the curvature of the problem, leading to more efficient training.
This figure compares the update vector fields and training trajectories of three different optimization methods (SGD, NGD/iEF, and EF) on a simple 2D linear least squares regression problem. The plots visualize the loss landscape, illustrating how each method’s updates behave differently in response to the problem’s curvature and the location of individual data points. The EF method shows a highly distorted update vector field and inefficient training trajectories, highlighting its limitations, while the NGD/iEF methods adapt well to the curvature, demonstrating their superiority.

This figure compares three different preconditioners (Fisher, iEF, and EF) for a simple linear least-squares regression problem. The plots show the loss landscape and training trajectories under SGD, NGD/iEF, and EF updates. It visualizes how the EF method suffers from an inversely-scaled projection issue, resulting in a distorted update vector field and inefficient training, while NGD/iEF updates efficiently adapt to the curvature of the problem.
This figure compares the update vector fields of three different methods: SGD, NGD/iEF, and EF, on a simple 2-parameter, 2-data point linear least-squares regression problem. The figure visually demonstrates the inversely-scaled projection issue in the EF method, showing how the EF updates are biased towards well-trained samples, leading to distorted trajectories and inefficient convergence. In contrast, SGD and NGD/iEF show efficient convergence to the global minimum.
This figure compares the approximation quality of EF, SF, and iEF methods to the exact natural gradient update at different training stages for the CoLA+T5+LoRA task. The x-axis represents the damping factor (λ), and the y-axis represents the relative approximation quality improvement over SGD (lower is better). The figure shows that iEF consistently outperforms EF and SF, especially with near-zero damping, highlighting its robustness and superior approximation quality.
More on tables

This table presents the average test performance results for different optimizers across multiple tasks (GLUE and CIFAR100). It shows the average test scores achieved by AdamW, Adafactor, SGD, EF, SF, and iEF optimizers. For GLUE tasks, the average across the seven individual tasks is reported. For tasks with two metrics, those metrics are averaged. The results highlight the best performing optimizer for each task, indicating the superior performance of the iEF optimizer compared to the others.

This table presents the average test performance of different optimizers (AdamW, Adafactor, SGD, EF, SF, and iEF) on GLUE and CIFAR100 datasets. For GLUE, the average across seven tasks is reported, with averages calculated for tasks having two metrics. The best validation accuracy checkpoint determines the reported test results. For comprehensive details, refer to Table 7.
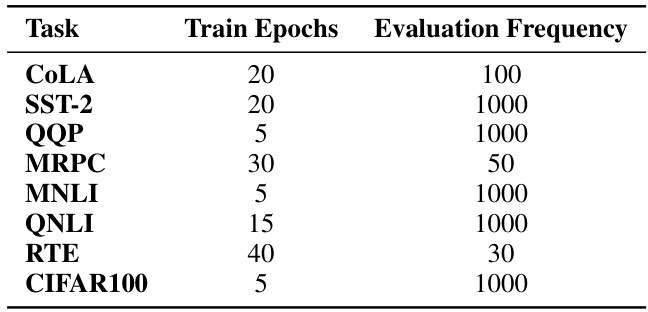
This table details the hyperparameters used for training different models on various tasks. It specifies the number of epochs used for training and the frequency at which the model’s performance was evaluated on a validation set during the training process.
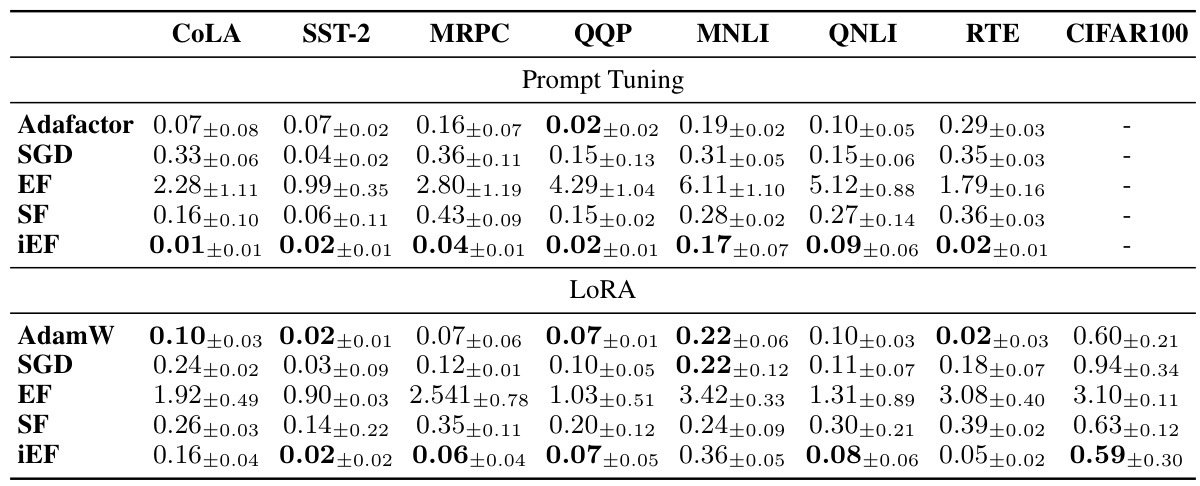
This table shows the test performance of different optimizers (AdamW, Adafactor, SGD, EF, SF, and iEF) on various tasks and model architectures (Prompt Tuning and LoRA). It displays the best test accuracy achieved for each combination and uses task-specific metrics (accuracy, F1-score, Matthew’s correlation coefficient). The table highlights the performance of each optimizer compared to others across different tasks.
This table presents the average test performance results for different optimization methods applied to GLUE and CIFAR100 datasets. It shows the average test scores for seven GLUE tasks and one CIFAR100 task, considering both Prompt Tuning and LoRA parameter-efficient fine-tuning methods. The table highlights the best-performing optimization method (iEF) across various tasks.
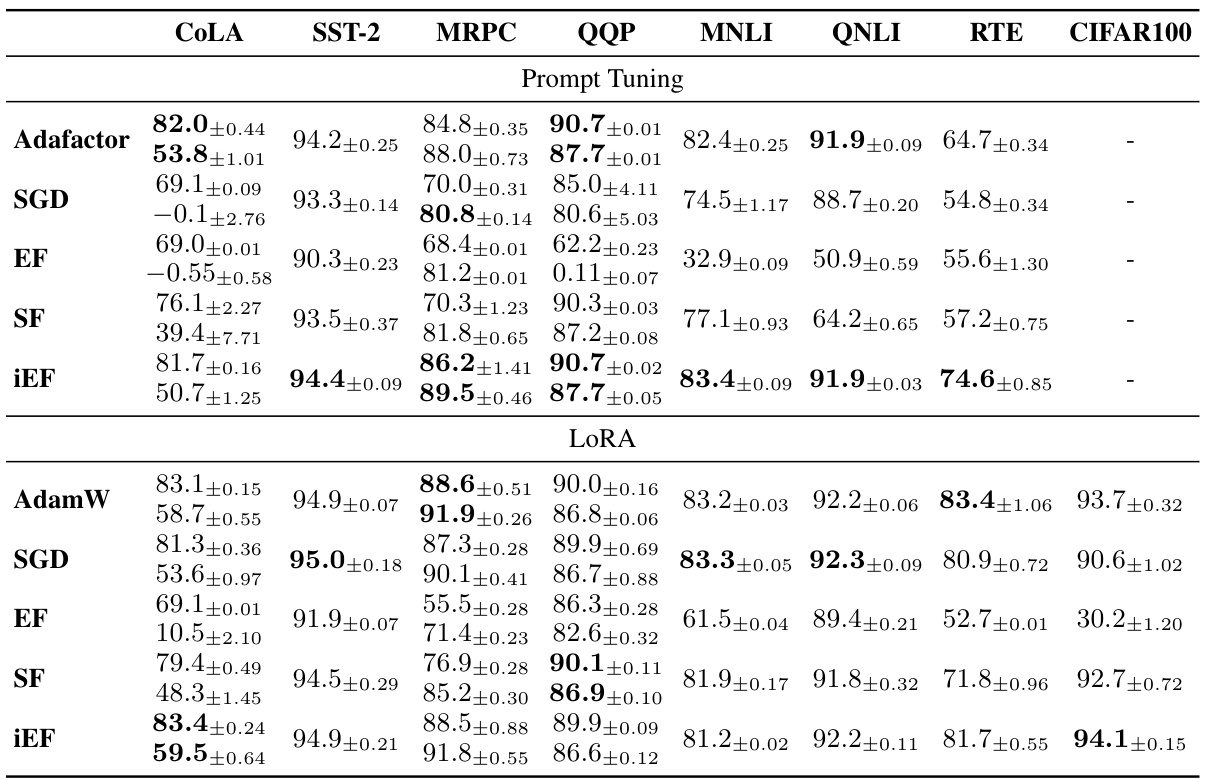
This table presents the average test performance results for different optimizers across various tasks (GLUE and CIFAR100). It shows the average test score for seven GLUE tasks and the CIFAR100 task. For GLUE, the average of the seven tasks’ metrics is reported, and for tasks with two metrics, those are averaged. The test results are based on the best validation accuracy checkpoint for each model. For more detailed results and metric explanations, refer to Table 7.
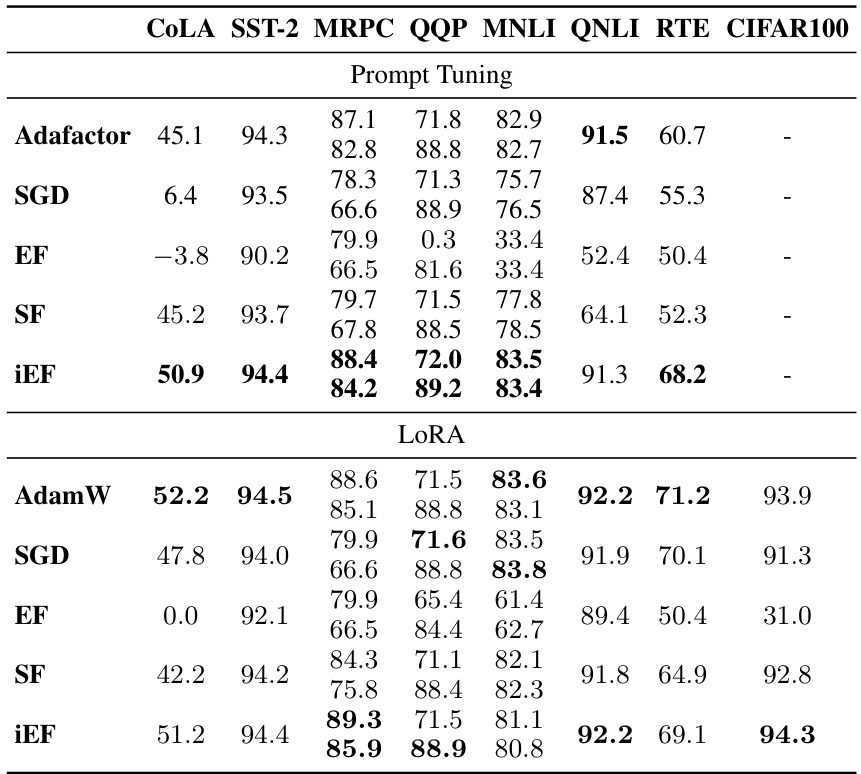
This table shows the average test performance of different optimization methods (AdamW, Adafactor, SGD, EF, SF, iEF) on the GLUE and CIFAR100 datasets. The average metric scores across the seven GLUE tasks are used as the final score; for tasks with multiple metrics, the averages are reported. The results represent the best validation accuracy checkpoint for each task and optimization method. For more detailed information, including individual task scores, consult Table 7.

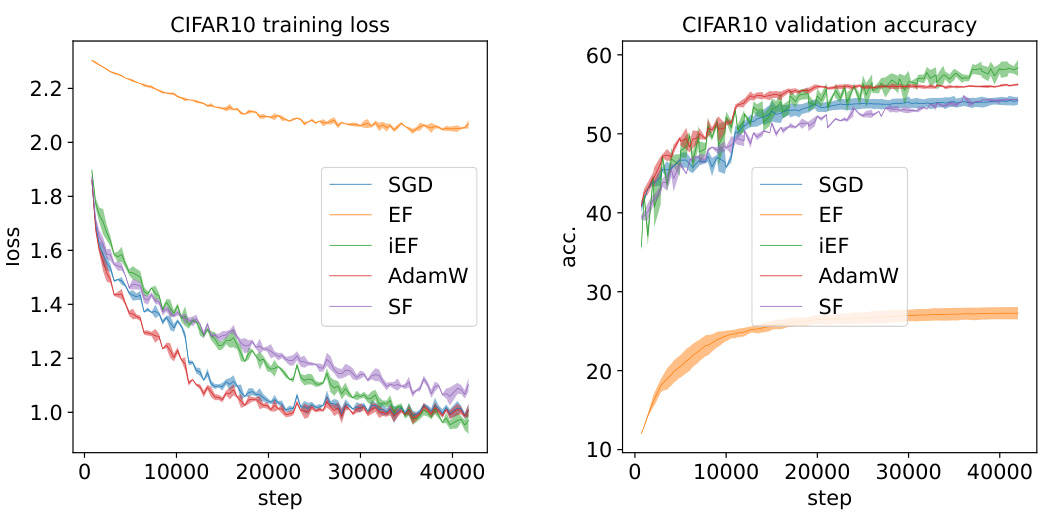
This table presents the validation and test accuracy achieved by different optimizers (iEF, Adam, SGD, SF, EF) when training a Multilayer Perceptron (MLP) model from scratch on the CIFAR-10 dataset. The results highlight the superior performance of the iEF optimizer in achieving higher accuracy compared to other methods.
Full paper#