↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning problems involve optimizing over multiple probability distributions, a task that’s often computationally expensive. Current methods often rely on strong assumptions like convexity, which limits their applicability and efficiency. This paper addresses these issues by introducing a new condition called “generalized quasar-convexity” (GQC), a less restrictive condition than convexity, for this type of problem.
The authors present novel adaptive algorithms based on this condition which are significantly faster than existing methods. They show that the iteration complexity of their algorithms does not explicitly depend on the number of distributions involved. Furthermore, they extend their work to minimax optimization problems (where we aim to find a saddle point) and successfully apply their methods to reinforcement learning problems and Markov games, showing significant improvements in algorithm convergence speed.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the challenge of optimizing problems involving multiple probability distributions, a common scenario in machine learning and other fields. It introduces novel theoretical conditions (GQC and GQCC) that go beyond traditional convexity, enabling faster optimization algorithms. The adaptive algorithms proposed offer improved iteration complexities compared to existing methods, making them more efficient for large-scale problems. These contributions are significant for advancing optimization techniques and have implications for various applications including reinforcement learning and Markov games.
Visual Insights#
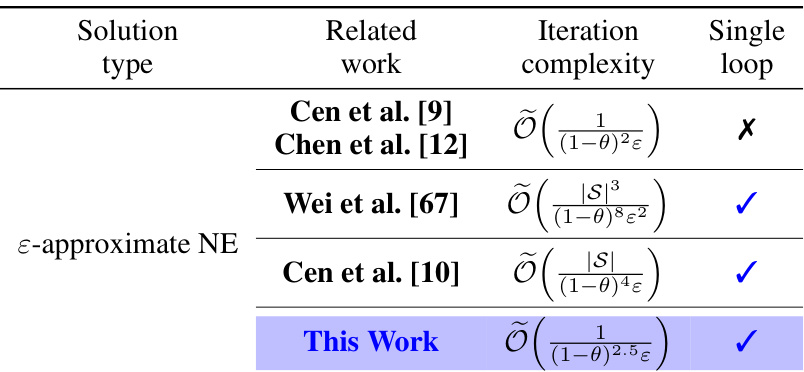
This table compares several policy optimization methods used to find an approximate Nash Equilibrium in infinite horizon two-player zero-sum Markov games. The comparison is based on the iteration complexity required to achieve a certain level of approximation (ε-approximate NE) of the solution. The table notes which methods use a single loop iteration process and highlights that the proposed method in this paper has a faster iteration complexity than those previously published.
Full paper#



















