MAC Advice for facility location mechanism design

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it challenges the standard approach to using predictions in mechanism design. By introducing a novel ‘Mostly Approximately Correct’ (MAC) prediction model that handles significant uncertainties, it opens new avenues for designing robust and efficient mechanisms in various domains, particularly facility location. Its findings on robustness may also be of independent interest to researchers in robust statistics.

Visual Insights

#

This figure illustrates an example where a single bad prediction in a 2-facility location problem on a line leads to an unbounded worst-case error and approximation ratio. The left side shows the predictions (X’), with one point incorrectly predicted at a very large distance M from the others. The right side shows the actual locations of the points (X). The optimal solution for the actual locations is shown with triangles, demonstrating a significant cost increase compared to the optimal solution for the predictions.

This table summarizes the approximation ratios achieved by deterministic mechanisms for facility location problems, comparing the best-known results without predictions to those obtained using Mostly Approximately Correct (MAC) predictions. It shows that using MAC predictions improves upon the no-prediction bounds for both single-facility location and balanced k-facility location in Rd.

In-depth insights

#

MAC Prediction Model

#

The MAC (Mostly Approximately Correct) prediction model is a novel approach to incorporating predictions into algorithmic design, particularly within mechanism design. It addresses the limitations of traditional prediction error models which are highly sensitive to outliers. Unlike models that assume perfect or near-perfect predictions, MAC acknowledges that a certain fraction of predictions might be arbitrarily inaccurate. This is crucial for real-world applications where perfect predictions are unrealistic. The MAC model introduces parameters (ε and δ) to quantify the level of uncertainty. Epsilon (ε) defines the maximum allowable error for the majority of the predictions, whereas delta (δ) represents the fraction of predictions allowed to be arbitrarily incorrect. This robustness to outliers is a key strength of the model, allowing for useful results even with noisy data. The model’s ability to work effectively despite prediction errors makes it particularly suitable for applications where machine learning predictions are used as advice. Furthermore, the MAC model considers both the trustworthiness and error bounds of predictions, a feature that sets it apart from previous models that focus solely on one aspect of prediction error.

Robustness of Estimators

#

The concept of robustness in estimators is crucial for reliable statistical analysis, especially when dealing with real-world data often containing errors or outliers. The paper likely explores how much the estimator’s output changes when a certain fraction of the input data is modified. A key aspect is the balance between robustness and efficiency: highly robust estimators might sacrifice accuracy. The study probably introduces quantitative measures of robustness to analyze the behavior of estimators (like the median and its generalizations) when facing data corruptions. The findings likely demonstrate that classic results on breakdown points can be made quantitative and help in designing mechanisms for facility location that are resilient to prediction errors. This quantitative approach is essential for practical applications. The analysis might highlight trade-offs between robustness to outliers and the estimator’s accuracy in the ideal case. The paper emphasizes the smoothness of the median’s robustness: indicating that even with a substantial fraction of errors, the outcome remains relatively stable, providing valuable insights for robust statistical inference and mechanism design. This is particularly relevant when handling datasets with noisy or uncertain inputs, as seen in machine learning applications or strategic settings.

Mechanism Design

#

The research paper explores mechanism design within the context of facility location problems, focusing on scenarios where algorithms leverage predictions about agent locations. A key contribution is the introduction of the Mostly Approximately Correct (MAC) prediction model, which acknowledges that predictions may contain a certain fraction of arbitrarily large errors. This contrasts with previous work that assumes perfect or near-perfect predictions. The paper designs both deterministic and randomized strategyproof mechanisms for facility location that utilize MAC predictions, achieving improved approximation ratios compared to existing mechanisms without predictions. A core idea is that the robustness of the geometric median allows for resilience against prediction errors, and the paper extends this to balanced facility location. The work introduces the problem of second facility location, further highlighting the relevance of incorporating prediction uncertainty in mechanism design. Overall, this study provides significant advances in mechanism design by incorporating the realistic limitations of prediction accuracy into the model.

2-Facility Location

#

The research paper delves into the 2-facility location problem, a significant challenge in mechanism design. Standard approaches often struggle with prediction errors, especially when a considerable fraction of predictions are inaccurate. The authors introduce a novel model, Mostly Approximately Correct (MAC), to address these limitations by allowing a certain percentage of predictions to be arbitrarily inaccurate. For the 2-facility problem on a line, they design a randomized truthful mechanism. This mechanism outperforms existing mechanisms (without predictions) by leveraging the robustness of the 1-median and introducing a clever ‘second facility location’ subroutine to handle the uncertainty in predictions. The robustness analysis highlights the smooth relationship between prediction accuracy and algorithmic performance, demonstrating the value of incorporating even imperfect predictions into mechanism design. A key takeaway is that the MAC model offers a new pathway for designing robust mechanisms, going beyond simply interpolating between the best case with perfect predictions and worst-case scenarios with no predictions.

Future Directions

#

The research paper’s “Future Directions” section would ideally explore several avenues. Addressing the open question of a deterministic mechanism for 2-facility location on a line with a constant approximation ratio is crucial. This would complement the current randomized mechanism and offer a more practical solution. Further research should focus on improving the approximation ratios achieved by both the deterministic and randomized mechanisms. Investigating the interplay between predictions and agent-reported values could lead to more efficient algorithms. This involves moving beyond the independent treatment of these two data sources. Finally, extending the MAC prediction model and the developed mechanisms to other facility location problems and beyond would showcase the model’s broader applicability. This could include considering different cost functions or exploring non-strategic online settings. The overall goal should be to enhance the robustness and efficiency of algorithms when incorporating imperfect predictions.

More visual insights

#

More on figures

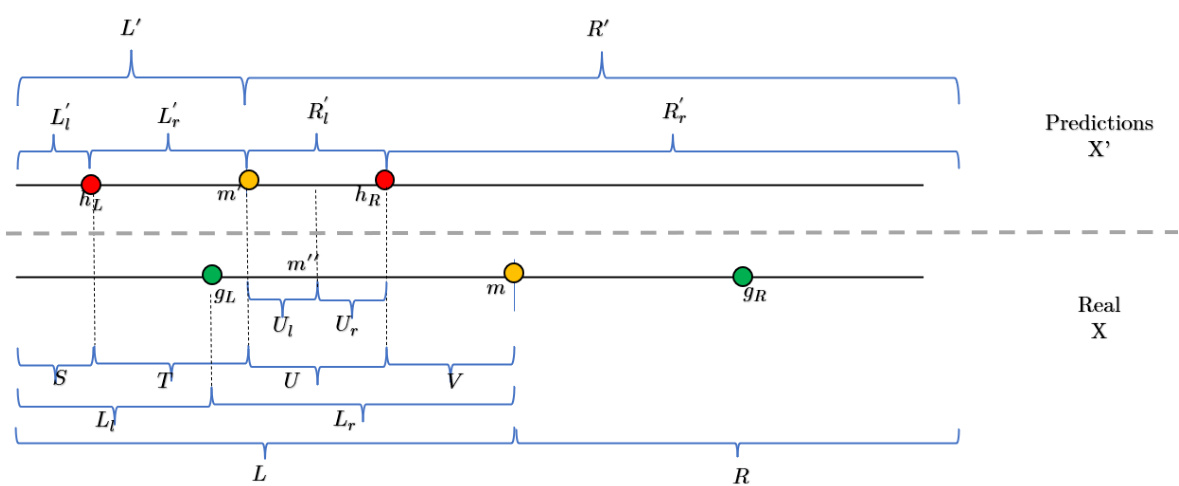
This figure illustrates case 4 of the proof of Theorem 8 in Section H.1.2 (8-robustness of the big cluster center) where m’ < gL. It shows the relationships between the ‘predicted’ and ‘real’ locations of points, highlighting how the algorithm handles differences in the two datasets. It helps to visualize the four disjoint multi-sets (S, T, U, V) and their partitions (L’₁, L’r, R’₁, R’r, L₁, Lr, R₁, Rr) within the datasets and their use in the approximation robustness calculations.

This figure illustrates the four cases used in the proof of Theorem 8 (case 4 specifically). It shows the relationship between the ‘predicted’ locations (X’) and the ‘real’ locations (X) for the 2-facility location problem. The figure highlights how the algorithm’s estimated locations (hL, hR) relate to the optimal locations (gL, gR). The key partitions and sub-partitions of the datasets are also presented, which are important for understanding the proof’s arguments.

More on tables

This table summarizes the approximation ratios achieved by randomized mechanisms for the 2-facility location problem on a line, comparing the best-known result without predictions to the result obtained using Mostly Approximately Correct (MAC) predictions. The table highlights the improvement in approximation ratio gained by leveraging MAC predictions.

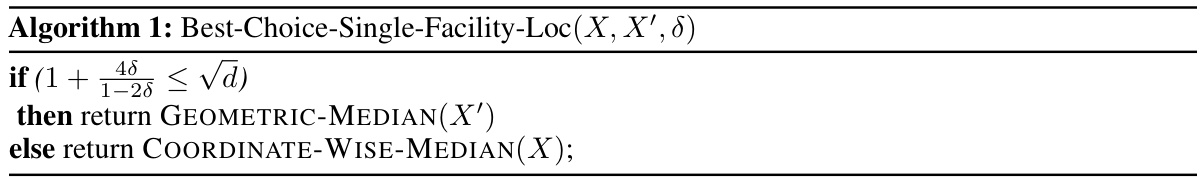
This table summarizes the approximation ratios achieved by deterministic mechanisms for single-facility location in R^d and β-balanced k-facility location in R^d, both with and without MAC predictions. It highlights the improvement obtained by leveraging MAC predictions in terms of approximation ratios, comparing the results to the best-known approximation ratios achievable without the use of predictions. For single-facility location, the table shows how the approximation ratio improves with sufficiently small δ. For β-balanced k-facility location, the constant approximation ratio obtained with MAC predictions represents a significant advancement over the previously unknown approximation ratio without predictions.

This table summarizes the approximation ratios achieved by deterministic mechanisms for single-facility location in Rd and β-balanced k-facility location in Rd, both with and without MAC predictions. It highlights the improvements gained by using MAC predictions in terms of approximation ratios. Note that the linear approximation ratio for β-balanced k-facilities is from Aziz et al. (2020) and refers to a capacitated facility location variant.

This table summarizes the results for deterministic mechanism design. It compares the best-known approximation ratios achievable without using predictions to the approximation ratios obtained using Mostly Approximately Correct (MAC) predictions for two facility location problems: single facility location in R^d and β-balanced k facilities in R^d. The table highlights the improvement in approximation ratios gained by leveraging MAC predictions.

This table summarizes the approximation ratios achieved by deterministic mechanisms for single facility location in Rd and β-balanced k facilities in Rd, both with and without MAC predictions. It compares the approximation ratios obtained using the proposed MAC prediction-based mechanisms to the best-known approximation ratios achievable by mechanisms that do not use predictions.

This table summarizes the approximation ratios achieved by deterministic mechanisms for single-facility location in R^d and β-balanced k-facility location in R^d, both with and without using Mostly Approximately Correct (MAC) predictions. The ‘Best known ’no predictions’ approximation ratio’ column shows the best approximation ratio achievable by any deterministic strategyproof mechanism in the absence of predictions. The ‘Approximation ratio obtained using MAC predictions’ column shows the approximation ratio obtained when incorporating MAC predictions into the mechanism design.

This table summarizes the approximation ratios achieved by deterministic mechanisms for single-facility location in Rd and β-balanced k-facility location in Rd, both with and without MAC predictions. It highlights the improvement obtained by using MAC predictions, showing how the robustness of the algorithms allows for better results than the best-known algorithms in the ’no predictions’ case.

This table summarizes the approximation ratios achieved by deterministic mechanisms for single-facility location in Rd and β-balanced k-facility location in Rd, both with and without MAC predictions. It highlights the improvement gained by leveraging MAC predictions in achieving better approximation ratios compared to the best-known results without predictions.

Full paper

#