↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning tasks require invariance to transformations like rotations or translations. The G-Bispectrum, a powerful tool for achieving this, has been computationally expensive, limiting its use. Traditional methods, like average pooling, are also highly lossy, discarding valuable information. This paper tackles the computational challenge.
The authors present a selective G-Bispectrum algorithm that significantly reduces computational complexity. They demonstrate the algorithm’s effectiveness across several group types commonly encountered in machine learning. Experimental results confirm that their approach provides comparable accuracy with considerable speed gains over traditional methods, making G-invariant deep learning more practical for large-scale applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in geometric deep learning and signal processing. It significantly reduces the computational cost of a foundational tool, the G-Bispectrum, for achieving G-invariance in neural networks. This breakthrough enables broader applications of G-invariant methods to more complex tasks and larger datasets, opening new avenues for research in fields like computer vision, time-series analysis, and more.
Visual Insights#

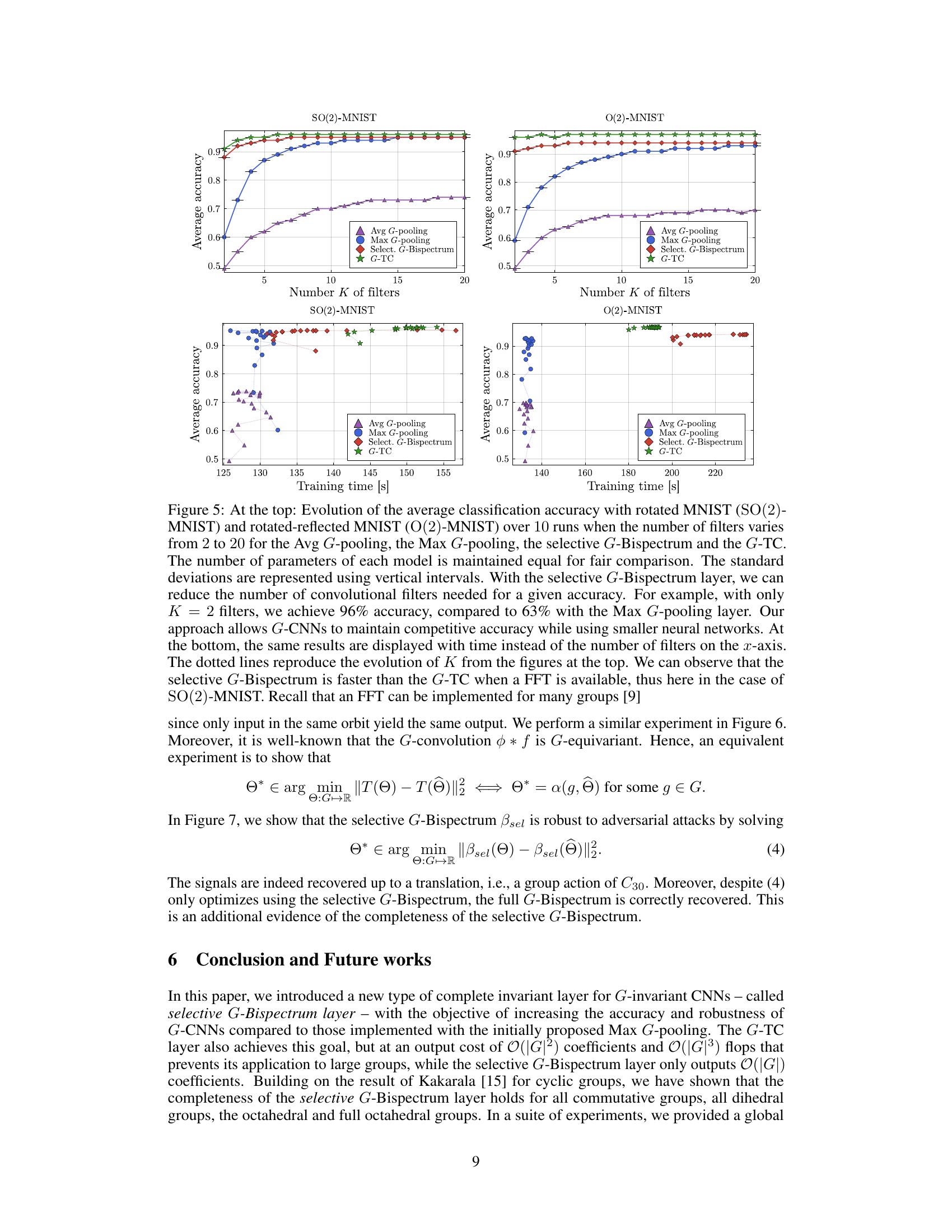
This figure compares the training time of different invariant layers (Avg G-pooling, Max G-pooling, Selective G-Bispectrum, and G-TC) in G-CNNs for SO(2) and O(2) MNIST datasets as the size of the discretization group (Cn/Dn) increases. It highlights the significant speed advantage of the Selective G-Bispectrum, especially when using FFT.
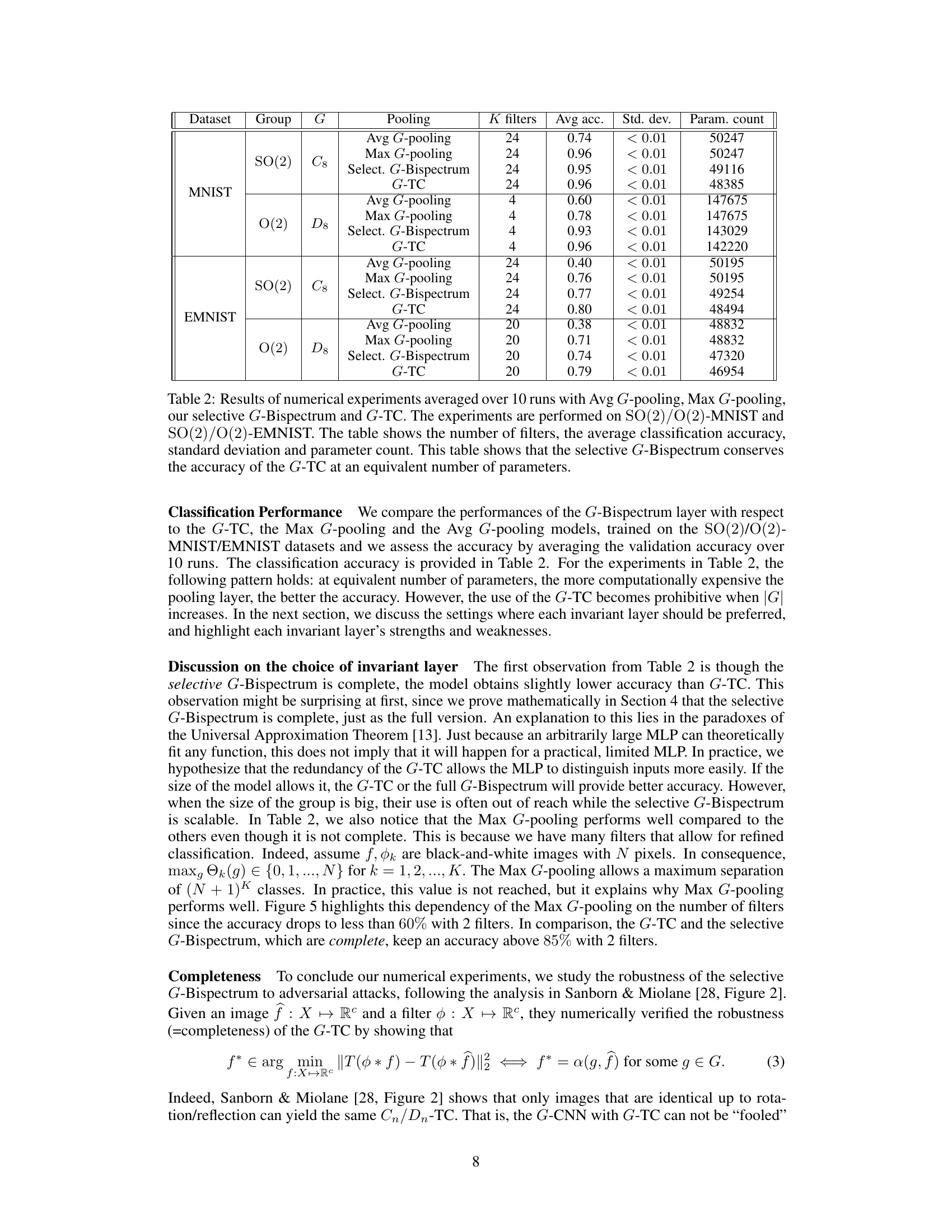
This table presents the results of experiments comparing four different G-invariant pooling methods (Avg G-pooling, Max G-pooling, selective G-Bispectrum, and G-TC) on the SO(2) and O(2) versions of the MNIST and EMNIST datasets. The comparison is done based on the number of filters used, the average classification accuracy achieved, the standard deviation of the accuracy, and the total number of parameters in each model. The key finding is that the selective G-Bispectrum achieves similar accuracy to the G-TC method, but with fewer parameters.
In-depth insights#
Selective Bispectrum#
The concept of a “Selective Bispectrum” presents a significant advance in signal processing, particularly within the context of G-invariant networks. By strategically reducing the computational complexity of the full bispectrum from O(|G|²) to O(|G|) or O(|G|log|G|) using an FFT, it offers a more efficient way to achieve G-invariance while preserving the crucial property of completeness. This enhanced efficiency is particularly beneficial for deep learning applications, where the computational cost of traditional G-invariant methods has often limited their use. The selectivity is achieved by intelligently selecting a subset of the bispectrum’s coefficients, exploiting redundancies inherent in the full calculation. The theoretical underpinnings, proven through mathematical theorems for important group structures (commutative groups, dihedral groups, octahedral groups), are as important as the practical gains in speed and reduced memory usage. Complete G-invariance, a key desirable property, is maintained by the selective bispectrum for these groups. Experimental results show significant speed improvements in training compared to the full bispectrum, opening the door for application to more complex symmetries and larger datasets. The balance between computational efficiency and the preservation of signal information makes the selective bispectrum a powerful tool for applications demanding G-invariance, offering a practical solution that overcomes the limitations of prior methods.
G-Invariant Networks#
G-invariant networks are a class of neural networks designed to be robust to transformations described by a group G. This is crucial because many real-world tasks involve data with inherent symmetries (e.g., image recognition should be invariant to rotations or translations). Traditional convolutional neural networks (CNNs) often achieve partial invariance through pooling layers, but these can be lossy, discarding important information. G-invariant networks aim to achieve complete invariance without such information loss, typically by leveraging group theory to construct layers that are inherently invariant to the group’s action. This often involves the use of techniques like group convolutions and higher-order spectral analysis (e.g., the G-Bispectrum). The main challenge is the high computational cost of achieving true invariance. This paper introduces a new, more efficient method using the selective G-Bispectrum, trading off some information for significant speedups, ultimately improving the robustness and efficiency of the network, particularly beneficial when dealing with datasets with large or complex group structures.
Computational Cost#
The research paper analyzes the computational cost of G-Bispectrum, a method used for achieving invariance in signal processing and deep learning. A significant challenge is the high computational cost of the full G-Bispectrum, scaling as O(|G|²), where |G| is the group size. This limits its applicability, especially for large groups. The paper’s core contribution is introducing the selective G-Bispectrum, which reduces the complexity to O(|G|) in space and O(|G|log|G|) in time if a Fast Fourier Transform (FFT) is available. This reduction is substantial, enabling its use in more complex scenarios. The paper further demonstrates the effectiveness of the selective G-Bispectrum through experimental results on MNIST and EMNIST datasets, showing enhanced accuracy and speed compared to existing approaches, particularly when the number of convolutional filters is low. Theoretical completeness of the selective G-Bispectrum for important group types is rigorously established, strengthening the claims of efficiency and accuracy gains.
Invariance Experiments#
Invariance experiments in the context of G-invariant networks are crucial for evaluating the effectiveness of proposed methods in achieving desired invariances while preserving relevant information. These experiments would typically involve applying various group transformations (e.g., rotations, translations) to input data and assessing how well the model’s output remains consistent despite these changes. Key aspects to consider include the choice of group transformations, the types of datasets used, and the metrics employed to quantify invariance. The experiments would need to demonstrate not only invariance to nuisance transformations but also the preservation of crucial information needed for the task at hand. A successful invariance experiment would show that the proposed method achieves higher accuracy or robustness compared to baselines such as simple averaging or max pooling while maintaining acceptable computational costs. Careful consideration of experimental design and analysis is necessary to draw meaningful conclusions regarding the efficacy of invariance methods.
Future Research#
Future research directions stemming from this work on the selective G-Bispectrum are manifold. Extending the theoretical completeness results to a broader range of group types beyond those proven (commutative, dihedral, octahedral) is crucial. This requires deeper investigation into the intricate algebraic structures of non-commutative groups and efficient methods for computing Clebsch-Gordan coefficients. Developing more sophisticated inversion algorithms that address phase ambiguities more robustly is also important. Current methods rely on assumptions of non-zero Fourier coefficients, a limitation that should be addressed. The integration of the selective G-Bispectrum into more complex G-CNN architectures is a key area for experimentation. Exploring its efficacy within different network designs and comparing it against other G-invariant pooling methods (e.g., average, max) in a broader set of tasks should provide further insights. Finally, investigating applications of the selective G-Bispectrum to different domains beyond image processing, such as in other areas of signal processing and deep learning involving group symmetries (e.g., graph neural networks, 3D shape analysis), is worthwhile. These directions represent promising avenues that build upon this work’s advancements, furthering the utility and theoretical understanding of G-invariant neural networks.
More visual insights#
More on figures
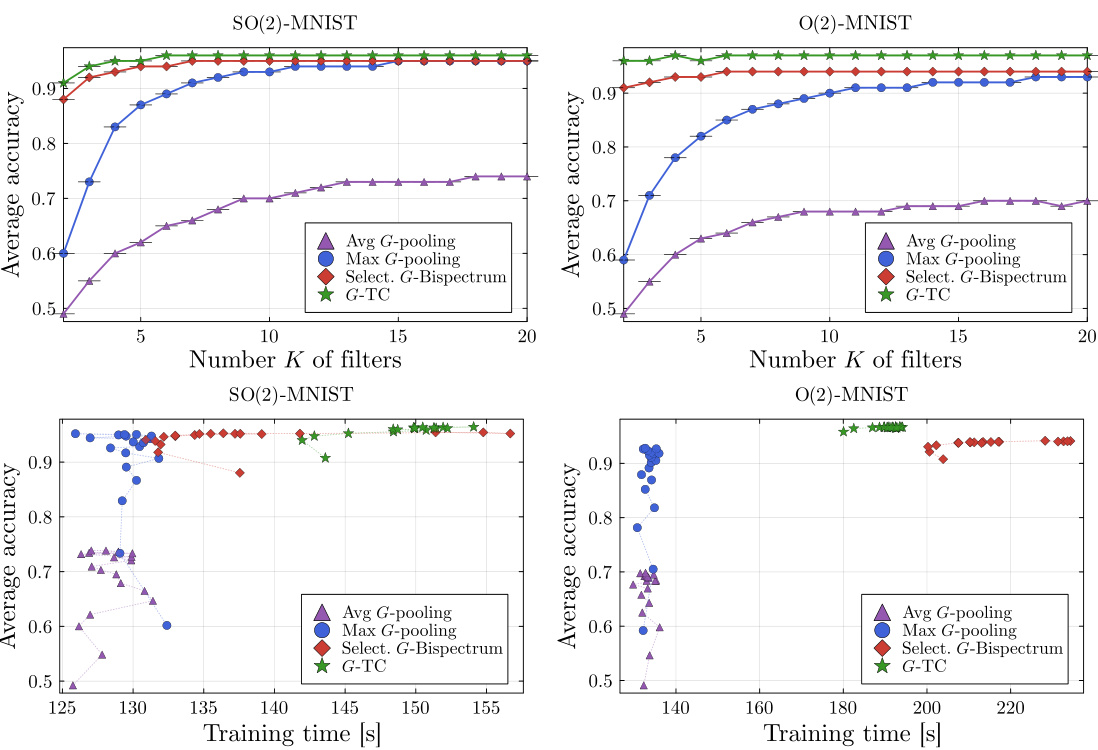
This figure compares the performance of four different G-invariant layers (Avg G-pooling, Max G-pooling, Selective G-Bispectrum, and G-TC) in a G-CNN on MNIST and EMNIST datasets. The top half shows the average classification accuracy as a function of the number of filters (K). The bottom half shows the same accuracy as a function of training time. The results demonstrate that the Selective G-Bispectrum achieves high accuracy with fewer filters and faster training times than the other methods, especially when a Fast Fourier Transform (FFT) is used.

This figure shows an experiment on adversarial attacks using the cyclic group C4. The goal is to compare the robustness of the selective G-Bispectrum and the Max G-pooling methods. The experiment optimizes images to produce a target output (either a specific selective G-Bispectrum or Max G-pooling value). The results show that the selective G-Bispectrum is robust, recovering an image identical to the original up to rotation. Conversely, the Max G-pooling method is not robust; it produces noisy images that are not in the same class as the originals. This demonstrates the complete nature of the selective G-Bispectrum and its resistance to adversarial attacks.
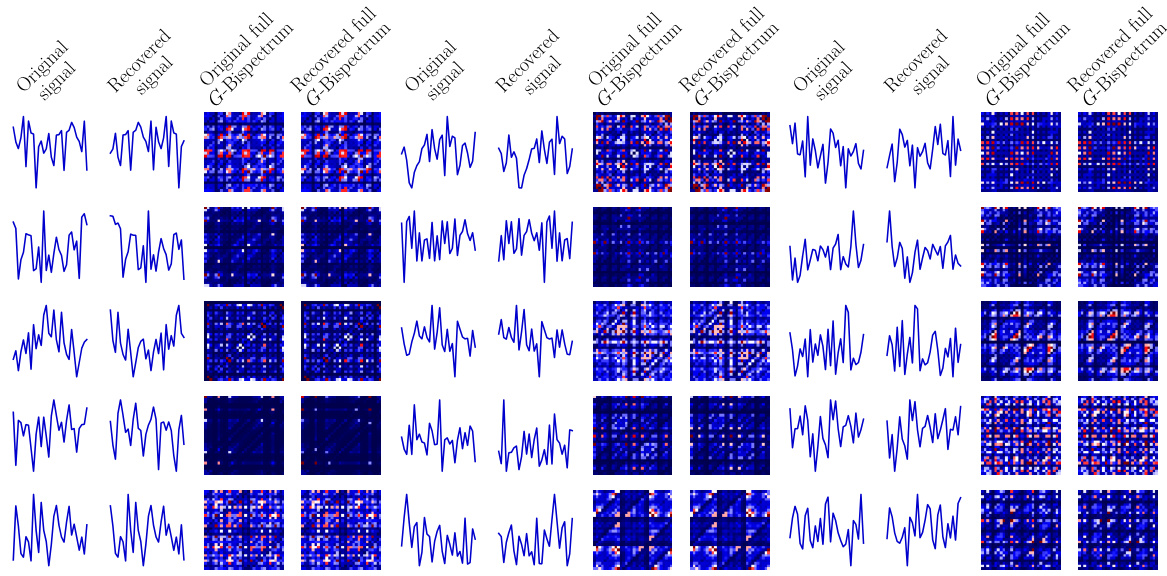
This figure shows numerical experiments of signal recovering from original signals using the selective G-Bispectrum with the cyclic group C30. The gradient method with Armijo line search is used to solve the optimization problem. The recovered signals are shown to be translations of the original signals, and their full G-Bispectra moduli are identical. This confirms the completeness of the selective G-Bispectrum, demonstrating that an unknown signal can be recovered using only its selective G-Bispectrum.

This figure illustrates the difference between excessive and complete invariance in the context of group actions. In the case of excessive invariance, different input samples (e.g., images of different objects) can be transformed by a group action (e.g., rotations) to yield the same output. This leads to a loss of information and reduces the effectiveness of the process. In contrast, complete invariance preserves all characteristics of an input sample up to the group action. This ensures that only inputs that are truly equivalent (i.e., differ only by the group action) will produce the same output. The figure uses a bispectrum to demonstrate how complete invariance avoids collapsing different classes into one.
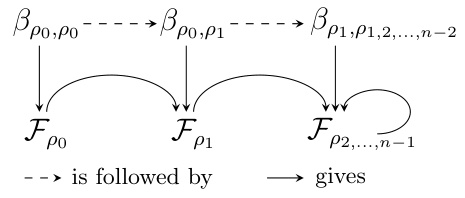
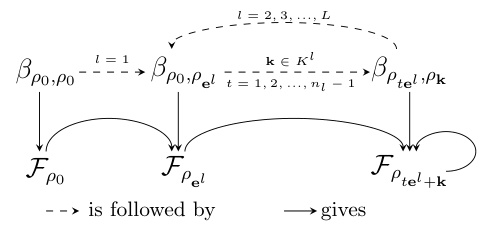
This figure is an illustration of the process described in Algorithm 2. It shows how the G-Bispectrum coefficients are used sequentially to recover the Fourier transform. The process starts with βρο,ρο which gives Fpo. Then βρ0,p1 is used with Fpo to obtain Fp1 and so on until all Fourier transforms are recovered.
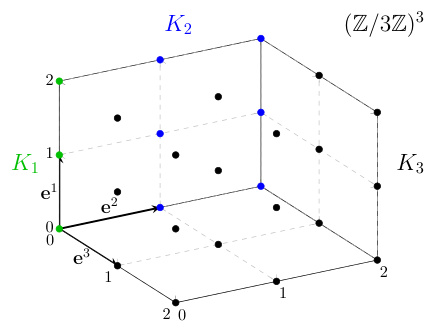
This figure visually represents the sets K1, K2, and K3 for the group G=(Z/3Z)3. These sets are recursively constructed in Algorithm 3 to generate the full group G from its generating set. Each set represents a stage in the iterative process of building up the group, starting with K1 and culminating in K3, which equals the entire group. The figure helps visualize how the algorithm systematically covers the entire group space by adding elements layer-by-layer.
This figure illustrates the architecture of a G-CNN, highlighting the different layers involved in achieving G-invariance. The input f undergoes a G-convolution with K filters, followed by a choice of invariant layer: Max G-pooling, G-Triple Correlation (G-TC), or selective/full G-Bispectrum. The output of the invariant layer is then fed into a neural network for classification.
More on tables

This table compares the performance of four different G-invariant pooling layers (Avg G-pooling, Max G-pooling, selective G-Bispectrum, and G-TC) on the SO(2) and O(2) versions of MNIST and EMNIST datasets. For each pooling method, it shows the average classification accuracy, standard deviation across 10 runs, the number of filters used, and the total number of parameters in the model. The results highlight that while the selective G-Bispectrum has comparable accuracy to the G-TC, it achieves this with significantly fewer parameters.
This table presents the results of a comparative study of four different G-invariant layers (Avg G-pooling, Max G-pooling, selective G-Bispectrum, and G-TC) in the context of SO(2) and O(2) group actions on MNIST and EMNIST datasets. The key metrics compared are average classification accuracy, standard deviation, the number of convolutional filters (K), and the total number of parameters in the model. The results highlight that the selective G-Bispectrum achieves comparable accuracy to the G-TC, while requiring a significantly smaller number of parameters.

This table compares the computational complexity and output size of different G-CNN invariant layers. It shows that the proposed selective G-Bispectrum achieves complete G-invariance with significantly lower computational cost and smaller output size compared to other methods like G-TC, while maintaining the desirable property of completeness.

This table presents the results of experiments comparing four different G-invariant pooling methods (Avg G-pooling, Max G-pooling, Selective G-Bispectrum, and G-TC) on the MNIST and EMNIST datasets. The results show average classification accuracy, standard deviation, and parameter counts for each method, using different numbers of filters (K). The key takeaway is that the selective G-Bispectrum achieves accuracy comparable to the G-TC with fewer parameters, indicating improved efficiency.

This table compares the computational complexity, output size, and completeness of different G-invariant layers used in G-CNNs. These layers are crucial for achieving invariance to nuisance factors in signal processing and deep learning. The table highlights the advantages of the proposed selective G-Bispectrum layer in terms of reduced computational cost and preserved information compared to the other methods.

This table summarizes the results of experiments comparing four different G-invariant pooling methods: Average G-pooling, Max G-pooling, the selective G-Bispectrum (proposed in this paper), and the G-Triple Correlation (G-TC). The experiments were run on MNIST and EMNIST datasets, modified to include rotations and reflections (SO(2) and O(2) groups). The table shows average classification accuracy, standard deviation, the number of filters used, and the total number of parameters for each method. Key observation is that the selective G-Bispectrum achieves accuracy comparable to G-TC with fewer parameters.

This table compares the computational complexity and output size of different G-CNN invariant layers: G-TC, full G-Bispectrum, selective G-Bispectrum, Max G-pooling, and Avg G-pooling. It highlights that the proposed selective G-Bispectrum achieves complete G-invariance with significantly lower computational cost and output size compared to the other methods.

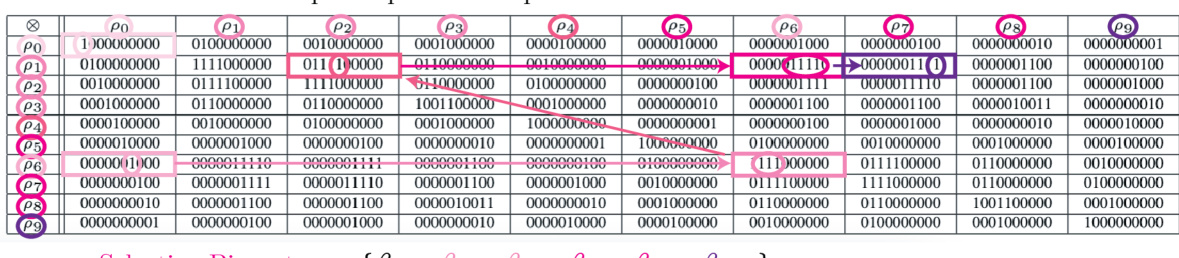
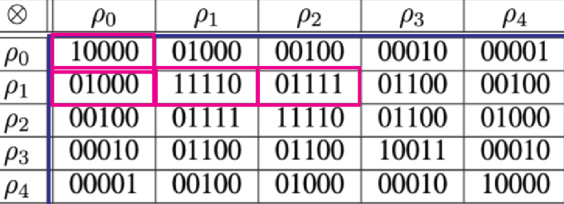
This table shows the Kronecker product of the irreps of the octahedral group. Each row and column represents an irrep (ρ₀, ρ₁, ρ₂, ρ₃, ρ₄). The entries are binary strings indicating which irreps result from the tensor product of the corresponding row and column irreps. A ‘1’ at position (i,j,k) means irrep ρₖ is present in the tensor product ρᵢ⊗ρⱼ, while ‘0’ means it is absent.

This table presents the results of a comparative study on different G-invariant layers used in G-CNNs. The study evaluates the average classification accuracy, standard deviation, and parameter count for four methods: Average G-pooling, Max G-pooling, the selective G-Bispectrum (the proposed method), and the G-Triple Correlation (G-TC). The experiment is performed on two datasets (SO(2)/O(2)-MNIST and SO(2)/O(2)-EMNIST) and for different group sizes. The results show that the selective G-Bispectrum achieves comparable accuracy to the G-TC but with significantly fewer parameters.
Full paper#