Probabilistic Graph Rewiring via Virtual Nodes

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it introduces IPR-MPNNs, a novel and efficient approach to address limitations in traditional graph neural networks. By implicitly rewiring graphs via virtual nodes, IPR-MPNNs overcome the scalability issues of graph transformers while significantly improving performance. This opens new avenues for research in large-scale graph learning, impacting various fields utilizing graph-structured data.

Visual Insights

#

This figure illustrates the architecture of Implicit Probabilistically Rewired Message-Passing Neural Networks (IPR-MPNNs). It shows how IPR-MPNNs implicitly rewire a graph by adding virtual nodes and learning to connect them to existing nodes via edges. An upstream MPNN learns prior probabilities for these connections, and exactly-k edges are sampled from this distribution. The resulting graph is then fed into a downstream MPNN for prediction. The figure also highlights the backward pass, showing how gradients are approximated using the derivative of exactly-k marginals.

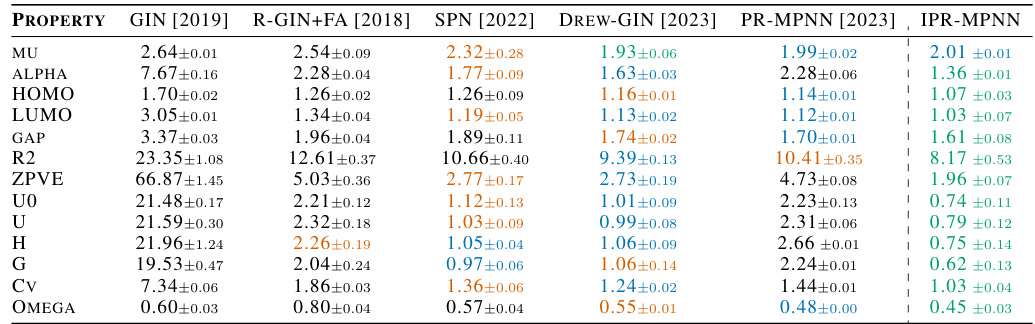
This table compares the performance of IPR-MPNN against several other state-of-the-art models on the QM9 dataset for predicting various molecular properties. The results highlight IPR-MPNN’s superior performance, achieving the best or second-best results across all properties.

In-depth insights

#

Virtual Node Rewiring

#

The concept of ‘Virtual Node Rewiring’ presents a novel approach to enhancing message passing in graph neural networks (GNNs). By introducing virtual nodes and probabilistically connecting them to existing nodes, this method implicitly rewires the graph, improving information flow and addressing limitations of traditional GNNs like under-reaching and over-squashing. This probabilistic rewiring is crucial because it allows the model to learn adaptive connections, focusing on long-range dependencies essential for many applications. Unlike explicit rewiring methods, which suffer from quadratic complexity, virtual node rewiring offers enhanced scalability due to its implicit nature. The use of differentiable sampling techniques makes the process end-to-end trainable, streamlining the learning process and optimizing the overall performance. This approach not only boosts the expressive power of GNNs but also leads to significant computational efficiency gains, outperforming more complex architectures like graph transformers.

IPR-MPNN: Method

#

The IPR-MPNN method section would detail the architecture and workflow of the Implicit Probabilistically Rewired Message-Passing Neural Network. It would likely begin by describing the upstream MPNN, which learns priors for connecting original nodes to virtual nodes. This process would involve using node features and the original graph’s adjacency matrix as input to the MPNN. The output of this MPNN would be a set of unnormalized prior probabilities. The section would then explain the differentiable k-subset sampling procedure, where exactly k edges are sampled from this probability distribution for each original node. This process is essential to connecting each original node to k virtual nodes, thereby implicitly rewiring the graph in a differentiable manner. The resulting graph with virtual nodes and added edges would be input into a downstream model (typically another MPNN) which would perform the final prediction task. The method section would also explain the backward pass and gradient estimation techniques used to optimize both the upstream and downstream MPNNs, likely focusing on how the gradients are backpropagated through the sampling process. Finally, the section would likely cover the computational complexity of the IPR-MPNN algorithm and how the use of virtual nodes contributes to a significantly improved efficiency compared to traditional graph transformers.

Expressiveness Gains

#

The concept of “Expressiveness Gains” in the context of graph neural networks (GNNs) refers to the enhanced ability of a model to capture complex relationships and patterns within graph-structured data. Standard message-passing GNNs are limited by their inherent locality, often failing to capture long-range dependencies. This limitation is addressed by techniques like the one proposed in the research paper, which enhances expressiveness by implicitly rewiring the graph through the introduction of virtual nodes. These virtual nodes act as intermediaries, facilitating information flow across greater distances in the original graph, thereby increasing the model’s receptive field. This improvement leads to better performance on tasks where long-range interactions are crucial. Theoretical analysis can demonstrate this expressiveness boost by showing that the modified architecture surpasses the capabilities of traditional MPNNs. Ultimately, expressiveness gains translate to better predictive accuracy and a broader range of applicability for GNNs, especially in complex domains such as molecular modeling.

Computational Speed

#

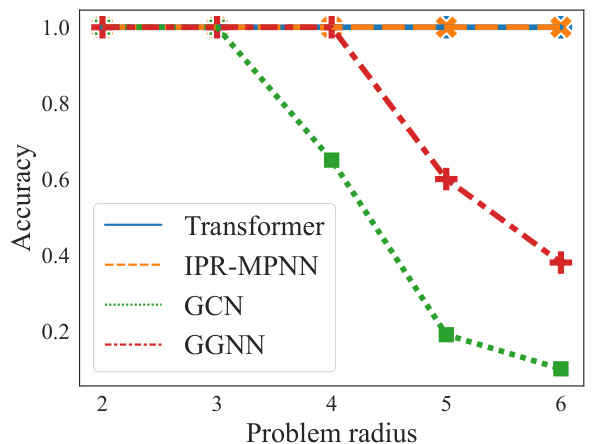
The computational speed of the proposed IPR-MPNN architecture is a crucial aspect of the research. The authors highlight that unlike traditional graph transformers and some graph rewiring methods which suffer from quadratic complexity, IPR-MPNNs achieve sub-quadratic time complexity. This is a significant advantage, as it enables the model to scale to much larger graphs. The improvement in computational efficiency is attributed to the implicit nature of the graph rewiring through virtual nodes, avoiding the need to compute scores for all possible node pairs. Empirical results demonstrate that IPR-MPNNs achieve state-of-the-art performance across multiple datasets while maintaining significantly faster computational efficiency compared to graph transformers. This speed advantage is further substantiated by the presented runtime statistics, showing IPR-MPNNs to be considerably faster than competing methods, underscoring the model’s practical benefits and scalability for large-scale graph applications. The linear scaling behavior is a key takeaway of the paper, promising significant computational gains over existing methods.

Future Work: Scope

#

A future work section focusing on the scope of probabilistic graph rewiring via virtual nodes could explore several promising avenues. Extending the approach to handle dynamic graphs would significantly enhance its practical applicability. This involves developing mechanisms to seamlessly integrate new nodes and edges while preserving the efficiency of the implicit rewiring scheme. Investigating the impact of different virtual node architectures, such as using varying numbers of virtual nodes or employing hierarchical structures, is crucial to optimize performance and expressivity. Theoretical analysis to refine the bounds on the model’s expressiveness is needed, going beyond the current comparison to the 1-dimensional Weisfeiler-Lehman algorithm. Furthermore, developing more robust gradient estimation techniques could improve training stability and scalability, especially for very large graphs. Finally, application to a wider range of graph datasets and tasks is vital to validate the generalized applicability and benefits of this approach.

More visual insights

#

More on figures

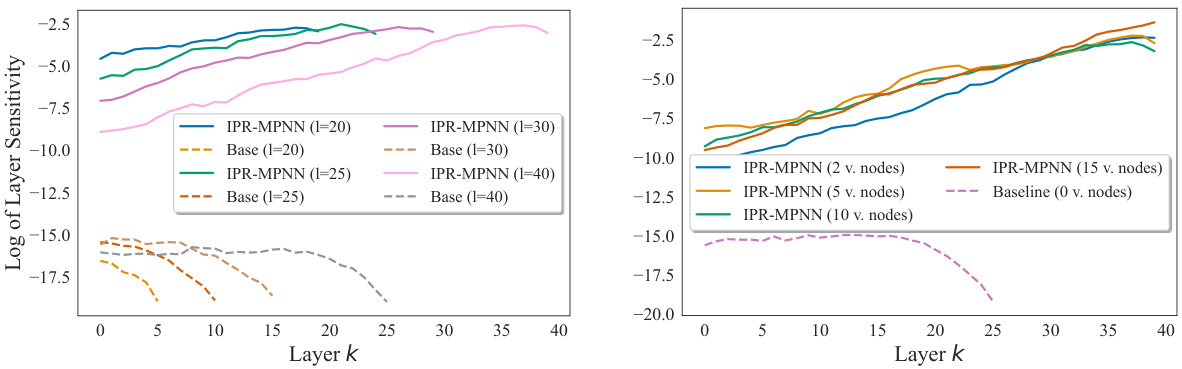
This figure compares the sensitivity of IPR-MPNN and baseline models across different layers for the two most distant nodes in graphs from the ZINC dataset. The left panel shows that IPR-MPNN maintains high sensitivity even in the last layer, unlike baseline models which decay to zero. The right panel demonstrates similar results for IPR-MPNN models with varying numbers of virtual nodes.

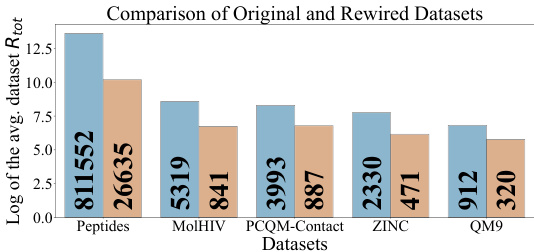
The figure shows a bar chart comparing the average total effective resistance (a measure of connectivity) before and after applying the proposed Implicit Probabilistically Rewired Message-Passing Neural Networks (IPR-MPNNs) method. Five molecular datasets (Peptides, MolHIV, PCQM-Contact, ZINC, QM9) are shown. For all datasets, the average total effective resistance is lower after applying IPR-MPNNs, indicating that the method effectively improves the flow of information within the graphs.

The figure compares the model sensitivity across different layers for two distant nodes in graphs from the ZINC dataset. The left panel compares sensitivity for models with varying numbers of layers, showing IPR-MPNNs maintain high sensitivity even in the last layer unlike base models. The right panel compares models with different numbers of virtual nodes, showing similar results across all variants.

The figure illustrates the process of implicit graph rewiring in IPR-MPNNs using virtual nodes. An upstream MPNN learns priors for connecting original nodes to virtual nodes, sampling k edges per original node. The resulting graph is then fed into a downstream MPNN for predictions, involving message passing between original and virtual nodes. The backward pass uses the derivative of exactly-k marginals to approximate gradients.

The figure illustrates the implicit graph rewiring mechanism of IPR-MPNNs. An upstream MPNN generates priors for connecting original nodes to new virtual nodes. Exactly k edges are sampled from this distribution, connecting each original node to k virtual nodes. A downstream MPNN then processes this augmented graph, facilitating long-range message passing. The backward pass uses the derivative of exactly-k marginals to approximate gradients.

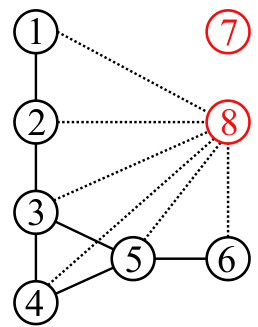
This figure illustrates the core idea of Implicit Probabilistically Rewired Message-Passing Neural Networks (IPR-MPNNs). It shows how IPR-MPNNs implicitly rewire a graph by adding a small number of virtual nodes and connecting them probabilistically to the existing nodes. An upstream MPNN learns the probability distribution for these connections, ensuring differentiability and efficient end-to-end training. The resulting modified graph is then fed into a downstream MPNN for prediction. The process involves message passing between original nodes and virtual nodes, and between virtual nodes themselves, thereby enabling long-range information flow and addressing limitations of traditional MPNNs.

More on tables

This table compares the performance of IPR-MPNNs against other state-of-the-art models on two datasets from the long-range graph benchmark: PEPTIDES and PCQM-CONTACT. The PCQM-CONTACT results are shown using three different evaluation methods, reflecting variations in data preprocessing. The best-performing model for each metric and dataset is highlighted.

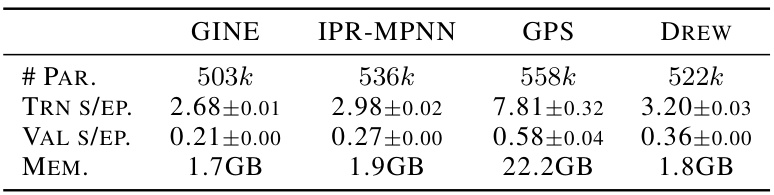
This table compares the training time, inference time, and memory usage of IPR-MPNN against three other models (GINE, GPS, and DREW) on the PEPTIDES-STRUCT dataset. The results show that IPR-MPNN achieves similar efficiency to GINE while significantly outperforming GPS in terms of speed and memory.

This table presents the results of the IPR-MPNN model and other state-of-the-art models on two molecular datasets: ZINC and OGB-MOLHIV. The results show the performance of each model on specific tasks (indicated by the ↑ or ↓ symbols), highlighting the superior performance of the IPR-MPNN model compared to other methods.

This table lists the hyperparameters used in the experiments for different datasets. It shows the number of hidden units in upstream and downstream MPNN layers, the number of virtual nodes, and sampling strategies. The hyperparameter settings were optimized for each dataset individually.

This table compares the performance of IPR-MPNN against several other models on the QM9 dataset for various molecular properties. The best performing model for each property is highlighted. The results demonstrate IPR-MPNN’s superior performance across different properties compared to existing methods.

This table compares the performance of the base GINE model and the proposed IPR-MPNN model on four recently proposed heterophilic datasets: ROMAN-EMPIRE, TOLOKERS, MINESWEEPER, and AMAZON-RATINGS. Heterophilic datasets are those where nodes of different classes tend to be connected to each other more frequently than nodes of the same class. The table shows that the IPR-MPNN model significantly outperforms the base GINE model on all four datasets. This improvement demonstrates the effectiveness of IPR-MPNNs in handling heterophily, a common challenge for many graph neural network models.

This table presents the performance comparison of different model variations on several datasets. The models vary in the number of virtual nodes and the number of samples used. The results show the impact of these variations on model accuracy.

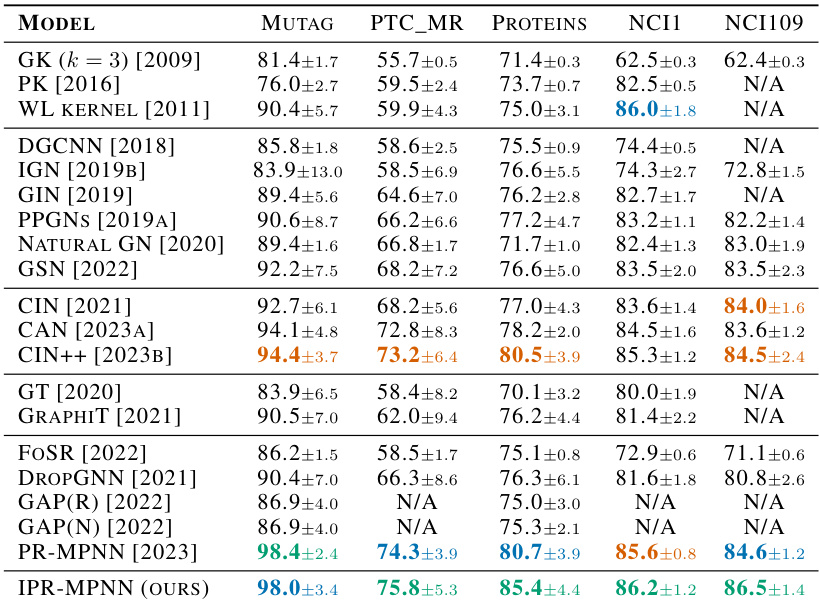
This table compares the performance of IPR-MPNN against several other state-of-the-art methods on the QM9 dataset for predicting various molecular properties. The results highlight IPR-MPNN’s superior performance across most properties.

This table compares the performance of IPR-MPNN against other state-of-the-art methods on the QM9 dataset for various molecular properties. The results show that IPR-MPNN significantly outperforms existing methods in most cases, demonstrating its effectiveness for molecular property prediction.

This table compares the performance of different models on the CSL dataset, focusing on the impact of positional encoding and the IPR-MPNN method. The base GIN model is compared against versions with positional encoding, the PR-MPNN method, and the IPR-MPNN method with and without pre-calculated graph partitioning (IPR-MPNN*). The accuracy for each model is presented, highlighting the performance improvements achieved by incorporating positional information and the IPR-MPNN technique.

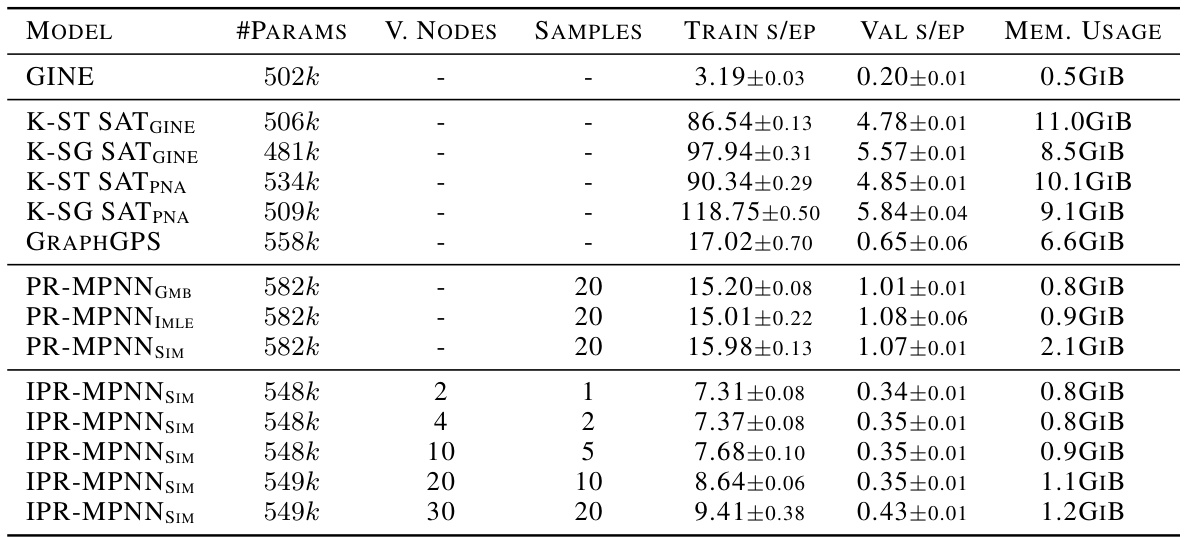
This table compares the training time, validation time, and memory usage of IPR-MPNN with other models on the OGB-MOLHIV dataset. It shows that IPR-MPNN achieves significantly faster training and validation times with lower memory consumption compared to graph transformers and the PR-MPNN method.

Full paper

#