Mind the Graph When Balancing Data for Fairness or Robustness

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because data balancing, a common technique in machine learning, is often used without considering its causal implications. The findings highlight the risk of unintended consequences and offer guidance for safer and more effective data balancing strategies. This directly impacts the fairness and robustness of AI models, making it highly relevant to current research trends in responsible AI.

Visual Insights

#

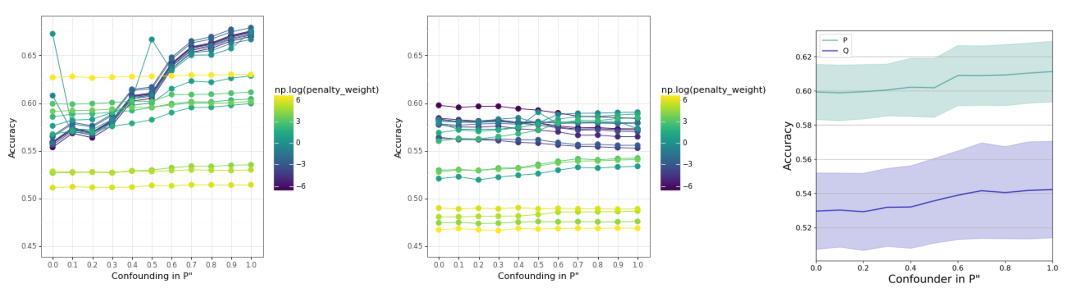
This figure displays the accuracy of models trained on balanced data for three different anti-causal tasks, each with varying levels of spurious correlation and confounding variables. The x-axis represents the strength of maximum mean discrepancy (MMD) regularization, and the y-axis shows accuracy. The left panel shows a purely spurious case, where data balancing succeeds even with regularization. The middle panel demonstrates a case where another confounder V negatively impacts the model’s performance after balancing. The right panel displays an entangled dataset where the model fails to generalize well. Red lines in each panel indicate worst group accuracy on the test distribution P⁰, emphasizing the importance of considering the impact of data balancing on the model’s fairness and robustness.

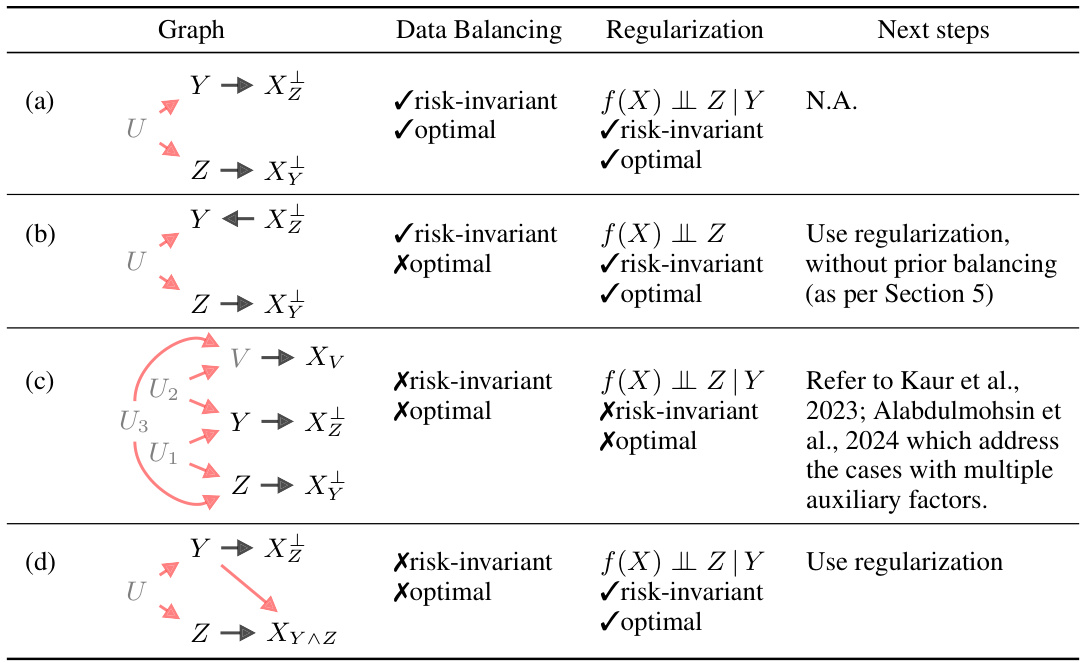
This table presents four causal Bayesian networks illustrating different scenarios of undesired dependencies between variables Y and Z. Each network shows whether data balancing leads to a risk-invariant and/or optimal model, comparing the results with regularization methods and proposing further steps to mitigate any remaining issues.

In-depth insights

#

Data Balancing Pitfalls

#

Data balancing, while seemingly a straightforward approach to improve fairness and robustness in machine learning models, harbors several pitfalls. Naively balancing datasets without considering the underlying causal relationships between variables can lead to unexpected and detrimental outcomes. This is because balancing may remove genuine correlations or introduce spurious ones, negatively impacting model performance. Furthermore, balancing often fails to address the root cause of undesired dependencies, such as confounding or hidden stratification, leading to models that are neither fair nor robust. The interaction between data balancing and other mitigation techniques like regularization is also complex, with potential for negative interference. Therefore, a thorough understanding of the causal graph underlying the data is crucial before employing data balancing. Ignoring this can result in models that perform worse than models trained on unbalanced data, highlighting the need for a more nuanced and principled approach to data preprocessing for fair and robust AI.

Causal Graph Impact

#

The research paper section on “Causal Graph Impact” likely explores how causal relationships, represented in a causal graph, are affected by data balancing techniques. The authors probably demonstrate that naively balancing data without considering the causal structure can lead to unintended consequences. For instance, data balancing might remove statistical dependencies between variables, but not necessarily the underlying causal links. This can result in models that are sensitive to distributional shifts or fail to generalize well, even if they perform well on the balanced training data. The analysis likely highlights the importance of understanding the causal mechanisms that generate the data before applying data balancing. By analyzing the impact of data balancing on various parts of the causal graph, the paper possibly provides insights into when data balancing is effective and when it’s detrimental to fairness and robustness, emphasizing the necessity of a causal perspective for responsible data preprocessing.

Regularization Effects

#

Regularization techniques, often employed to enhance model generalizability and prevent overfitting, can interact in complex ways with data balancing strategies. The paper highlights that the effectiveness of regularization is contingent upon the data distribution. In scenarios where data balancing modifies the underlying causal relationships, applying regularization based on the original causal graph may not yield the desired results, potentially hindering the intended mitigation of undesired dependencies. A key insight is that the success of combined regularization and data balancing depends critically on the existence and nature of any causal links, and the presence of confounders. Therefore, a careful analysis of the causal structure of the data is vital before combining these methods, with the paper suggesting different approaches depending on whether the task is anti-causal or causal, and whether additional confounding variables are present. Failure to consider the interplay between these techniques could lead to unexpected and detrimental outcomes, emphasizing the need for a more nuanced understanding of their combined effects in the pursuit of fairness and robustness.

Failure Mode Analysis

#

A failure mode analysis for data balancing methods in machine learning would systematically explore scenarios where these techniques fail to improve fairness or robustness. Key failure modes include: the presence of unobserved confounders that influence both the sensitive attribute and the outcome, leading to spurious correlations that data balancing might reinforce; situations where the sensitive attribute and the outcome are entangled, making it impossible to disentangle them through re-weighting or re-sampling; and cases where data balancing inadvertently creates new undesired dependencies between variables. A comprehensive analysis would involve both theoretical investigation of causal relationships, and empirical evaluations on diverse datasets. The analysis should consider various data balancing techniques (re-weighting, oversampling, undersampling), different fairness or robustness criteria, and assess the interaction between data balancing and other mitigation methods like regularization or pre-processing. Understanding these failure modes is critical for responsible use of data balancing and the development of more robust and equitable machine learning models. The analysis would highlight conditions under which data balancing is likely to succeed or fail, providing practitioners with valuable insights for choosing appropriate data pre-processing strategies.

Future Research

#

The paper’s “Future Research” section would benefit from exploring several avenues. Expanding the causal framework to encompass more complex scenarios with multiple confounders and intricate relationships between variables is crucial. Investigating the interplay between data balancing and other mitigation techniques, such as algorithmic fairness constraints, in a unified framework would offer valuable insights. Developing a more nuanced understanding of disentanglement in model representations is needed—how does this impact fairness and robustness, and how can we effectively achieve disentanglement during model training? Extending the analysis beyond binary classification tasks to other types of predictive modeling problems is essential to establish the generalizability of the findings. Finally, a detailed exploration of the practical implications of the proposed conditions, including guidance on how to identify and address violations in real-world datasets, would strengthen the paper’s impact.

More visual insights

#

More on figures

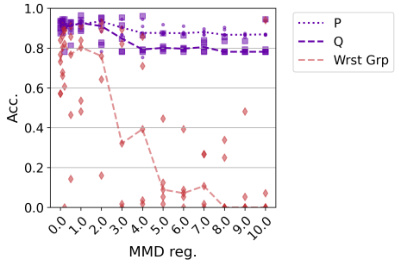
This figure shows the accuracy of models trained on two different distributions (Pt and Q) with varying levels of Maximum Mean Discrepancy (MMD) regularization, tested across different levels of confounding strength in the data. It illustrates how data balancing and regularization techniques interact to influence model performance and robustness in the presence of spurious correlations.

This figure displays the accuracy of models trained on balanced data for three different anti-causal tasks, evaluated on both their training distribution and a distribution (Pº) without the undesired dependency. The x-axis represents different values of the Maximum Mean Discrepancy (MMD) regularization hyperparameter. Each subfigure shows a different scenario: (left) purely spurious correlation; (middle) with an additional confounder; and (right) entangled signals. The red line indicates the worst group accuracy on Pº, highlighting the impact of balancing on fairness/robustness under different levels of regularization.

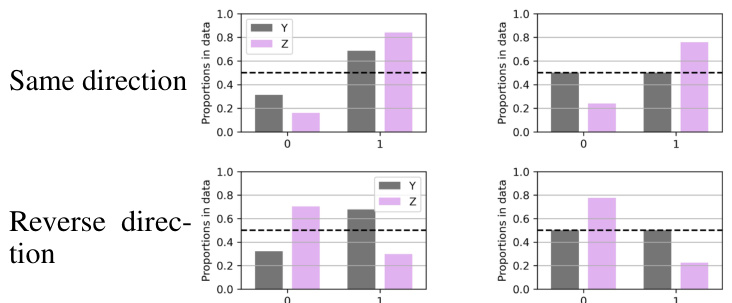
This figure shows the proportions of Y and Z before and after balancing the data on Y. It illustrates two scenarios: ‘same direction’, where the biases of Y and Z are in the same direction, and ‘reverse direction’, where the biases are in opposite directions. The figure demonstrates how data balancing on Y affects the marginal distribution of Z, potentially increasing bias in certain cases.

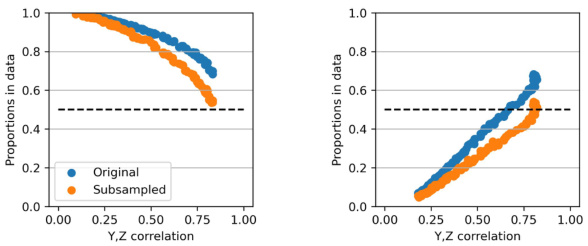
This figure shows the results of a simulation to illustrate how data balancing affects the marginal distribution of a binary sensitive attribute Z when the labels Y are balanced. The x-axis represents the correlation between Y and Z, while the y-axis shows the proportion of Z=1 in the dataset. Blue dots represent the original distribution, while orange dots show the distribution after balancing Y. The dashed line indicates a uniform distribution of Z (i.e., P(Z=1)=0.5). The left panel shows the case where Y and Z have similar biases, while the right panel shows the case with opposite biases. The results confirm that balancing Y can exacerbate the bias in Z if Y and Z have opposite biases.

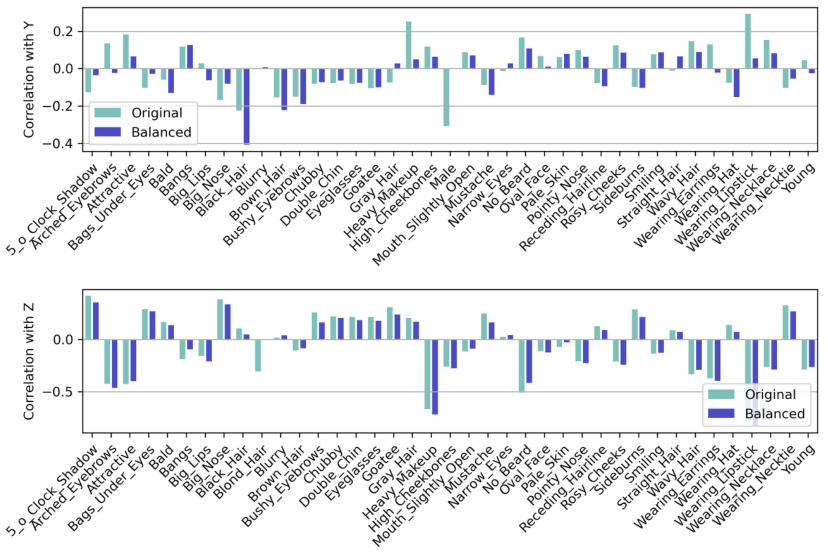
This figure displays the correlation between each attribute in the CelebA dataset and the target variable Y (helpfulness of review) and the sensitive attribute Z (gender), before and after data balancing. The teal bars represent the correlations in the original data, and the blue bars show the correlations after the data has been balanced. Comparing these correlations provides insight into how balancing the data affects the relationship between attributes and both the target and sensitive attribute.

More on tables

This table presents the performance of models trained on semi-synthetic data generated for four different scenarios (purely spurious correlation, additional confounder, entangled signals, and causal task with spurious correlation) depicted in Figure 1. The performance is evaluated on both the original training distribution (Pt) and a modified distribution (P0) where the undesired correlation is removed. The metrics reported are accuracy (Acc), worst-group accuracy (Worst Grp), confounder encoding (Encoding), and equalized odds (Equ. Odds). The arrows indicate whether higher or lower values are better for each metric.

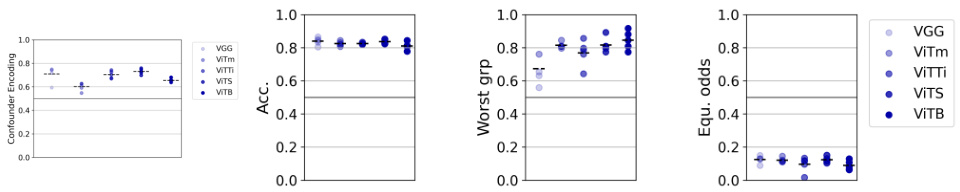
This table shows the performance of different models trained on the CelebA dataset. The models used are a VGG network and various sized Vision Transformers. The models were trained using either the original, imbalanced data (Pt), balanced data (Q), pre-trained on balanced data (Pre-trained on Q), or trained on imbalanced data with MMD regularization (MMD on Pt). The table reports accuracy, worst-group accuracy, confounder encoding, and equalized odds, all evaluated on the balanced dataset (Q). This allows for a comparison of the effect of different training methods on the performance and fairness of the models.

This table presents four causal Bayesian networks illustrating scenarios with undesired dependencies between Y and Z. Each scenario shows if data balancing leads to risk-invariant and/or optimal models. The impact of regularization strategies is also compared, suggesting next steps for each case.

Full paper

#