↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) algorithms often struggle with inaccurate value estimations due to incomplete data and the reliance on out-of-sample actions in the Bellman update. This leads to unstable optimization and suboptimal performance. Existing methods like double Q-learning attempt to mitigate this issue, but they face limitations in complex scenarios.
This paper introduces the Empirical MDP Iteration (EMIT) framework to enhance RL algorithms. EMIT constructs a sequence of simplified Markov Decision Processes (MDPs) from data in a replay memory, solving them iteratively. By restricting Bellman updates to in-sample actions, EMIT ensures that each simplified MDP converges to a unique optimal Q-function, improving overall stability and performance. Experimental results showcase the method’s effectiveness in reducing estimation errors and improving the performance of both Deep Q-Networks (DQN) and Twin Delayed Deep Deterministic policy gradients (TD3) across diverse benchmarks.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel approach to enhance reinforcement learning algorithms by addressing the common issue of estimation errors. The Empirical MDP Iteration (EMIT) framework provides a practical solution to improve the stability and performance of existing Q-learning methods, leading to better results in various domains. This is particularly relevant to researchers working with complex environments or limited data, where accurate value estimation is crucial for effective learning.
Visual Insights#
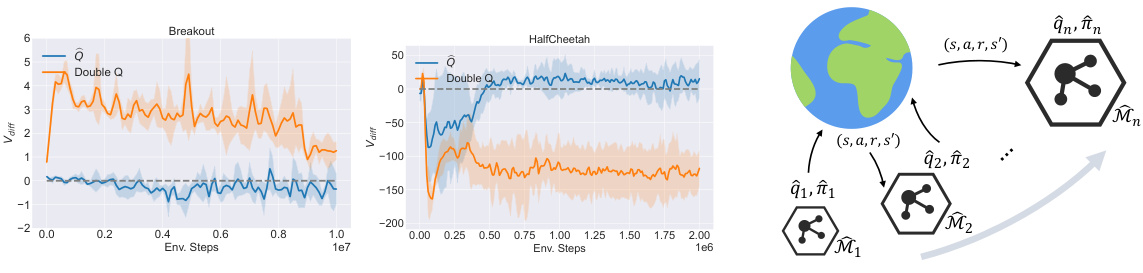
This figure compares the performance of the double Q-learning technique with an empirical Q-learning method on two tasks: Breakout and HalfCheetah. It also illustrates the Empirical MDP Iteration (EMIT) framework, which iteratively refines empirical MDPs using data from a replay memory to progressively approach the true MDP.

This table shows the hyperparameters used for the DQN algorithm in the Atari game experiments. It lists values for parameters such as batch size, replay memory size, target network update frequency, replay ratio, discount factor, optimizer, initial and final exploration rates, and the total number of steps in the environment.
In-depth insights#
Empirical MDP Iter#
The concept of “Empirical MDP Iteration” presents a novel approach to reinforcement learning by iteratively solving a sequence of empirical Markov Decision Processes (MDPs) derived from a replay buffer. Instead of directly tackling the complexity of the full MDP, this method incrementally refines its understanding of the environment, starting with a simplified MDP constructed from initial data and progressively expanding it as more experience is gained. This allows the agent to bootstrap from in-sample actions, dramatically reducing estimation errors stemming from the usual out-of-sample bootstrapping present in traditional Q-learning algorithms. Key to this method’s success is that each empirical MDP’s solution is guaranteed to be unique, given the limited, known transitions, paving the way for monotonic policy improvement. While the theoretical results show the method’s efficacy in tabular settings, the authors implement this within established online RL algorithms such as DQN and TD3. This is done through the use of a regularization and exploration method, using the solution of the empirical MDP to guide the learning and exploration in the original MDP. Ultimately, this offers a promising strategy for enhancing reinforcement learning algorithms, particularly in scenarios with incomplete or limited data.
In-sample Bellman#
The concept of “In-sample Bellman” in reinforcement learning focuses on refining Bellman updates by restricting bootstrapping to only in-sample data. This addresses the instability often seen in standard Q-learning, particularly when function approximation is used. By limiting the update to transitions already observed in the replay memory, the algorithm reduces the impact of out-of-sample estimations. This approach makes the algorithm more stable and robust. The method guarantees a unique optimal Q-function for the empirical Markov Decision Process (MDP), based on observed data, hence improving estimation accuracy. A key advantage is that as the replay memory grows and covers the state-action space, the estimates monotonically improve, converging to the original MDP’s optimal solution. This makes it a suitable technique for regularizing online reinforcement learning and improving the stability and accuracy of value-based methods. The core idea is to leverage the in-sample information reliably and effectively before expanding into the exploration of the full environment. The approach contrasts with standard methods that directly bootstrap from the complete MDP, which may lead to unstable optimization from incomplete or noisy data.
EMIT Algorithmics#
EMIT algorithmics presents a novel framework for enhancing reinforcement learning (RL) algorithms by leveraging replay memory more effectively. Instead of directly optimizing the Bellman equation over the entire state-action space, EMIT iteratively solves a sequence of empirical MDPs constructed from the replay memory. This approach addresses the challenge of incomplete data by focusing the Bellman update on in-sample transitions, which significantly reduces estimation errors. The framework’s strength lies in its ability to seamlessly integrate with existing RL algorithms. By employing in-sample bootstrapping, EMIT ensures that each empirical MDP has a unique optimal Q-function, leading to a monotonic policy improvement. EMIT also incorporates a regularization term and an exploration bonus to enhance convergence and exploration. Experimental results demonstrate substantial performance improvements across various Atari and MuJoCo benchmark tasks. This highlights the power of exploiting replay memory before extensive environment exploration, a strategy with implications for sample efficiency and algorithm stability in RL.
Atari & MuJoCo Res#
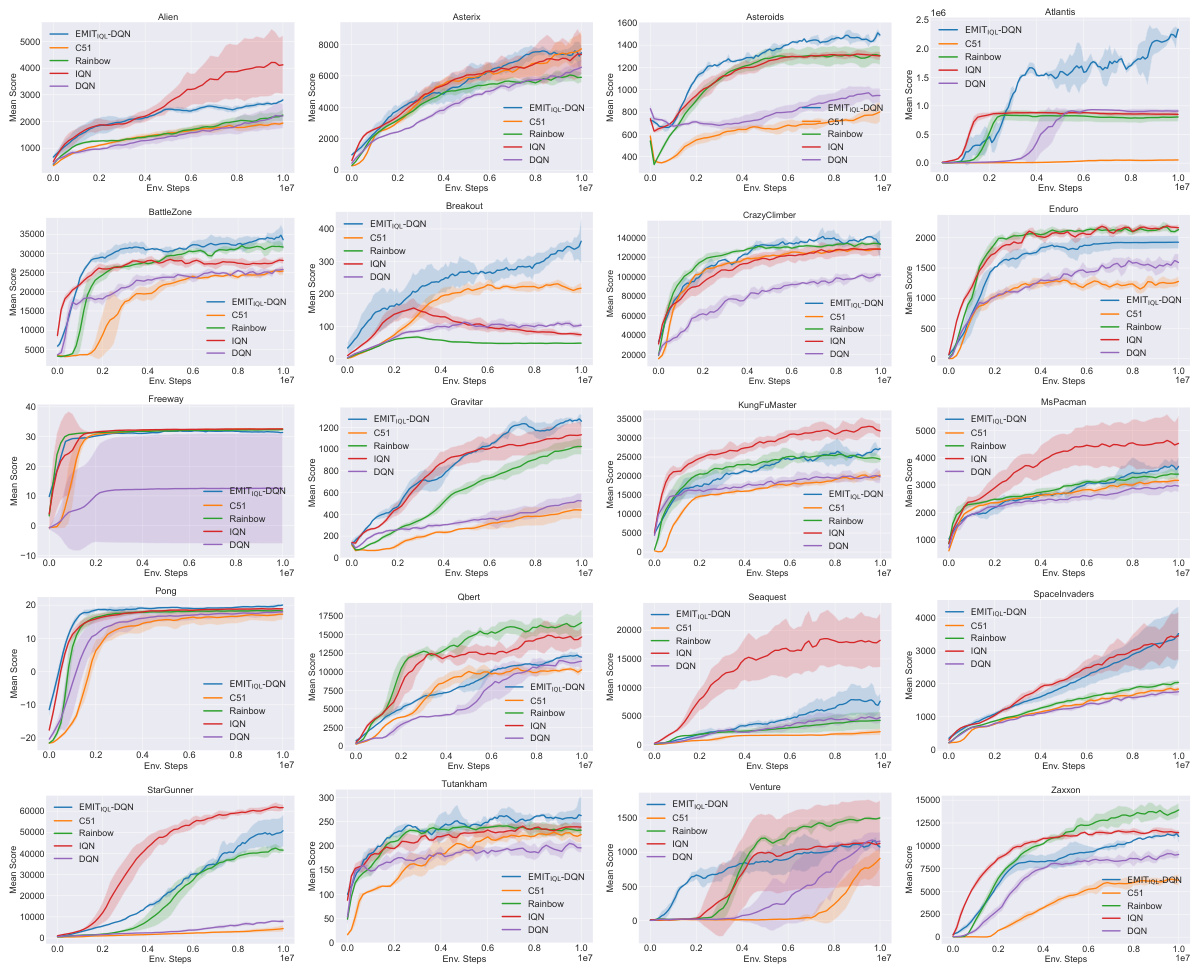
The heading “Atari & MuJoCo Res” likely refers to a section presenting results from experiments conducted on Atari and MuJoCo environments, two popular benchmarks in reinforcement learning. Atari games present a discrete action space challenge, emphasizing the ability of the algorithm to master complex visual inputs and strategic decision-making. MuJoCo, on the other hand, involves continuous control tasks, requiring fine-tuned control policies in simulated physics environments. The results in this section would likely demonstrate the performance of a novel algorithm or modification against established baselines on various Atari games and MuJoCo tasks. A strong presentation would showcase significant performance gains across diverse environments, highlighting the algorithm’s generalizability and robustness. Key metrics to expect include average scores, standard deviations across multiple runs, and potentially learning curves illustrating the rate of convergence. Further analysis might compare the algorithm’s performance against other state-of-the-art methods using normalized scores to account for task difficulty. The discussion should also analyze what aspects of the algorithm contribute to the observed improvements, potentially linking them to specific characteristics of the Atari and MuJoCo environments. Finally, any limitations of the approach, such as computational cost or specific requirements, could also be discussed.
Future Work#
Future research directions stemming from this paper could explore several avenues. Extending EMIT’s applicability to a wider range of RL algorithms beyond DQN and TD3 is crucial to solidify its generalizability and impact. Investigating the optimal balance between exploration and exploitation within the EMIT framework warrants further investigation. Developing theoretical guarantees for EMIT’s convergence in non-tabular settings and continuous action spaces is also highly desirable, providing firmer mathematical grounding. A comparative analysis of EMIT against other offline RL techniques would illuminate its unique strengths and limitations. Finally, empirical evaluations on more complex and realistic environments, along with a deeper examination of the impact of EMIT on sample efficiency, would provide valuable insights for practical applications.
More visual insights#
More on figures

This figure shows an example in CliffWalk environment with four different scenarios of replay memory content. The first row visualizes the state-action pairs present in each replay memory. The second row shows the estimation error curves for Q and Q (learned using Bellman update and in-sample Bellman update respectively) compared to the true optimal Q*. The third and fourth rows illustrate the resulting greedy policies derived from Q and Q respectively, with red arrows highlighting incorrect actions.
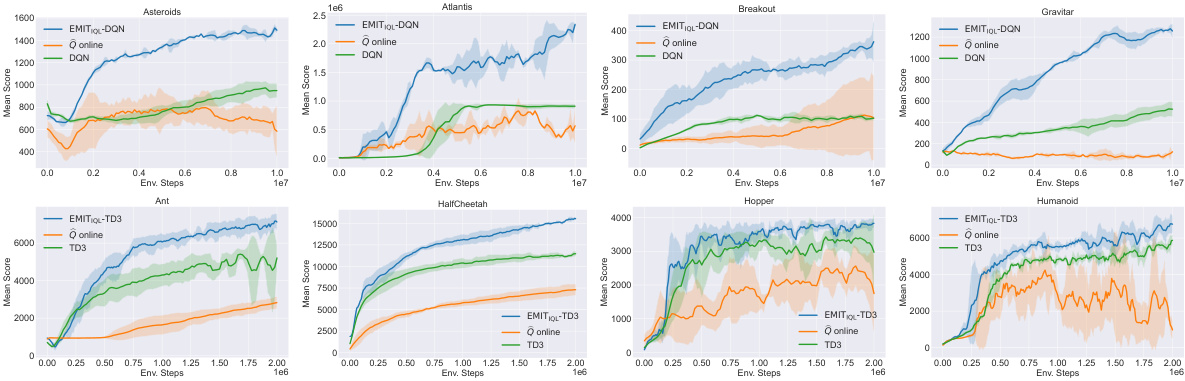
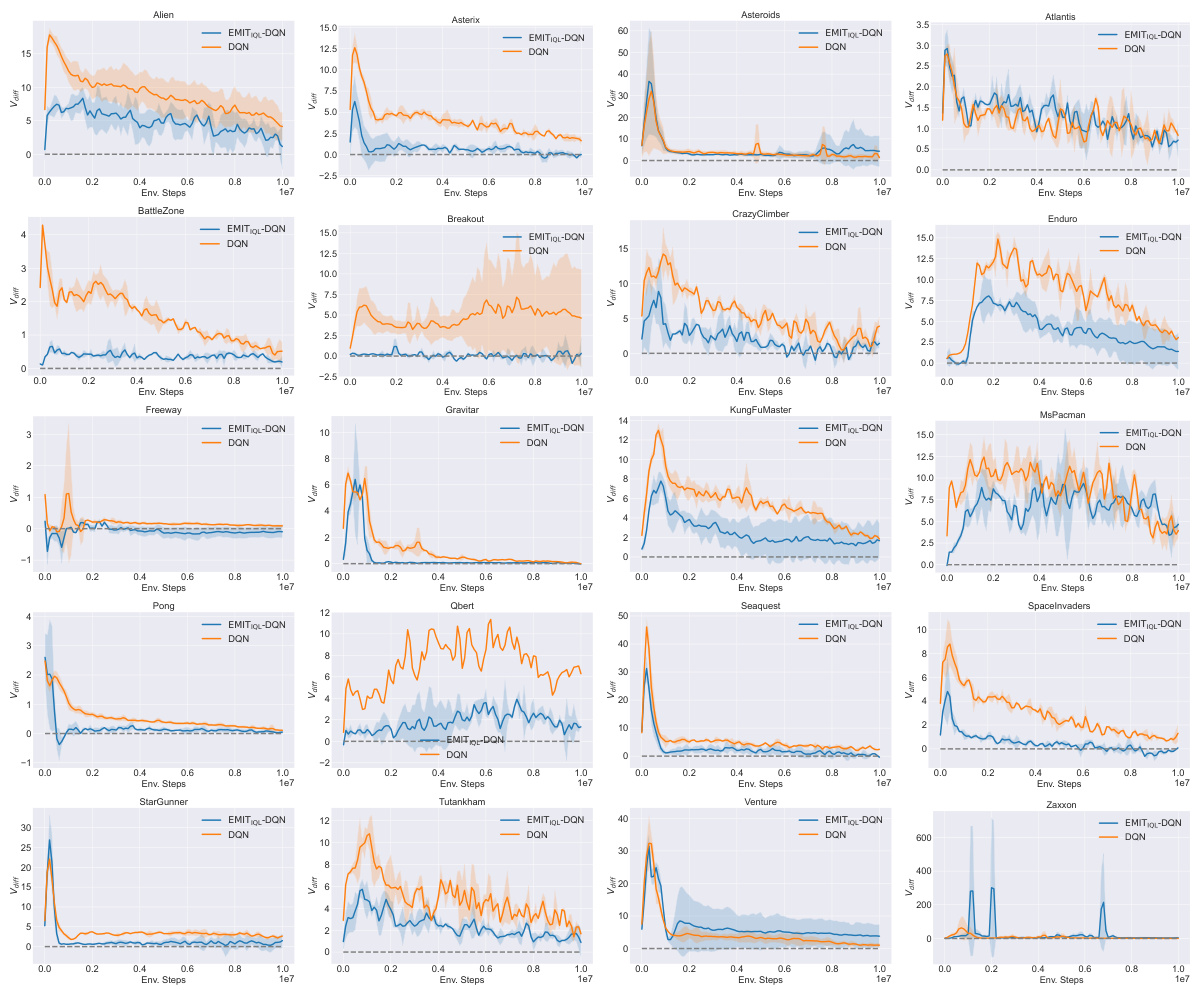
This figure displays the learning curves for several Atari and MuJoCo reinforcement learning tasks. The top row shows results for Atari games (Asteroids, Atlantis, Breakout, Gravitar), while the bottom row presents results for MuJoCo continuous control tasks (Ant, HalfCheetah, Hopper, Humanoid). Each curve represents the average performance across five independent runs, with shaded areas indicating standard deviation. The results demonstrate that incorporating the Empirical MDP Iteration (EMIT) method consistently improves performance compared to standard DQN and TD3 algorithms across various environments.
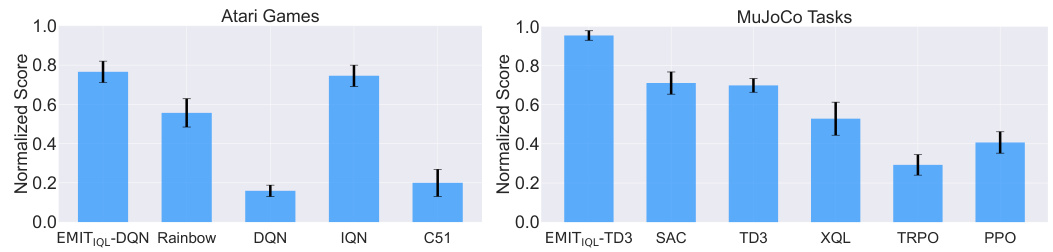
This figure compares the average normalized performance of different reinforcement learning algorithms across 20 Atari games and 8 MuJoCo tasks. The normalization ensures scores are between 0 and 1, allowing for easy comparison. The results show that the Empirical MDP Iteration (EMIT) method consistently outperforms other state-of-the-art algorithms, demonstrating its effectiveness in improving the performance of both discrete and continuous control tasks.

This figure compares the performance of policies learned using the Bellman update (π) and the in-sample Bellman update (ŵ) on Breakout and HalfCheetah environments. The left plot (a) shows that the passive learning policy (ŵ) performs comparably or even better than the active learning policy (π), highlighting that the in-sample Bellman update is robust to missing transitions. The right plot (b) demonstrates that EMIT significantly reduces the estimation error in Q, leading to more accurate value estimations.

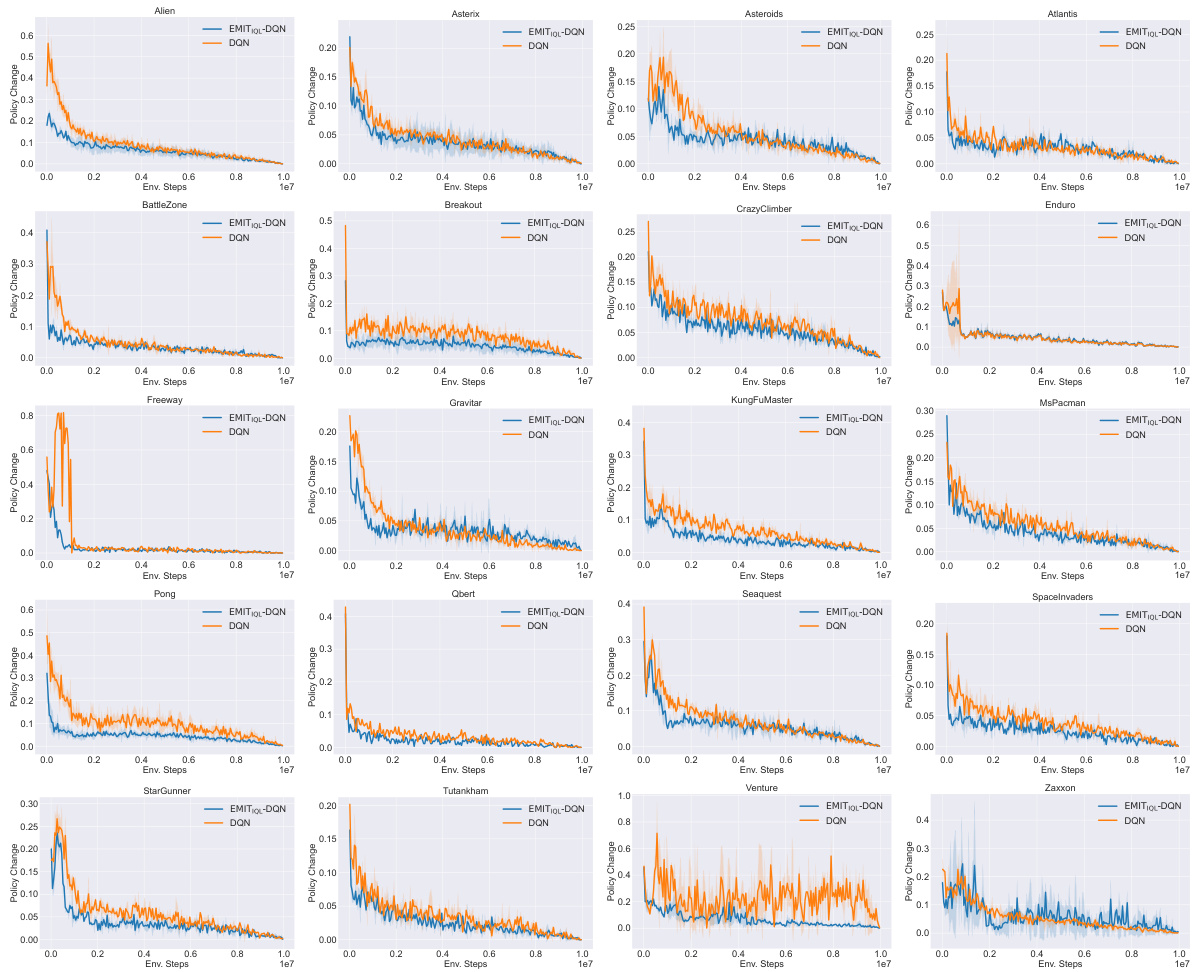
This figure shows an ablation study on the effects of the regularization term and exploration bonus in the proposed EMIT method. The left panel (a) illustrates how EMIT reduces policy churn (frequent changes in the optimal policy) compared to a standard DQN. The right panel (b) displays the performance improvement when using the full EMIT method versus versions without regularization, without the exploration bonus, and without both components. This demonstrates that both components contribute to performance, and the regularization term is more impactful than the exploration bonus.
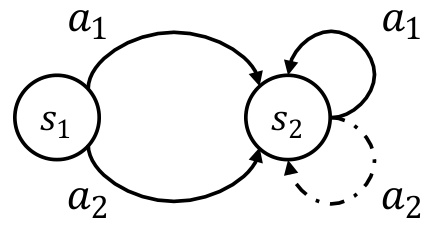
This figure shows a simple Markov Decision Process (MDP) with two states (s1, s2) and two actions (a1, a2). The solid lines represent transitions that are present in the replay memory, while the dashed line represents a transition that is missing. The absence of the (s2, a2) transition highlights the concept of incomplete data within a replay memory, which is central to the paper’s discussion of the limitations of the standard Bellman update in reinforcement learning. The missing transition impacts the accuracy of value estimation and policy learning, especially when using the standard Bellman update which bootstraps from out-of-sample actions.

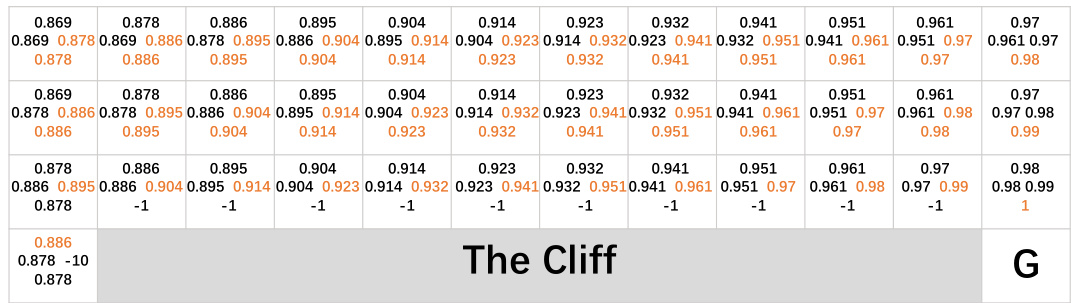
This figure illustrates the CliffWalking environment. It’s a grid world where the agent starts at the bottom left (S) and must navigate to the goal state (G) at the bottom right. A shaded region represents a ‘cliff,’ which results in a large negative reward if the agent steps into it. The arrow shows the optimal path for the agent to take to reach the goal while avoiding the cliff, highlighting the risk of falling and receiving a negative reward. The purpose of the figure is to provide a simple visual representation of the environment used in the paper’s experiments.
This figure shows a comparison between two Q-learning methods (Bellman update and in-sample Bellman update) applied to CliffWalk in four different scenarios with varying levels of data coverage. It shows that in-sample Bellman update provides more robust estimations and yields more accurate policies, especially in scenarios with incomplete data.

This figure shows screenshots of five different Atari 2600 games used in the experiments described in the paper. These games represent a diversity of gameplay mechanics and visual styles, allowing the researchers to evaluate the performance of their reinforcement learning method across a range of challenges.
This figure shows visualizations of five different MuJoCo environments used in the paper’s experiments: Ant, HalfCheetah, Hopper, Swimmer, and Walker2D. These are simulated robotic control tasks, each with a distinct morphology and locomotion style, used to evaluate the performance of reinforcement learning algorithms. The environments are rendered in a simple, checkered-floor setting.

This figure shows a comparison of the performance of in-sample and out-of-sample Bellman updates in the CliffWalk environment. Four scenarios with varying data coverage are shown, highlighting how the in-sample approach is more robust to incomplete data. The figure displays the learning curves, value errors, and resulting policies for both methods, demonstrating the superior performance of the in-sample Bellman update when dealing with incomplete data.

This figure displays the performance of DQN and TD3 algorithms with and without the EMIT enhancement on Atari and MuJoCo benchmark tasks. Learning curves show mean scores with standard deviation across 5 runs for each task. The results clearly indicate consistent performance improvements across diverse tasks when EMIT is applied.
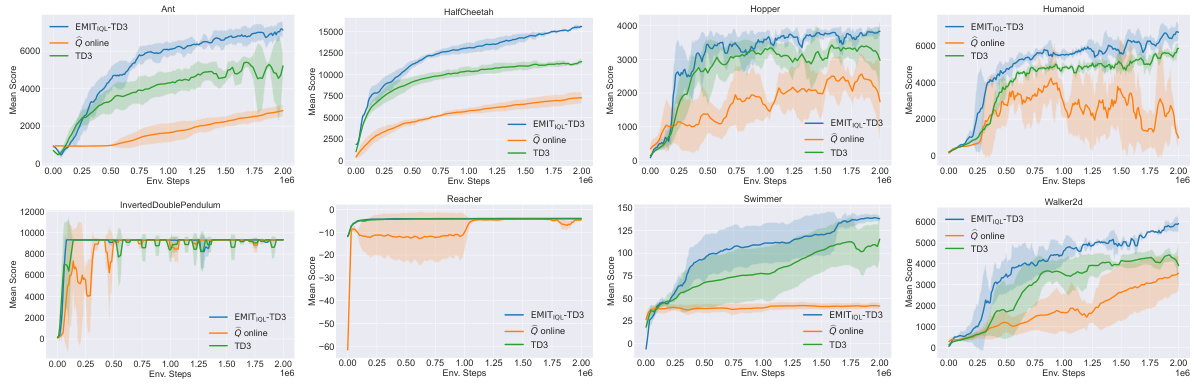
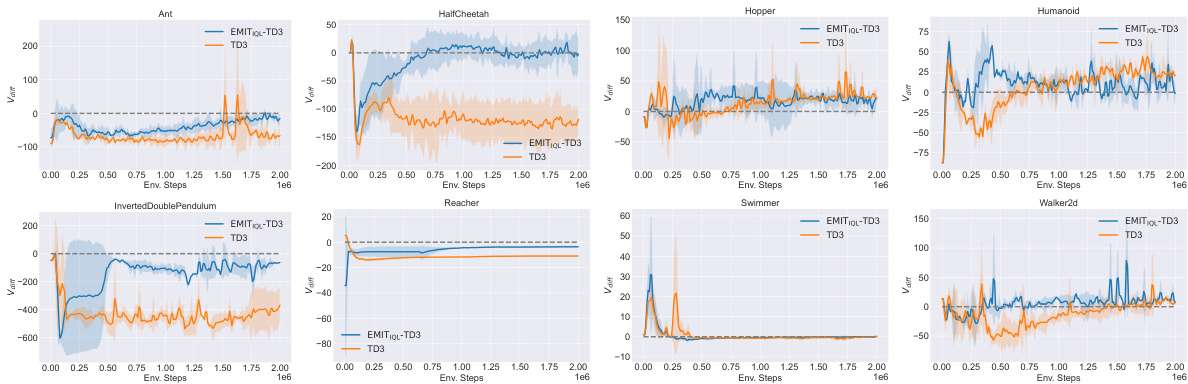
The figure shows the learning curves for eight MuJoCo continuous control tasks. The curves compare the performance of three different methods: EMIT-TD3 (the proposed method combining Empirical MDP Iteration with TD3), TD3 (the baseline TD3 algorithm), and Q_online (a TD3 variant using only in-sample Bellman updates but lacking the exploration component of EMIT). The shaded areas represent the standard deviation across five runs. The results illustrate that EMIT-TD3 consistently outperforms both TD3 and Q_online across all tasks, demonstrating the effectiveness of the proposed method in improving the performance of existing reinforcement learning algorithms.
The figure presents learning curves for DQN and TD3 algorithms, with and without the EMIT enhancement, across various Atari and MuJoCo environments. It showcases the consistent performance improvement achieved by integrating EMIT into both algorithms across diverse tasks, highlighting the method’s effectiveness. Each curve represents the average performance over five independent runs, with shaded regions indicating standard deviations. The x-axis represents the number of environment steps, and the y-axis represents the mean score achieved.

This figure displays the results of applying the Empirical MDP Iteration (EMIT) method to Deep Q-Network (DQN) and Twin Delayed Deep Deterministic policy gradient (TD3) algorithms on Atari and MuJoCo benchmark tasks. The top row shows results for several Atari games (Asteroids, Atlantis, Breakout, Gravitar), while the bottom row shows results for several MuJoCo continuous control tasks (Ant, HalfCheetah, Hopper, Humanoid). Each plot presents the mean reward over five independent runs, along with the standard deviation represented by shaded areas. The results demonstrate that EMIT consistently improves the performance of both DQN and TD3 across all tested environments.

The figure shows the performance comparison of the proposed EMIT method against baseline methods (DQN and TD3) across various Atari and MuJoCo environments. The learning curves illustrate the mean scores and standard deviations across five independent runs. The results demonstrate that EMIT consistently improves performance in a variety of tasks.

This figure displays the learning curves for both Atari and MuJoCo environments. The top row shows results from Atari games, while the bottom row shows results from MuJoCo continuous control tasks. Each environment’s performance is shown as a learning curve, plotting mean score against environment steps. Shaded regions indicate standard deviation across five runs. The results clearly demonstrate that using EMIT consistently improves the learning performance compared to using standard DQN and TD3.

This figure displays the performance of the proposed EMIT method compared to standard DQN and TD3 algorithms on both Atari and MuJoCo benchmark tasks. The learning curves show the average reward obtained over five independent runs, illustrating the consistent performance improvement provided by EMIT across various game and robotic control environments. Error bars represent standard deviations, showcasing the stability of EMIT’s performance enhancements.
The figure shows the learning curves for DQN and TD3 algorithms on Atari and MuJoCo environments with and without EMIT. The results demonstrate that incorporating EMIT significantly improves performance across a variety of tasks, both discrete and continuous control tasks. The graphs display mean scores and standard deviations across five independent runs, illustrating the consistency of EMIT’s performance enhancement.
This figure displays the performance of DQN and TD3 algorithms with and without the EMIT enhancement on various Atari and MuJoCo benchmark tasks. Each plot shows the mean reward over five independent runs, with error bars representing the standard deviation. The results clearly demonstrate that integrating EMIT significantly improves the learning performance and stability of both DQN and TD3 across a range of tasks with different complexities and action spaces (discrete for Atari, continuous for MuJoCo).
This figure compares the performance of two Bellman updates (Eqs. 1 and 2) on a CliffWalk environment. The left panel shows the estimation errors when the replay memory contains either a suboptimal trajectory or is missing transitions. The right panel shows the resulting policies, highlighting the differences in accuracy between the two methods.

This figure displays the learning curves for both Atari and MuJoCo environments. Each curve represents the average performance across five runs, with shaded areas indicating standard deviation. The results demonstrate that using EMIT consistently improves the performance compared to the baselines across multiple environments, showing its effectiveness in enhancing reinforcement learning algorithms.

This figure displays the learning curves for both Atari and MuJoCo benchmark tasks. Each curve represents the mean score across five runs of each algorithm, with shaded areas indicating standard deviations. The results demonstrate that the EMIT method consistently outperforms the baseline algorithms (DQN and TD3) across a variety of tasks, showcasing its effectiveness in enhancing reinforcement learning performance.
More on tables
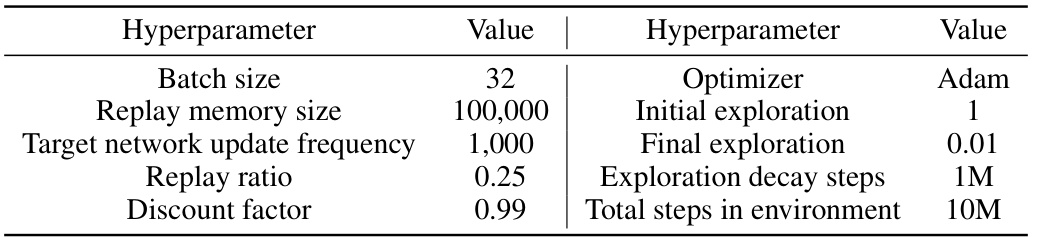
This table lists the hyperparameters used for the Deep Q-Network (DQN) algorithm when applied to Atari game environments. It specifies values for key parameters such as batch size, replay memory size, target network update frequency, replay ratio, discount factor, optimizer, initial and final exploration rates, exploration decay steps, and the total number of steps in the environment during training.
This table lists the hyperparameters used for the TD3 algorithm on MuJoCo environments. It shows the values used for batch size, replay memory size, discount factor, optimizer, learning rate, target update rate, policy noise, noise clip, delayed policy update frequency, and total steps in the environment. These parameters are crucial for the training and performance of the TD3 algorithm.
Full paper#



















