Risk-sensitive control as inference with Rényi divergence

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in reinforcement learning and optimal control because it unifies existing frameworks, offers novel risk-sensitive RL algorithms, and bridges the gap between control theory and Bayesian inference. The findings advance risk-sensitive control, offering robust and efficient methods for solving complex problems.

Visual Insights

#

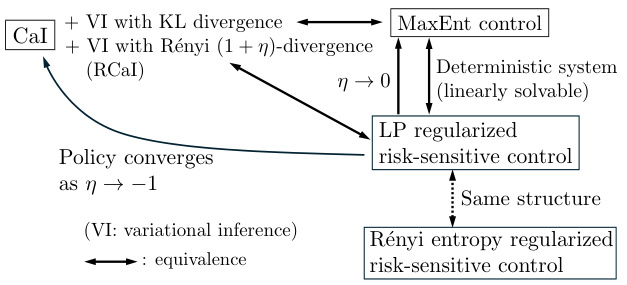
This figure summarizes the relationships between several control problems discussed in the paper. It shows the equivalence between Control as Inference (CaI) with KL divergence and MaxEnt control. It illustrates how CaI with Rényi divergence (RCaI) extends CaI and connects to LP regularized risk-sensitive control. As the risk-sensitivity parameter (η) approaches 0, RCaI converges to MaxEnt control. As η approaches -1, the policy converges. A parallel risk-sensitive generalization using Rényi entropy regularization is also shown, demonstrating the same structure as the LP regularized approach.

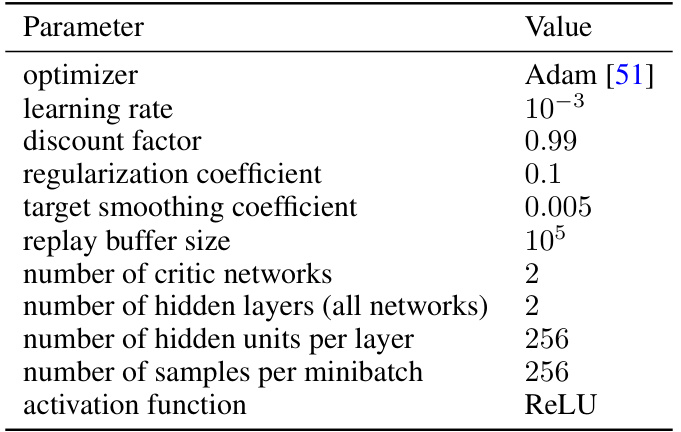
This table lists the hyperparameters used for both the Soft Actor-Critic (SAC) and the Risk-Sensitive Soft Actor-Critic (RSAC) algorithms. It includes the optimizer used (Adam), learning rate, discount factor, regularization coefficient, target smoothing coefficient, replay buffer size, number of critic networks, number of hidden layers and units per layer in the networks, the number of samples per minibatch, and the activation function used (ReLU). These hyperparameters are crucial for the performance and stability of both algorithms.

In-depth insights

#

Risk-Sensitive CAI

#

Risk-sensitive control as inference (RCaI) offers a novel approach to unify and extend existing control frameworks. By incorporating Rényi divergence in the variational inference process, RCaI elegantly bridges the gap between risk-neutral and risk-sensitive control paradigms. This is achieved by demonstrating its equivalence to log-probability regularized risk-sensitive control, a generalization of maximum entropy control. A key advantage lies in its ability to derive risk-sensitive reinforcement learning algorithms (policy gradient and soft actor-critic) through minor modifications to their risk-neutral counterparts. Furthermore, RCaI reveals a soft Bellman equation, offering valuable insights into the nature of the optimal policies and their connections to linearly solvable control. The framework’s flexibility is highlighted by an alternative risk-sensitive generalization using Rényi entropy regularization, illustrating the robustness of its core structure. However, limitations exist, particularly regarding numerical instability for certain risk-sensitivity parameters and scalability to large-scale problems. Future research should focus on addressing these limitations and exploring the practical implications of this unifying approach.

Rényi Divergence RL

#

Rényi Divergence Reinforcement Learning (RL) offers a powerful generalization of standard RL methods by incorporating Rényi divergence, a flexible measure of dissimilarity between probability distributions. Instead of relying solely on the Kullback-Leibler (KL) divergence, as in many maximum entropy RL approaches, Rényi divergence allows for adjustable risk sensitivity. This means the agent’s behavior can be tuned to be more risk-averse or risk-seeking, which is particularly useful in scenarios with uncertain rewards or environments. The parameter ‘alpha’ in Rényi divergence controls this risk sensitivity; values of alpha less than 1 favor exploration and risk-seeking, while values greater than 1 promote exploitation and risk aversion. A significant advantage of this approach is its ability to unify various RL algorithms under a single theoretical framework, highlighting the connections between seemingly disparate methods. The resulting algorithms often exhibit improved robustness and faster convergence compared to traditional KL-based methods. However, challenges remain, particularly in managing the computational complexity associated with Rényi divergence and ensuring the stability of learning across different values of alpha. Therefore, further research is necessary to fully exploit the potential of this exciting approach in diverse and challenging RL applications.

Soft Bellman Eq.

#

The concept of a “Soft Bellman Equation” represents a significant departure from the traditional Bellman equation in reinforcement learning. The standard Bellman equation provides a recursive relationship for calculating the optimal value function, crucial for finding optimal policies. However, it often struggles with complex state spaces and stochasticity. The “soft” modification introduces an entropy term, promoting exploration and preventing convergence to suboptimal deterministic policies. This entropy regularization results in a smoother, more robust value function and ultimately, a more diverse and potentially better policy. The soft Bellman equation fundamentally alters the optimization landscape, trading off immediate reward maximization with policy diversity and long-term stability. Its implications are profound, impacting algorithm design, theoretical analysis, and the overall effectiveness of reinforcement learning methods, particularly in challenging environments. Solving the soft Bellman equation often involves numerical approximations or iterative methods due to its inherent complexity, but the resulting policies exhibit valuable properties like robustness and adaptability, making it a key component of maximum entropy reinforcement learning.

Policy Gradient

#

Policy gradient methods are a cornerstone of reinforcement learning, offering a direct approach to optimizing policies. Instead of optimizing a value function, policy gradients directly update the policy parameters to improve performance. A key advantage is their ability to handle stochastic policies, enabling exploration and potentially escaping local optima. However, high variance in the gradient estimates can hinder convergence, making techniques like baseline functions and variance reduction essential. The choice of policy parameterization significantly influences efficiency and the capacity to scale to complex problems. Further advancements involve entropy regularization to encourage exploration and address the issue of deterministic policies getting stuck in local minima. While widely applicable, the computational demands for high-dimensional problems remain a concern. Therefore, research continues to explore novel techniques to stabilize gradient estimation and improve sample efficiency.

Future Directions

#

Future research could explore several promising avenues. Extending the risk-sensitive control framework to more complex scenarios, such as partially observable environments or those with continuous state and action spaces, is crucial. Developing more efficient and stable algorithms for risk-sensitive reinforcement learning, particularly for high-dimensional problems, is a key challenge. Investigating the impact of different risk-sensitivity parameters and their effect on exploration-exploitation trade-offs requires further study. Theoretical analysis of the convergence properties of risk-sensitive RL algorithms and the development of tighter performance bounds would significantly advance the field. Finally, applications to real-world problems that demand risk-sensitive decision making, such as robotics, finance, and healthcare, should be prioritized to demonstrate the practical value of this framework.

More visual insights

#

More on figures

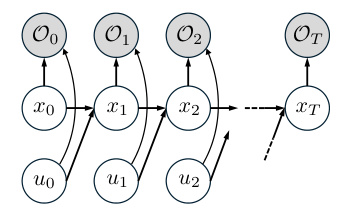
This figure shows a graphical model representation of Control as Inference (CaI). It illustrates the relationships between the states (x), control inputs (u), and optimality variables (O) over a time horizon T. Each time step t has a state variable xt, a control input ut, and an optimality variable Ot. The optimality variable Ot indicates whether (xt, ut) is optimal or not. The arrows represent the conditional dependencies: the next state xt+1 depends on the current state xt and the control input ut; and the optimality variable Ot depends on the current state xt and control input ut.

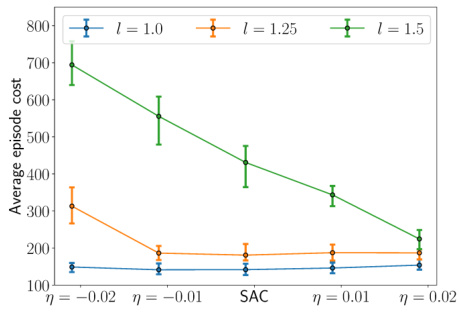
This figure shows the average episode cost for the risk-sensitive soft actor-critic (RSAC) algorithm with different values of the risk-sensitivity parameter η, compared to the standard soft actor-critic (SAC) algorithm. The experiment was conducted using the Pendulum-v1 environment from OpenAI Gym. The results demonstrate the impact of the risk-sensitivity parameter on the average episode cost and highlight the robustness of RSAC against perturbations in the environment (changes in pendulum length).

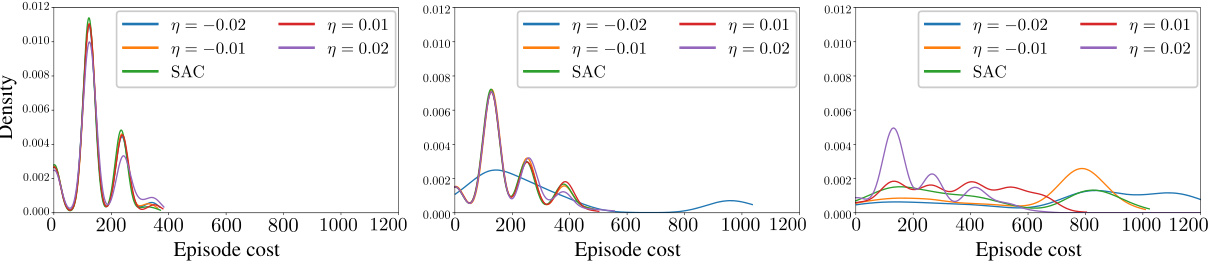
This figure shows the empirical distributions of episode costs for different risk-sensitivity parameters (η) in the Pendulum-v1 environment. Three subplots represent different pendulum lengths (l): the original length (l=1.0) used during training, and perturbed lengths (l=1.25 and l=1.5). Each subplot displays distributions for various η values (including η=0 for standard SAC), illustrating the impact of risk sensitivity on cost distribution under system perturbations. The distributions are obtained from 20 independent training runs, each with 100 sampling paths for cost calculation.

This figure shows the training curves for the risk-sensitive soft actor-critic (RSAC) algorithm with different values of the risk-sensitivity parameter η, along with a standard soft actor-critic (SAC) algorithm. The x-axis represents the number of learning steps, and the y-axis represents the average episode cost. The shaded regions represent the standard deviation of the results. The plot demonstrates how the choice of risk-sensitivity affects the learning process and the final performance of the algorithm.

Full paper

#