↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat
TL;DR#
Current graph generative models struggle to handle all types and levels of graph learning tasks simultaneously, often failing to generate structures and features at once or limiting themselves to specific task types. Existing methods also lack theoretical guarantees for tasks beyond generation.
This research introduces Latent Graph Diffusion (LGD), a novel framework that overcomes these limitations. LGD formulates all graph learning tasks (node, edge, and graph-level; generation, regression, and classification) as conditional generation, enabling diffusion models to address them with provable guarantees. LGD uses a pretrained encoder-decoder to embed graph data into a continuous latent space, where a powerful diffusion model is trained. Extensive experiments show LGD achieves state-of-the-art or competitive results on various graph learning tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents Latent Graph Diffusion (LGD), the first unified framework for graph learning. This addresses a critical gap in current research by handling all levels (node, edge, graph) and types (generation, regression, classification) of tasks with high performance. It also provides theoretical guarantees, opening doors for future research in foundation models for graph data and advancing applications across various domains.
Visual Insights#
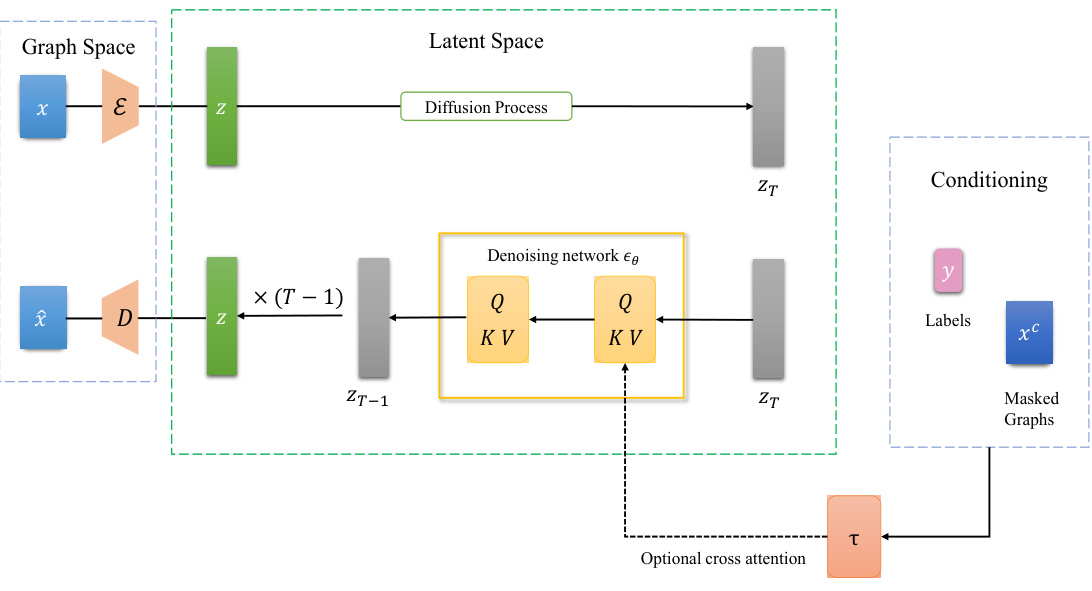
🔼 The figure illustrates the architecture of the Latent Graph Diffusion (LGD) framework. It shows how the framework takes graph data as input, encodes it into a latent space using an encoder (E), applies a diffusion process to the latent representation, and then decodes it back into the graph space using a decoder (D). The framework is capable of performing both generation and prediction tasks. The optional cross-attention mechanism allows for conditional generation, enabling control over the generated graph by providing additional information.
read the caption
Figure 1: Illustration of the Latent Graph Diffusion framework, which is capable of performing both generation and prediction.
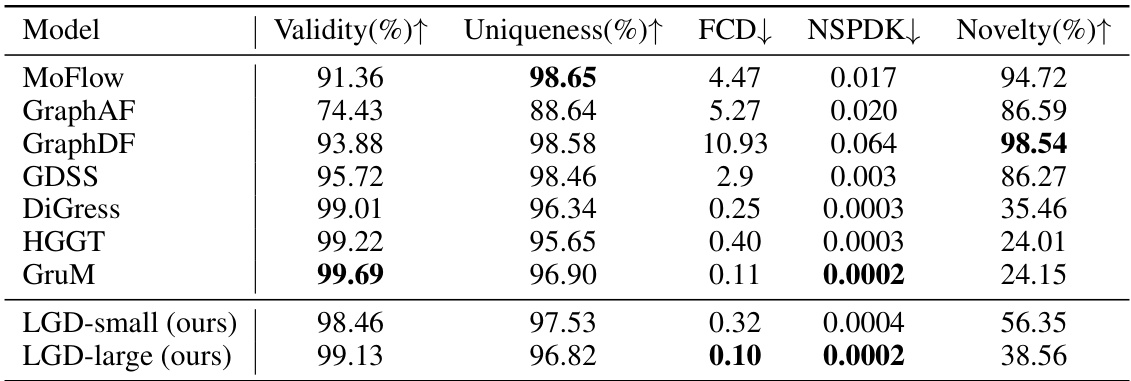
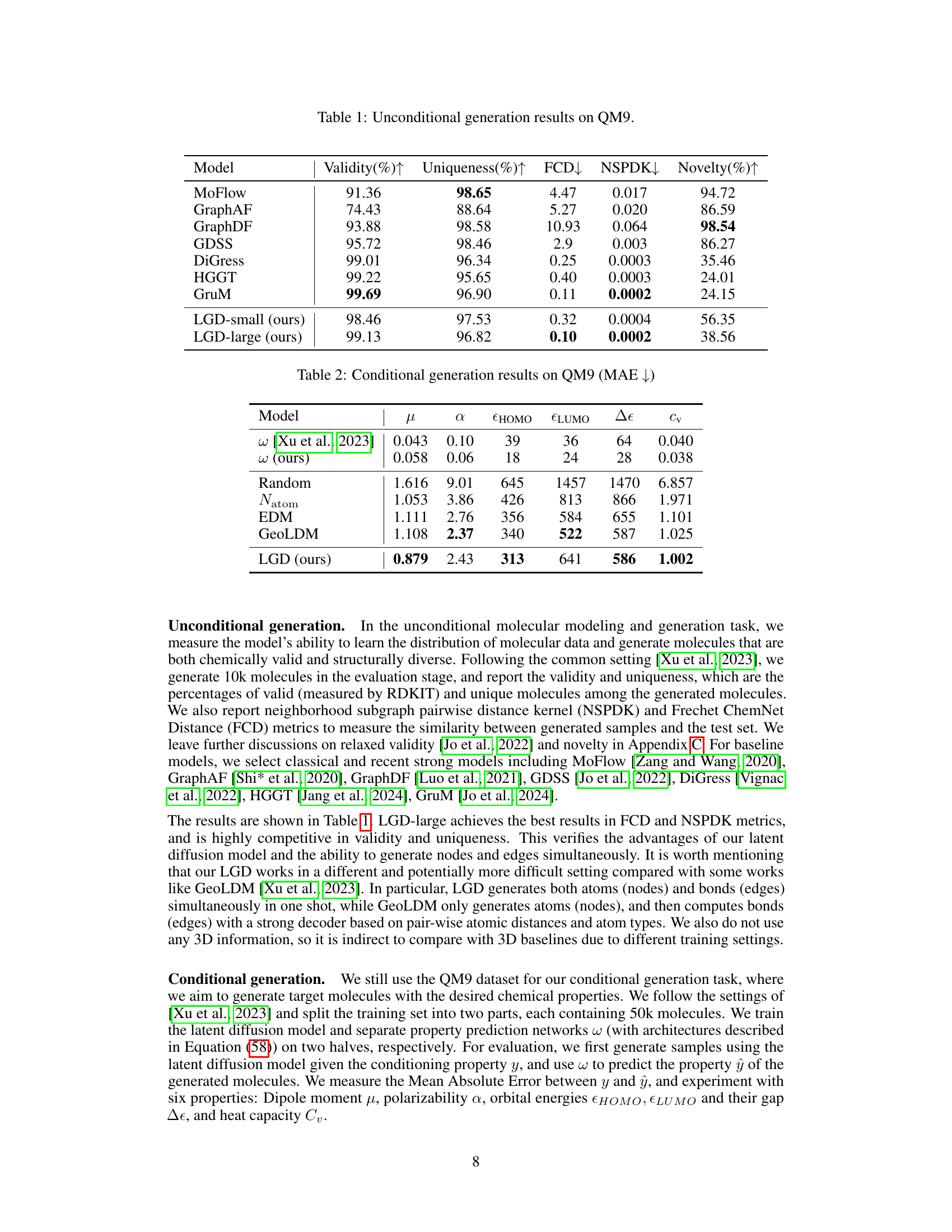
🔼 This table presents the results of unconditional molecular generation experiments using the QM9 dataset. Several metrics are used to evaluate the performance of different models, including Validity (percentage of chemically valid molecules), Uniqueness (percentage of unique molecules), FCD (Fréchet ChemNet Distance, measuring similarity to the test set), NSPDK (Neighborhood Subgraph Pairwise Distance Kernel, another similarity metric), and Novelty (percentage of novel molecules). The results show how well each model generates molecules that are both chemically valid and structurally diverse, and how similar those molecules are to the molecules in the test set.
read the caption
Table 1: Unconditional generation results on QM9.
In-depth insights#
Latent Graph Diffusion#
The concept of “Latent Graph Diffusion” presents a novel approach to graph-based machine learning. By embedding graph structures and features into a latent space, it leverages the power of diffusion models for both generative and predictive tasks. This unified framework allows for solving tasks at all levels (node, edge, graph) and all types (generation, regression, classification), overcoming limitations of previous methods that handled these tasks separately. The use of a latent space is crucial, mitigating challenges posed by discrete graph structures and diverse feature types. The model’s success hinges on a powerful encoder-decoder architecture which enables simultaneous generation of structures and features, and a diffusion model trained within that latent space. The method’s theoretical underpinnings are grounded in reformulating prediction tasks as conditional generation problems. Empirical results suggest a state-of-the-art or highly competitive performance. Further exploration of the latent space, particularly its properties and dimensionality, is necessary to fully understand its implications for various applications.
Unified Task Model#
A unified task model in machine learning aims to create a single framework capable of handling diverse learning tasks. This approach contrasts with traditional methods that usually require separate models for each task type (e.g., classification, regression, generation). A key advantage is efficiency: training and deploying one model is simpler than managing multiple specialized ones. However, a unified model needs to address the complexities arising from different task structures and data types. This necessitates careful design choices, such as the use of a shared latent representation or a flexible architecture that adapts to different task demands. A potential drawback is reduced performance: a generalist model might not achieve the specialized performance of dedicated models. Careful evaluation and comparison are therefore crucial to ensure the unified model’s effectiveness in a wide range of tasks. The success of such a model hinges on finding the right balance between generality and specialization, leading to a robust and efficient approach to machine learning.
Conditional Generation#
Conditional generation, in the context of this research paper, is a crucial technique that significantly extends the capabilities of the proposed Latent Graph Diffusion (LGD) model. By framing both regression and classification tasks as conditional generation problems, the researchers elegantly unify these seemingly disparate tasks under a single generative framework. This unification is achieved by conceptually treating the prediction of labels (y) as the generation of these labels conditioned on the input data (x). This approach allows the LGD model, designed for graph generation, to effectively handle both generative and deterministic graph-learning tasks. The use of a pretrained graph encoder to embed graph structures and features into a continuous latent space is a key component which enhances the performance of the diffusion model for tasks that deal with the discrete nature of graph data. Further bolstering this approach is the theoretical analysis that provides generalization bounds for the conditional latent diffusion model, establishing provable guarantees. The ability of the LGD model to incorporate the condition (x) through a specially designed cross-attention mechanism allows for controllable generation and offers a powerful mechanism for solving various prediction tasks. The overall approach significantly improves the versatility and applicability of the LGD model in tackling a wide range of graph-learning challenges.
Experimental Results#
The heading ‘Experimental Results’ in a research paper warrants a thorough analysis. A strong section will meticulously detail experimental setup, including datasets, evaluation metrics, and baseline models. Clear descriptions of the methodologies used, along with comprehensive tables and figures, are critical. The presentation should highlight the performance of the proposed methods against strong baselines, indicating whether the improvements are statistically significant. A discussion of both quantitative and qualitative results is essential, particularly focusing on the strengths and limitations observed. Ablation studies are crucial for understanding the impact of individual components of the proposed approach. Finally, limitations and potential future work directions should be noted to provide a balanced and insightful account of the empirical findings. The experimental results section, therefore, must demonstrate robust and reproducible evidence to support the claims of the paper, convincing the reader of the validity and impact of the research.
Future Directions#
Future research could explore several promising avenues. Extending LGD to handle diverse data modalities beyond graphs would significantly broaden its applicability. This could involve adapting the framework to handle text, images, or even multimodal data, creating a truly general-purpose foundation model. Another key direction is improving the efficiency and scalability of the model, particularly when dealing with extremely large graphs. Techniques like subgraph sampling or more efficient attention mechanisms could be investigated. Furthermore, developing more robust theoretical guarantees for LGD’s performance across different tasks and data distributions is crucial for establishing its reliability and generalizability. Finally, exploring methods for improving the interpretability and controllability of the generated graphs is vital, enabling users to better understand and influence the model’s output. This could involve techniques to explain the model’s decisions or methods for incorporating user feedback to guide the generation process.
More visual insights#
More on tables
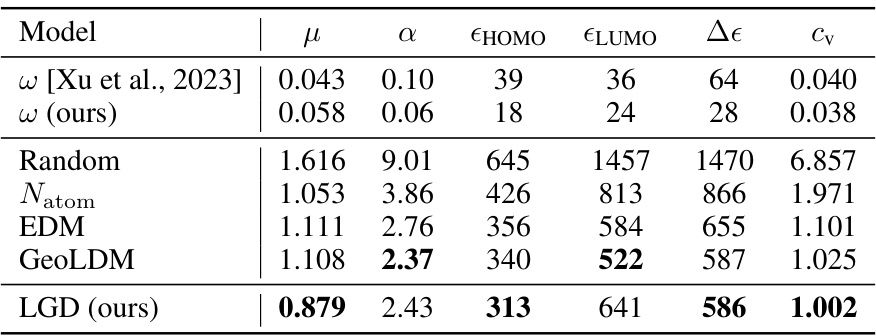
🔼 This table presents the Mean Absolute Error (MAE) results for the conditional generation task on the QM9 dataset. The MAE is a measure of the average absolute difference between the predicted and true values of six molecular properties: dipole moment (µ), polarizability (α), highest occupied molecular orbital energy (εHOMO), lowest unoccupied molecular orbital energy (εLUMO), energy gap between HOMO and LUMO (Δε), and heat capacity (cv). The table compares the performance of the proposed Latent Graph Diffusion (LGD) model against existing models (w [Xu et al., 2023], Random, Natom, EDM, GeoLDM). Lower MAE values indicate better performance.
read the caption
Table 2: Conditional generation results on QM9 (MAE ↓)
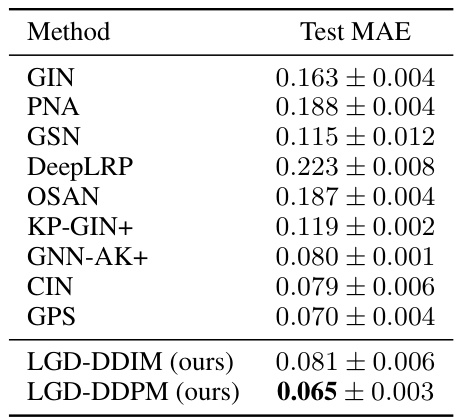
🔼 This table presents the Mean Absolute Error (MAE) results for predicting constrained solubility on the ZINC12k dataset. The MAE is a measure of regression performance, with lower values indicating better accuracy. The table compares the performance of LGD (using both DDIM and DDPM sampling methods) against several established graph-based regression models (GIN, PNA, GSN, DeepLRP, OSAN, KP-GIN+, GNN-AK+, CIN, GPS). The results show that LGD-DDPM achieves state-of-the-art performance on this task.
read the caption
Table 3: Zinc12K results (MAE ↓). Shown is the mean ± std of 5 runs.
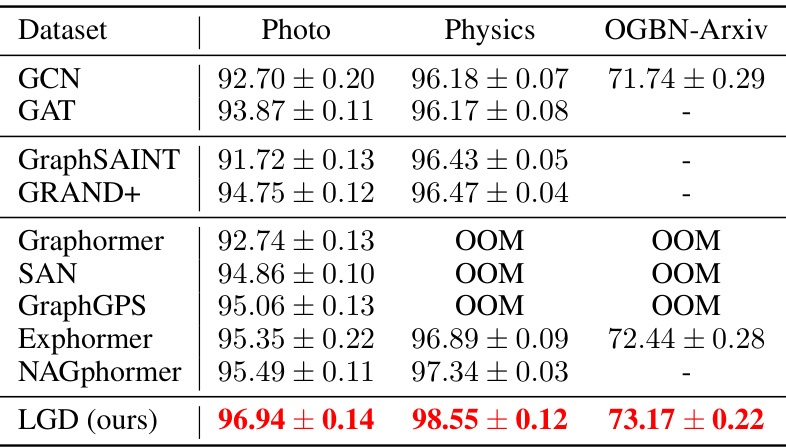
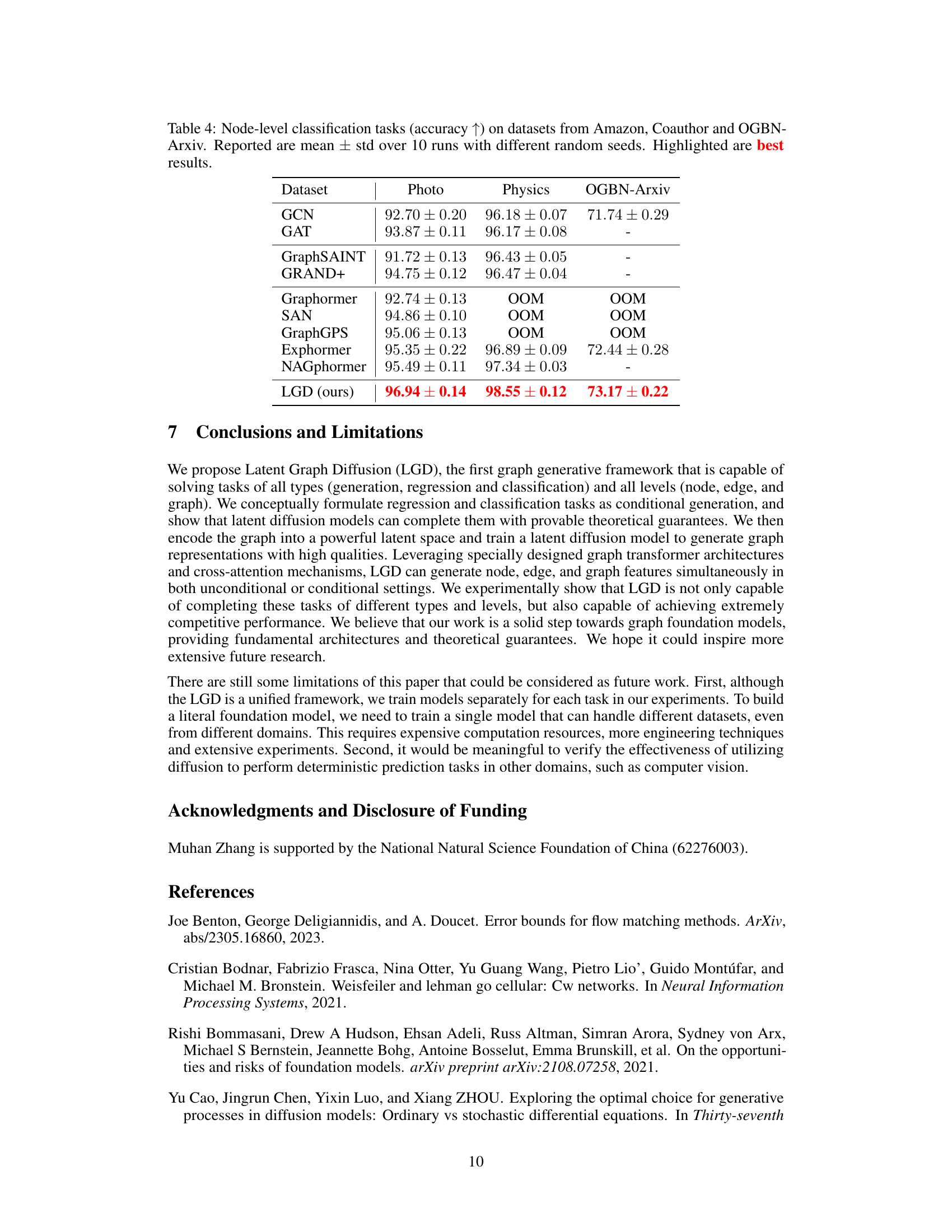
🔼 This table presents the results of node-level classification experiments conducted on three datasets: Amazon (Photo), Coauthor (Physics), and OGBN-Arxiv. Multiple models, including GCN, GAT, GraphSAINT, GRAND+, Graphormer, SAN, GraphGPS, Exphormer, and NAGphormer, were compared against the proposed LGD model. The accuracy is reported as the mean ± standard deviation over ten runs, with different random seeds used for each run. The best performance for each dataset is highlighted.
read the caption
Table 4: Node-level classification tasks (accuracy ↑) on datasets from Amazon, Coauthor and OGBN-Arxiv. Reported are mean ± std over 10 runs with different random seeds. Highlighted are best results.
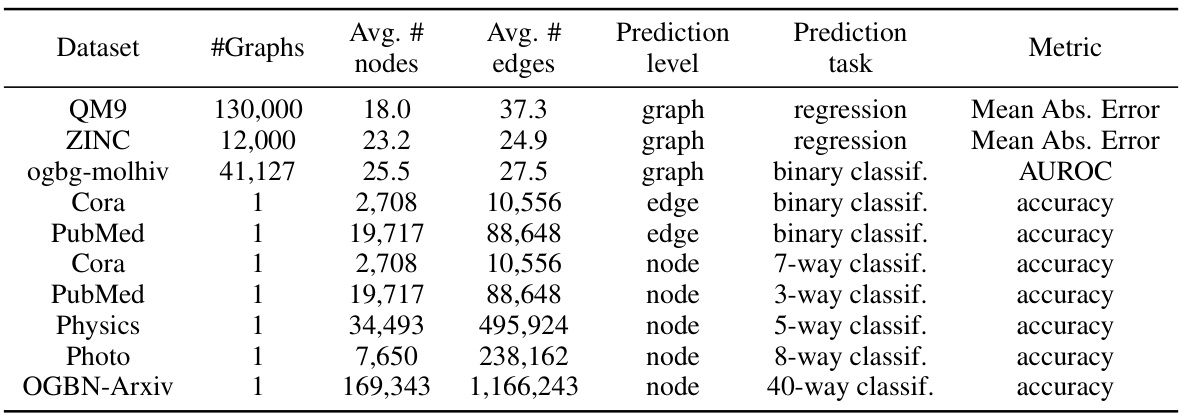
🔼 This table presents the datasets used in the paper’s experiments. For each dataset, it lists the number of graphs, the average number of nodes and edges per graph, the prediction level (node, edge, or graph), the prediction task (regression, binary classification, or multi-class classification), and the evaluation metric used (Mean Absolute Error, AUROC, or accuracy). The datasets cover various graph sizes and types of prediction tasks, demonstrating the breadth of applicability of the proposed Latent Graph Diffusion model.
read the caption
Table 5: Overview of the datasets used in the paper.

🔼 This table presents the results of large-scale molecule generation experiments on the MOSES dataset. It compares the performance of LGD against several other models, including VAE, JT-VAE, GraphINVENT, ConGress, and DiGress. The metrics used to evaluate the models include Validity (percentage of valid molecules generated), Uniqueness (percentage of unique molecules), Novelty (percentage of novel molecules not found in the training dataset), and Frechet ChemNet Distance (FCD, a measure of similarity between the generated and real molecules). The table highlights LGD’s effectiveness at one-shot generation of high-quality and novel molecules.
read the caption
Table 6: Large-scale generation on MOSES [Polykovskiy et al., 2020] dataset.
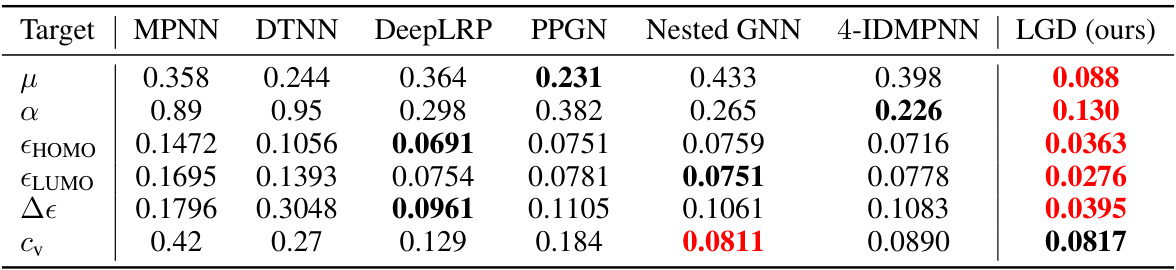
🔼 This table presents the Mean Absolute Error (MAE) for six different molecular properties predicted using various regression models on the QM9 dataset. The models compared include MPNN, DTNN, DeepLRP, PPGN, Nested GNN, 4-IDMPNN, and the authors’ proposed LGD model. Lower MAE values indicate better performance. The best and second-best results for each property are highlighted.
read the caption
Table 7: QM9 regression results (MAE ↓). Highlighted are first, second best results.
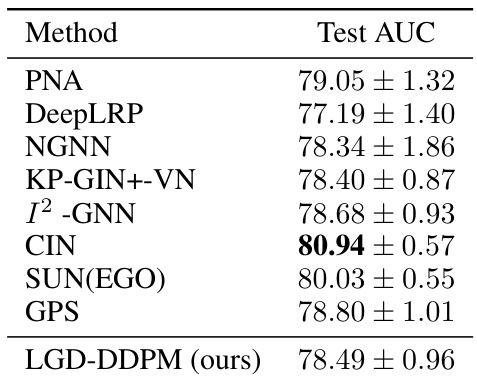
🔼 This table presents the Area Under the Curve (AUC) results for the ogbg-molhiv dataset, a graph-level classification task predicting HIV inhibition. It compares the performance of LGD-DDPM against several baseline methods, showing the mean and standard deviation of AUC scores across 5 runs. The results demonstrate the performance of LGD in comparison to existing methods on this task.
read the caption
Table 8: Ogbg-molhiv results (AUC ↑). Shown is the mean ± std of 5 runs.
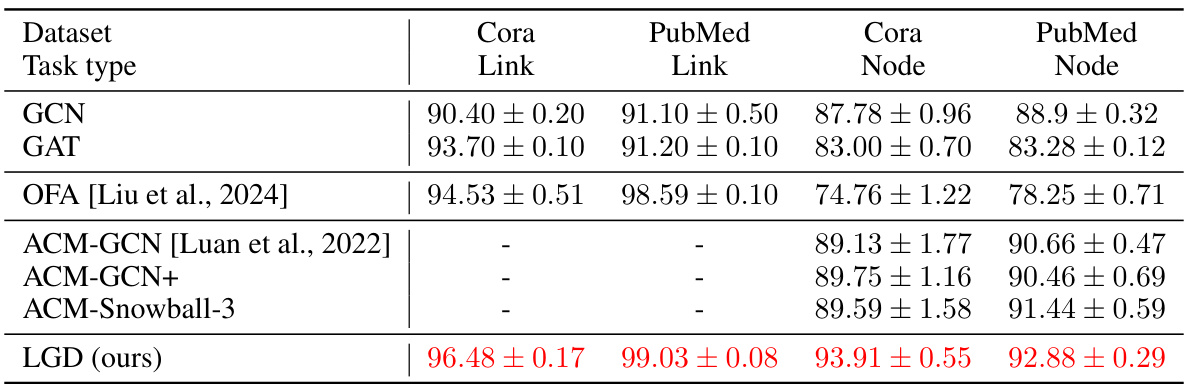
🔼 This table presents the results of node and edge classification experiments conducted on two datasets from the Planetoid benchmark: Cora and PubMed. The table compares the performance of LGD against several baseline methods (GCN, GAT, OFA, and variants of ACM-GCN) across two task types (link prediction and node classification) for each dataset. The accuracy (with standard deviation) is reported for each model and task. The best results for each setting are highlighted.
read the caption
Table 9: Node-level and edge-level classification tasks (accuracy ↑) on two datasets from Planetoid. Reported are mean ± std over 10 runs with different random seeds. Highlighted are best results.

🔼 This table presents the results of an ablation study conducted to determine the optimal latent dimension for the Latent Graph Diffusion (LGD) model on the Zinc dataset. The study varied the latent dimension (4, 8, and 16) and measured the Mean Absolute Error (MAE) for each, reporting the mean and standard deviation across three runs for each dimension. The results help determine the best balance between model capacity and performance.
read the caption
Table 10: Ablation study on latent dimension on Zinc (MAE ↓). Shown is the mean ± std of 3 runs.

🔼 This table presents the results of unconditional molecular generation experiments using the QM9 dataset. Several metrics evaluate the generated molecules, including validity (percentage of chemically valid molecules), uniqueness (percentage of unique molecules), Frechet ChemNet Distance (FCD), Neighborhood Subgraph Pairwise Distance Kernel (NSPDK), and novelty (percentage of novel molecules not found in the training set). The table compares LGD’s performance against several state-of-the-art baselines.
read the caption
Table 1: Unconditional generation results on QM9.
Full paper#