↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional regularized learning in games converges linearly to Nash equilibria, a slow process particularly challenging in online settings. This paper addresses the slow convergence issue by proposing a novel accelerated scheme, Follow The Accelerated Leader (FTXL). FTXL draws inspiration from Nesterov’s accelerated gradient algorithm and extends it to the game-theoretic setting.
The core contribution is FTXL’s ability to achieve superlinear convergence to strict Nash equilibria, significantly faster than existing methods. Crucially, this speedup holds true even under various information limitations, ranging from full information to bandit feedback where players only observe their own immediate payoffs, thus enhancing the algorithm’s practical relevance to a wider array of real-world game scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it bridges the gap between convex optimization and game theory, offering a novel accelerated learning algorithm (FTXL) with superior convergence rates for finding Nash equilibria. Its applicability across various feedback structures (full information, realization-based, and bandit) makes it highly relevant to diverse online learning scenarios in games. The findings open new avenues for research into faster and more robust learning algorithms in multi-agent systems.
Visual Insights#
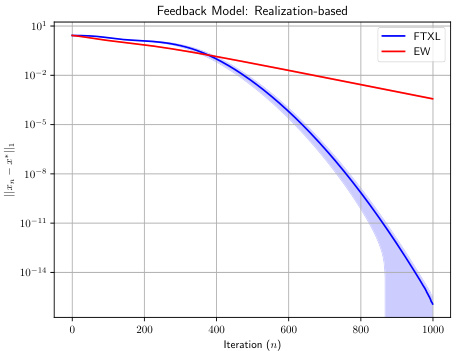
This figure compares the performance of the FTXL algorithm against the standard EW algorithm across four scenarios. The scenarios are divided by game type (zero-sum and congestion) and feedback type (realization-based and bandit). The plots show the average distance from equilibrium over many runs, with shaded regions indicating the standard deviation. The logarithmic scale emphasizes the algorithms’ convergence rates.
In-depth insights#
FTXL: Accelerated Learning#
The heading ‘FTXL: Accelerated Learning’ suggests a novel approach to online learning in game theory. FTXL (Follow the Accelerated Leader) likely modifies existing regularized learning methods like FTRL (Follow the Regularized Leader), by incorporating momentum, inspired by Nesterov’s accelerated gradient algorithm. This acceleration aims to drastically improve convergence rates to Nash equilibria, potentially achieving a superlinear rate compared to FTRL’s geometric convergence. The core idea is to add an inertial term, mimicking the ‘heavy ball with vanishing friction’ interpretation of Nesterov’s method, enabling players to ‘build momentum’ towards equilibrium. The paper likely demonstrates this accelerated convergence in various information settings, from full-information to bandit feedback, showcasing its robustness. A key insight is that even with limited information, the algorithm maintains its superlinear rate, highlighting its potential applicability in realistic scenarios where players have imperfect knowledge. The approach combines the power of accelerated optimization and regularized learning in games, offering a significant step towards more efficient and robust learning dynamics.
Superlinear Convergence#
The concept of “superlinear convergence” in the context of this research paper centers on the remarkably fast rate at which the proposed accelerated learning algorithms converge to a solution (Nash equilibrium). Unlike traditional methods exhibiting linear convergence (geometric decay), superlinear convergence implies an increasingly rapid approach to the equilibrium as the algorithm progresses, achieving an exponential speed-up. This accelerated convergence is particularly significant in game-theoretic settings, where finding equilibria can be computationally challenging. The paper’s achievement lies in demonstrating superlinear convergence across different levels of information feedback, including full information, realization-based, and even bandit feedback scenarios. This robustness is a crucial contribution, as it shows the algorithm’s effectiveness even when players’ knowledge is limited. The theoretical analysis, supported by numerical experiments, firmly establishes the superlinear convergence rate and underscores the practical advantages of this accelerated learning approach in a variety of game-theoretic contexts.
Info Feedback Robustness#
Info Feedback Robustness examines how well learning algorithms perform under different information conditions. The core idea is to assess the algorithm’s resilience when the information available to the players is incomplete, noisy, or delayed. A robust algorithm should maintain its performance regardless of the feedback structure, whether it is full information, realization-based feedback (observing outcomes of unchosen actions), or bandit feedback (only observing the immediate payoff of the selected action). The analysis would likely involve evaluating convergence rates, equilibrium selection, and overall accuracy across varied feedback scenarios. Key factors determining robustness include regularization techniques, exploration strategies, and the algorithm’s inherent stability. Algorithms demonstrating high robustness are crucial for real-world applications where perfect information is seldom available, offering a significant advantage in complex environments. The theoretical analysis might also include bounds on performance degradation under imperfect information, and experimental validation across diverse game types and feedback structures would complement theoretical findings. Ultimately, understanding info feedback robustness is key to building reliable and effective learning agents that can thrive in unpredictable situations.
NAG Game-Theoretic Use#
The application of Nesterov’s Accelerated Gradient (NAG) algorithm, a cornerstone of convex optimization, to game theory presents a compelling challenge. Extending NAG’s success in minimizing convex functions to the inherently non-convex landscape of finding Nash equilibria in games requires careful consideration. The core idea revolves around adapting NAG’s momentum mechanism within the framework of regularized learning, leading to the proposed ‘Follow the Accelerated Leader’ (FTXL) algorithms. The key insight is that NAG’s continuous-time equivalent offers a pathway to accelerate the convergence of regularized learning methods in games. However, translating this continuous-time intuition to practical, discrete-time algorithms suitable for various information feedback structures (full-information, realization-based, bandit) poses significant challenges. The authors demonstrate that despite these complexities, FTXL algorithms maintain superlinear convergence to strict Nash equilibria, offering a substantial speedup over traditional methods. A crucial aspect is handling the algorithm’s dependence on initial conditions and properly managing feedback information. Furthermore, the analysis explores how these aspects affect convergence rates. The exploration of various information feedback scenarios highlights FTXL’s robustness, and the theoretical analysis, supported by numerical experiments, provides strong evidence of the algorithm’s efficacy and accelerated performance.
Future Research: Bandits#
Future research into bandit algorithms within the context of accelerated regularized learning in games holds significant promise. A key area would be developing more sophisticated bandit algorithms that can handle the complexities of game-theoretic settings, such as those with partial or delayed feedback. Investigating how different exploration strategies impact convergence rates and equilibrium selection would be critical. Another avenue is exploring adaptive learning rates and regularizers that can automatically adjust to the game’s dynamics and information structure. This is important because the performance of accelerated methods is often sensitive to these parameters. Furthermore, theoretical analysis is needed to provide stronger convergence guarantees and understand the interplay between acceleration, regularization, and the bandit feedback mechanism. Finally, applying these advanced bandit-based accelerated learning algorithms to real-world scenarios would be particularly insightful, such as in online advertising, auction design, or multi-agent reinforcement learning problems. This would provide a practical test of the theoretical advancements and uncover new challenges and opportunities.
More visual insights#
More on figures

This figure compares the performance of the proposed FTXL algorithm against the standard EW algorithm in two different game scenarios: a zero-sum game and a congestion game. Both algorithms are tested under two feedback conditions: realization-based feedback and bandit feedback. The plots show the average distance between the algorithm’s strategy and a strict Nash equilibrium over multiple iterations. Shaded areas represent the standard deviation, illustrating the variability of the results. The y-axis uses a logarithmic scale to highlight differences in convergence rates.

This figure compares the performance of the proposed FTXL algorithm against the standard EW algorithm in two different game settings: a zero-sum game and a congestion game. The comparison is done under two different feedback mechanisms: realization-based feedback and bandit feedback. The plots show the average distance from the equilibrium over multiple runs for each algorithm and feedback type, with shaded regions illustrating the standard deviation. The logarithmic scale highlights the convergence rates. FTXL consistently demonstrates superior performance.

The figure displays the performance of the FTXL algorithm in two different games (zero-sum and congestion) under two different feedback mechanisms (realization-based and bandit). The plots show the average distance from the equilibrium over 1000 iterations, comparing FTXL to a standard EW algorithm. Shaded regions represent the standard deviation for each algorithm. The y-axis is logarithmic, emphasizing the rate of convergence.
Full paper#