TL;DR#
Current PAC-Bayes bounds are limited to scalar metrics like error rate, failing to capture the complexities of real-world problems where different errors have varying severities. This restricts the ability to provide information-rich certificates for the complete performance, especially in scenarios like medical diagnosis where Type I and Type II errors have different significances. This makes it harder to obtain tight bounds on any specific weighting of these errors.
This paper introduces a novel PAC-Bayes bound to address this issue. It simultaneously controls the probabilities of an arbitrary finite number of user-specified error types, providing a richer, more informative generalization guarantee. The bound is transformed into a differentiable training objective, enabling direct optimization within neural network training. This approach addresses the limitations of existing methods by implicitly controlling all possible linear combinations of the errors simultaneously, improving the robustness and reliability of the model’s performance in more complex applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generalization bounds and machine learning theory. It offers a novel framework for analyzing and controlling multiple error types simultaneously, which is particularly relevant for complex real-world scenarios where different errors may have varying severities. This work could lead to the development of more robust and reliable machine learning models, and opens up new avenues for investigation in PAC-Bayes theory.
Visual Insights#

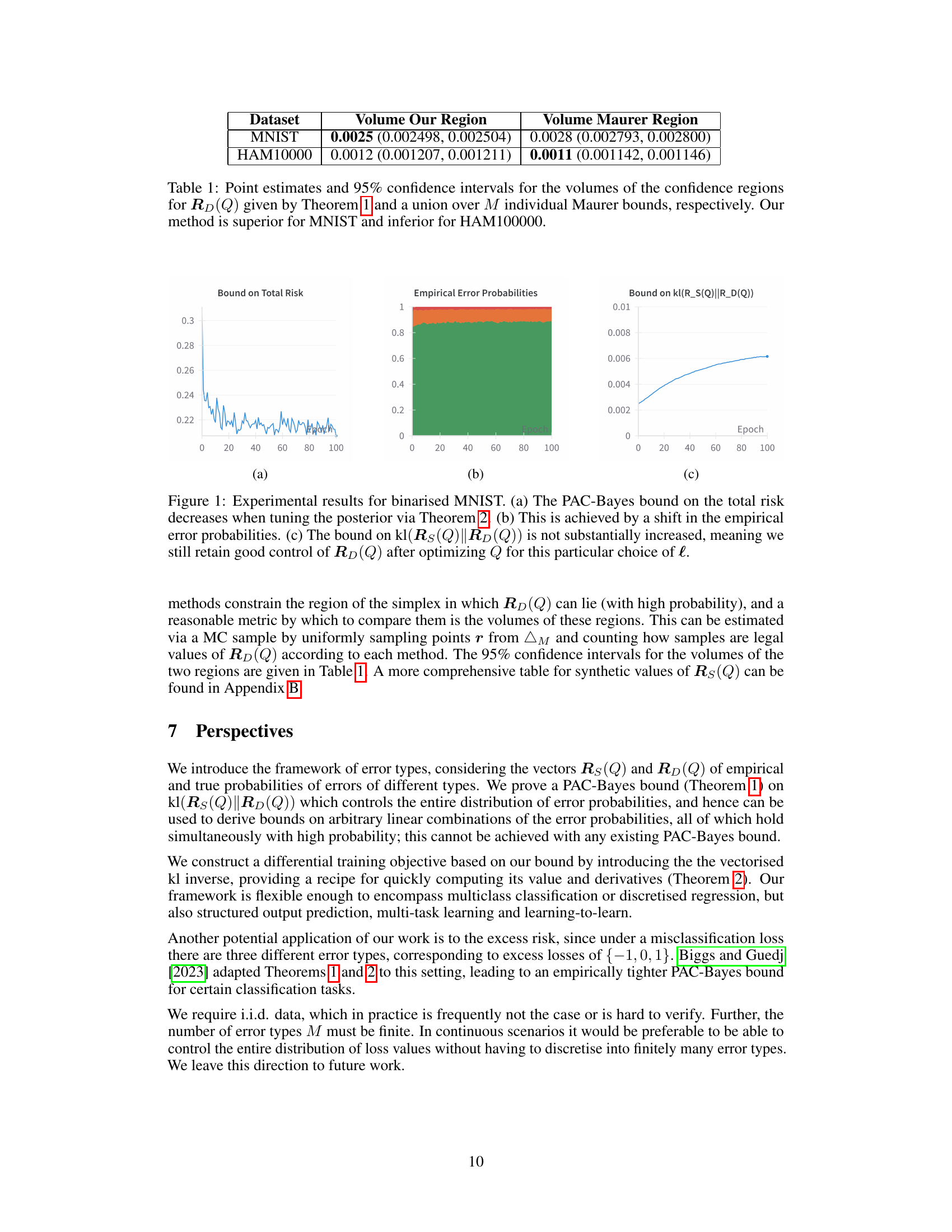
🔼 This figure shows experimental results for the binarised MNIST dataset. Subfigure (a) displays the decrease in the PAC-Bayes bound on the total risk as the posterior is tuned using Theorem 2. Subfigure (b) illustrates the corresponding shift in the empirical error probabilities. Finally, subfigure (c) demonstrates that the bound on the KL-divergence between the empirical and true risk vectors does not increase significantly, indicating that good control of the true risk is maintained despite optimizing for a specific loss vector.
read the caption
Figure 1: Experimental results for binarised MNIST. (a) The PAC-Bayes bound on the total risk decreases when tuning the posterior via Theorem 2. (b) This is achieved by a shift in the empirical error probabilities. (c) The bound on kl(Rs(Q)||RD(Q)) is not substantially increased, meaning we still retain good control of RD(Q) after optimizing Q for this particular choice of l.

🔼 This table presents a comparison of the volume of confidence regions for the true risk vector RD(Q), obtained using two different methods: the authors’ proposed method (Theorem 1) and a method based on a union of Maurer bounds. The volume represents the size of the region in the probability simplex where RD(Q) is likely to fall. Smaller volumes indicate tighter bounds. The results show that for the MNIST dataset, the authors’ method yields a smaller confidence region, indicating tighter bounds, while for the HAM10000 dataset, the Maurer bound produces a smaller region.
read the caption
Table 1: Point estimates and 95% confidence intervals for the volumes of the confidence regions for RD(Q) given by Theorem 1 and a union over M individual Maurer bounds, respectively. Our method is superior for MNIST and inferior for HAM10000.
Full paper#