↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for understanding neural activity struggle to balance modeling complexity and interpretability. Highly expressive nonlinear models are hard to interpret, while simpler linear models lack the capacity to capture complex dynamics. This creates a need for methods that can capture the nuances of neural activity without sacrificing interpretability. Recurrent switching linear dynamical systems (rSLDS) offer a compromise but suffer from artifacts such as oscillations near state boundaries and a lack of uncertainty estimates.
This paper introduces the Gaussian Process Switching Linear Dynamical System (gpSLDS), a new model which addresses these issues. gpSLDS uses a Gaussian process (GP) to model the nonlinear dynamics, but incorporates a novel kernel function that ensures smoothly interpolated locally linear dynamics, similar to rSLDS. This approach retains interpretability while allowing for flexible and smooth dynamics. The model is fit using a modified learning objective that improves the estimation accuracy. Results on synthetic and real neural data show that gpSLDS outperforms rSLDS and other state-of-the-art models.
Key Takeaways#
Why does it matter?#
This paper is crucial for neuroscientists and machine learning researchers. It introduces a novel and flexible model (gpSLDS) for analyzing neural data, bridging the gap between expressive nonlinear models and interpretable linear ones. This will improve the accuracy and interpretability of neural dynamics analyses, leading to deeper insights into brain function and potentially impacting various applications of dynamic system models.
Visual Insights#
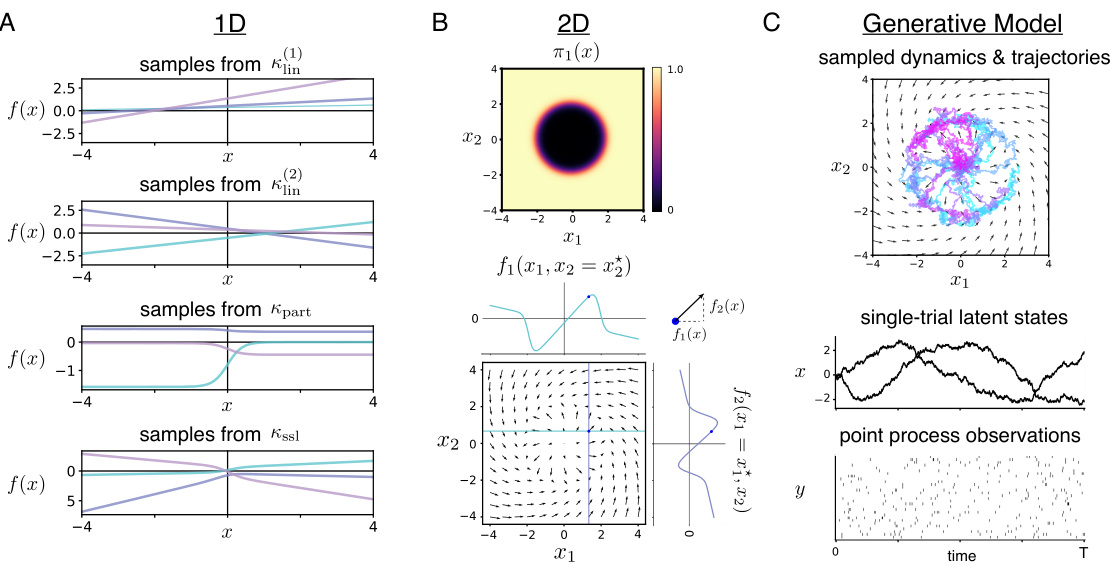
This figure illustrates the Smoothly Switching Linear (SSL) kernel, a core innovation of the paper. Panel A shows 1D function samples from different kernels to highlight the properties of the SSL kernel. Panel B demonstrates a 2D example of π(x) and resulting dynamics. Panel C provides a schematic overview of the generative model, showing how simulated trajectories are generated based on the sampled dynamics and observed via Poisson process or Gaussian observations.
In-depth insights#
gpSLDS: A New Model#
The proposed gpSLDS model offers a novel approach to modeling latent neural dynamics by combining the strengths of Gaussian Process Stochastic Differential Equations (GP-SDEs) and recurrent switching linear dynamical systems (rSLDS). Unlike traditional GP-SDEs that can lead to complex and less interpretable dynamics, gpSLDS leverages a novel kernel function that enforces smoothly interpolated, locally linear dynamics, thereby improving interpretability. This approach effectively addresses the limitations of rSLDS, such as artificial oscillations near state boundaries and a lack of posterior uncertainty estimates. The key innovation lies in the smoothly switching linear (SSL) kernel, which allows for flexible yet interpretable dynamics akin to rSLDS but with the added benefits of posterior uncertainty. This is achieved through posterior uncertainty estimation and a modified learning objective, improving kernel hyperparameter estimation accuracy. The gpSLDS presents a powerful tool that balances expressiveness with interpretability, offering a significant improvement over existing methods for modeling neural population activity. The method’s application to both synthetic and real neuroscience data demonstrated superior performance in comparison to existing models.
Nonlinear Dynamics#
The concept of nonlinear dynamics in neural systems is crucial because neural activity rarely follows simple linear patterns. Instead, complex interactions between neurons often lead to intricate, non-additive behaviors. Understanding these nonlinear dynamics is vital for interpreting neural computations and behavior, as linear models often fall short of capturing the richness and complexity of neural responses. The challenge lies in balancing the need for expressive models capable of handling nonlinearity with the desire for interpretability—a trade-off that many researchers grapple with. Advanced techniques, such as Gaussian processes or recurrent switching linear dynamical systems, are employed to capture the nonlinear aspects of neural activity while still maintaining some level of analytical tractability. This involves careful consideration of the model’s architecture and the prior knowledge incorporated to ensure both flexibility and interpretability in the resulting model fits. Ultimately, the goal is to develop models that accurately reflect the complexities of the system while offering valuable insights into how the neural system achieves its computations. Addressing the challenges posed by nonlinear dynamics is crucial for a comprehensive understanding of the brain’s functional mechanisms.
Interpretable Dynamics#
The concept of “Interpretable Dynamics” in the context of neural population activity analysis centers on the challenge of balancing model expressiveness with the ability to understand the underlying mechanisms. High-dimensional neural data often requires complex, nonlinear models to capture its nuances. However, such complexity often sacrifices interpretability, making it difficult to extract meaningful biological insights. The ideal approach would generate models that are both capable of capturing intricate dynamics and easily understandable in terms of the neural system’s functional components. This requires developing methods that can uncover low-dimensional representations of high-dimensional data while maintaining a clear connection between the model’s parameters and the biological processes involved. The inherent trade-off between model accuracy and human interpretability is a major challenge in this field. Successfully addressing this issue would unlock a deeper understanding of neural computation, behavior, and disease.
Neural Data Analysis#
Analyzing neural data presents unique challenges due to its high dimensionality, noise, and complexity. Effective analysis requires sophisticated statistical and computational methods to extract meaningful information. Common techniques include dimensionality reduction, such as principal component analysis (PCA) or t-SNE, to visualize and interpret the data. Modeling neural activity using dynamical systems provides a powerful framework, allowing researchers to capture the temporal evolution of neural states and investigate underlying computational mechanisms. Gaussian processes (GPs) offer a flexible and nonparametric approach to model nonlinear dynamics, but inference can be computationally intensive. Combining GPs with switching linear dynamical systems (SLDS) models offers a balance between expressiveness and interpretability, enabling flexible modeling while maintaining a degree of structure. Developing methods to handle noisy and irregularly sampled data remains crucial, as does the need for robust statistical inference techniques to quantify uncertainty and avoid overfitting.
Future Research#
Future research directions stemming from this Gaussian Process Switching Linear Dynamical System (gpSLDS) model are multifaceted. Improving computational efficiency is paramount, especially for high-dimensional latent spaces. Exploring alternative inference methods beyond variational approaches, such as Markov Chain Monte Carlo (MCMC), could yield more accurate posterior estimates, but at a potentially higher computational cost. The development of more sophisticated kernel functions that capture more complex nonlinear relationships while maintaining interpretability is another critical avenue. Investigating the impact of different feature transformations on the smoothly switching linear kernel could further enhance model flexibility. Finally, extending the model to handle diverse neural data modalities (e.g., EEG, ECoG) and incorporating additional biological constraints would significantly broaden the gpSLDS applicability and enhance its biological interpretability. The systematic study of how different hyperparameters influence model performance and how best to tune them for optimal results in various datasets warrants dedicated investigation. Ultimately, rigorous benchmarking against existing methods across various neural datasets is crucial to fully establish the gpSLDS as a robust and reliable tool for neuroscience research.
More visual insights#
More on figures
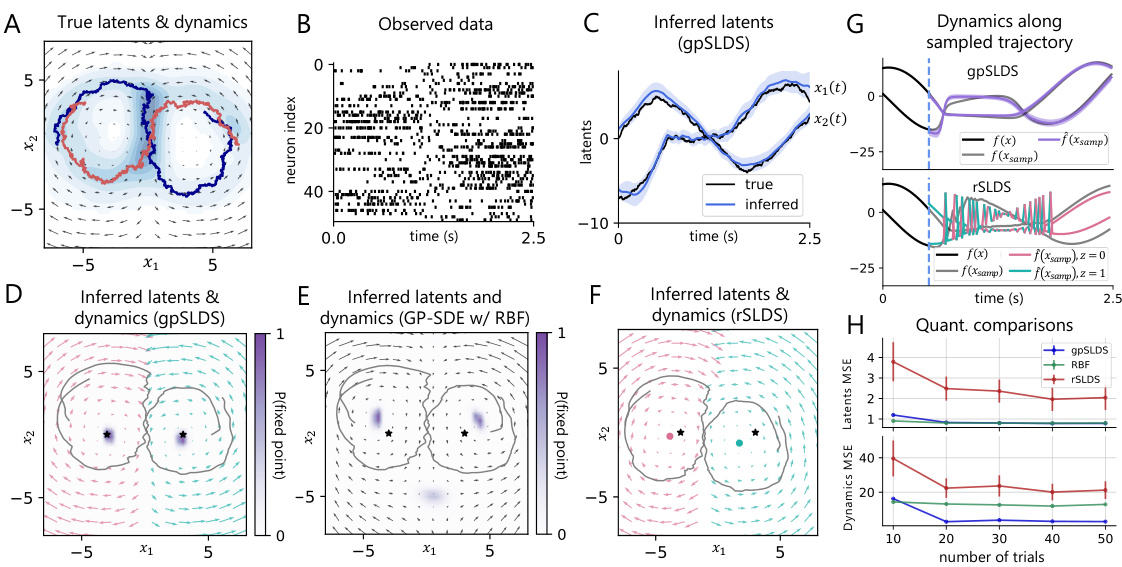
The figure displays the results of applying the gpSLDS, rSLDS, and GP-SDE with RBF kernel to a synthetic dataset of two linear rotational systems. Panels A-F visually compare the true and inferred latent states and dynamics, highlighting the gpSLDS’s ability to accurately recover the true dynamics and identify fixed points. Panel G illustrates the differences in how uncertainty is expressed by the gpSLDS and rSLDS. Finally, Panel H provides a quantitative comparison of the three models in terms of mean squared error (MSE) for both latent states and dynamics, demonstrating the gpSLDS’s superior performance.
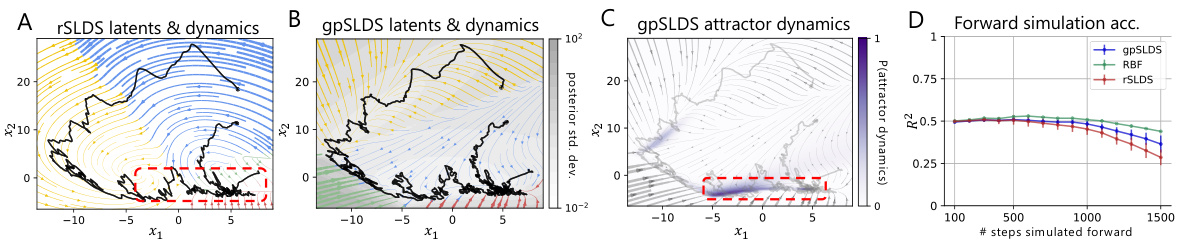
This figure compares the results of applying rSLDS, gpSLDS, and GP-SDE with RBF kernel to real neural data from Nair et al. [27] concerning hypothalamic activity during aggression. Panels A-C visualize the latent dynamics inferred by the rSLDS and gpSLDS models, highlighting the identification of a line attractor by the gpSLDS with associated uncertainty estimates. Panel D shows a quantitative comparison of the in-sample forward simulation accuracy across the models, demonstrating the gpSLDS’s improved performance compared to rSLDS.

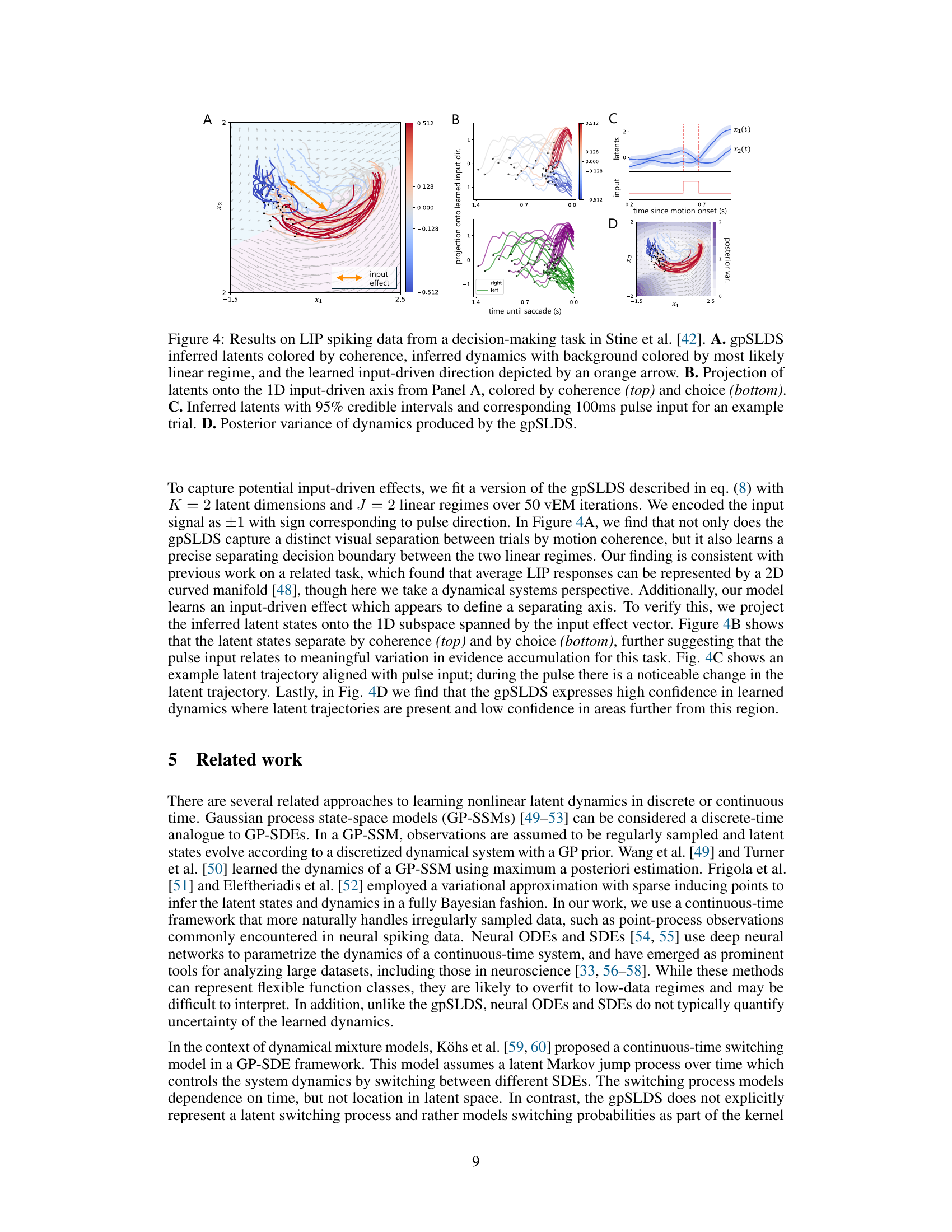
This figure shows the results of applying the gpSLDS model to LIP spiking data from a decision-making task. Panel A shows the inferred latent states colored by coherence, the inferred dynamics with background colored by the most likely linear regime, and the learned input-driven direction. Panel B shows the projection of latents onto the 1D input-driven axis, colored by coherence and choice. Panel C shows the inferred latents with 95% credible intervals and the corresponding 100ms pulse input for an example trial. Panel D shows the posterior variance of dynamics produced by the gpSLDS model.
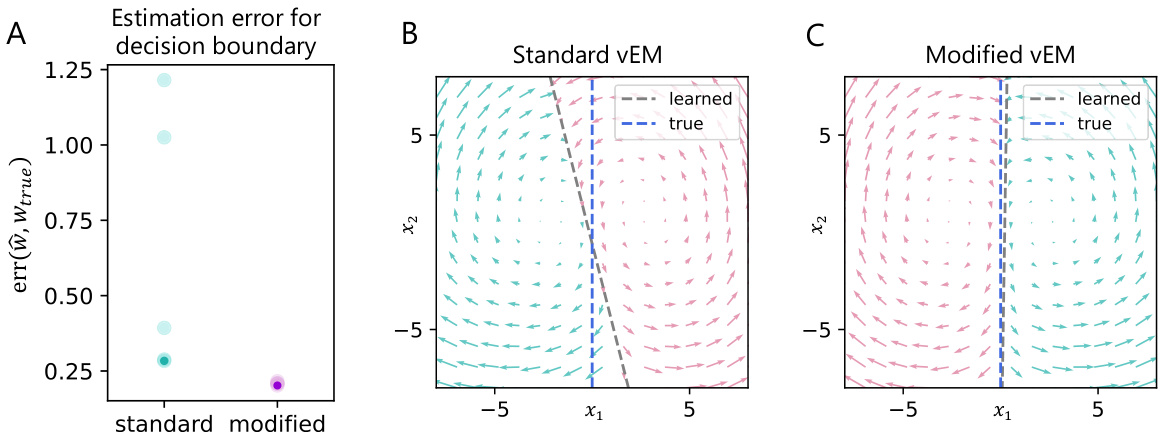
This figure compares the performance of standard and modified variational expectation-maximization (vEM) approaches for learning the hyperparameters of Gaussian Process Switching Linear Dynamical Systems (gpSLDS). Panel A shows the error in estimating the decision boundary between two dynamical regimes for five model fits using each vEM method. Panel B displays the learned and true decision boundaries for the standard vEM, illustrating failure to learn the true boundary. Panel C shows that the modified vEM successfully learns the true boundary.
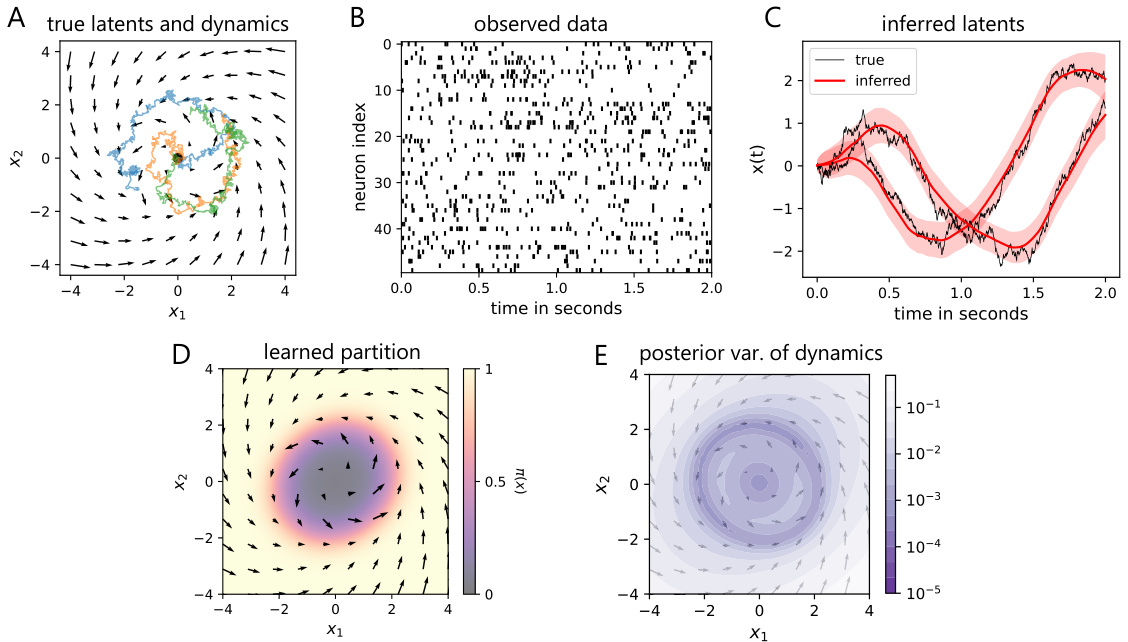
This figure displays the results of applying the gpSLDS model to a synthetic dataset with a 2D limit cycle. The true dynamics consist of an unstable and a stable rotation around (0,0), separated by a nonlinear boundary (x1 + x2 = 4). The gpSLDS successfully infers the latent trajectories, accurately recovers the nonlinear boundary, and appropriately reflects uncertainty in its dynamics estimates (low variance in high-density regions, high variance elsewhere). The figure demonstrates the model’s ability to handle nonlinear decision boundaries.
Full paper#