↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
In-context learning (ICL), where language models solve tasks using only a few examples within the input prompt, has emerged as a powerful mechanism in large language models. However, our understanding of ICL’s optimization and generalization properties remains limited, particularly concerning the influence of architectural choices, low-rank parameterizations, and data correlations. Existing studies often make simplifying assumptions about the data and model parameters.
This paper rigorously analyzes ICL in linear Transformers and a state-space model (H3), demonstrating that both models implement a single step of preconditioned gradient descent under suitable conditions. The work introduces correlated data designs, proving how distributional alignment improves sample complexity. Further, the study derives optimal low-rank solutions for attention weights, providing insights into LoRA adaptation. The results are validated through extensive empirical experiments, offering a comprehensive understanding of ICL’s mechanics.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly advances our understanding of in-context learning (ICL), a critical mechanism in large language models. By providing a more thorough theoretical framework and addressing practical limitations, the research opens new avenues for improving ICL efficiency and robustness, impacting various applications in NLP and beyond. The insights provided are directly relevant to ongoing efforts to optimize LLM performance and better understand their capabilities.
Visual Insights#
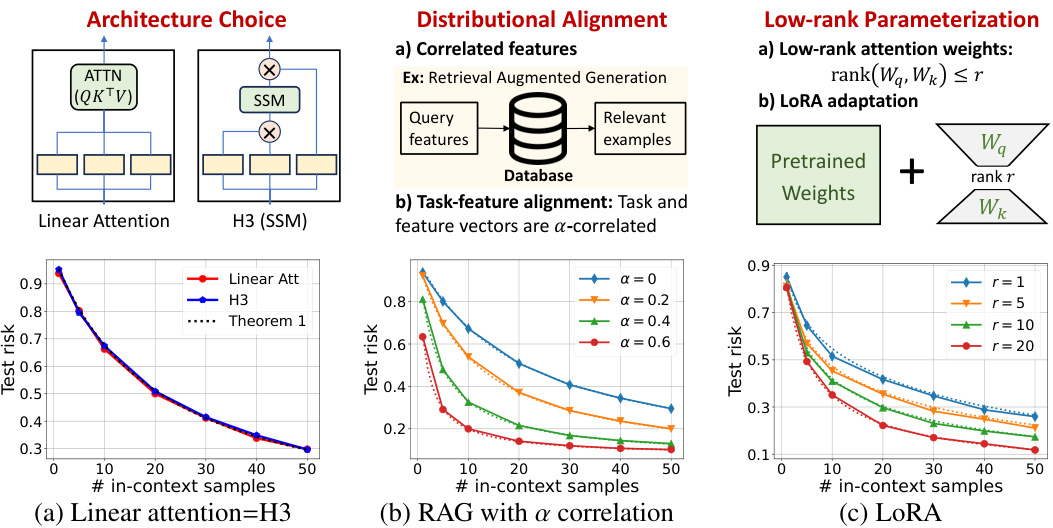
This figure shows the empirical and theoretical results of the in-context learning optimization landscape. It explores three key aspects: 1. Architecture Choice: Compares the performance of linear attention and H3 (a state-space model) in ICL. 2. Distributional Alignment: Investigates how correlated features (Retrieval Augmented Generation - RAG and task-feature alignment) affect ICL sample complexity. 3. Low-rank Parameterization: Analyzes the optimal risk with low-rank attention weights and how LoRA adapts to new distributions. Solid lines represent empirical performance, while dotted lines represent theoretical predictions from Section 3.
In-depth insights#
ICL Optimization#
In the context of in-context learning (ICL), optimization strategies are crucial for effective performance. The paper likely explores how gradient-based methods, such as preconditioned gradient descent (PGD), are implicitly implemented by models like linear attention and H3. A core aspect of ICL optimization may involve understanding how these models adapt to various data distributions, including scenarios with correlated features or distributional alignment. Low-rank parameterization techniques, such as LoRA, are also likely explored as means for efficient adaptation to new tasks or distributions. The effectiveness of these methods is likely assessed through theoretical risk bounds and empirical evaluations, providing insights into sample complexity and generalization performance. The optimization landscape may be analyzed under assumptions of data independence or correlation, revealing how these factors impact the efficiency and convergence of ICL. Distributional alignment might be identified as a key factor in improving sample efficiency, highlighting the significance of task-feature relationships. Ultimately, the paper likely aims to provide a deeper understanding of the optimization mechanics of ICL and how various architectural choices and parameterizations influence its success.
Low-rank ICL#
Low-rank In-Context Learning (ICL) explores the efficiency of ICL when model parameters, specifically attention weights, are constrained to low-rank matrices. This approach reduces the number of parameters significantly, leading to faster training and inference, and potentially improved generalization. The core idea is that in many ICL tasks, only a small subspace of the feature space is relevant, and thus low-rank representations are sufficient to capture the essential information. Low-rank parameterization, such as LoRA (Low-Rank Adaptation), allows for adapting pre-trained models to new tasks with minimal parameter updates. This is particularly beneficial for large language models where full fine-tuning is computationally expensive. Analyzing the optimization and risk landscape of low-rank ICL requires understanding how the reduced parameter space impacts the learning dynamics and generalization performance. Theoretical analysis is crucial to understanding the optimal rank, the effect of data distribution on the low-rank approximation, and the overall efficacy of low-rank ICL. Empirical evaluations further demonstrate that low-rank ICL can indeed achieve comparable performance to full-rank models while significantly reducing computational costs.
H3 vs. Attention#
The comparison of H3 and linear attention mechanisms within the context of in-context learning (ICL) reveals intriguing similarities and differences. Both models, under specific correlated design assumptions, demonstrably implement a single-step gradient descent (PGD) optimization, effectively converging to the optimal solution in one step. However, H3 exhibits a key advantage through its inherent gating mechanism, which acts as a sample weighting mechanism. This feature allows H3 to outperform linear attention, particularly in scenarios involving temporal heterogeneity. The theoretical analysis highlights how the H3 architecture, thanks to its convolutional filters, naturally incorporates sample weighting and distributional alignment. This detailed analysis provides insights into sample complexity and the role of data correlation in enhancing ICL performance. In essence, while both models achieve similar results under simplified conditions, the architectural advantages of H3 grant it superior performance in real-world settings characterized by complex data relationships.
Distributional Effects#
Distributional effects in machine learning, particularly within the context of in-context learning (ICL), explore how the statistical properties of the data significantly impact model performance and generalization. Data characteristics, like correlation between task and feature vectors, or the presence of distributional shifts between training and testing sets, are crucial. The paper investigates the effects of correlated designs in ICL, showing how distributional alignment between training and test samples boosts sample efficiency. Retrieval Augmented Generation (RAG) is analyzed as an example, revealing its dependence on distributional alignment. The impact of low-rank parameterizations, such as LoRA, on adapting models to new distributions is also a significant aspect. The theoretical results are reinforced by empirical experiments, validating the importance of considering the distributional nuances of the data for effective ICL. Overall, understanding and leveraging distributional effects is crucial for designing robust and efficient ICL systems.
Future of ICL#
The future of in-context learning (ICL) is ripe with exciting possibilities. A deeper theoretical understanding of ICL’s mechanisms, moving beyond current linear models to encompass richer architectures and non-linear dynamics, is crucial. This includes investigating how ICL interacts with various forms of distributional shift and developing robust methods for adaptation. Advances in low-rank parameterization and efficient optimization techniques will be key to scaling ICL to larger models and datasets while mitigating computational costs. Bridging the gap between theoretical understanding and practical applications is paramount. This requires exploring the use of ICL in complex real-world settings and evaluating its performance on diverse tasks involving noisy or ambiguous data. Furthermore, exploring the interplay between ICL and other learning paradigms such as transfer learning and meta-learning promises to unlock new capabilities. Finally, careful consideration of potential risks and societal implications is needed to ensure responsible development and deployment of ICL-based systems.
More visual insights#
More on figures
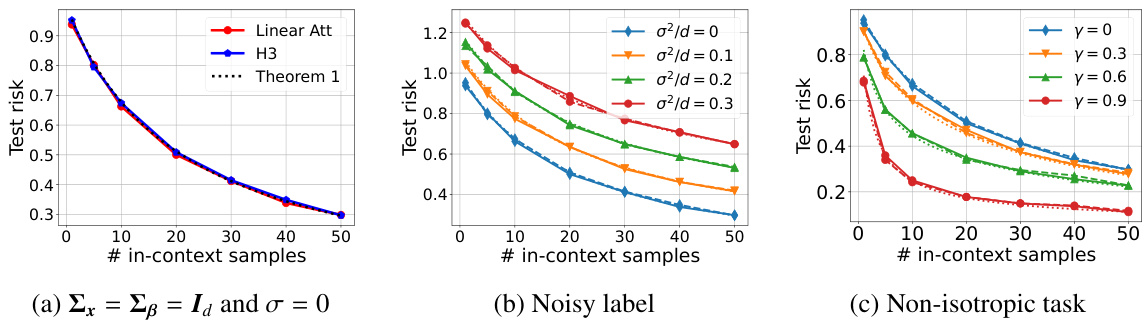
This figure empirically validates Theorem 1 and Proposition 1 of the paper by comparing the performance of linear attention and H3 models on three different scenarios: noiseless i.i.d data, noisy labels, and non-isotropic task data. The results show a strong agreement between the empirical performance and theoretical predictions, supporting the equivalence between the two models and their implementation of gradient descent.
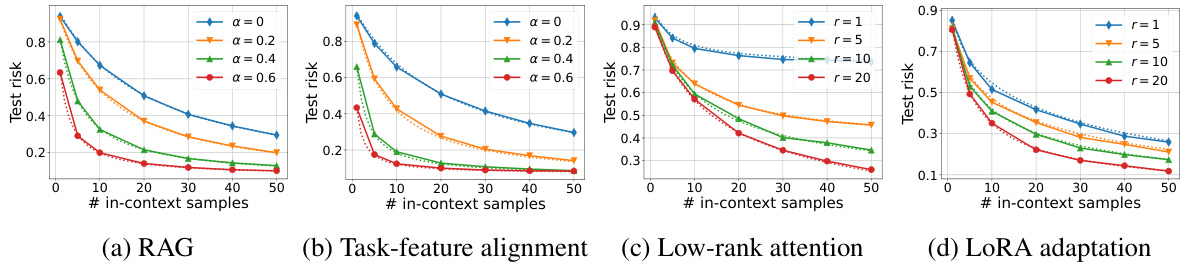
This figure displays experimental results related to distributional alignment (RAG and task-feature alignment) and low-rank parameterization in in-context learning. It shows how performance changes with varying levels of alignment (parameter α) and rank reduction (parameter r). The graphs compare empirical results (solid lines) with theoretical predictions (dotted lines), demonstrating the alignment between theory and experiments.
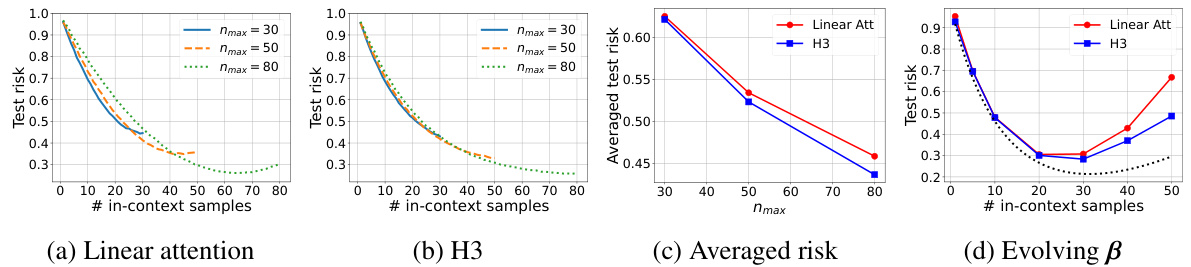
This figure empirically validates Theorem 1 and Proposition 1 of the paper. It shows the results of training 1-layer linear attention and H3 models on linear regression tasks with various conditions. The plots compare the empirical test risk (solid lines) with the theoretical predictions from the theorems (dotted lines). Panel (a) shows the noiseless IID data case, (b) demonstrates the impact of noisy labels, and (c) examines non-isotropic tasks (i.e. the case where the task covariance matrix is not an identity matrix). The close agreement between empirical results and theoretical predictions confirms the theoretical findings.
Full paper#



















