↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many anomaly detection systems lack interpretability, hindering trust and reliable usage. Current methods often focus on locating anomalies, but not on explaining why they are anomalies. This paper introduces AR-Pro, a framework for generating counterfactual explanations in the form of anomaly repairs. It tackles this by formally specifying what a non-anomalous version should look like.
AR-Pro introduces a domain-independent framework for generating and evaluating counterfactual explanations for anomaly detection. It leverages the linear decomposability property of many anomaly detectors and uses it to define domain-independent properties for high-quality anomaly repairs. Generative models, specifically diffusion models, are used to produce these repairs, guided by the defined properties. The paper demonstrates AR-Pro’s effectiveness on various datasets, showcasing superior performance compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical issue of explainability in anomaly detection, a problem that limits the reliability and trustworthiness of many current methods. It proposes a novel framework, AR-Pro, that enhances the understanding of anomaly detection models by providing counterfactual explanations. This will lead to increased confidence in their predictions and allow experts and non-experts alike to better interpret the results. AR-Pro’s domain-independent framework offers a new avenue for research into explainable AI, potentially improving the adoption and usage of anomaly detection across various fields.
Visual Insights#

This figure illustrates the AR-Pro framework for generating counterfactual explanations of anomalies. It begins by using an anomaly detector to identify anomalous regions within an input (image or time series). Then, it uses property-guided diffusion to repair these regions, generating a counterfactual example of what a non-anomalous version should look like. The quality of this repair is evaluated based on four properties: Overall Improvement (lower anomaly score), Similarity (resemblance to the original), Localized Improvement (improved score in the repaired region), and Non-degradation (no significant worsening of the score in the non-anomalous regions).

This table presents a quantitative comparison of the performance of AR-Pro (a property-guided diffusion model for anomaly repair) against a non-guided diffusion baseline. The comparison is made across four key metrics: Overall Improvement (Ms), Similarity (Ma), Localized Improvement (Mw), and Non-degradation (Mω). Results are shown for all anomaly categories within the VisA and MVTec-AD datasets, highlighting the median percentage improvement achieved by AR-Pro over the baseline for each metric.
In-depth insights#
Anomaly Repair#
Anomaly repair, a crucial aspect of anomaly detection, focuses on correcting anomalies rather than simply identifying them. This involves generating a counterfactual, a modified version of the anomalous input that conforms to the expected norm. The effectiveness of repair hinges on generating modifications that are both semantically meaningful and satisfy defined criteria, such as minimizing the deviation from the original input while ensuring the corrected version remains non-anomalous. This often requires a deep understanding of the underlying data and potentially sophisticated generative models like diffusion models to create these repairs. The formalization of desirable characteristics for successful repairs, such as preserving non-anomalous features while correcting only the anomalous ones, is critical for evaluating and comparing various methods. The practical applicability of anomaly repair is broad, spanning various domains like medical diagnosis, financial fraud detection, and industrial quality control, showcasing its potential for both enhancing model interpretability and facilitating effective decision-making.
Formal Explainability#
Formal explainability in anomaly detection seeks to move beyond qualitative assessments of model behavior. Instead, it aims for rigorous, mathematically defined properties that can be used to evaluate explanations. This approach addresses the inherent limitations of informal explanations, which often rely on subjective interpretations or heuristics. By establishing formal criteria, researchers can ensure that explanations are not only intuitive but also consistent and reliable. This rigor is particularly important in high-stakes scenarios such as medical diagnosis or fraud detection, where the consequences of erroneous interpretation could be severe. A key benefit of this formal approach is the potential for domain independence. Instead of relying on problem-specific metrics, a well-defined set of formal properties could serve as a universal standard for evaluating explainability, irrespective of the data modality or the underlying anomaly detection method. Such an approach facilitates cross-domain comparisons, promotes methodological transparency, and significantly boosts the overall trust and credibility of anomaly detection systems.
Diffusion Models#
Diffusion models represent a powerful class of generative models that have recently gained significant traction. They work by gradually adding noise to data until it becomes pure noise, then learning to reverse this process, thereby generating new data samples. A key advantage is their capacity to generate high-quality samples, often surpassing the capabilities of Generative Adversarial Networks (GANs). The process of progressively adding noise allows for a more controlled and stable training process, reducing the instability frequently associated with GANs. However, diffusion models can be computationally expensive, particularly during the training phase, requiring substantial computational resources. Furthermore, understanding and interpreting the underlying mechanisms of these models remains a challenge; their complex, multi-step process can make it difficult to fully grasp how they produce the generated output. Despite this, ongoing research is actively exploring improved training methods and enhancing their interpretability to further unlock their full potential in various applications, including image generation, time-series forecasting, and anomaly detection.
Empirical Results#
The Empirical Results section would ideally present a thorough quantitative analysis demonstrating the effectiveness of the proposed AR-Pro framework. This would involve showcasing improvements in anomaly repair quality across various metrics (Overall Improvement, Similarity, Localized Improvement, Non-degradation) compared to baseline methods. The results should be presented across diverse datasets (both vision and time-series) and anomaly detectors, highlighting the framework’s generalizability and robustness. Key performance indicators should include both mean and standard deviation, providing a clear picture of statistical significance. Further validation might involve qualitative analysis of the repairs, showcasing their semantic meaningfulness and visual plausibility. Importantly, the discussion should address any unexpected findings or variations in performance across different datasets or detectors, thereby providing a balanced and nuanced evaluation of AR-Pro’s capabilities.
Future Work#
Future research could explore several promising directions. Extending AR-Pro to handle more complex anomaly types beyond the linearly decomposable detectors would significantly broaden its applicability. Investigating alternative generative models, such as GANs or VAEs, could potentially improve repair quality and efficiency, providing a comparison to the diffusion-based approach used in this work. Developing more sophisticated property-based loss functions would refine the guidance of the repair process, leading to even more semantically meaningful and accurate counterfactual explanations. Additionally, the robustness of AR-Pro to noisy or incomplete data requires further investigation. Finally, applying AR-Pro to diverse real-world applications will be crucial in demonstrating its practical impact and identifying any limitations or unique challenges encountered in different domains.
More visual insights#
More on figures

This figure illustrates a reconstruction-based anomaly detection method. An anomalous input image (x) is fed into an encoder, which compresses it into a latent representation. This latent representation is then passed through a decoder to reconstruct the original image (x). The difference between the original and reconstructed images (x - x) represents the anomaly map, which highlights the anomalous regions. The anomaly score (s(x)) is calculated by summing up the squared differences between the original and reconstructed features. This demonstrates the concept of linear decomposability, where the overall anomaly score is a sum of individual feature-wise anomaly scores.

This figure illustrates the process of property-guided diffusion with masked in-filling used in the AR-Pro framework for anomaly repair. The process starts with an initial noise image (Xfix,T) and iteratively refines it through denoising steps. Each step incorporates property-based guidance to ensure the repair satisfies the defined properties (Overall Improvement, Similarity, Localized Improvement, and Non-degradation) and masked in-filling to preserve the non-anomalous parts of the original image. The process continues until a final repaired image (Xfix,0) is obtained. The figure shows the intermediate stages of the process, highlighting the iterative refinement towards a high-quality repair.

This figure shows a comparison of anomaly repair results between a baseline method and the proposed AR-Pro method on four PCB images. The first two columns display the original input images and their corresponding ground truth anomaly masks. The third column shows the results obtained using a baseline method, highlighting its failure to maintain similarity to the original input and properly repair the anomalies. The fourth column showcases the AR-Pro method’s results, demonstrating its ability to generate high-quality repairs that closely resemble the original inputs while effectively correcting the anomalies.

This figure shows visual comparisons of anomaly repairs generated by AR-Pro and a baseline method on the MVTec dataset. It visually demonstrates AR-Pro’s ability to produce repairs that maintain a greater similarity to the original input image compared to the baseline, highlighting the effectiveness of the property-guided diffusion approach in preserving semantic meaning.

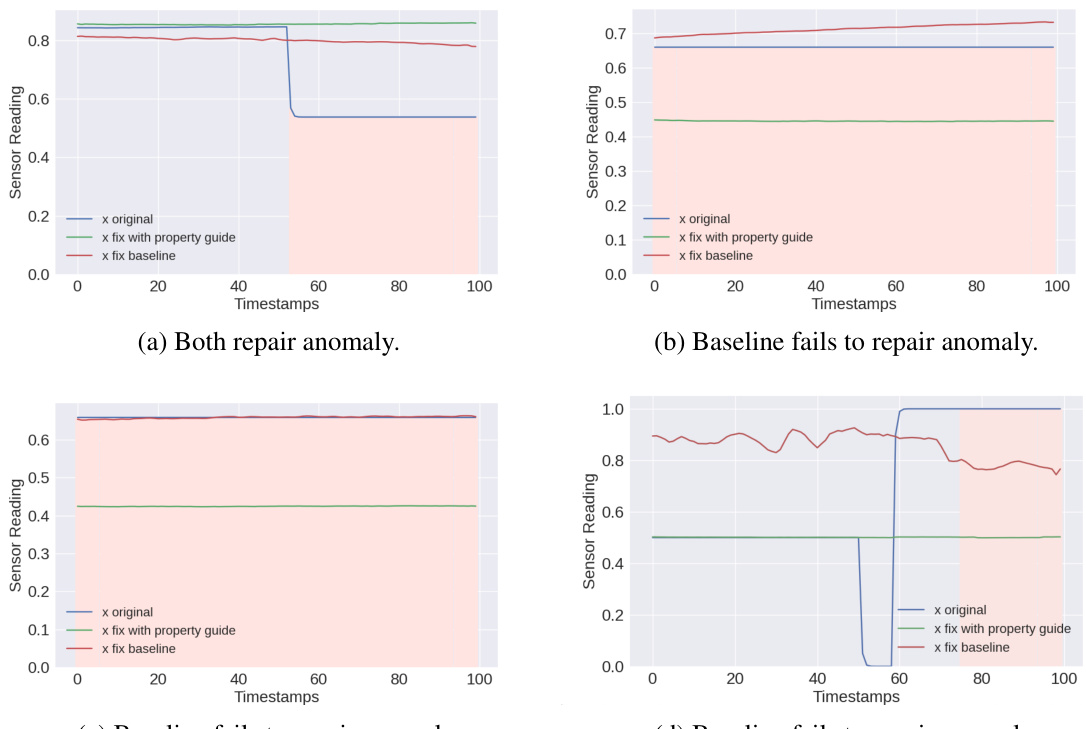
This figure displays four time-series plots comparing the performance of AR-Pro (property-guided repair) against a baseline method in repairing anomalies. Each plot shows an original time series (blue), a repaired time series using AR-Pro (green), and a repaired time series using the baseline method (red). The plots illustrate scenarios where: (a) both methods successfully repair the anomaly, (b) the baseline fails to repair the anomaly while AR-Pro does, and (c,d) the baseline method creates a spurious signal or fails to effectively repair the anomaly. The figure demonstrates the effectiveness of the AR-Pro method, highlighting its superior ability to generate accurate, semantically meaningful repairs.

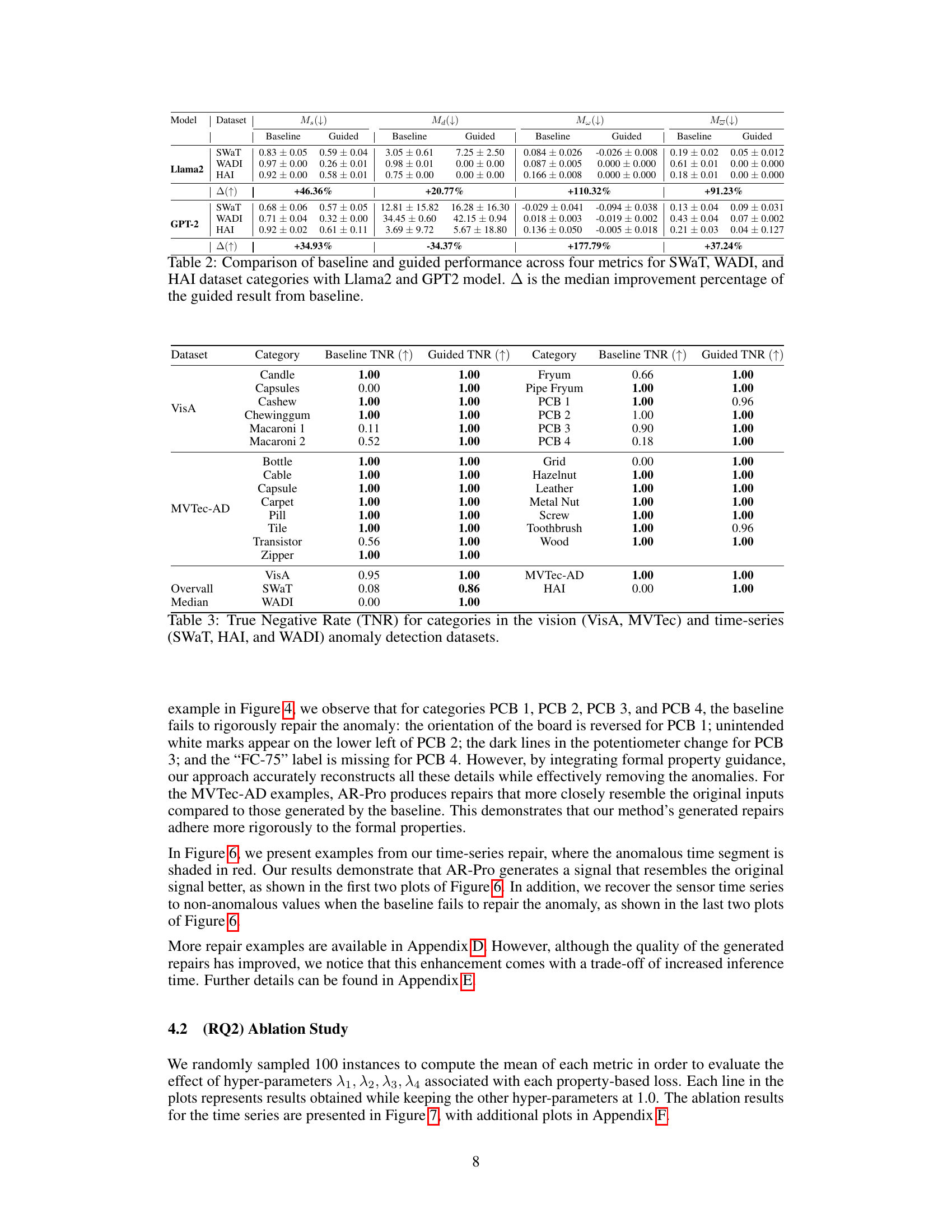
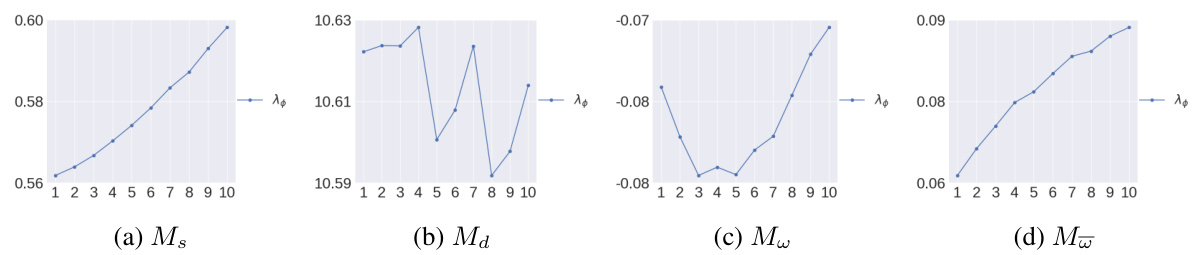
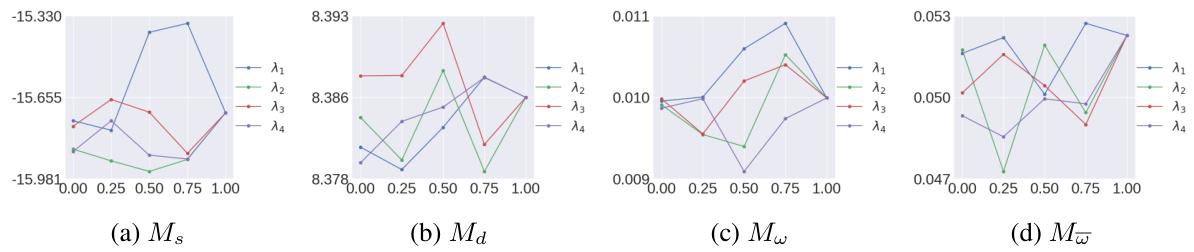
This figure displays ablation study results, specifically the effect of varying hyperparameters (λ1, λ2, λ3, λ4) on four different metrics (Ms, Md, Mw, Mw). Each subplot shows how changing one hyperparameter while keeping others constant influences the corresponding metric. The x-axis represents the hyperparameter values, and the y-axis represents the metric values. This illustrates the sensitivity and robustness of the anomaly repair process with respect to hyperparameter tuning.

This figure shows several examples from the VisA dataset to visually compare the anomaly repair results generated by AR-Pro against a baseline method. Each example shows the original image, a mask highlighting the anomalous region, the repaired image from the baseline method, and the repaired image from AR-Pro. The comparison highlights AR-Pro’s ability to generate repairs that closely resemble the original, non-anomalous version of the images, better than the baseline approach.

This figure presents a comparison of anomaly repair results between the AR-Pro framework and a baseline method on the MVTec dataset. It visually demonstrates that AR-Pro produces repairs that are more similar to the original, non-anomalous inputs compared to the baseline. The differences are highlighted to illustrate the improvements in visual fidelity and semantic preservation achieved by AR-Pro.

This figure showcases visual anomaly repair results on the MVTec dataset using AR-Pro. It compares the repairs generated by AR-Pro to those of a baseline method, demonstrating AR-Pro’s ability to generate repairs that are more visually similar to the original, non-anomalous images. The differences highlight how AR-Pro’s property-guided approach leads to higher-quality repairs that maintain better visual fidelity.
This figure illustrates the process of property-guided diffusion with masked in-filling used in the AR-Pro framework. It shows how the model iteratively refines a noisy input (xfix,T) towards a high-quality repair (xfix). Each step involves a denoising process guided by property-based losses, ensuring that the repair satisfies specific criteria (overall improvement, similarity, localized improvement, and non-degradation). Masked in-filling helps preserve the non-anomalous regions during the repair process. The overall flow is from a noisy initial state to a refined repair that aligns with the desired properties.
This figure shows the process of property-guided diffusion with masked in-filling used in the AR-Pro framework. It depicts a sequence of steps: first, denoising steps are performed on an anomalous input image; then, property-based guidance is applied to nudge the iterations towards a high-quality repair; finally, masked in-filling ensures that non-anomalous regions are preserved during the process. The output is a repaired image (xfix) which serves as a counterfactual explanation for the anomaly.
This figure illustrates the AR-Pro framework, a method for generating counterfactual explanations for anomaly repair. The process begins by identifying an input’s anomalous region using an anomaly detector. Then, a property-guided diffusion model is used to repair the anomalous region, creating a counterfactual example of what a non-anomalous version should look like. Four key properties guide the repair process: overall improvement (lower anomaly score), similarity to the original input, localized improvement (score in the repaired area improves), and non-degradation (score in the non-anomalous area does not worsen significantly).

This figure provides a high-level overview of the AR-Pro framework, which uses a generative model to repair anomalies and offers counterfactual explanations. The process begins with the identification of anomalous regions in the input, followed by the use of property-guided diffusion to produce a repair. This repair acts as the counterfactual explanation for the anomaly. The effectiveness of the repair is evaluated based on four key properties that ensure its quality and relevance as an explanation: overall improvement, similarity, localized improvement, and non-degradation. These properties are defined with respect to a linearly decomposable anomaly detector, making the evaluation domain-independent.
More on tables
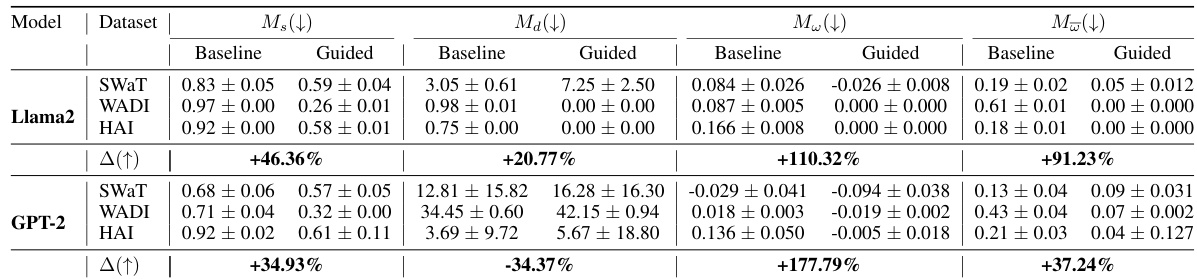
This table presents a quantitative comparison of the performance of AR-Pro (a property-guided diffusion model for anomaly repair) against a non-guided diffusion baseline. The comparison is made across four key metrics: Overall Improvement, Similarity, Localized Improvement, and Non-degradation. Results are shown for all categories within the VisA and MVTec-AD datasets, highlighting the median percentage improvement achieved by AR-Pro over the baseline for each metric.

This table presents a quantitative comparison of the performance of AR-Pro against a non-guided diffusion baseline across four key metrics (Overall Improvement, Similarity, Localized Improvement, and Non-degradation) for anomaly repair. The results are broken down by image category within the VisA and MVTec-AD datasets, showcasing the median percentage improvement achieved by AR-Pro over the baseline for each metric. The table highlights the consistent superior performance of the proposed AR-Pro framework in improving the quality of anomaly repairs.

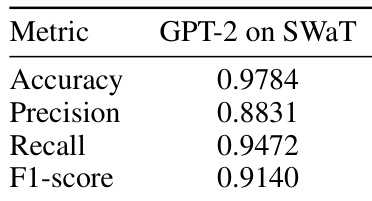
This table presents the Area Under the Receiver Operating Characteristic (AUROC) scores achieved by the FastFlow anomaly detection model on various categories within the VisA dataset. Two AUROC scores are provided for each category: one for image-level anomaly detection and another for pixel-level anomaly detection. The average AUROC scores across all categories are also shown.
This table presents a quantitative comparison of the performance of AR-Pro (property-guided diffusion) against a non-guided diffusion baseline across four metrics (Overall Improvement, Similarity, Localized Improvement, and Non-degradation). The results are shown for all the categories within the VisA and MVTec-AD datasets. The Δ column indicates the median percentage improvement achieved by AR-Pro over the baseline for each metric.

This table presents a comparison of the performance of AR-Pro against a baseline non-guided diffusion model across four metrics (Overall Improvement, Similarity, Localized Improvement, and Non-degradation) for various categories within the VisA and MVTec-AD datasets. The median percentage improvement achieved by AR-Pro over the baseline is also reported, highlighting its superior performance in generating high-quality anomaly repairs.
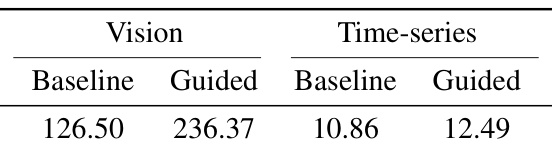
This table presents a comparison of the median inference times for both baseline and guided diffusion models in the vision and time-series anomaly repair tasks. The results highlight the trade-off between repair quality and computational cost, demonstrating the increase in runtime associated with the property-guided approach, especially in vision tasks.
Full paper#