↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Equivariant Graph Neural Networks (GNNs) are powerful tools for analyzing 3D geometric data, but their effectiveness can be hampered by the use of low-degree representations. Existing models often simplify computations by focusing on Cartesian vectors, which can lead to a loss of important information, especially when dealing with symmetries found in many scientific datasets. This paper demonstrates that these simplifications come at the cost of expressiveness.
To address this issue, the authors introduce HEGNN, a new GNN that incorporates higher-degree representations while maintaining computational efficiency. HEGNN uses a scalarization trick similar to EGNN, which simplifies computations but without sacrificing the richness of high-degree representations. Their theoretical analysis and extensive experiments demonstrate that HEGNN significantly improves performance on datasets with and without obvious symmetries.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with equivariant graph neural networks (GNNs), especially in scientific applications dealing with symmetric structures. It challenges the common assumption that high-degree representations are unnecessary, offering theoretical and experimental evidence for their importance. The proposed HEGNN model improves efficiency and accuracy, opening new avenues for research in this critical area.
Visual Insights#

This figure displays various symmetric graph structures, including odd and even k-fold rotations, tetrahedron, cube (hexahedron), octahedron, dodecahedron, and icosahedron. The caption highlights a key finding from the paper: equivariant graph neural networks (GNNs) operating on these symmetric graphs will produce a zero function output if the degree of their representation is fixed at 1. This illustrates a limitation of certain GNN models and motivates the research presented in the paper.

This table summarizes the theoretical findings on the expressivity degeneration of equivariant GNNs applied to symmetric graphs. It lists several common symmetric graph structures (k-fold rotations and regular polyhedra), their corresponding symmetry groups, and the degrees (l) of output representations that will always cause the equivariant GNN to degenerate to a zero function. The table highlights the limitations of using only low-degree representations in equivariant GNNs, especially when dealing with symmetric data.
In-depth insights#
Equivariant GNN Expressivity#
The expressivity of equivariant graph neural networks (GNNs) is a crucial aspect determining their ability to effectively model geometric data. Equivariant GNNs leverage symmetries inherent in the data, such as rotational or translational invariance, to improve efficiency and generalization. However, the choice of representation degree significantly impacts expressivity. Lower-degree representations, while computationally efficient, may limit the network’s ability to capture complex relationships within the data, especially in the presence of symmetric structures. Higher-degree representations offer greater expressiveness but come with increased computational costs. The optimal balance hinges on the trade-off between computational demands and the need for sufficient expressiveness to accurately model the given task and data characteristics. Theoretical analyses are crucial for understanding this trade-off and for designing more expressive yet computationally feasible equivariant GNN architectures. Furthermore, the effect of symmetry, or lack thereof, within the data on the network’s expressive power requires careful consideration. Symmetric datasets pose a unique challenge, as certain representation degrees may cause the network to degenerate to a trivial function, highlighting the need for careful selection and potential augmentation of the representational framework.
HEGNN Architecture#
The HEGNN architecture likely builds upon existing equivariant graph neural networks (GNNs), such as EGNN, but enhances them by incorporating high-degree steerable representations. This addresses a key limitation of simpler models like EGNN, which restrict message passing to first-degree steerable features (3D vectors), leading to reduced expressivity, especially on symmetric structures. HEGNN likely uses a scalarization trick similar to EGNN for efficient message passing between different degrees. This likely involves encoding high-degree features into scalars, performing invariant message passing operations, and then recovering orientation information. The architecture might comprise multiple layers, each iteratively refining representations with a combination of high-degree and low-degree features. The aggregation mechanism may involve techniques like inner products or Clebsch-Gordan coefficients, depending on the specific design choices made to balance expressiveness and computational cost. A readout layer would likely be included to produce graph-level representations. Overall, HEGNN’s design aims to offer a balance between the efficiency of scalarization approaches and the increased expressivity obtained from incorporating high-degree features.
Symmetric Graph Analysis#
Symmetric graph analysis within the context of equivariant graph neural networks (GNNs) focuses on understanding how these networks behave when processing graphs exhibiting inherent symmetries. The core idea is that the presence of symmetry can significantly impact the network’s expressive power and computational efficiency. Analyzing symmetric graphs helps reveal potential limitations, particularly where a GNN might fail to distinguish between different orientations of an identical symmetric structure. This necessitates careful consideration of the degree of steerable features used in the GNN, as specific degrees might cause the network’s output to collapse to a trivial result (zero function) for certain symmetric graphs, regardless of the input’s orientation. Therefore, theoretical analysis using group theory is crucial to determine when a GNN would degenerate in its expressive power. The exploration of symmetric graphs (such as k-fold rotations and regular polyhedra) enables a rigorous mathematical examination of expressiveness limitations. Furthermore, this analysis guides the design and improvement of GNNs, potentially leading to new models that effectively utilize high-degree representations while maintaining efficiency. This investigation of symmetric structures is vital for advancing the field of equivariant GNNs.
High-Degree Benefits#
The concept of “High-Degree Benefits” in the context of equivariant graph neural networks (EGNNs) centers on the idea that incorporating higher-degree representations can significantly boost the model’s expressiveness and performance. Lower-degree models, while computationally efficient, may struggle to capture the complexities of geometric relationships in scientific data like molecular structures. Higher-degree representations, such as those using spherical harmonics, provide a richer encoding of rotational symmetries, allowing the network to learn more nuanced relationships and improve accuracy, particularly on datasets with intricate geometric patterns. However, this increased expressiveness comes at the cost of increased computational complexity. The “High-Degree Benefits” discussion within the paper likely weighs the trade-offs between expressivity and efficiency, exploring whether the performance gains from using higher-degree representations outweigh their computational burden. The effectiveness of high-degree representations might also depend on the specific dataset, with symmetrical structures potentially benefiting the most from their enhanced expressive power while less-symmetrical datasets might show more modest improvements or even no advantage. The paper likely demonstrates how careful design and techniques, such as scalarization methods, can mitigate some of the computational overhead associated with higher-degree approaches, making them a practical choice for certain applications.
Future Research#
Future research directions stemming from this paper could explore several promising avenues. Extending HEGNN to handle larger-scale datasets and more complex molecular systems is crucial for real-world applicability. Investigating the impact of different scalarization techniques and high-degree representation choices on the model’s performance would provide valuable insights. Developing a more comprehensive theoretical understanding of expressivity in equivariant GNNs, beyond symmetric structures, is vital to guide future model design and analysis. Exploring alternative ways to incorporate high-degree information without the computational overhead of traditional methods, such as leveraging efficient tensor operations or novel network architectures, should be prioritized. Finally, assessing the robustness of HEGNN against noisy data and different types of graph perturbations is necessary for practical deployment. This research lays a strong foundation for future advancements in equivariant GNNs and their applications in various scientific domains.
More visual insights#
More on tables
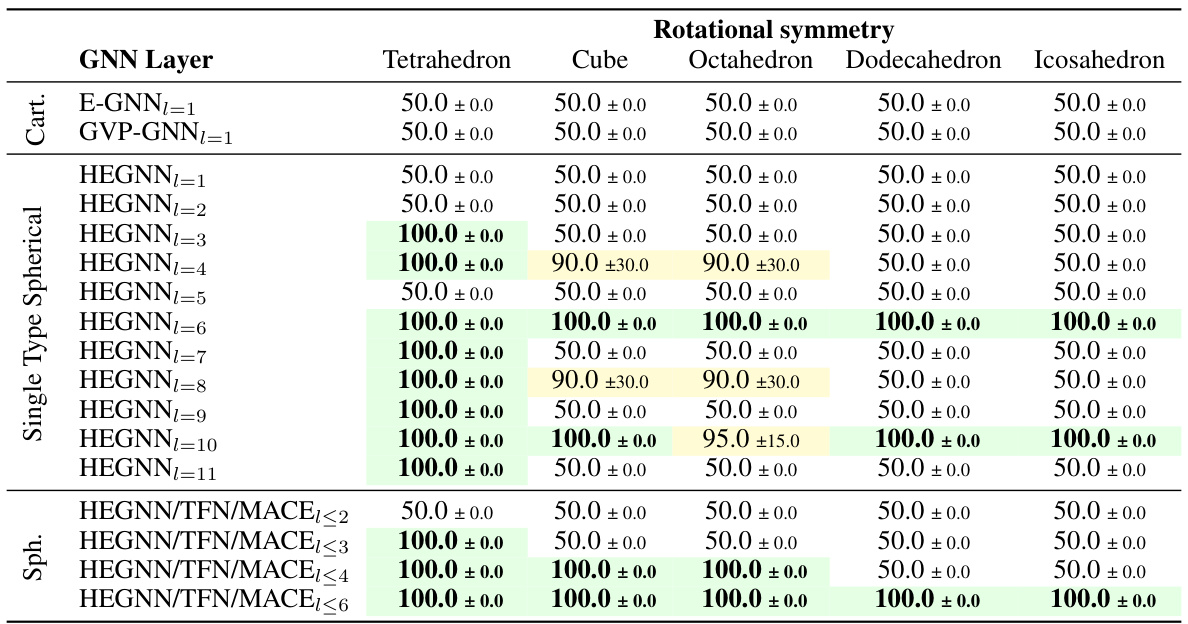
This table presents the results of an experiment on regular polyhedra to test the ability of different equivariant graph neural networks to distinguish between an original symmetric structure and a rotated version of the same structure. The table shows the accuracy (in %) of various GNN models in distinguishing these two states for different regular polyhedra, varying the degree of steerable features used. The results demonstrate the impact of high-degree representations on the expressivity of equivariant GNNs on symmetric structures.
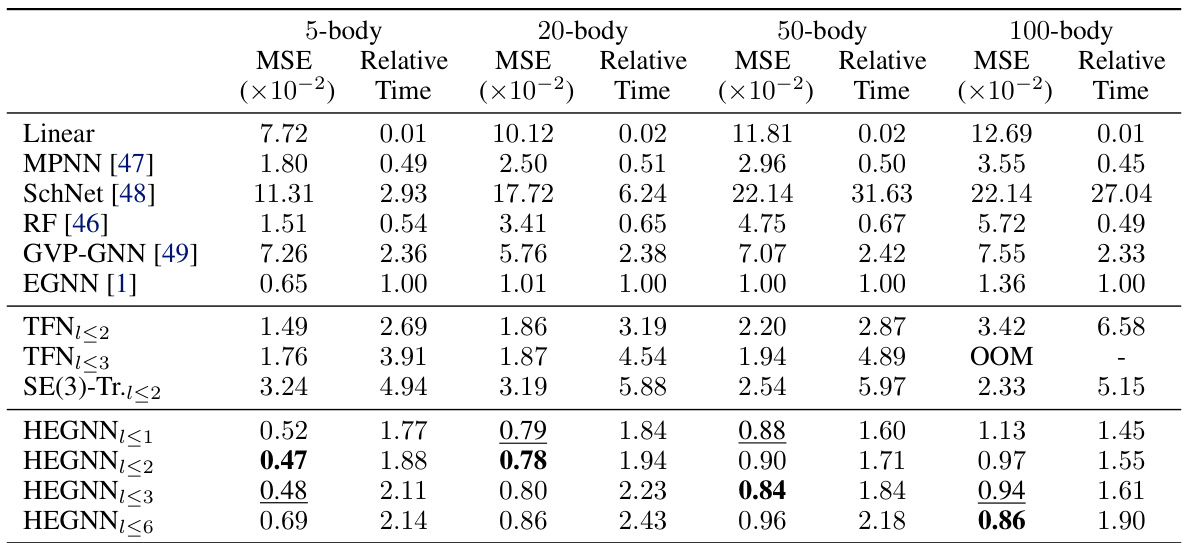
This table presents a comparison of the Mean Squared Error (MSE) and relative computation time of different models on the N-body system simulation task. The MSE is a measure of the accuracy of the models’ predictions, while the relative time indicates how much longer each model takes to run compared to EGNN. Lower MSE values and relative times closer to 1.00 are better.
This table presents the results of an experiment on regular polyhedra to evaluate the expressivity of different equivariant GNN models. The accuracy of each model in distinguishing between the original graph and a rotated version is measured, demonstrating the necessity of incorporating high-degree representations for improved performance.

This table presents the results of a perturbation experiment conducted to assess the robustness of three different models (EGNN, HEGNNl=3, and HEGNNl≤3) against noise perturbations. The experiment used a tetrahedron as an example, adding noise with different ratios (ε = 0.01, 0.05, 0.10, 0.50). The results show the performance of each model under different noise levels and demonstrate the better robustness of HEGNN with high-degree steerable features, particularly compared to EGNN.

This table presents a summary of the theoretical analysis of the expressivity of equivariant GNNs on symmetric graphs. It shows which symmetry groups lead to expressivity degeneration (i.e., the output of the GNN becomes a zero function) for specific output degrees (l) of the steerable features. The table considers k-fold rotations (for both even and odd k), tetrahedron, cube/octahedron, and dodecahedron/icosahedron, listing the relevant symmetry group (H) and the values of l that result in degeneration for each.

This table presents the traces of the Wigner-D matrices for various symmetric groups, including cyclic, dihedral, tetrahedral, octahedral, and icosahedral groups. The traces are calculated using a formula involving the degree l and the parameters r and b, specific to each group type. The formula is illustrated with an example for the tetrahedral group. This data is used in Theorem 3.6 to determine when the equivariant GNNs on symmetric graphs will degenerate to a zero function.
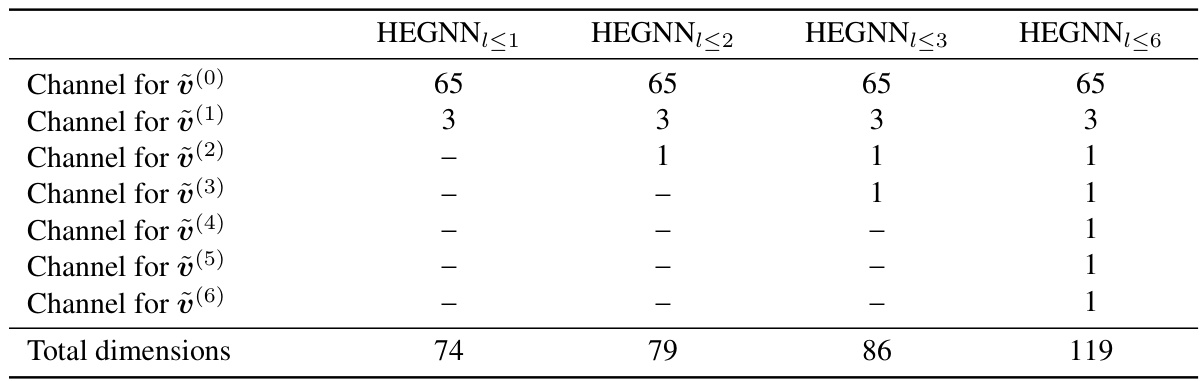
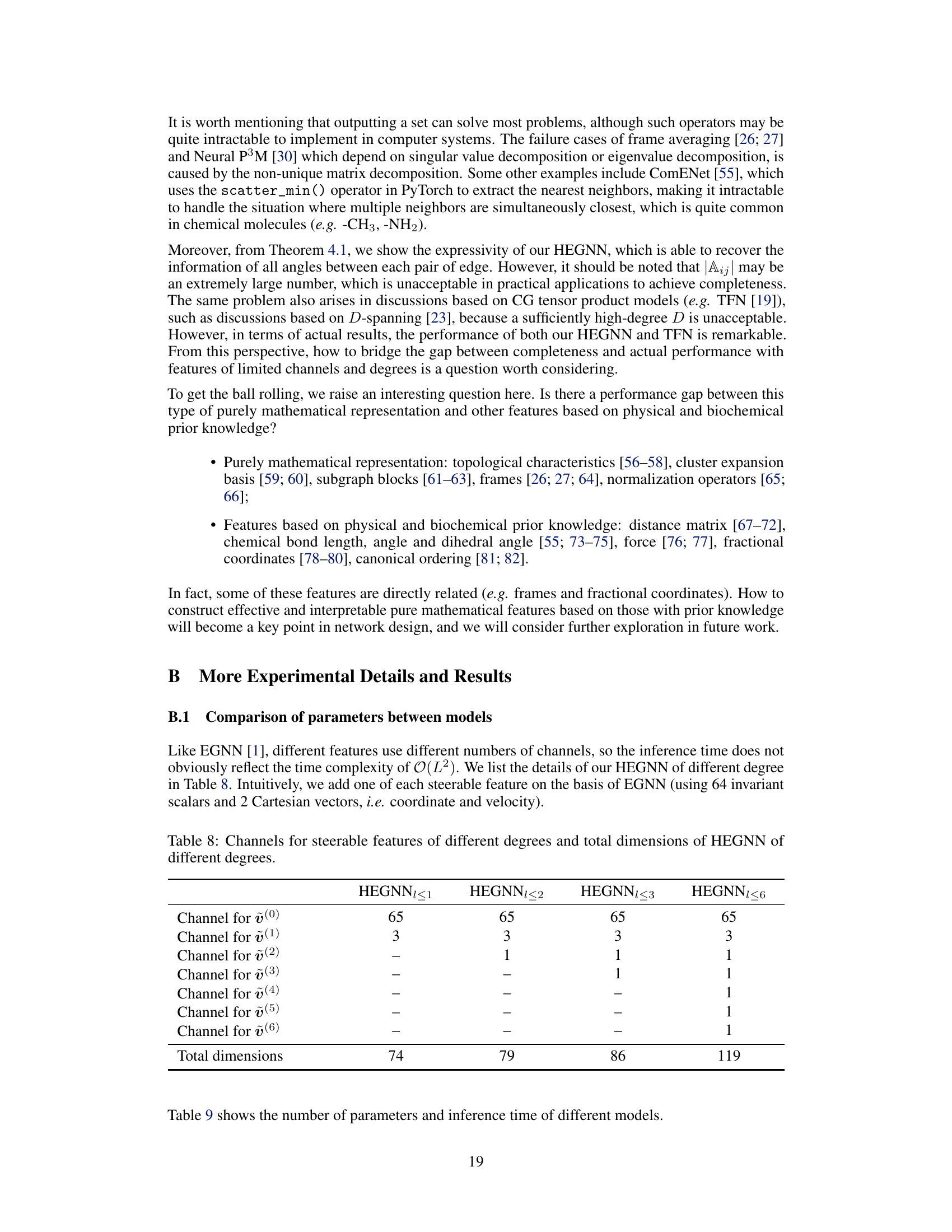
This table shows the number of channels used for each degree of steerable features in the HEGNN model. The model uses invariant scalars (0th degree), Cartesian vectors (1st degree), and higher-degree steerable features (2nd degree and above). The total dimensions represent the total number of features used in each version of the model. The different versions of HEGNN (HEGNN≤1, HEGNN≤2, HEGNN≤3, HEGNN≤6) differ in the maximum degree of steerable features they incorporate.
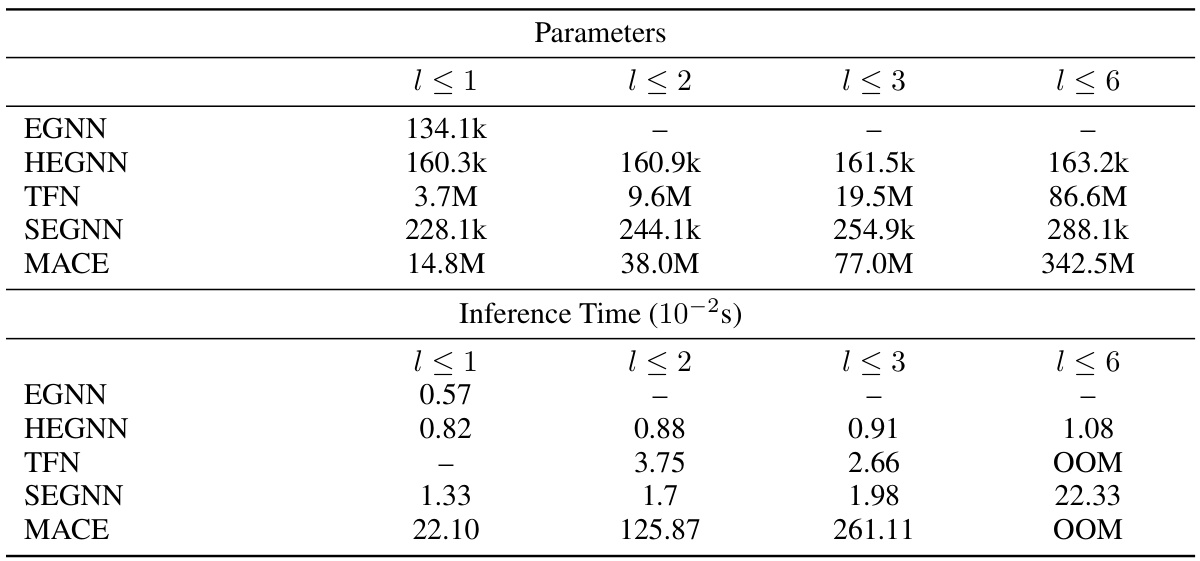
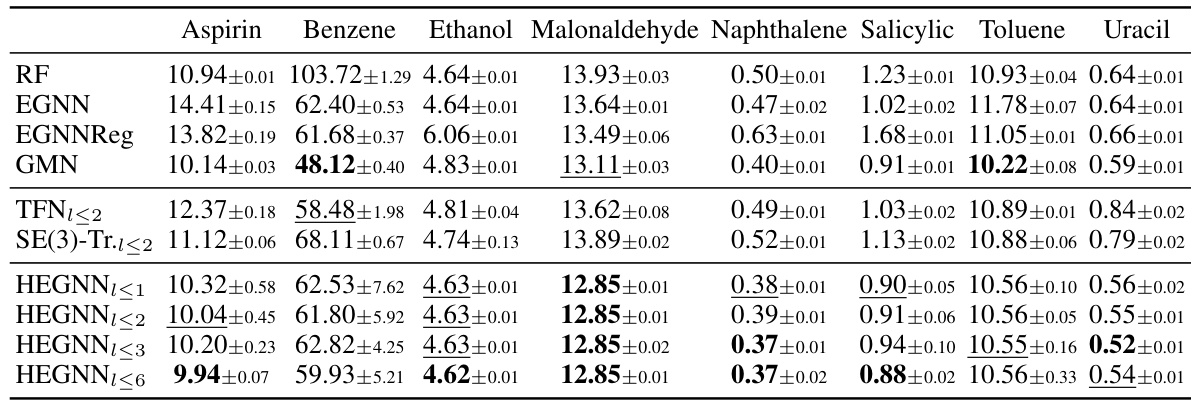
This table compares the number of parameters and inference time of several models on a 100-body dataset. The models compared include EGNN, HEGNN (with varying degrees of steerable features), TFN, SEGNN, and MACE. The table shows that HEGNN achieves a good balance between efficiency and accuracy, outperforming other high-degree models in inference time while maintaining a reasonable parameter count.

This table presents the results of an experiment designed to test the expressivity of various equivariant GNN models on k-fold symmetric structures. The models tested include EGNN, GVP-GNN, and HEGNN variants with varying degrees (l) of steerable features. The table shows the accuracy (%) of each model in distinguishing between a rotated and unrotated k-fold structure for k=2,3,5,10. The results demonstrate the improved expressive power of HEGNN, especially when higher-degree steerable features are incorporated.

This table shows when an equivariant GNN will degenerate to a zero function on symmetric graphs. It lists various symmetric graphs (k-fold, tetrahedron, cube/octahedron, dodecahedron/icosahedron) and their corresponding symmetry groups. For each graph, the table indicates the values of the output degree (l) that will lead to the GNN outputting a zero function. This highlights the limitations of using only low-degree representations in equivariant GNNs for these symmetric structures.

This table shows the accuracy of different equivariant GNN models on distinguishing between a regular polyhedron and its rotated version. The models tested include those using only Cartesian vectors (EGNN and GVP-GNN) and those using high-degree steerable features (TFN, MACE, and HEGNN). The results show that models using only Cartesian vectors fail to distinguish the two versions, while models using high-degree steerable features show varying levels of success, with HEGNN exhibiting the best performance. The accuracy is given as a percentage, indicating the model’s ability to correctly classify the two graph configurations.
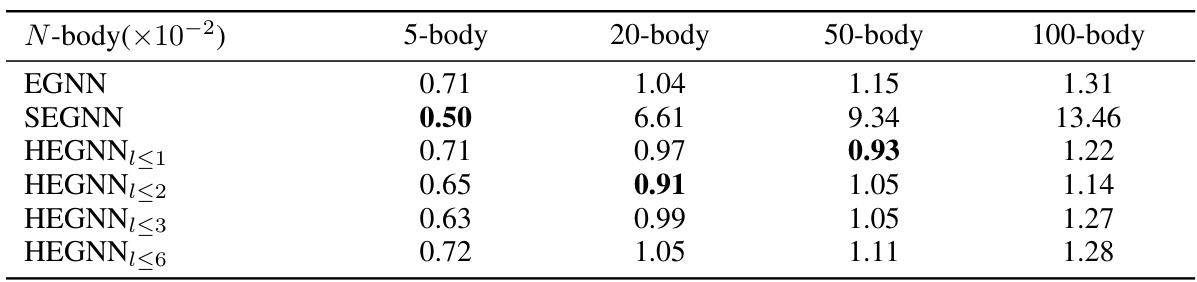
This table presents the Mean Squared Error (MSE) and relative time-consuming ratio compared to EGNN for different models on N-body systems with varying numbers of particles (5, 20, 50, 100). The relative time is calculated by dividing the inference time of each model by the inference time of EGNN. Lower MSE indicates better performance, while a lower relative time indicates faster computation.

This table presents the accuracy of various equivariant GNN models in distinguishing between rotated and unrotated versions of regular polyhedra. It demonstrates the impact of using Cartesian vectors only (EGNN, GVP-GNN) versus incorporating higher-degree steerable vectors (HEGNN, TFN/MACE). The results show that models only using Cartesian vectors (1st-degree representations) fail to differentiate rotated from unrotated polyhedra, while high-degree models achieve better accuracy, aligning with the theoretical findings of the paper.

This table presents a comparison of the Mean Squared Error (MSE) and relative computation time of different models on the N-body system dataset. The relative time is calculated with respect to EGNN, which is set as the baseline. The table shows the performance of various models for different sizes of the N-body system (5, 20, 50, and 100 bodies). The results highlight HEGNN’s superior performance and efficiency compared to other models.
Full paper#