↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) enables collaborative model training without direct data sharing. However, existing data augmentation techniques in FL often compromise privacy by sharing input-level or feature-level data. This paper introduces FedAvP, which addresses these privacy concerns by sharing only augmentation policies. This innovative approach enhances data security and efficiency.
FedAvP achieves this through a novel Federated Meta-Policy Loss (FMPL), which interprets policy loss as a meta update loss in standard FL. By utilizing first-order gradient information, FedAvP improves privacy and reduces communication costs. Furthermore, FedAvP employs a meta-learning approach to efficiently search for personalized and adaptive policies tailored to each client’s specific data distribution. Benchmark results demonstrate that FedAvP surpasses existing augmentation methods and federated learning algorithms, especially in scenarios with heterogeneous data.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical challenge of data privacy in federated learning (FL) by proposing FedAvP, a novel algorithm that shares only augmentation policies instead of data itself. This significantly enhances privacy while improving model performance, particularly in heterogeneous FL settings. FedAvP’s use of a first-order approximation of the meta-policy gradient improves efficiency and reduces communication costs. The adaptive policy search method also allows personalization for diverse clients and outperforms existing FL and data augmentation methods. The research is relevant to current trends in secure and efficient FL, opening avenues for future research in privacy-preserving FL techniques and adaptive policy search algorithms.
Visual Insights#

This figure illustrates the FedAvP algorithm’s workflow. Panel (a) shows the federated meta-policy optimization, where the server distributes global model parameters and policy parameters to clients. Clients then augment their local data and update their local models. These updates are aggregated at the server to produce the updated global model. Next, clients use the updated global model to update their local policies, which are aggregated at the server. Panel (b) presents a simplified first-order approximation of this process, to improve privacy and reduce communication overhead.
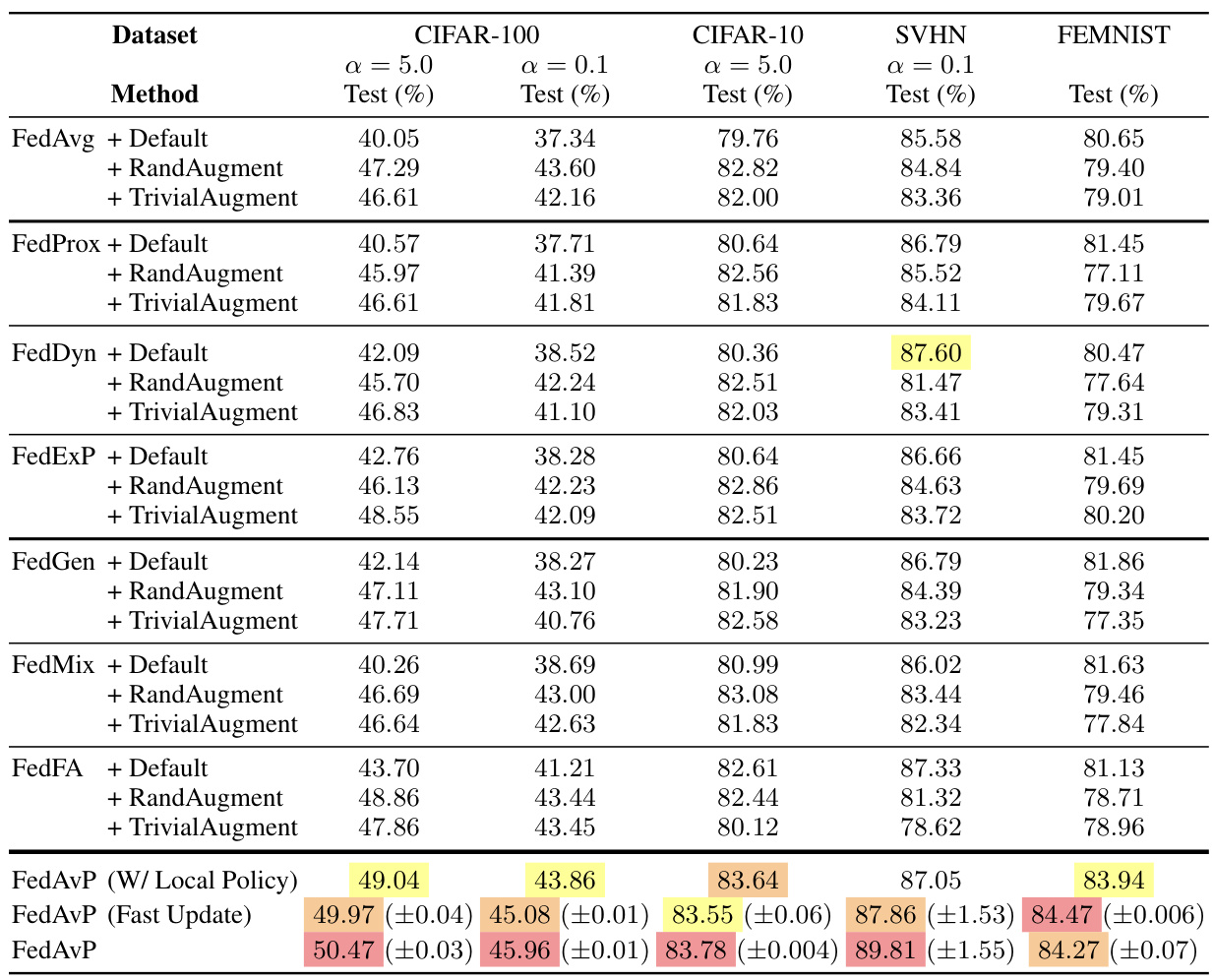
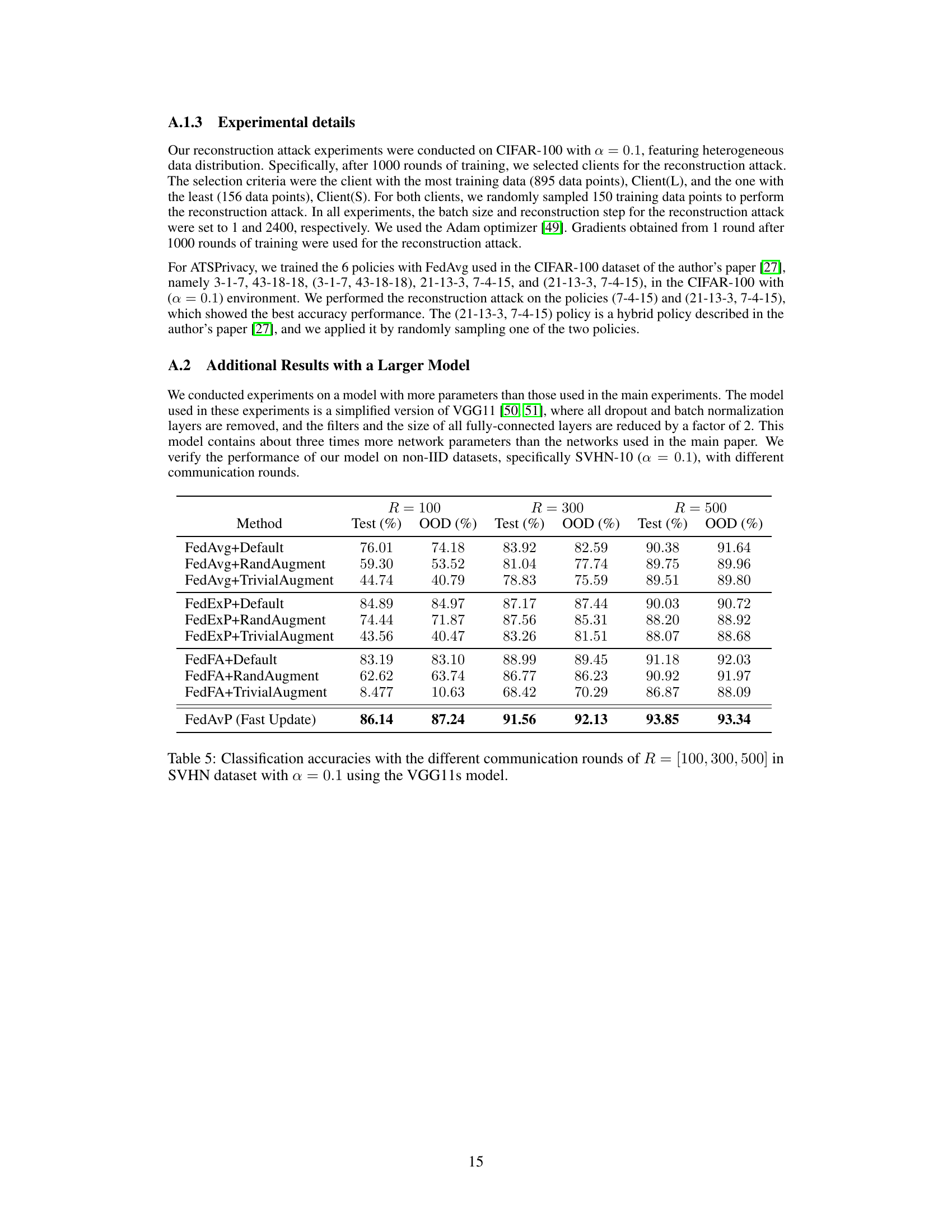
This table presents the classification accuracy results for various federated learning algorithms across four datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The algorithms tested include FedAvg, FedProx, FedDyn, FedExP, FedGen, FedMix, and FedFA, each with and without additional data augmentation techniques (RandAugment and TrivialAugment). The table also shows results for the proposed FedAvP algorithm with and without its fast update optimization, and for a variant that uses a local policy only. Results are averages over three random seeds, with standard deviations included for the FedAvP results.
In-depth insights#
FedAvg Enhancements#
In federated learning, FedAvg is a foundational algorithm, but its performance can be limited by data heterogeneity and communication costs. FedAvg enhancements focus on addressing these issues. Common approaches include improving the model aggregation process, employing techniques like FedProx to handle client heterogeneity more effectively, and using more efficient communication strategies such as quantization or sparsification. Addressing data heterogeneity is crucial. Methods often involve personalized or federated data augmentation techniques or algorithms to adapt to different data distributions across clients, thus improving generalization and accuracy. Reducing communication overhead is also critical, especially in resource-constrained environments. Strategies involving local model updates, differential privacy, or compression techniques are frequently used. Research continues to explore new and innovative ways to enhance the core FedAvg algorithm’s performance and efficiency, moving toward more robust and practical federated learning systems. Combining multiple techniques is often the most effective approach, creating a comprehensive strategy to improve FedAvg’s overall utility in diverse and challenging settings.
Policy Gradient Methods#
Policy gradient methods are a crucial part of reinforcement learning, offering a direct approach to optimizing an agent’s policy. Instead of explicitly calculating the optimal policy, these methods use gradient ascent to iteratively improve the policy’s performance. The core idea involves estimating the gradient of the expected reward with respect to the policy parameters. This gradient indicates the direction in which to adjust the policy parameters to maximize the expected return. There exist various methods for estimating the policy gradient, including Monte Carlo methods, temporal difference learning, and actor-critic methods. Each method has trade-offs in terms of bias-variance, computational cost, and data efficiency. A key challenge lies in effectively estimating the gradient, which often involves high variance due to the stochastic nature of reinforcement learning. Techniques like variance reduction and importance sampling are commonly employed to address this challenge. Furthermore, the choice of policy parameterization greatly impacts the performance and effectiveness of the method. The selection of a suitable policy architecture and the design of the policy update rule are critical considerations. Advanced techniques such as trust region methods are used to stabilize the training process and prevent drastic policy changes. Finally, policy gradient methods are particularly suitable for continuous action spaces and complex environments where traditional dynamic programming approaches may be intractable.
Heterogeneous FL#
Heterogeneous Federated Learning (FL) presents unique challenges compared to the idealized homogeneous setting. Data heterogeneity, where clients possess non-identically distributed data, is a core issue, impacting model accuracy and generalization. System heterogeneity, encompassing differences in client devices, network conditions, and computational capabilities, further complicates training. Effective heterogeneous FL necessitates algorithms robust to data imbalances and capable of adapting to varying resource constraints. Techniques like personalized federated learning, adaptive learning rates, and novel aggregation strategies aim to address these challenges, enhancing fairness and efficiency. However, privacy concerns remain paramount; data heterogeneity can exacerbate privacy risks, demanding careful consideration of algorithm design and security protocols. Future research should focus on developing more efficient and privacy-preserving algorithms that explicitly account for both data and system heterogeneity in FL.
Privacy-Preserving Augmentation#
Privacy-preserving data augmentation in federated learning (FL) tackles the challenge of improving model accuracy while upholding data confidentiality. Existing methods often share data-related information during augmentation, creating privacy vulnerabilities. A key focus is on developing techniques that share only essential information, such as augmentation policies, not the raw data itself. This approach minimizes the risk of reconstruction attacks and reduces communication overhead. Effective strategies include employing meta-learning to adapt augmentation policies to heterogeneous data distributions across clients, and using efficient policy search methods to find optimal augmentation strategies without compromising privacy. The ultimate goal is to balance the benefits of data augmentation with robust privacy protections in FL environments. This involves careful consideration of potential attack vectors and the development of sophisticated defenses.
Future Work: Scalability#
Future work on scalability for federated learning (FL) systems is crucial. Addressing the increasing number of clients and the heterogeneity of their data distributions is paramount. This requires investigation into more efficient aggregation techniques, potentially exploring decentralized aggregation or hierarchical structures. Improving the robustness of the system to stragglers (slow or unresponsive clients) is also important, perhaps through techniques like asynchronous updates or adaptive resource allocation. Further research into reducing communication overhead, for example by using model compression or differential privacy methods, is needed. Finally, evaluating and optimizing the performance of the system across diverse network conditions and hardware capabilities is key to making federated learning truly scalable for widespread deployment.
More visual insights#
More on figures
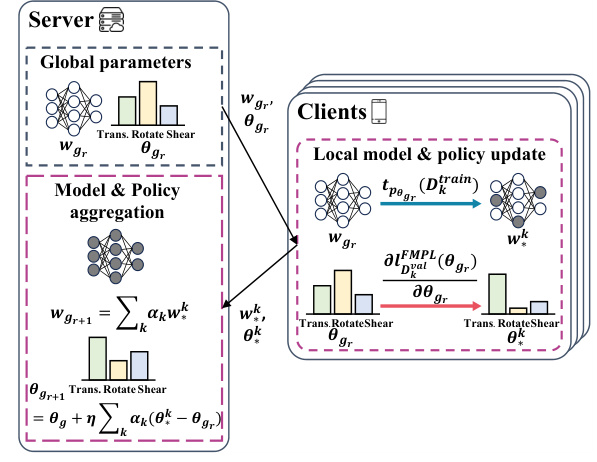
This figure illustrates the FedAvP algorithm’s workflow. Panel (a) shows the federated meta-policy loss method, where the server distributes global model and policy parameters to clients. Clients train locally on augmented data, updating both their local models and policies. These are then aggregated by the server to update the global model and policy. Panel (b) shows a first-order approximation of this process, simplifying the calculation and reducing communication costs by approximating the meta-policy gradient.

This figure illustrates the FedAvP algorithm’s workflow. Panel (a) shows the federated meta-policy optimization where the server distributes global model and policy parameters to clients, who then locally train models with augmented data and send updates back for aggregation. Panel (b) depicts a faster, first-order approximation of this process, still involving local model and policy updates followed by aggregation on the server.

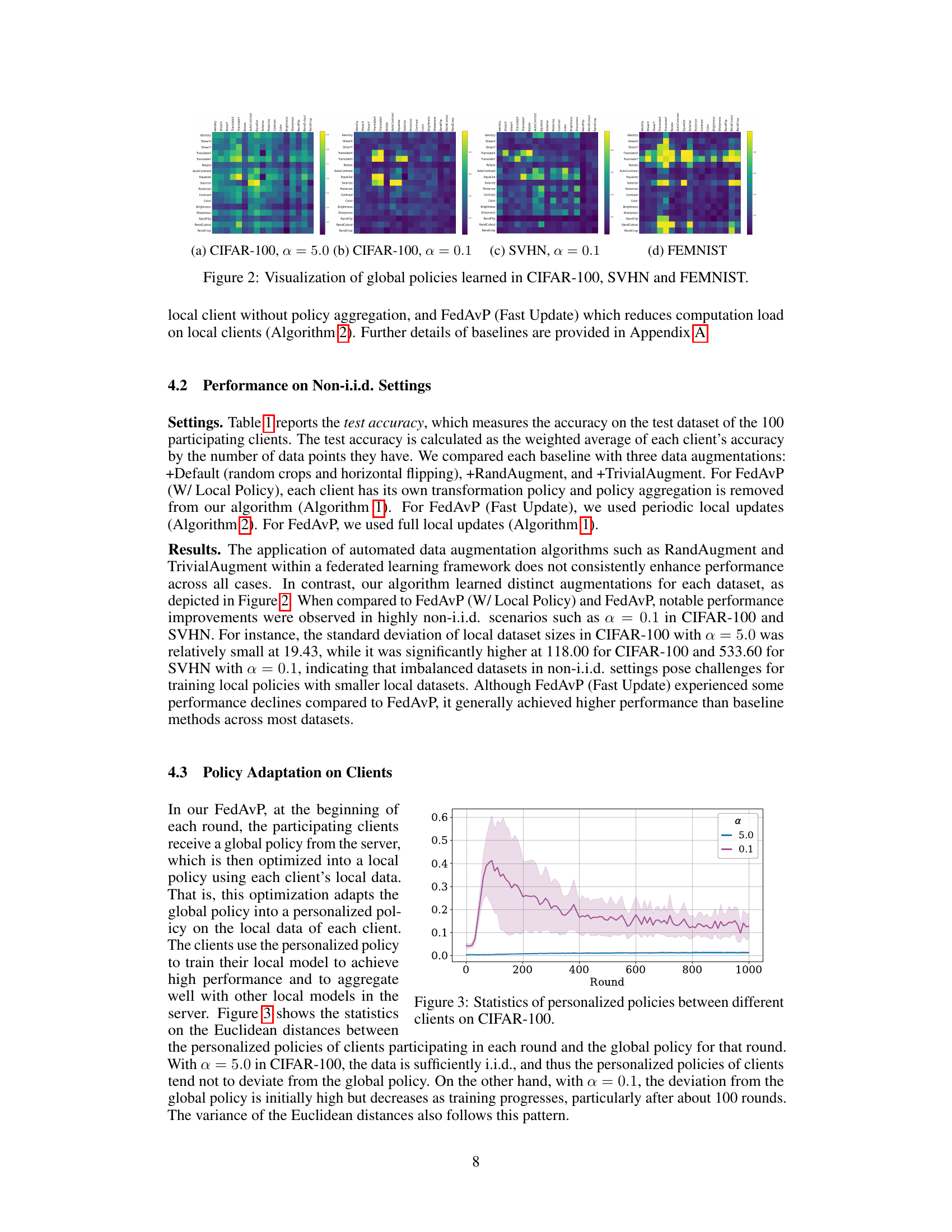
This figure visualizes the learned global data augmentation policies for CIFAR-100, SVHN, and FEMNIST datasets. Each subfigure represents a heatmap showing the probability of selecting pairs of augmentation operations. The brighter the color, the higher the probability. This visualization helps understand how the algorithm learns different augmentation strategies for different datasets.
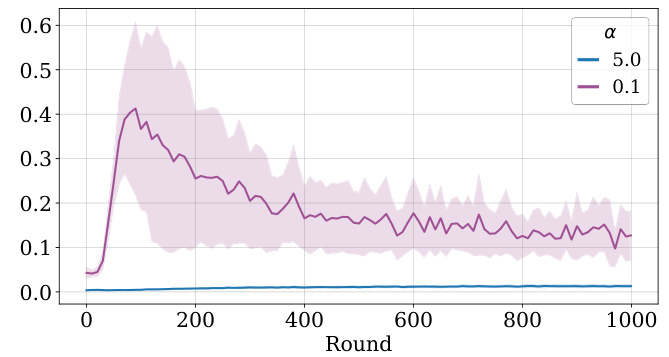
This figure shows the Euclidean distances between the personalized policies of clients participating in each round and the global policy for that round on CIFAR-100. With α = 5.0 (i.i.d. data), the personalized policies of clients tend not to deviate from the global policy. With α = 0.1 (non-i.i.d. data), the deviation from the global policy is initially high but decreases as training progresses, particularly after about 100 rounds. The variance of the Euclidean distances also follows this pattern. This illustrates how FedAvP adapts policies to heterogeneous data distributions.

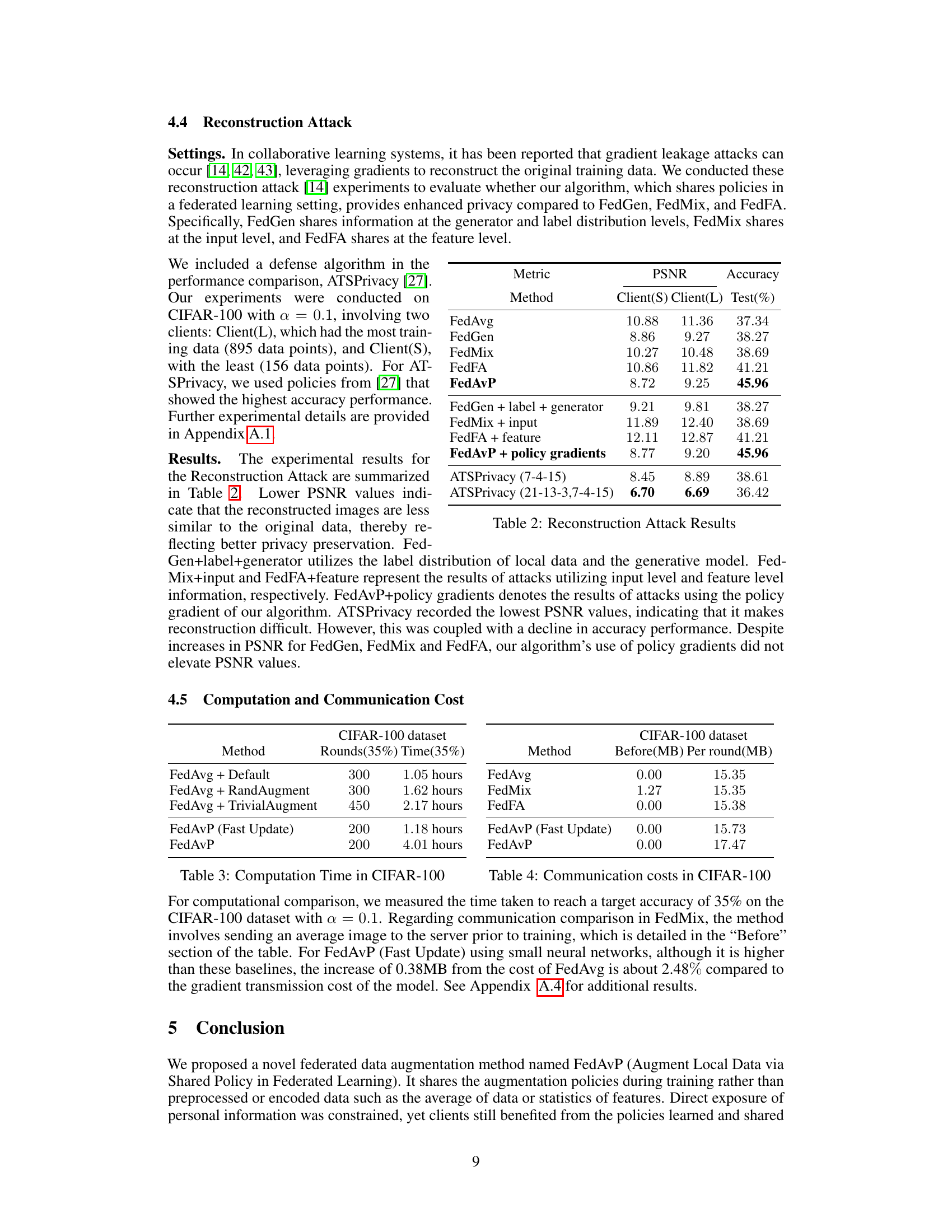
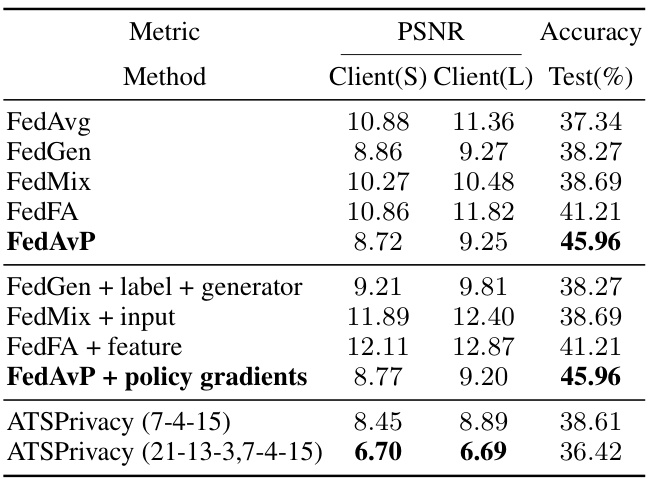
This figure shows the results of reconstruction attacks from Table 2. For each method (FedAvg, FedGen, FedMix, FedFA, FedAvP, and the defense method ATSPrivacy), it displays the original samples from a client with a small amount of data (Client(S)) and a client with a large amount of data (Client(L)), as well as the samples reconstructed by the server using the gradient information. The PSNR (Peak Signal-to-Noise Ratio) values, which represent the image quality of the reconstructed samples relative to the original samples, are also shown.

This figure visualizes the global policies learned by FedAvP for three different datasets: CIFAR-100, SVHN, and FEMNIST. Each subfigure shows a heatmap representing the probability of selecting different pairs of augmentation operations. The heatmaps reveal the distinct augmentation strategies learned for each dataset, highlighting the algorithm’s ability to adapt to heterogeneous data distributions.

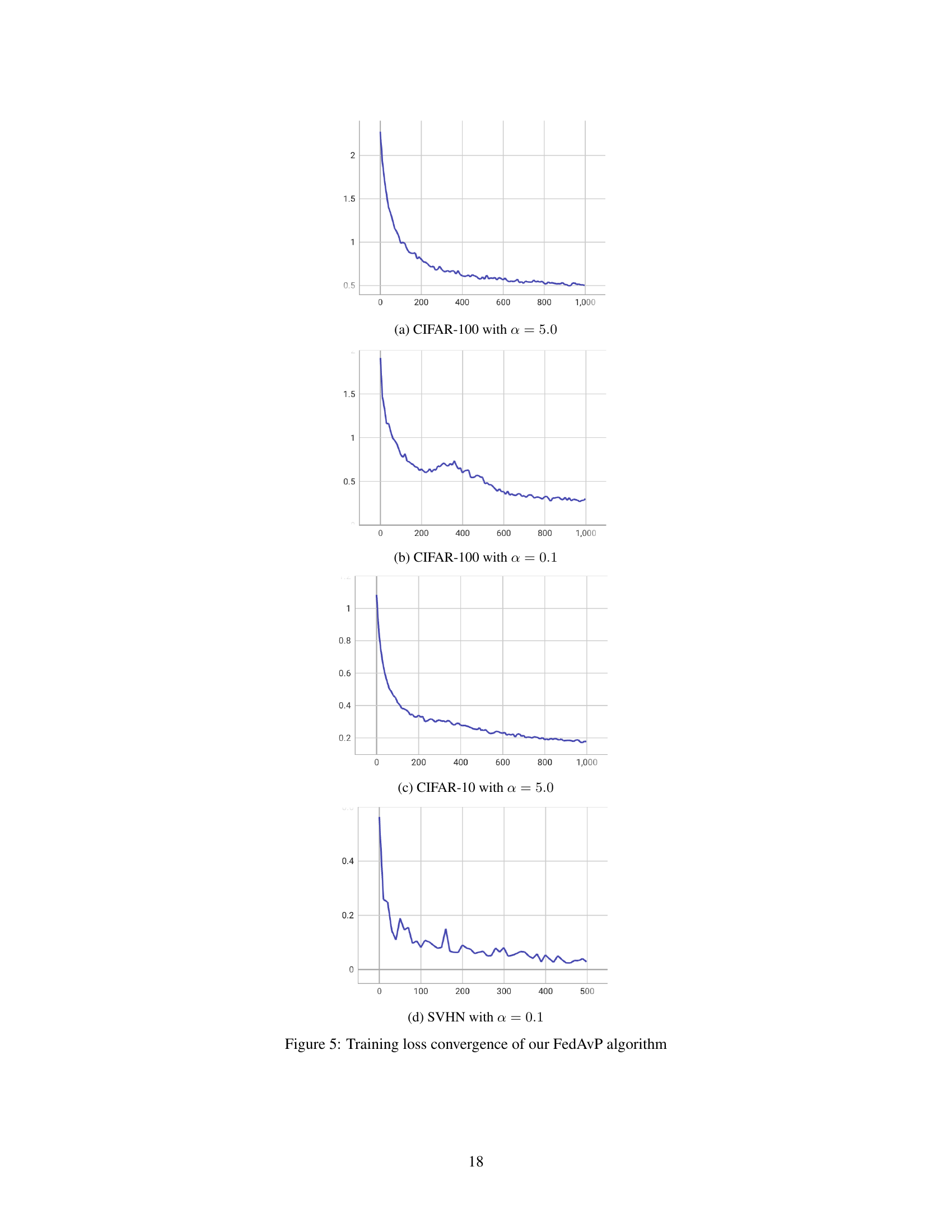
The figure shows the training loss convergence curves for the proposed FedAvP algorithm across different datasets and heterogeneity levels (alpha values). The x-axis represents the training round, and the y-axis represents the training loss. The curves illustrate how the training loss decreases over time for FedAvP, demonstrating its effectiveness in optimizing the augmentation policies for federated learning.

The figure shows the training loss curves for the FedAvP algorithm across different datasets and heterogeneity levels (alpha values). It demonstrates the convergence behavior of the algorithm’s training loss over multiple rounds, providing insight into its training dynamics and stability. The different lines represent the training loss for each dataset and heterogeneity setting.

The figure shows the training loss convergence curves for the FedAvP algorithm across four different datasets and heterogeneity levels. The x-axis represents the training round, while the y-axis shows the training loss. The plots illustrate how the training loss decreases over time for each dataset and heterogeneity setting, providing insights into the convergence behavior of the FedAvP algorithm in various scenarios.
More on tables
This table presents the test accuracy results for various federated learning algorithms across three datasets (CIFAR-100/10, SVHN, and FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The algorithms are tested with different data augmentation methods (Default, RandAugment, TrivialAugment). The table shows the test accuracy for each algorithm and augmentation method, highlighting the superior performance of FedAvP, particularly in the more heterogeneous setting (α = 0.1). The results are averages over three runs, with standard deviations provided for FedAvP (Fast Update) and FedAvP.

This table presents the classification accuracy results for various federated learning methods on three different datasets (CIFAR-100/10, SVHN, and FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The results are averaged across three random seeds, showing the mean and standard deviation for the proposed FedAvP algorithm and its Fast Update variant. The table allows a comparison of FedAvP against several baseline methods and data augmentation techniques (RandAugment and TrivialAugment), highlighting its performance in both i.i.d. and non-i.i.d. data settings.

This table presents the classification accuracies achieved by various federated learning methods on three different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under two levels of data heterogeneity (α = 5.0 and α = 0.1). The results show the performance of standard methods (FedAvg, FedProx, FedDyn, FedExP), federated data augmentation methods (FedGen, FedMix, FedFA), and the proposed method (FedAvP) with and without additional data augmentation techniques (RandAugment and TrivialAugment). Results are averaged over three runs and include standard deviations for FedAvP and its faster update variant.

This table presents the classification test accuracy results achieved by various federated learning methods across four datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under two different levels of data heterogeneity (α = 5.0 and α = 0.1). The results are averaged over three different random seeds for each method and dataset combination. For FedAvP and its fast update version, standard deviations are also included. The table shows the impact of heterogeneity on model performance, and how different data augmentation strategies impact the results of various federated learning algorithms.

This table presents the test accuracy results for various federated learning methods across different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) and heterogeneity levels (α = 5.0 and α = 0.1). The methods include standard federated learning algorithms (FedAvg, FedProx, FedDyn, FedExP) and federated data augmentation techniques (FedGen, FedMix, FedFA), each tested with and without additional data augmentation methods (RandAugment, TrivialAugment). The table shows the performance of the proposed algorithm, FedAvP, and its variants (FedAvP with Local Policy, FedAvP with Fast Update), comparing their performance to the baselines. Results are averaged across three random seeds, with standard deviations provided for FedAvP and its fast update variant.

This table presents the test accuracy results for various federated learning algorithms across four datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under different levels of data heterogeneity (represented by α = 5.0 and α = 0.1). The algorithms are evaluated with and without additional data augmentation techniques (Default, RandAugment, TrivialAugment). The table highlights the performance of the proposed FedAvP algorithm and its faster variant (FedAvP (Fast Update)) compared to various baselines, showing improvements, particularly in highly heterogeneous settings.
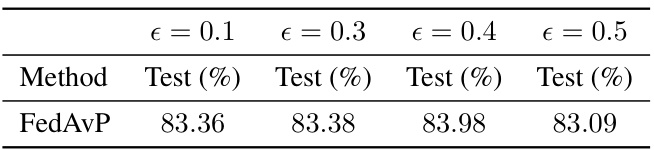
This table presents the classification test accuracy results for various federated learning algorithms on three different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under two different levels of data heterogeneity (α = 5.0 and α = 0.1). The algorithms are compared with and without different data augmentation methods (Default, RandAugment, TrivialAugment). The table shows the average test accuracy over three random seeds, and also includes standard deviations for the FedAvP (Fast Update) and FedAvP methods.
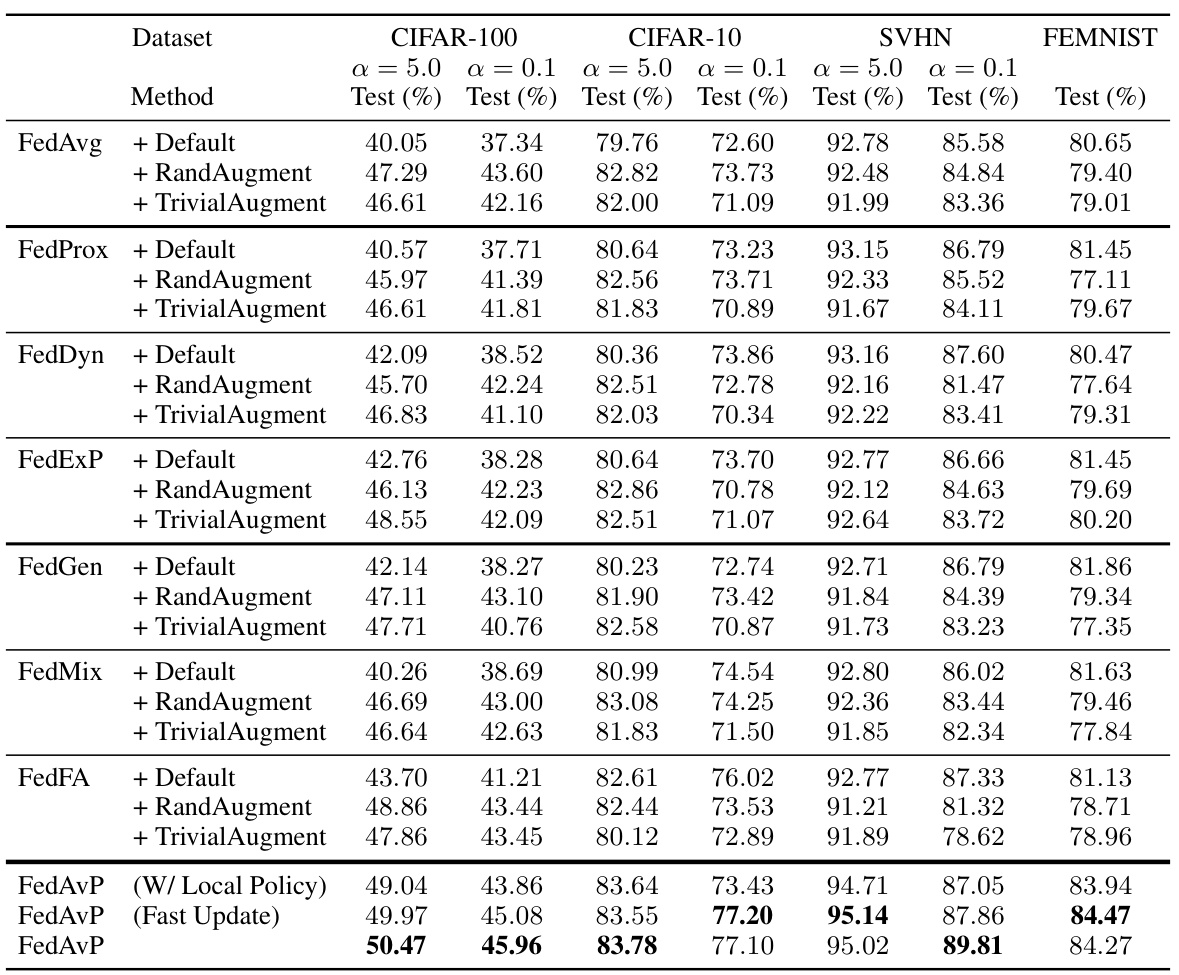
This table presents the classification accuracy results achieved by various federated learning methods (including FedAvg, FedProx, FedDyn, FedExP, FedGen, FedMix, and FedFA) on four different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST). The results are broken down by the level of data heterogeneity (α = 5.0 and α = 0.1), with each method tested using three different data augmentation techniques: default, RandAugment, and TrivialAugment. The table also includes results for the proposed FedAvP method with local policies and fast updates, showing its performance compared to the baselines.

This table presents the test accuracy results for various federated learning algorithms on three different datasets (CIFAR-100/10, SVHN, FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The algorithms are evaluated with default augmentations, RandAugment, and TrivialAugment. The results are averaged over three random seeds, and the standard deviation is shown for FedAvP and its fast update variant.

This table presents the classification accuracies achieved by various federated learning methods on three different datasets (CIFAR-100/10, SVHN, and FEMNIST) under varying degrees of data heterogeneity (α = 5.0 and α = 0.1). The results are averaged over three random seeds, providing a measure of the methods’ robustness and generalizability. The table includes baseline methods such as FedAvg, FedProx, and others, along with data augmentation techniques and the proposed FedAvP method with and without the fast update. The variance is specifically reported for the FedAvP method with and without the fast update, highlighting their performance consistency.

This table presents the classification accuracy results for various federated learning algorithms on three benchmark datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST). It compares the performance of standard algorithms (FedAvg, FedProx, FedDyn, FedExP) with and without data augmentation techniques (RandAugment and TrivialAugment), and also against existing federated data augmentation methods (FedGen, FedMix, FedFA). The key comparison is against the proposed FedAvP algorithm, which is tested with and without a fast update optimization. Results are reported for two levels of data heterogeneity (α=5.0 and α=0.1), showing the robustness and effectiveness of FedAvP under different non-i.i.d. settings. Error bars are provided for FedAvP to show statistical significance.

This table presents the test accuracy results for various federated learning algorithms on three benchmark datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under two different levels of data heterogeneity (α = 5.0 and α = 0.1). The algorithms are evaluated with and without data augmentation techniques (Default, RandAugment, TrivialAugment). The results are averaged over three random seeds and show the performance of FedAvP compared to other methods, along with statistical variance for FedAvP and its fast update version.
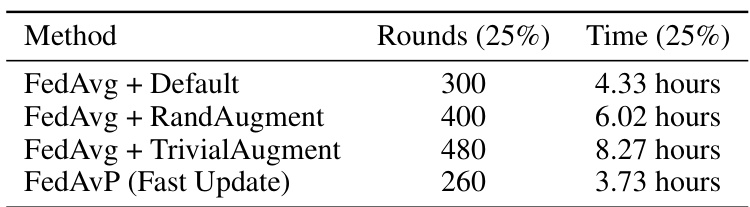
This table presents the classification accuracies achieved by different federated learning methods on various datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under two different levels of data heterogeneity (α = 5.0 and α = 0.1). The results include baselines (FedAvg, FedProx, FedDyn, FedExP, FedGen, FedMix, FedFA) with and without data augmentation techniques (Default, RandAugment, TrivialAugment). The performance of the proposed FedAvP method is shown, along with a variant using a fast update strategy and a comparison to a local policy approach. Results are averages across three random seeds, and standard deviations are provided for FedAvP and its fast update version.
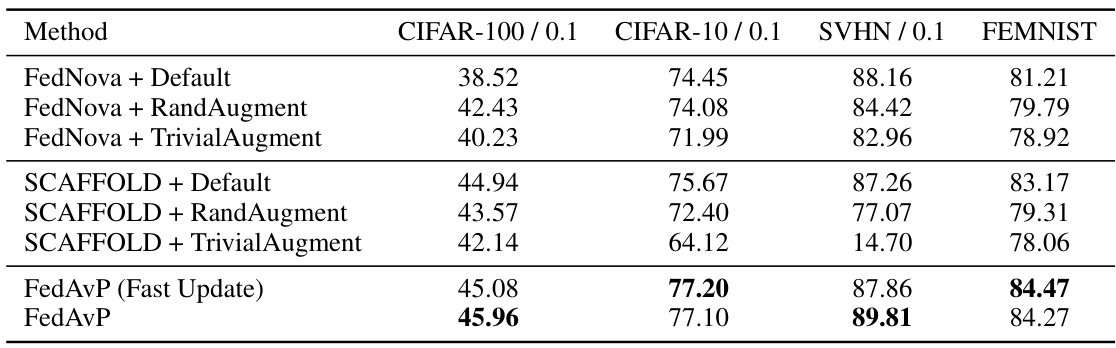
This table presents the classification accuracy results for various federated learning methods across different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The methods tested include FedAvg, FedProx, FedDyn, FedExP, FedGen, FedMix, and FedFA, each combined with default augmentations, RandAugment, and TrivialAugment. The table also includes results for FedAvP (with local policy search), FedAvP (Fast Update), and the proposed FedAvP method. Results are averaged over three random seeds, with standard deviations reported for FedAvP and FedAvP (Fast Update) to show the consistency and stability of the results.
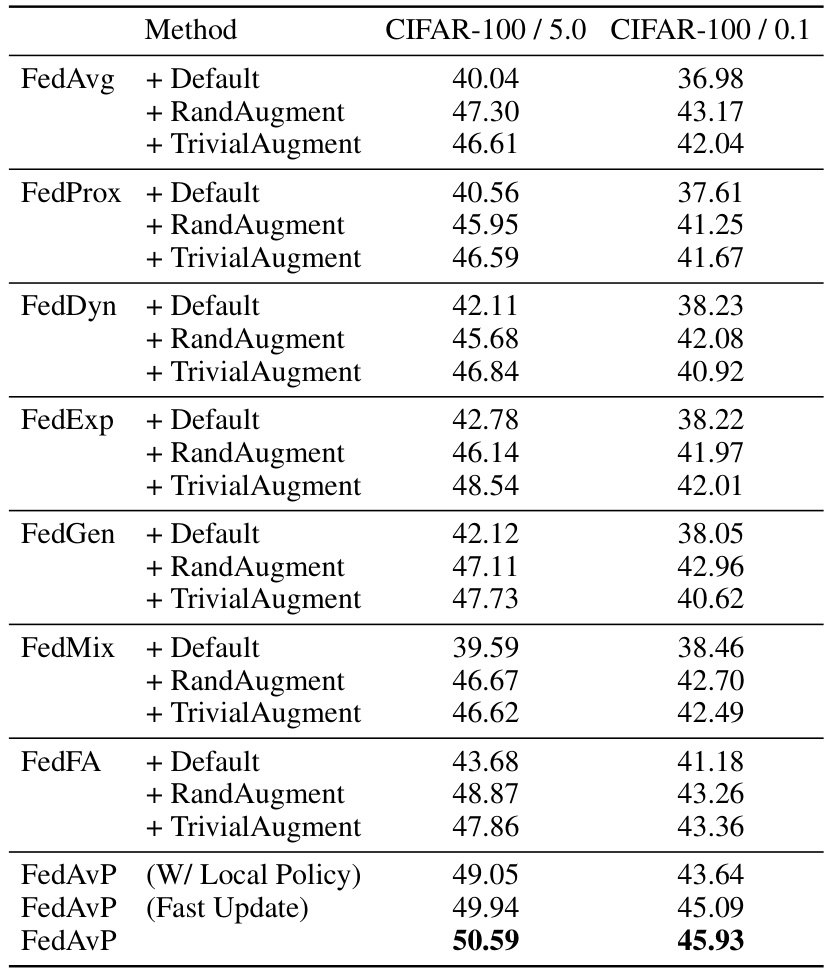
This table presents the classification accuracies achieved by various federated learning methods (FedAvg, FedProx, FedDyn, FedExP, FedGen, FedMix, FedFA, and FedAvP) on three different datasets (CIFAR-100, CIFAR-10, SVHN, and FEMNIST) under different levels of data heterogeneity (α = 5.0 and α = 0.1). The results are averaged over three independent runs, and standard deviations are reported for FedAvP (Fast Update) and FedAvP to show the consistency of the results. The table allows comparison of the proposed method (FedAvP) with existing methods, both standard federated learning algorithms and federated data augmentation techniques, under varying data distributions.

This table presents the classification accuracy results for various federated learning algorithms on three different datasets (CIFAR-100/10, SVHN, and FEMNIST) under two different levels of data heterogeneity (α = 5.0 and α = 0.1). Each algorithm is tested with three data augmentation methods: Default, RandAugment, and TrivialAugment. The table shows that the proposed FedAvP algorithm outperforms existing methods, especially in the high heterogeneity setting (α = 0.1). Results are averaged across three random seeds, and variances are provided for FedAvP and its Fast Update variant.
Full paper#