GLinSAT: The General Linear Satisfiability Neural Network Layer By Accelerated Gradient Descent

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is highly important for researchers working on constrained optimization problems, neural network architectures, and differentiable programming. It offers a novel and efficient solution to a common challenge in applying neural networks to real-world problems, bridging the gap between neural networks and optimization solvers. The proposed method’s general applicability and improved efficiency make it valuable for various domains. Furthermore, it opens new avenues for research into efficient and differentiable constrained optimization layers.

Visual Insights

#

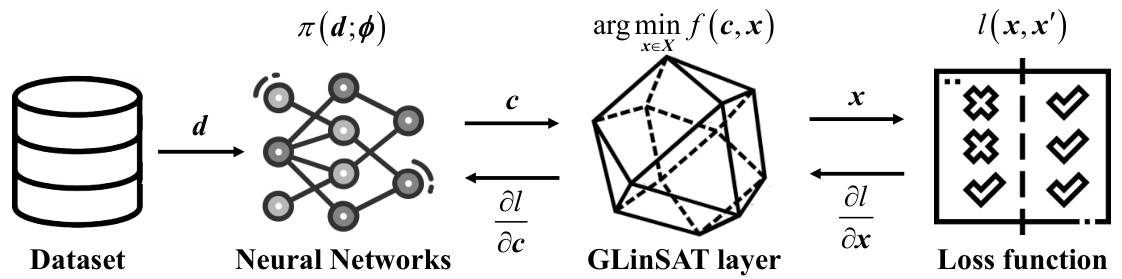
The figure shows a pipeline illustrating the workflow of the GLinSAT layer. It starts with a dataset (d) which is processed by a neural network to produce outputs (c). These outputs (c) are then passed through the GLinSAT layer, which projects the outputs onto a feasible region defined by constraints (represented by the polyhedron). The resulting feasible outputs (x) are then used to calculate a loss, which is used in the training process to optimize the network parameters. The dashed lines represent the flow of gradients used for optimization during backpropagation.

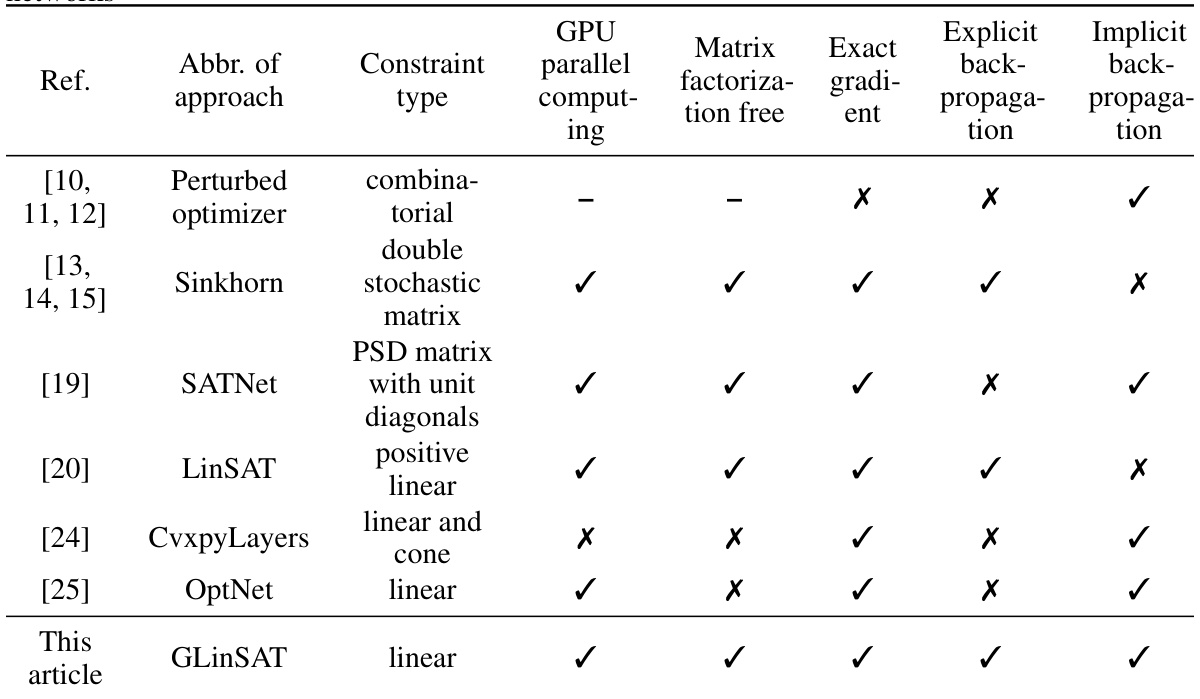
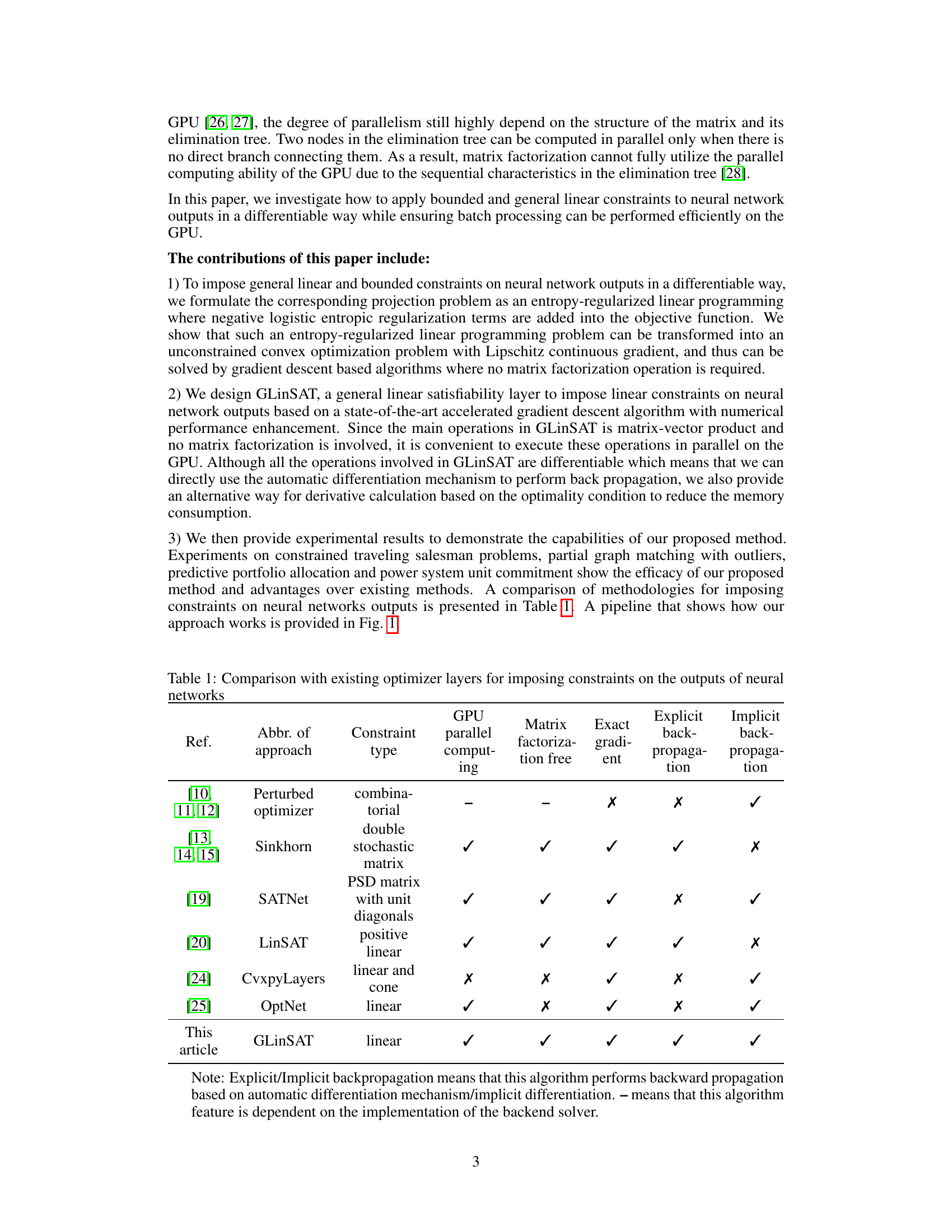
This table compares GLinSAT with other state-of-the-art methods for imposing constraints on neural network outputs. It contrasts the constraint type handled, GPU parallel computing capabilities, whether matrix factorization is needed, if exact gradients are available, and whether explicit or implicit backpropagation is used.

In-depth insights

#

GLinSAT: A Deep Dive

#

GLinSAT, as a novel neural network layer, presents a significant advancement in handling general linear constraints within neural network outputs. Its core innovation lies in efficiently reformulating the constrained optimization problem into an unconstrained convex optimization problem, leveraging the power of accelerated gradient descent. This method bypasses the computational bottlenecks often associated with matrix factorization, making it significantly faster and more memory-efficient than existing approaches. The differentiability of all operations in GLinSAT ensures seamless integration within standard backpropagation, allowing for end-to-end training and improved accuracy. Furthermore, the use of an advanced accelerated gradient descent algorithm with numerical performance enhancements enhances the efficiency and stability of the solution process. The paper’s experimental results across various constrained optimization problems—including the traveling salesman problem and power system unit commitment—demonstrate GLinSAT’s clear advantages in terms of speed, memory efficiency, and solution quality. However, future research should explore its limitations with non-linear constraints and scalability to even larger-scale problems.

Linear Constraint Layer

#

A linear constraint layer in a neural network is a module that enforces linear constraints on the network’s outputs. This is crucial for many real-world applications where the model’s predictions must satisfy specific conditions, such as resource limitations, physical boundaries, or regulatory requirements. The core challenge lies in seamlessly integrating constraint satisfaction with the differentiability needed for backpropagation. Various methods exist, ranging from penalty methods (adding penalty terms to the loss function for violations) to methods that directly solve optimization problems within the layer. Penalty methods are simpler to implement but may not guarantee constraint satisfaction, while direct solvers offer strong guarantees but are computationally more expensive. Accelerated gradient descent algorithms can significantly improve the efficiency of direct solvers. The choice of method often involves a trade-off between computational cost and the strictness of constraint adherence. An ideal linear constraint layer would be both efficient and guarantee constraint satisfaction, ideally through a differentiable process compatible with various neural network architectures. Future research will likely focus on improving the efficiency and scalability of these layers for increasingly complex constraint scenarios.

Accelerated Gradient

#

Accelerated gradient methods are crucial for optimizing the performance of machine learning models, particularly deep neural networks. They address the limitations of standard gradient descent, which can be slow to converge, especially in high-dimensional spaces. The core idea behind acceleration is to incorporate information from previous gradient steps to better predict the direction of the optimal solution. This often involves cleverly combining gradients from multiple iterations, often using momentum or similar techniques. The benefit of accelerated methods is a significant reduction in training time and computational resources, allowing for the training of larger and more complex models. However, the choice of acceleration technique is critical and depends heavily on the specific problem and dataset. Poorly chosen hyperparameters can lead to instability or even divergence, negating any performance gains. Further research is focused on developing more robust and adaptive acceleration methods that automatically adjust to the characteristics of the learning process and that can handle increasingly complex model architectures and datasets more efficiently. The effectiveness of any accelerated gradient method is dependent on factors like learning rate, batch size, and the choice of optimizer, highlighting the need for careful experimentation and fine-tuning.

Experimental Results

#

The ‘Experimental Results’ section is crucial for validating the claims of the GLinSAT neural network layer. The authors wisely chose diverse and challenging problems to showcase GLinSAT’s capabilities. Constrained Traveling Salesman Problem (TSP), Partial Graph Matching with Outliers, Predictive Portfolio Allocation, and Power System Unit Commitment are all representative of real-world constrained optimization scenarios. The comparison against existing methods like LinSAT, CvxpyLayers, and OptNet provides a robust benchmark. GLinSAT’s consistently superior performance across these diverse tasks, particularly its efficiency gains on GPUs, highlights its effectiveness and scalability. However, a thoughtful discussion of limitations, such as the computational cost for exceptionally large-scale problems or the current constraint type limitations (only linear), would strengthen this section, providing a more balanced assessment of the proposed method’s practical implications.

Future Directions

#

Future research could explore extending GLinSAT to handle more complex constraint types beyond general linear constraints, such as conic constraints or integer constraints. Improving the efficiency of the backward pass is crucial, perhaps through more advanced derivative calculation techniques or specialized hardware acceleration. Investigating the theoretical properties of GLinSAT, such as convergence rates under different conditions, would strengthen its foundation. Applications to large-scale real-world problems, like those in logistics, finance, or energy, would showcase its practical impact and further highlight its advantages over existing methods. Finally, developing a more user-friendly interface and integrating GLinSAT into existing deep learning frameworks would make it more accessible to a wider range of researchers and practitioners.

More visual insights

#

More on tables

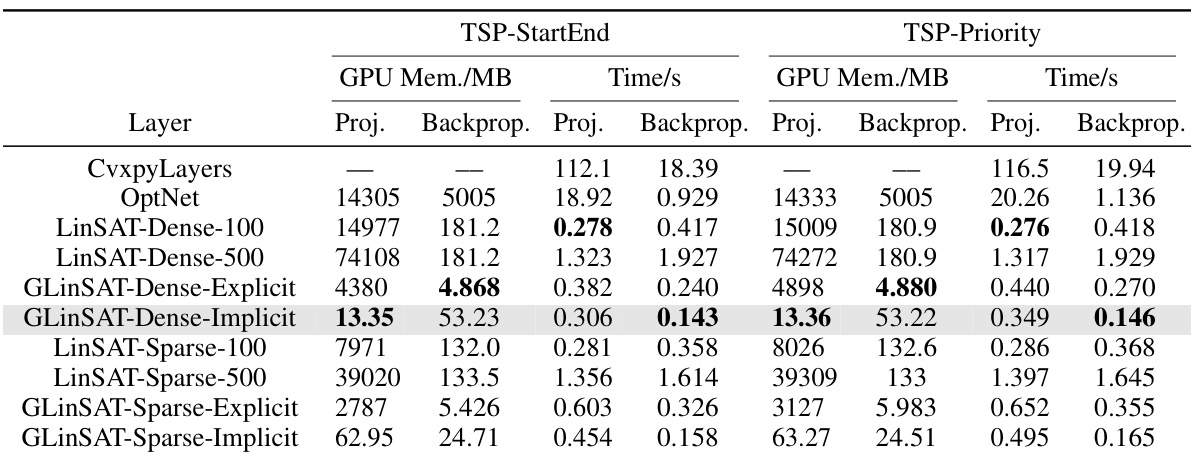
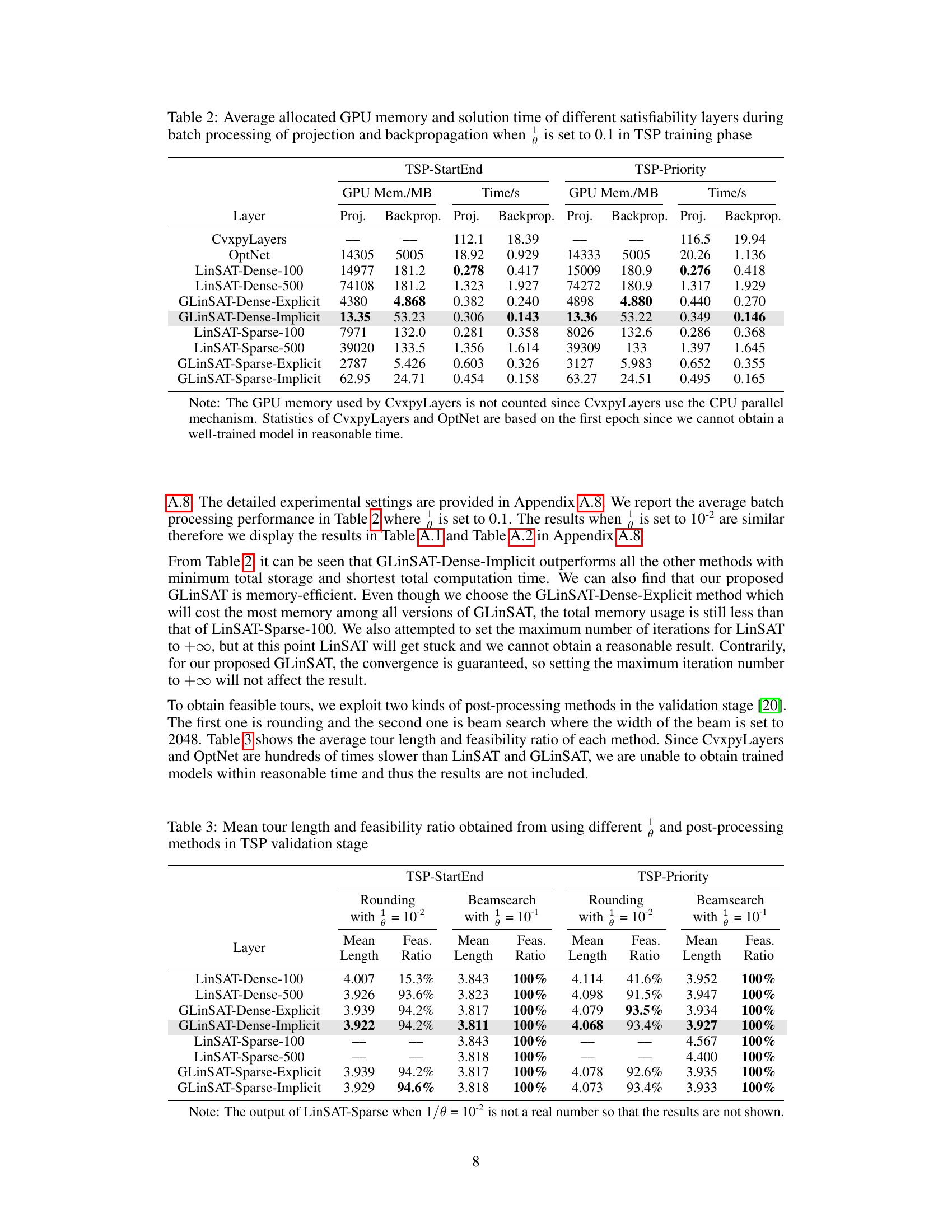
This table compares the GPU memory usage and computation time of various satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) during the training phase of solving Traveling Salesperson Problems (TSP). It shows the performance difference for both projection and backpropagation, separating dense and sparse matrix implementations of LinSAT and GLinSAT. The results are broken down by the type of backpropagation used (explicit or implicit) and indicate the impact of different approaches on computational efficiency and memory requirements.

This table shows a comparison of the GPU memory and time used for projection and backpropagation by different satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) when training on the Traveling Salesman Problem (TSP) with two types of constraints: TSP with start and end city constraints and TSP with priority constraints. The results are shown separately for the projection and backpropagation phases of each layer, providing a comprehensive view of their computational efficiency. The table also shows how the different implementations of GLinSAT (dense/sparse, explicit/implicit) perform.

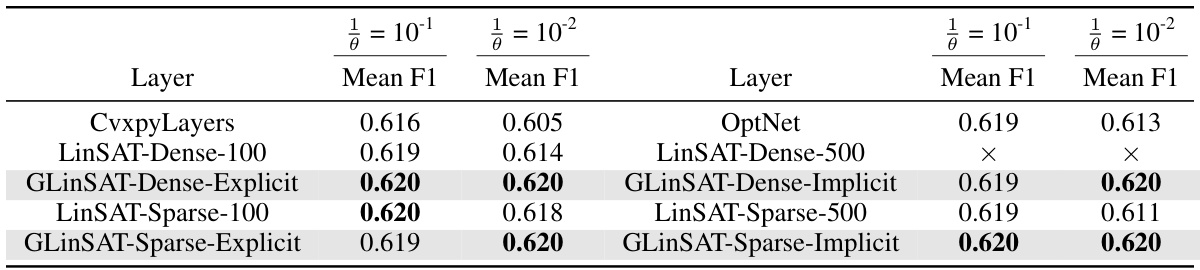
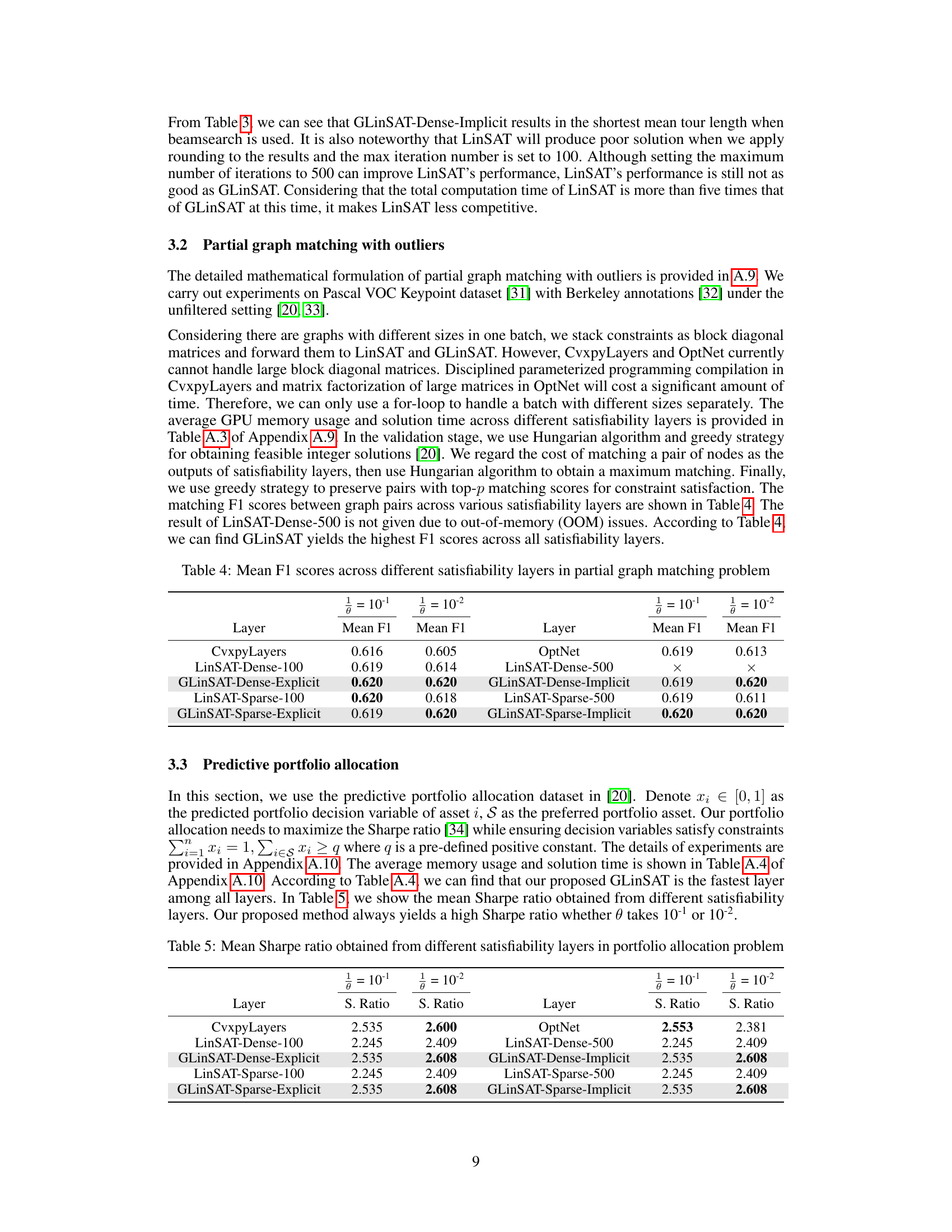
This table presents the mean F1 scores achieved by different satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) on a partial graph matching problem. The results are broken down by the inverse temperature parameter (θ) used in the entropy-regularized linear programming formulation. The table allows for a comparison of the performance of different methods for imposing linear constraints in a neural network context.

This table compares the GPU memory usage and the time spent on projection and backpropagation for different satisfiability layers (CvxpyLayers, OptNet, LinSAT, GLinSAT) when solving the Traveling Salesman Problem (TSP). It shows the performance for two variations of the TSP: TSP with starting and ending cities constraints, and TSP with priority constraints. The results are broken down by whether a dense or sparse matrix representation was used, and whether explicit or implicit backpropagation was used in GLinSAT. The table highlights the efficiency gains of GLinSAT, especially the implicit version, in terms of both memory usage and computation time.

This table shows the feasibility ratio and average gap obtained from using different values of the inverse temperature parameter (1/θ) in the validation stage of the power system unit commitment experiment. It compares results obtained by using the proposed GLinSAT-Sparse-Implicit method with a sigmoid activation function, showing how the feasibility of solutions increases as 1/θ approaches 0. The table also includes results using Gurobi-LP, which solves the linear programming problem with the integer unit commitment variables fixed, to compare performance with GLinSAT.

This table compares the GPU memory usage and computation time of various satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) during the training phase of solving Traveling Salesperson Problems (TSPs) with two different types of constraints: TSP with start and end city constraints, and TSP with priority constraints. The results show GLinSAT’s efficiency compared to other methods in terms of memory and processing speed for both types of constraints, especially when using implicit backpropagation.

This table presents the results of experiments on the Traveling Salesman Problem (TSP) with two types of constraints (TSP-StartEnd and TSP-Priority). The table compares the performance of different satisfiability layers (LinSAT and GLinSAT variants) in terms of mean tour length and feasibility ratio, after applying two different post-processing techniques: rounding and beam search. The results are shown for different values of the regularization parameter (θ).

This table shows the GPU memory usage and the time spent on projection and backpropagation for different satisfiability layers when solving the Traveling Salesman Problem (TSP). It compares the performance of GLinSAT against other methods such as CvxpyLayers, OptNet, and LinSAT, considering both dense and sparse matrix implementations and explicit/implicit backpropagation. The results are broken down by the type of TSP constraint (TSP-StartEnd and TSP-Priority).

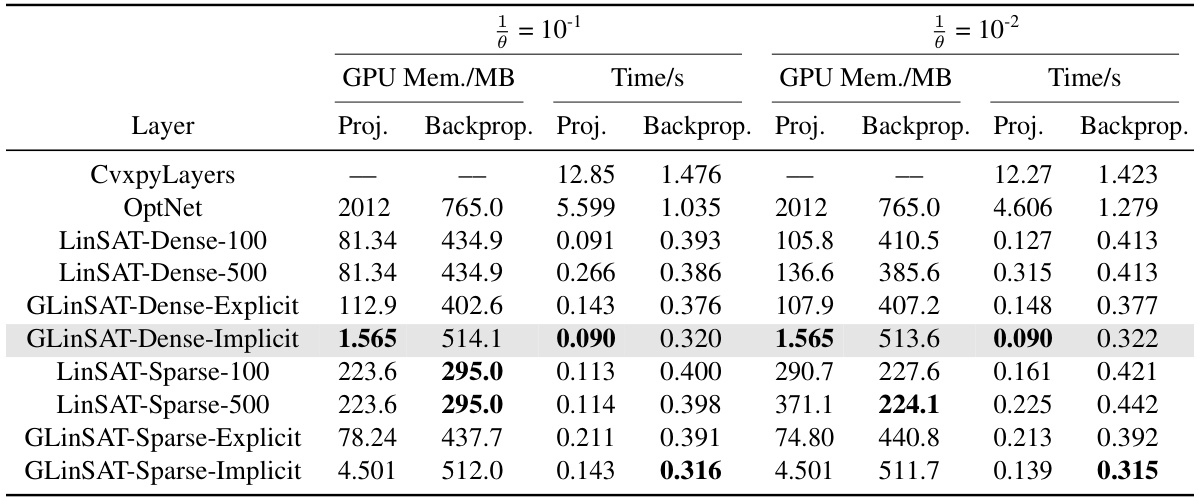
This table compares the GPU memory usage and computation time for projection and backpropagation steps of various satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) on two versions of the Traveling Salesperson Problem (TSP). It shows the performance differences across dense and sparse matrix implementations, and explicit vs. implicit backpropagation methods. The results highlight the efficiency gains of GLinSAT, especially in the implicit backpropagation approach.

This table compares the GPU memory usage and computation time of various satisfiability layers (CvxpyLayers, OptNet, LinSAT, and GLinSAT) during the training phase of a Traveling Salesperson Problem (TSP). It shows the memory used for projection and backpropagation separately, as well as the time taken for each. The results are broken down by the specific satisfiability layer used and whether a dense or sparse matrix representation was used, and whether explicit or implicit backpropagation was utilized. The purpose is to demonstrate the efficiency of GLinSAT in comparison to other methods.

Full paper

#