↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Causal disentanglement aims to uncover latent causal factors from data, improving model interpretability and extrapolative power. Existing methods often assume interventional data, which is often unrealistic for latent variables. This limits their applicability and raises the question of what can be learned using only observational data. This limitation has hampered progress and the development of techniques applicable to broader real-world scenarios.
This research tackles the challenge by focusing on nonlinear causal models with additive Gaussian noise and linear mixing. The study provides theoretical guarantees for identifiability of latent factors up to a layer-wise transformation. This is a significant improvement, as it means we can extract valuable causal information even without manipulating the system. Furthermore, they present a novel practical algorithm that solves a quadratic program for score estimation, enabling researchers to derive meaningful causal representations directly from observational data. The algorithm’s efficiency and flexibility is highlighted by simulations.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in causal inference and representation learning. It offers novel identifiability guarantees for causal disentanglement using only observational data, a significant advancement in the field. The proposed algorithm is practical and opens new avenues for research, particularly in applications where interventional data is scarce or impossible to obtain.
Visual Insights#
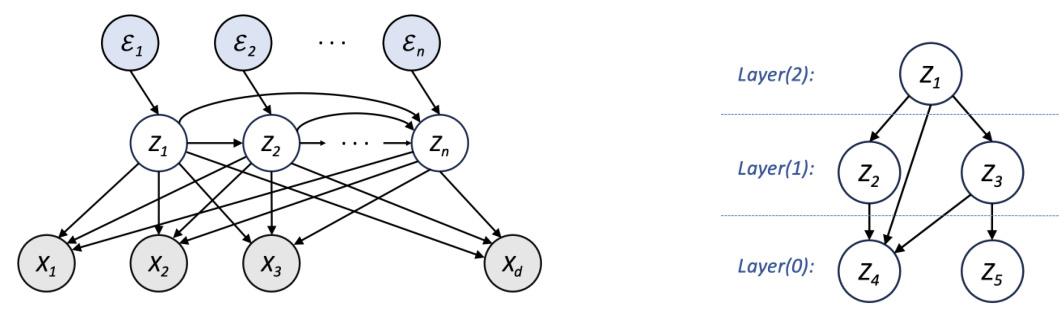
The figure illustrates the data generating process described in the paper. It shows how latent variables Z are generated by a nonlinear causal model with additive Gaussian noise. These latent variables are then linearly mixed to produce the observed variables X. The arrows represent causal relationships, with the direction indicating the influence of one variable on another. The figure shows that multiple latent variables can influence the same observed variable (and vice versa), and demonstrates the process of disentanglement that aims to extract individual causal factors from the mixed observational data.
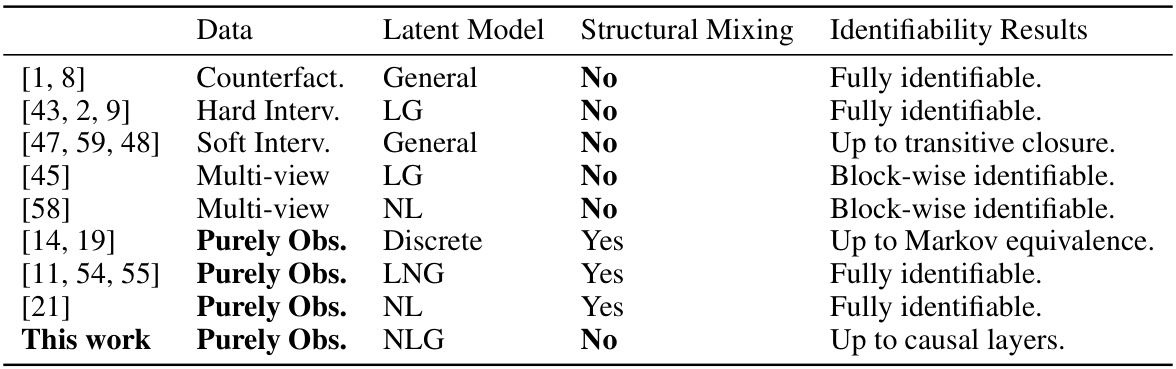
This table compares the identifiability results of the proposed method with those of existing methods in causal disentanglement. The comparison is based on several factors: the type of data used (counterfactual, interventional, or purely observational), the type of latent model (linear or nonlinear), the nature of the mixing function between latent and observed variables (linear or nonlinear), and the achieved level of identifiability. The identifiability results are described in terms of the ability to fully identify the latent causal graph, identify it up to a specific equivalence class (e.g., Markov equivalence), or identify only blocks of the graph.
In-depth insights#
Causal ID. Limits#
The heading ‘Causal ID. Limits’ suggests an exploration of the boundaries and constraints inherent in causal identification. A thoughtful analysis would delve into the inherent challenges of establishing causality, particularly when dealing with complex systems and limited data. Identifying causal relationships often relies on assumptions that may not hold true in real-world scenarios, such as the absence of confounding variables or the presence of linear relationships. The discussion might explore the impact of different causal modeling techniques and their respective strengths and weaknesses in handling non-linearity and high dimensionality. A core aspect would likely be the examination of identifiability, the possibility of uniquely determining causal relationships from observational data. The limitations imposed by data sparsity, measurement error, and model misspecification would also be central to understanding the limits of causal identification. Ultimately, ‘Causal ID. Limits’ would likely present a balanced perspective, acknowledging the significant progress in causal inference while emphasizing the crucial need for caution and awareness of inherent uncertainties when drawing causal conclusions.
Nonlinear Models#
Nonlinear models are crucial in various fields for accurately capturing complex relationships that cannot be adequately represented by linear models. Their ability to model intricate interactions and non-proportional effects makes them especially powerful in scenarios with high dimensionality and complex dependencies. However, the increased complexity introduces challenges in terms of interpretability, identifiability, and computational cost. Parameter estimation in nonlinear models often involves iterative methods that are sensitive to starting points and may converge to local optima. This necessitates careful consideration of regularization techniques and model selection strategies to ensure robustness and generalizability. Furthermore, identifying causal relationships within nonlinear models is significantly more challenging than in linear models, often requiring strong assumptions or specialized techniques to disentangle cause-and-effect. Despite these complexities, the potential for uncovering deeper insights and building more accurate predictive models motivates ongoing research into developing new methods and enhancing existing approaches for working effectively with nonlinear models.
Score Matching#
Score matching, in the context of causal discovery, is a powerful technique for learning causal relationships from observational data. It leverages the score function, which is the gradient of the log-likelihood of the observed data, to estimate the underlying causal structure. By analyzing the properties of the score function’s Jacobian matrix, particularly its diagonal elements and variances, we can infer the causal directionality between latent variables. This is particularly useful when we lack interventional data, as it allows us to utilize purely observational data. Nonlinear additive noise models are often employed because they effectively capture real-world causal relationships and their inherent asymmetries. This approach has significant advantages because it avoids strong assumptions, such as parametric model specifications or graphical restrictions. However, score matching methods are computationally demanding due to the requirement of estimating the second-order derivatives of the log-likelihood. Further research is needed to improve the efficiency of score matching algorithms for high-dimensional datasets. Despite these computational challenges, score matching offers a promising path toward advancing the field of causal discovery and causal representation learning.
Layerwise ID.#
The concept of “Layerwise ID.” in the context of causal disentanglement suggests a hierarchical approach to identifying latent causal factors. It implies that latent variables are not all equally identifiable; instead, identifiability is structured in layers. Root nodes, or variables without parents in the causal graph, are most easily identifiable, potentially up to a linear transformation. As one moves down the causal hierarchy, identifiability becomes more constrained, with lower layers being less precisely determined due to the increased influence of confounding factors from upstream layers. This layerwise identification approach is particularly useful when interventions are unavailable, because it leverages the inherent asymmetries in the data distribution stemming from the causal relationships between variables to infer causal directions, offering a path towards disentangling causal factors from purely observational data. A crucial aspect is the ability to recover layer-wise representations, which, while not fully disentangled, offers significant improvements in interpretability and potentially enhances extrapolation capabilities compared to traditional methods.
Future Research#
Future research directions stemming from this work could explore extending the identifiability results to more general causal models, moving beyond additive Gaussian noise and linear mixing. Investigating nonlinear mixing functions and non-Gaussian noise distributions would significantly broaden the applicability of the theoretical framework. Developing more efficient and robust algorithms for score estimation and quadratic program solving is crucial for practical implementation, particularly when dealing with high-dimensional data or limited samples. Further research could also focus on incorporating prior knowledge or additional data sources (e.g., interventions, multiple views) to enhance identifiability and disentanglement. Finally, exploring the relationships between causal disentanglement and other representation learning techniques would offer valuable insights into the strengths and limitations of each approach and may reveal synergies for future advances in causal inference.
More visual insights#
More on figures
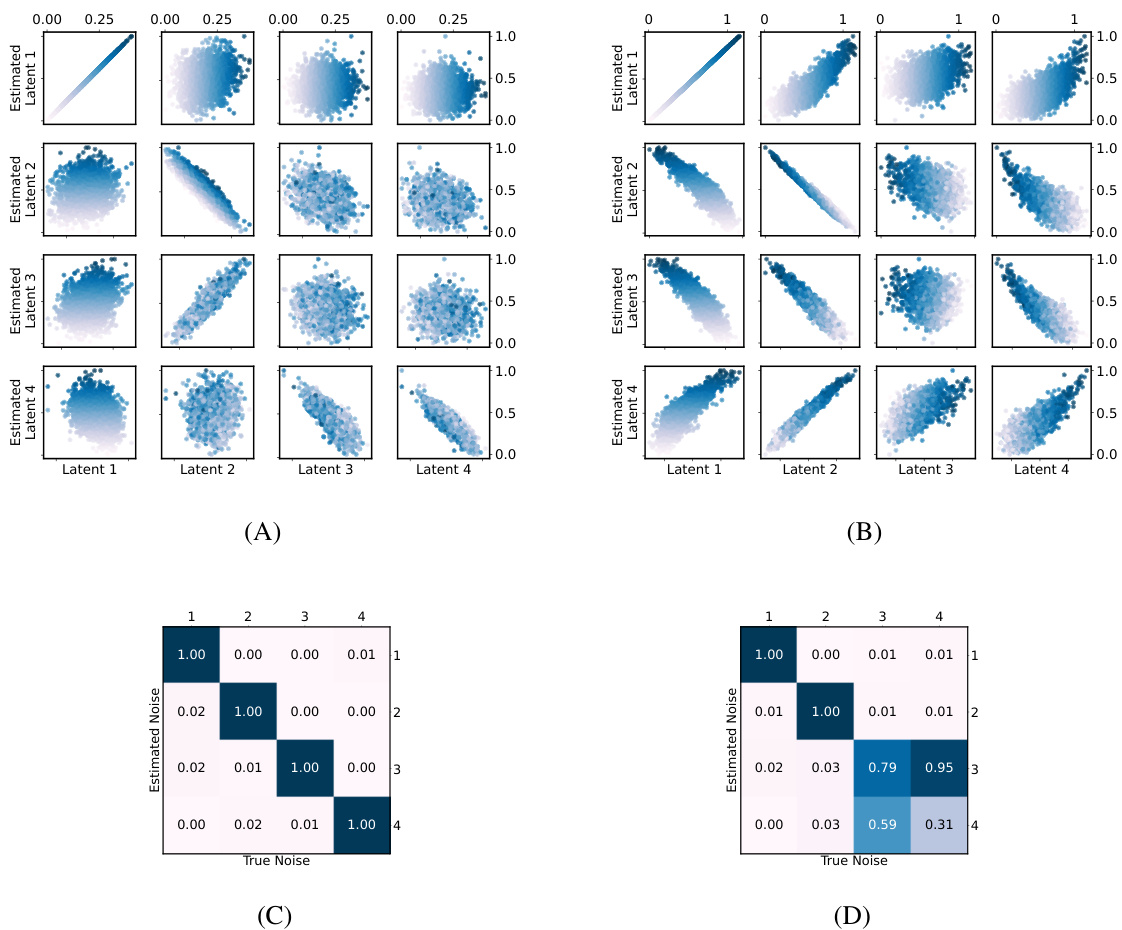
This figure shows the results of applying the proposed algorithms to simulated data with perfect score oracles. Panels (A) and (B) display scatter plots comparing the estimated latent variables to their true values for a linear causal graph and a Y-shaped causal graph, respectively. The color coding helps visualize the relationships between the variables. Panels (C) and (D) present heatmaps showing the mean absolute correlations (MAC) between the estimated and true exogenous noise variables for both graph structures, illustrating the accuracy of disentanglement.

This figure displays the results of simulations using perfect score oracles. It shows the relationship between the estimated and true latent variables for both line and Y-structure causal graphs. Scatter plots visualize the relationships between estimated and true latent variables, while heatmaps show the mean absolute correlations between estimated and true exogenous noise variables. The results demonstrate the algorithm’s ability to accurately recover latent variables, particularly for root nodes in the causal graphs.
Full paper#



















