TL;DR#
Many real-world problems involve estimating properties of expensive black-box functions, often requiring the use of computationally intensive base algorithms. Existing Bayesian Algorithm Execution (BAX) methods, like INFO-BAX, often rely on expected information gain (EIG), which can be computationally expensive and limit their applicability. This is especially true when the property of interest is complex or high-dimensional.
This paper introduces PS-BAX, a new BAX method using posterior sampling. PS-BAX is significantly faster than EIG-based approaches because it only requires a single base algorithm execution per iteration. It is also simpler to implement and easily parallelizable. Experiments across diverse tasks demonstrate that PS-BAX performs competitively with existing baselines. Furthermore, the paper provides theoretical analysis showing that PS-BAX is asymptotically convergent under mild conditions.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a faster, simpler, and easily parallelizable alternative to existing Bayesian algorithm execution methods. Its novel approach based on posterior sampling unlocks new applications and provides new theoretical insights, opening avenues for future research in algorithm design and optimization.
Visual Insights#
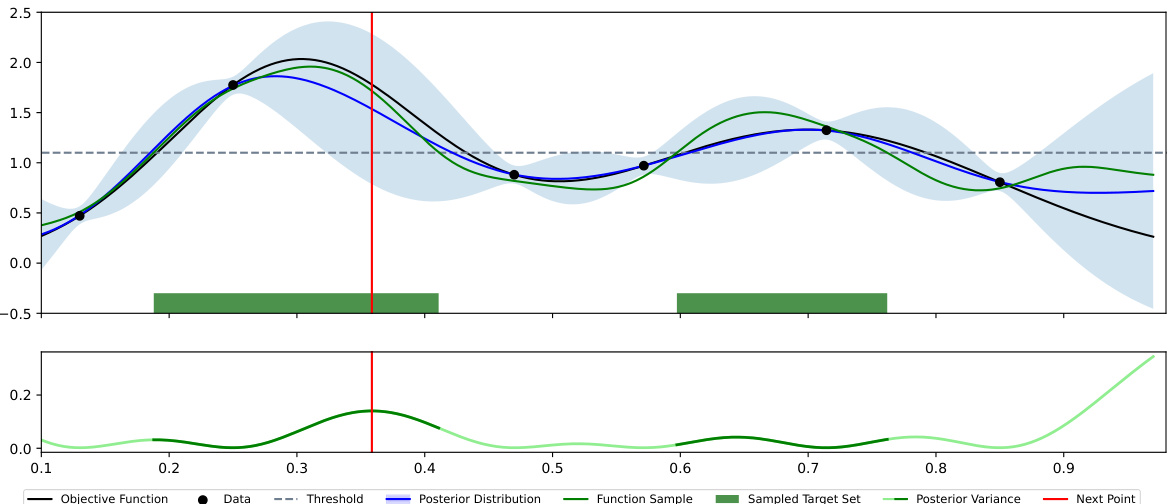
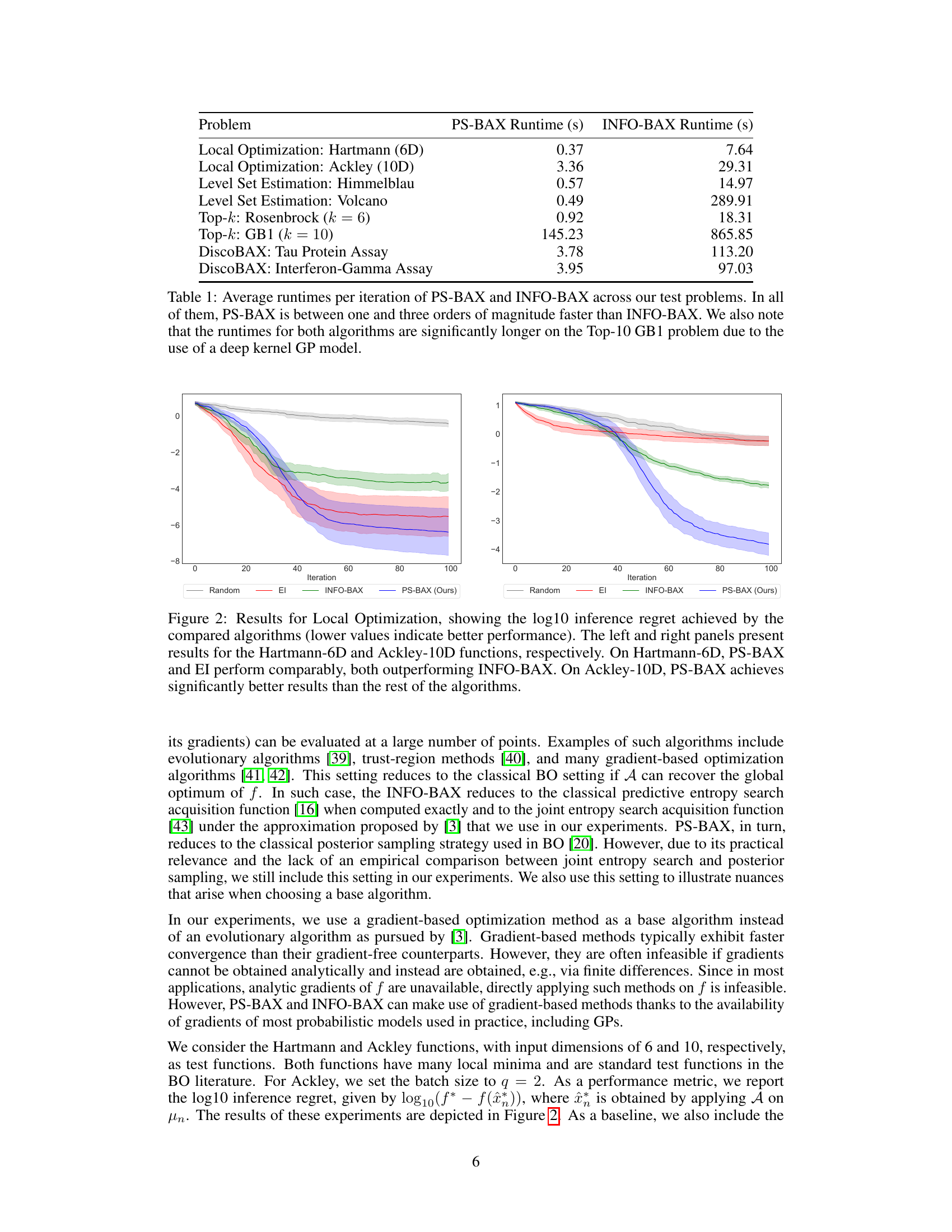
🔼 This figure illustrates one iteration of the PS-BAX algorithm for level-set estimation. It shows the true objective function, the currently observed data points, the threshold defining the level set, the posterior distribution over the function, a sample from that posterior, and the resulting target set identified from that sample. The algorithm then selects the next point to evaluate based on the uncertainty (variance) of the posterior in the sampled target set.
read the caption
Figure 1: Depiction of PS-BAX (Algorithm 1) for the level-set estimation problem. We plot the objective function f (black line), the current available data Dn−1 (black points), the threshold (grey dashed line), the posterior distribution p(f | Dn−1) (blue line and light blue region), a sample from the posterior fn ~ p(f | Dn−1) (green line), the corresponding sampled target set Xn = OA(fn) (green region) (this is the set of inputs where the green line is above the threshold), the variance of p(f | Dn−1) (green line, bottom row), and the next point to evaluate selected by PS-BAX Xn ∈ Xn (input marked by the vertical red line). The key step is computing the target set Xn using the sampled function fn, which generalizes posterior sampling for standard BO.
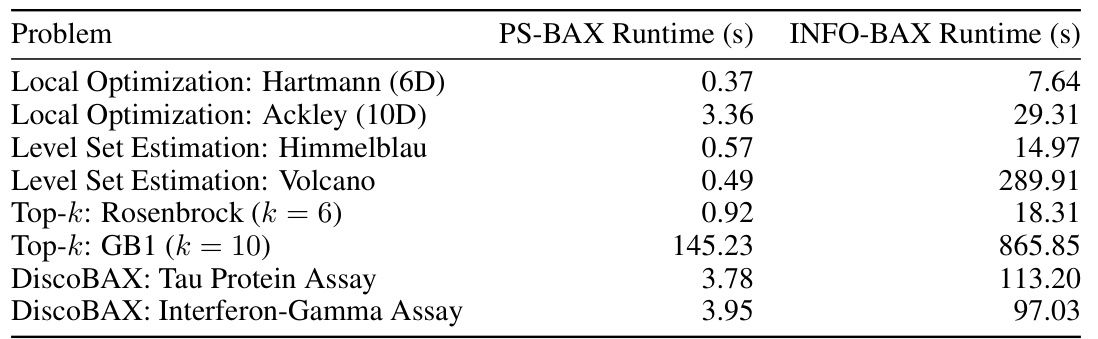
🔼 This table compares the average runtimes per iteration for PS-BAX and INFO-BAX algorithms across eight different problems, categorized into four problem classes. The results highlight the significantly faster performance of PS-BAX (one to three orders of magnitude) compared to INFO-BAX across all problems tested. The runtime difference is particularly noticeable in the Top-10 GB1 problem, attributed to the use of a deep kernel GP model.
read the caption
Table 1: Average runtimes per iteration of PS-BAX and INFO-BAX across our test problems. In all of them, PS-BAX is between one and three orders of magnitude faster than INFO-BAX. We also note that the runtimes for both algorithms are significantly longer on the Top-10 GB1 problem due to the use of a deep kernel GP model.
In-depth insights#
PS-BAX: A New BAX#
The proposed PS-BAX algorithm offers a novel approach to Bayesian algorithm execution (BAX) by leveraging posterior sampling. This contrasts with existing BAX methods that rely on computationally expensive expected information gain (EIG) calculations. PS-BAX’s simplicity and scalability are highlighted as key advantages, enabling efficient exploration of a wide range of problems including optimization and level set estimation. The algorithm’s core innovation lies in its ability to directly sample from the posterior distribution of the base algorithm’s output (target set), thereby avoiding the need for complex EIG optimization. Empirical results demonstrate competitive performance with existing methods, coupled with significant speed improvements. Crucially, the paper provides theoretical guarantees of asymptotic convergence under mild conditions, offering a deeper understanding of posterior sampling’s efficacy within the BAX framework. The combination of practical efficiency and theoretical soundness positions PS-BAX as a promising contribution to the field, potentially establishing a new baseline for future research.
Posterior Sampling#
Posterior sampling, a cornerstone of Bayesian methods, offers a powerful approach to algorithm execution (BAX). Instead of relying on computationally expensive expected information gain (EIG) calculations, posterior sampling directly leverages the posterior distribution of the function. This involves sampling a function from the posterior distribution, running the base algorithm on this sample, and selecting points based on the resulting output. This approach makes BAX significantly more efficient, especially in high-dimensional problems or when the property of interest is complex. The simplicity of implementation and ease of parallelization are significant advantages. Theoretical convergence guarantees offer additional confidence, solidifying posterior sampling as a robust and scalable method for BAX. While the applicability may be narrower than EIG-based approaches, its efficiency and theoretical underpinnings position it as a strong contender and a valuable benchmark for future research in BAX.
PS-BAX Efficiency#
The PS-BAX algorithm demonstrates significant computational efficiency advantages over existing Bayesian Algorithm Execution (BAX) methods. Its core innovation lies in replacing the computationally expensive expected information gain (EIG) criterion with posterior sampling. This simplification drastically reduces the runtime, particularly beneficial in high-dimensional problems or when the property of interest is complex. PS-BAX only requires a single base algorithm execution per iteration, unlike EIG-based methods that demand multiple executions and optimizations, resulting in substantial speed-ups. This efficiency is further enhanced by the algorithm’s inherent parallelizability, allowing for further computational gains. The reduced computational complexity of PS-BAX makes it a strong candidate for real-world applications where computational resources are constrained.
Convergence Proofs#
Convergence proofs in the context of Bayesian optimization algorithms are crucial for establishing the reliability and efficiency of these methods. They provide mathematical guarantees that the algorithm will, under certain assumptions, ultimately converge to the true optimum or a satisfactory solution. Asymptotic convergence is a common focus, proving convergence as the number of iterations or data points tends towards infinity. These proofs often rely on assumptions regarding the properties of the objective function (e.g., continuity, smoothness) and the probabilistic model used (e.g., Gaussian process priors). Demonstrating convergence can involve showing that the uncertainty in the estimated solution decreases over time, or that the sequence of points sampled by the algorithm converges to an optimal set. The key challenge lies in balancing the theoretical rigor of the proofs with the practical applicability of the assumptions. Real-world problems rarely meet all ideal conditions, so a careful consideration of the limitations and assumptions is important when interpreting convergence results.
Future Directions#
Future research could explore extensions of PS-BAX to handle noisy or incomplete data, a common challenge in real-world applications. Investigating alternative probabilistic models beyond Gaussian processes could broaden PS-BAX’s applicability and improve its performance on diverse problem types. Another avenue is developing more sophisticated acquisition functions to select evaluation points more effectively, potentially combining the strengths of posterior sampling with other acquisition strategies. Furthermore, research on theoretical guarantees for PS-BAX under more relaxed assumptions would strengthen its foundation and guide future algorithm design. Finally, applying PS-BAX to more complex real-world problems across various domains (beyond the examples presented) would demonstrate its broader utility and robustness.
More visual insights#
More on figures
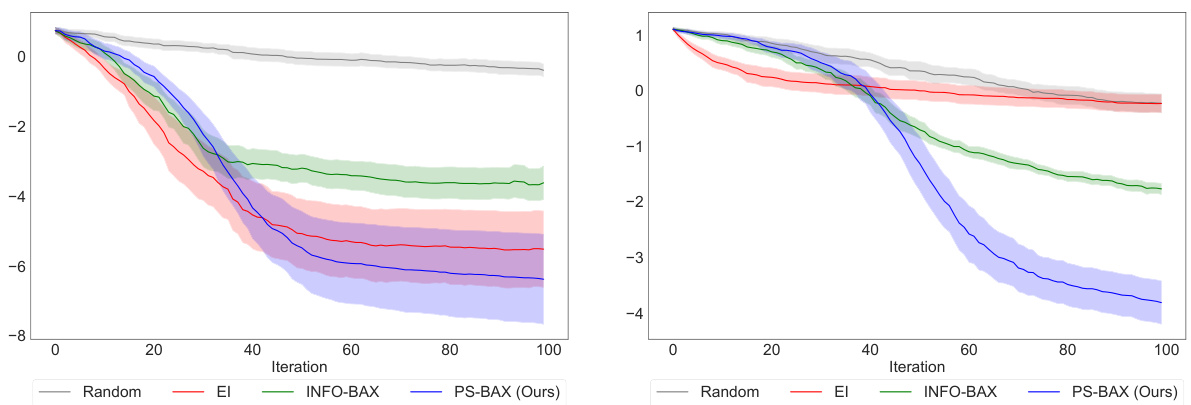
🔼 This figure compares the performance of PS-BAX against INFO-BAX and other algorithms on two local optimization problems: Hartmann-6D and Ackley-10D. The y-axis shows the log10 inference regret (lower is better), indicating how close the algorithm’s estimate is to the true optimum. The x-axis represents the iteration number. The shaded regions show the standard error across multiple runs. The results demonstrate that PS-BAX performs comparably to EI on Hartmann-6D but significantly outperforms all other methods on Ackley-10D.
read the caption
Figure 2: Results for Local Optimization, showing the log10 inference regret achieved by the compared algorithms (lower values indicate better performance). The left and right panels present results for the Hartmann-6D and Ackley-10D functions, respectively. On Hartmann-6D, PS-BAX and EI perform comparably, both outperforming INFO-BAX. On Ackley-10D, PS-BAX achieves significantly better results than the rest of the algorithms.
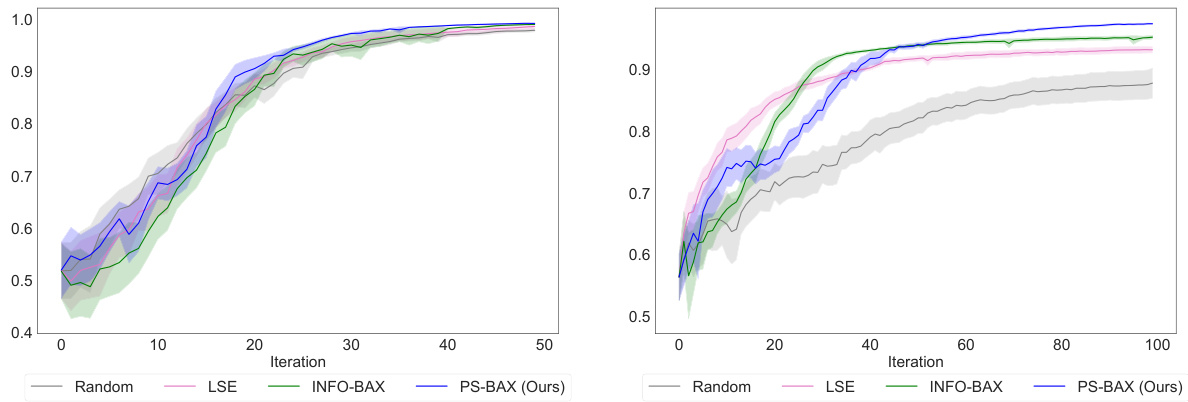
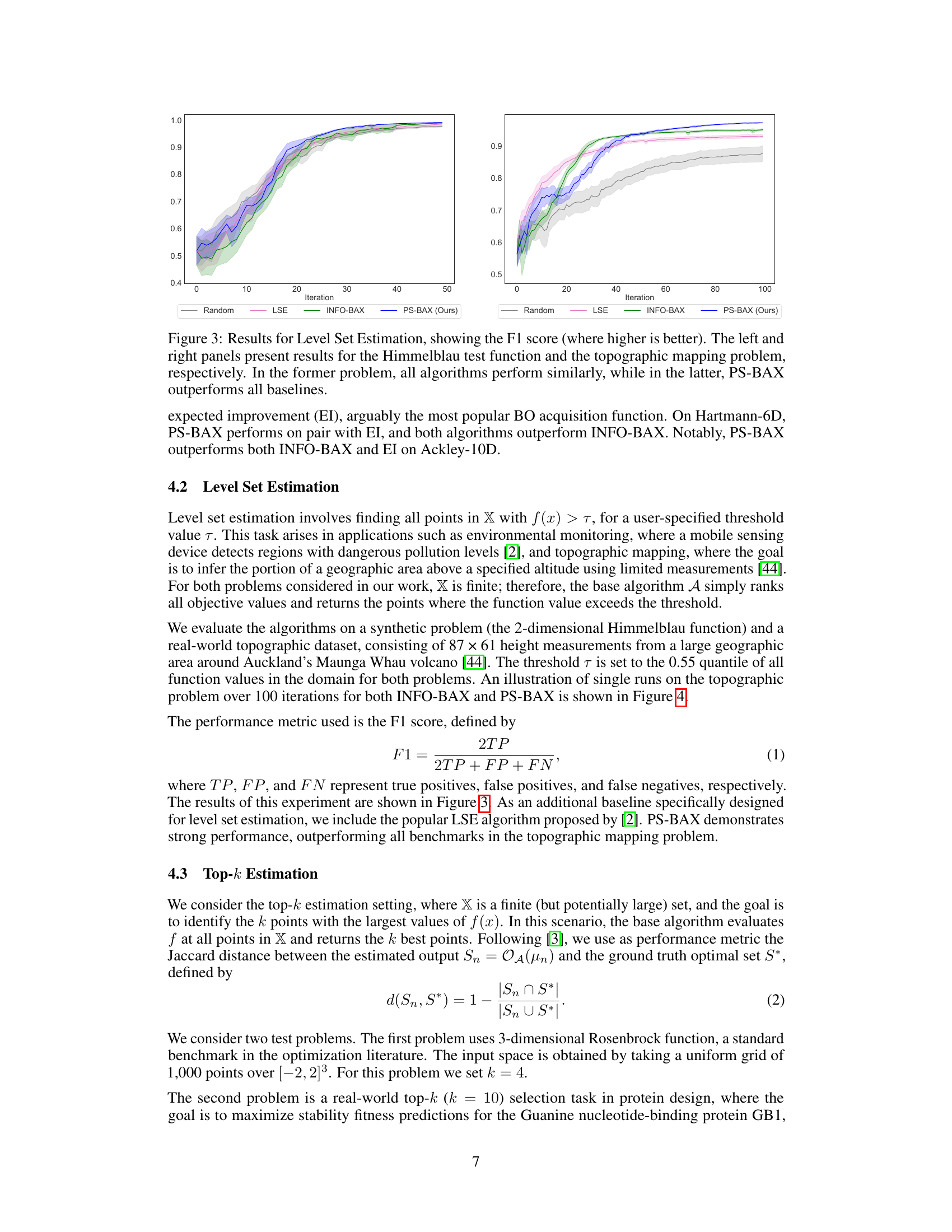
🔼 This figure displays the F1 scores for level set estimation across different algorithms. The left panel shows results for the Himmelblau function, where all algorithms perform similarly. In contrast, the right panel (topographic mapping problem) clearly shows PS-BAX substantially outperforming other methods like INFO-BAX, LSE, and random sampling.
read the caption
Figure 3: Results for Level Set Estimation, showing the F1 score (where higher is better). The left and right panels present results for the Himmelblau test function and the topographic mapping problem, respectively. In the former problem, all algorithms perform similarly, while in the latter, PS-BAX outperforms all baselines.

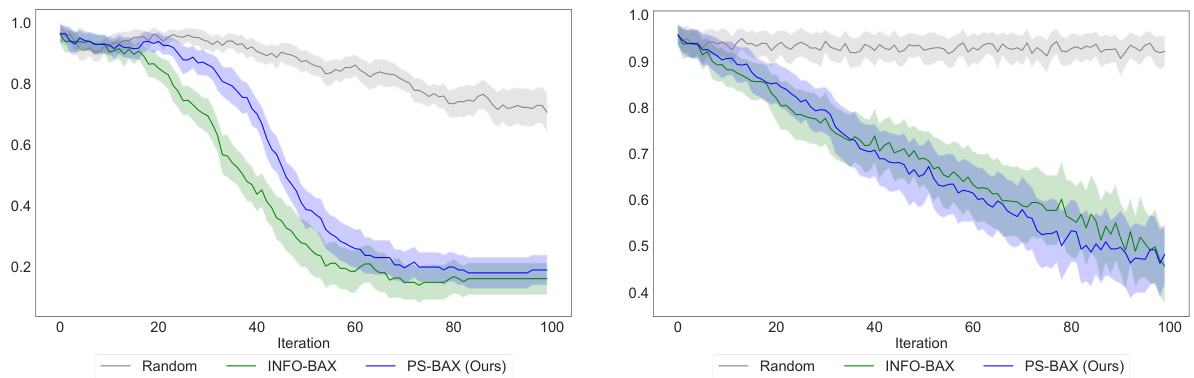
🔼 This figure compares the performance of INFO-BAX and PS-BAX on a topographic level set estimation problem. The left panel shows INFO-BAX’s results, demonstrating that it fails to accurately identify a significant portion of the target set (the area above a given threshold). In contrast, the right panel presents PS-BAX’s results, illustrating its success in accurately estimating the level set. Both algorithms are shown after 100 iterations; the ground truth super-level set and the points evaluated are also shown for context.
read the caption
Figure 4: Depiction of the INFO-BAX (left) and PS-BAX (right) algorithms on the topographic level set estimation problem described in Section 4.2. Each figure shows the ground truth super-level set (small black dots), the points evaluated after 100 iterations (green and blue dots for INFO-BAX and PS-BAX, respectively), and the estimated level set from the final posterior mean (red dots). PS-BAX provides an accurate estimate of the level set, whereas INFO-BAX misses a significant portion.
🔼 This figure compares the performance of PS-BAX, INFO-BAX, LSE, and random sampling methods on two level set estimation problems. The F1 score is used as the performance metric. The results show that PS-BAX outperforms the other methods on the topographic mapping problem, while all methods perform similarly on the Himmelblau problem.
read the caption
Figure 3: Results for Level Set Estimation, showing the F1 score (where higher is better). The left and right panels present results for the Himmelblau test function and the topographic mapping problem, respectively. In the former problem, all algorithms perform similarly, while in the latter, PS-BAX outperforms all baselines.
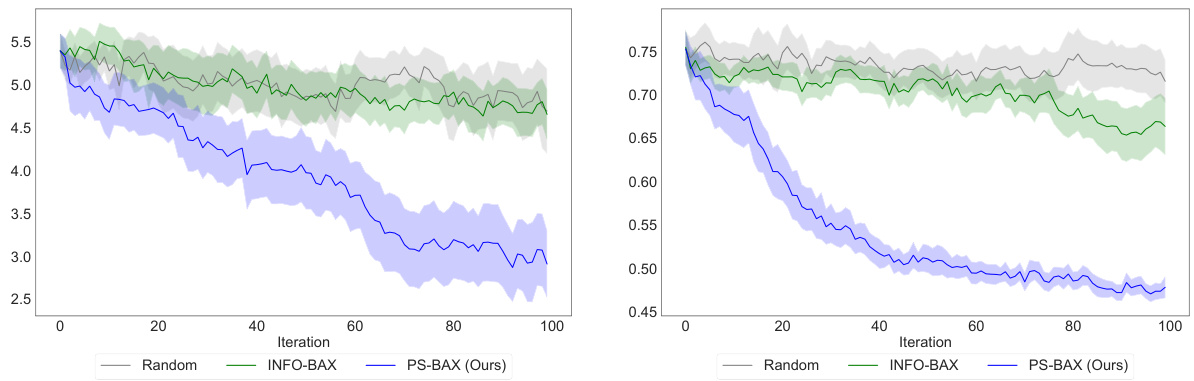
🔼 This figure displays the results of applying PS-BAX and INFO-BAX to two drug discovery problems from the DiscoBAX framework. The performance metric is regret, which measures the difference between the optimal solution found using the true function and the solution obtained using the posterior mean. Both problems use the Achilles dataset, and the results show that PS-BAX outperforms INFO-BAX significantly, and INFO-BAX only marginally outperforms random sampling in both cases.
read the caption
Figure 6: Results for DiscoBAX [29], showing the regret between the solution found by applying a greedy submodular optimization algorithm to the objective in Equation 3 and the solution obtained from applying the same algorithm over the posterior mean instead of the true function. Both problems are based on the Achilles dataset [50], with the left panel presenting results for the tau protein assay [48] and the right panel showing results for the interferon-gamma assay. In both cases, PS-BAX significantly outperforms INFO-BAX, which performs only marginally better than Random.
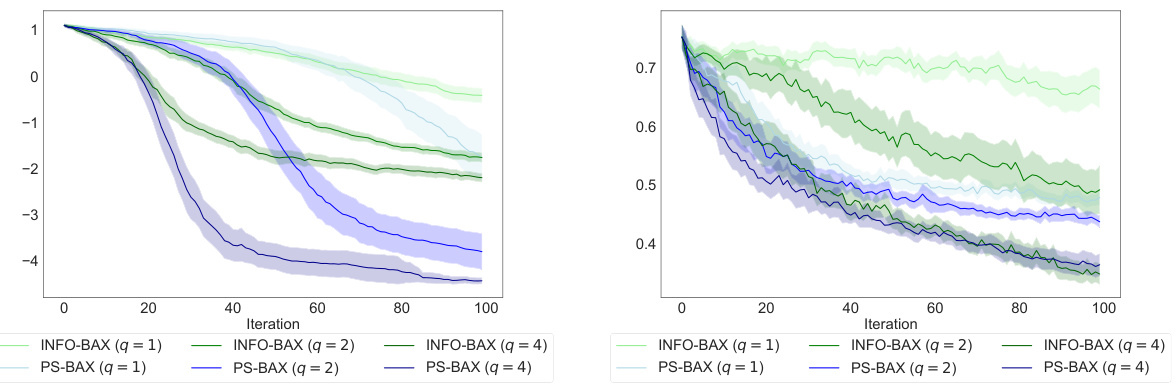
🔼 This figure compares the performance of PS-BAX and INFO-BAX algorithms with different batch sizes (q=1, 2, 4) on two distinct problems: the Ackley-10D local optimization problem and the DiscoBAX interferon-gamma assay problem. The x-axis represents the number of iterations, and the y-axis likely shows a performance metric (the specific metric isn’t explicitly mentioned in the provided caption, but it is likely a measure of error or regret). The plot shows that PS-BAX generally performs similarly to or better than INFO-BAX, and that increasing the batch size can improve performance for both algorithms. The shaded areas around the lines likely represent confidence intervals.
read the caption
Figure 7: Performance of PS-BAX and INFO-BAX under batch sizes q = 1,2,4 on the local optimization Ackley-10D problem (left) and the DiscoBAX interferon-gamma essay problem (right).
Full paper#