Are More LLM Calls All You Need? Towards the Scaling Properties of Compound AI Systems

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it challenges the common assumption that more language model (LM) calls always improve compound AI system performance. This finding necessitates a re-evaluation of resource allocation in compound AI development and opens exciting avenues for optimizing these systems. The analytical model provided is also a significant contribution, enabling researchers to predict optimal LM call numbers and saving computational resources.

Visual Insights

#

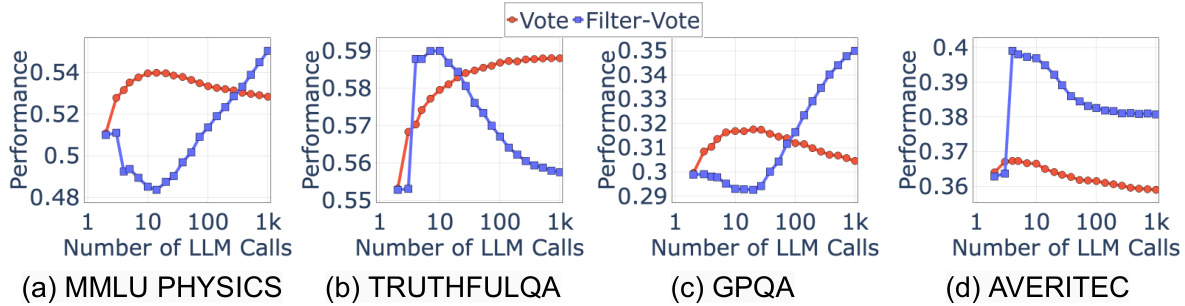
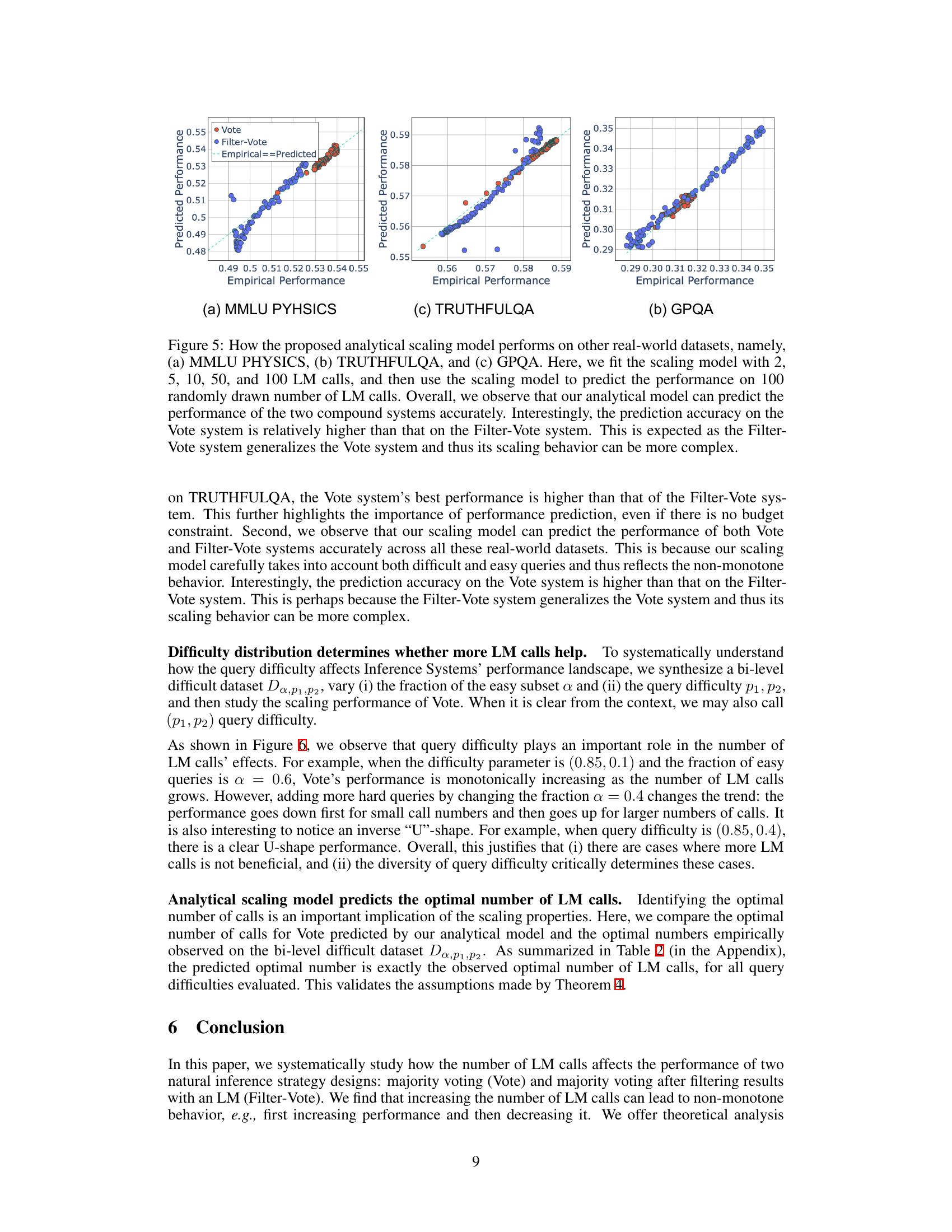
This figure displays the scaling behavior of two compound AI systems, Vote and Filter-Vote, across four different language tasks (MMLU Physics, TruthfulQA, GPQA, and Averitec). The x-axis represents the number of language model (LM) calls made by the system, and the y-axis represents the system’s performance. The surprising finding is that performance is not always monotonically increasing with the number of LM calls. In some cases, performance improves initially, then decreases; in others, it decreases and then increases. This non-monotonic relationship highlights the complexity of compound AI systems and the need for a deeper understanding of how to optimize their design.

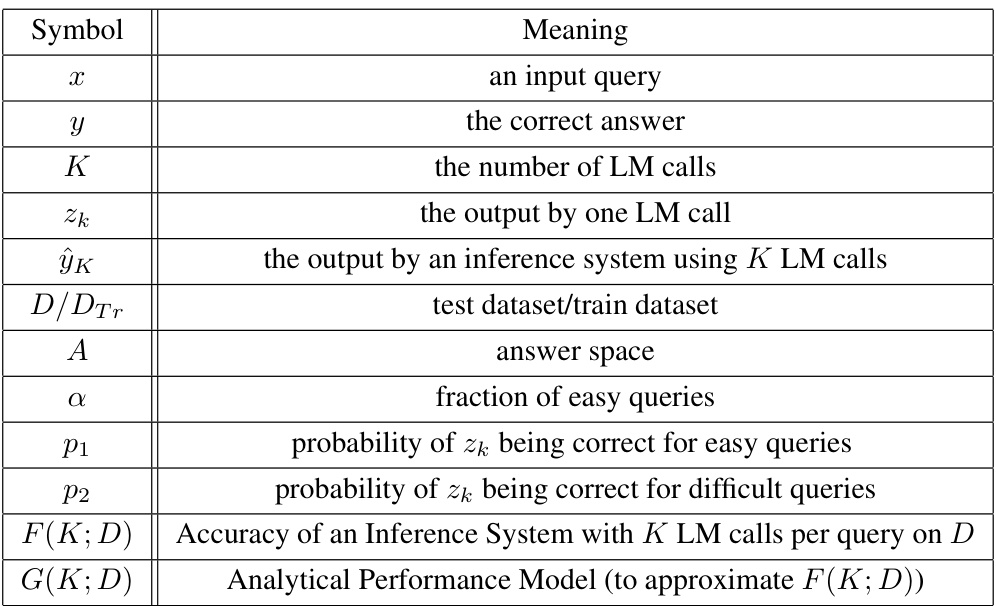
This table lists notations used in the paper. It defines symbols used for key concepts such as input query, correct answer, number of LM calls, output from one LM call, output from an inference system, datasets used (test and training), answer space, and the proportion of ’easy’ queries. It also defines symbols representing probabilities of correctness for easy and difficult queries. Finally, it shows symbols for the accuracy of the inference system and its analytical performance model.

In-depth insights

#

LM Call Scaling

#

The study of ‘LM Call Scaling’ reveals a surprising non-monotonic relationship between the number of language model (LM) calls and a compound AI system’s performance. Initially, increasing LM calls improves accuracy, but beyond a certain point, performance degrades. This counter-intuitive finding is attributed to the diversity of query difficulty within a given task. More LM calls benefit easier queries, but hurt harder ones. The optimal number of calls is dependent on the specific task’s difficulty distribution. A key contribution is a theoretical framework that models this non-monotonic behavior. This enables the prediction of optimal LM calls, maximizing accuracy without unnecessary computation, offering a crucial advance in optimizing resource allocation for compound AI systems.

Vote/Filter-Vote

#

The core of the proposed approach lies in analyzing the scaling properties of compound AI systems. The paper focuses on two fundamental system designs: Vote and Filter-Vote. Vote aggregates multiple predictions via majority voting, mirroring strategies like Gemini’s CoT@32. Filter-Vote refines this by incorporating an LM filter to remove potentially incorrect predictions before voting. The key finding is the surprising non-monotonicity of performance with respect to the number of LM calls. Both systems exhibit performance that initially improves but may then degrade as more LM calls are added. This unexpected behaviour stems from query difficulty diversity within a dataset. More calls boost accuracy on easy queries but hurt performance on hard ones, leading to a non-monotonic aggregate effect. This is further supported by theoretical models which accurately predict these non-monotonic trends, suggesting that the optimal number of calls is not simply more, but the number which best balances this trade-off between easy and hard queries. Thus, the paper proposes a valuable method for optimizing compound systems through careful consideration of query difficulty and its effect on scaling.

Query Difficulty

#

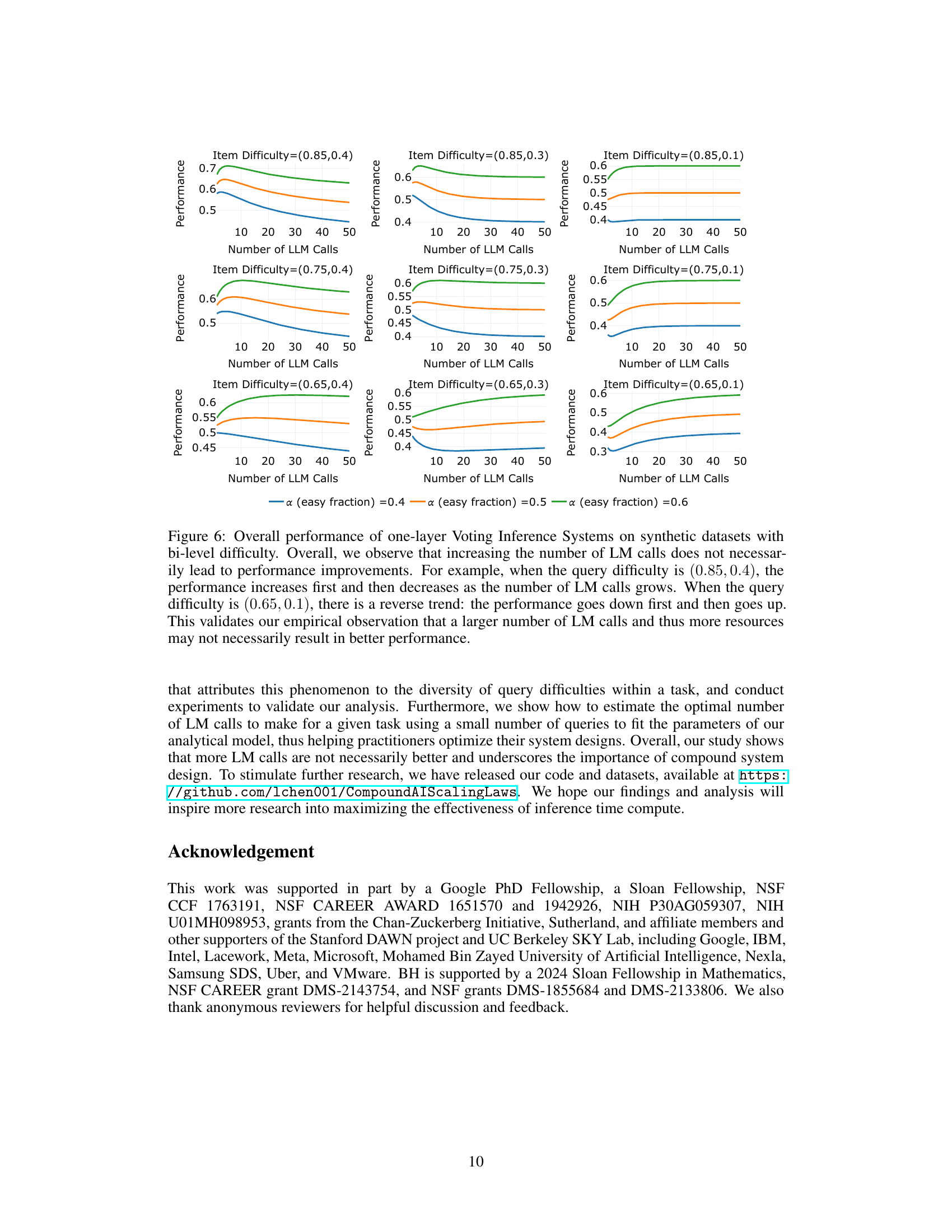
The concept of ‘Query Difficulty’ is central to the paper’s analysis of compound AI systems. The authors posit that a query’s inherent difficulty significantly impacts the system’s performance, particularly when multiple language model (LM) calls are aggregated. This difficulty isn’t simply a binary classification (easy/hard) but rather a spectrum. Easier queries show monotonic performance improvements with more LM calls, converging towards near-perfect accuracy. Conversely, harder queries exhibit a non-monotonic response, initially degrading in accuracy before potentially improving slightly with substantially increased calls. This non-monotonicity arises from the diverse difficulty levels within a given task. The framework introduced helps to precisely define query difficulty and provides an analytical model to understand and even predict this behaviour, thus allowing to optimize the number of LM calls for maximum overall accuracy.

Scaling Model

#

The research paper explores the scaling properties of compound AI systems, focusing on how the number of language model (LM) calls affects their performance. A core contribution is the development of a novel scaling model that predicts system performance as a function of the number of LM calls. This model is particularly insightful because it reveals a non-monotonic relationship: increasing LM calls doesn’t always improve performance; instead, an optimal number of calls exists, beyond which performance can degrade. The model’s strength lies in its ability to capture the interplay between easy and hard queries. It suggests that additional LM calls boost performance on easy queries but harm it on hard queries, and the optimal number of calls depends on the distribution of query difficulty within a task. This nuanced understanding allows for more efficient resource allocation and offers a potential method for optimizing compound AI systems without extensive experimentation.

Future Work

#

The paper’s core contribution lies in analyzing the scaling properties of compound AI systems. Future work should naturally explore extending these analyses to a broader range of compound AI system architectures beyond the simple Vote and Filter-Vote models considered. This includes investigating systems that utilize more sophisticated aggregation techniques, more complex filtering mechanisms, or incorporate diverse LM models. A key area is developing more robust theoretical models that can accurately predict system performance across various tasks and query difficulty distributions, going beyond the binary ’easy/hard’ classification used in this paper. Another crucial direction is incorporating cost into the performance analysis. The current work focuses only on accuracy, while practical deployment requires considering the computational resources and monetary expense associated with increasing the number of LM calls. Furthermore, empirical studies on a wider range of tasks, including those with subjective evaluation, are necessary to fully validate the observed non-monotonic scaling behavior. Lastly, researchers could investigate how the optimal number of LM calls interacts with other model parameters, such as temperature or prompt engineering, to achieve a more holistic and comprehensive understanding of compound AI systems’ scaling laws.

More visual insights

#

More on figures

The figure shows the performance of Vote and Filter-Vote models on four different datasets (MMLU Physics, TruthfulQA, GPQA, and Averitec) as the number of language model (LM) calls increases. Surprisingly, the performance is not consistently increasing with more LM calls; instead, it often shows a non-monotonic trend, initially increasing, then decreasing or vice versa, depending on the dataset and the model.

This figure shows the performance of Vote and Filter-Vote models on four different datasets (MMLU Physics, TruthfulQA, GPQA, and AVERITEC) as the number of LM calls increases. It demonstrates a surprising non-monotonic relationship: performance does not always increase with the number of calls. Instead, the performance first increases and then decreases for Vote in some cases (and the opposite pattern for Filter-Vote). This behavior is attributed to the diversity of query difficulties within the dataset.

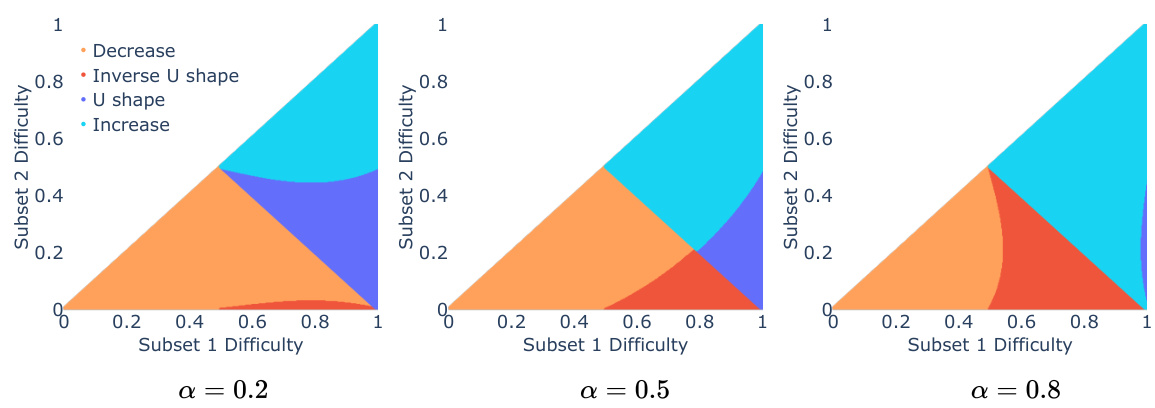
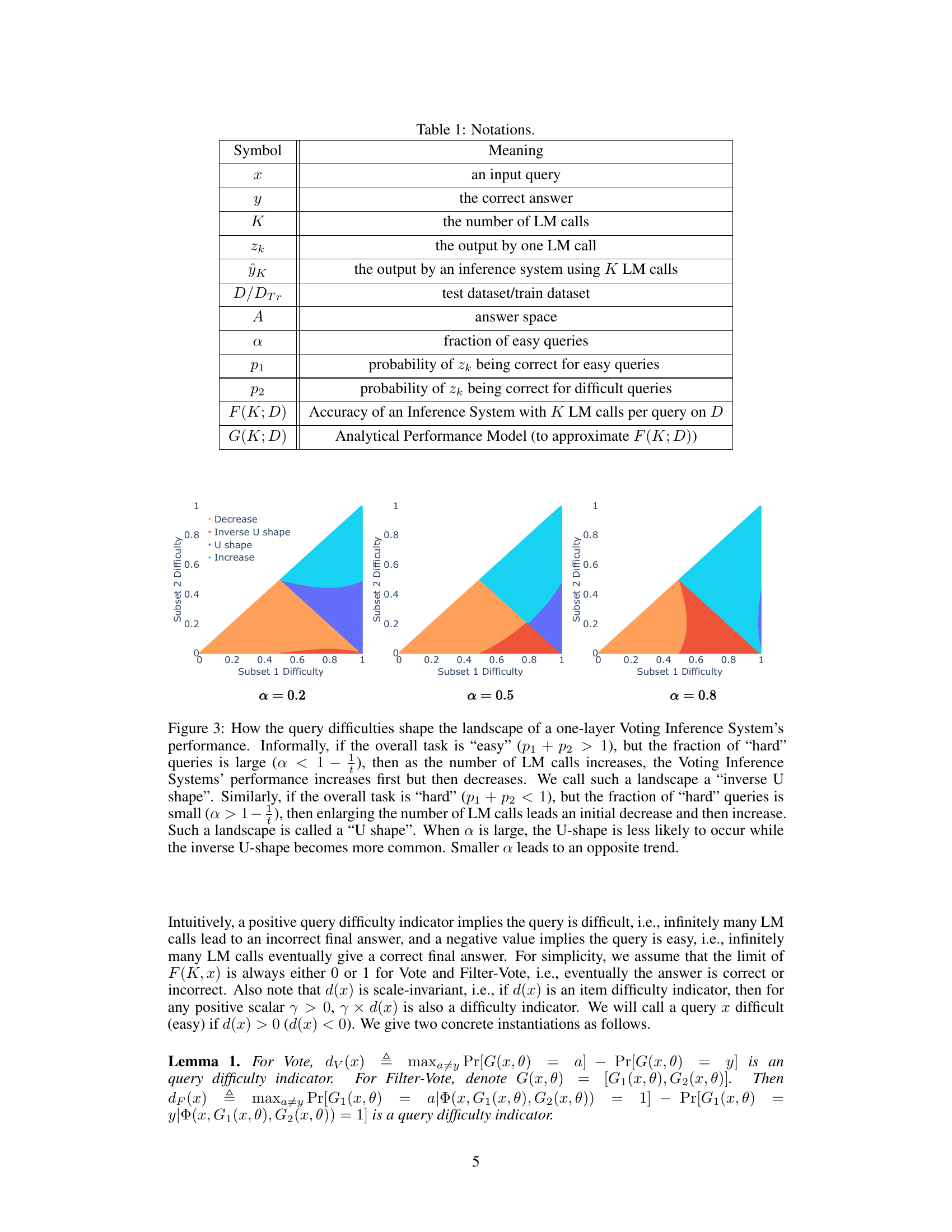
This figure shows how the difficulty of queries affects the performance of a Voting Inference System. The x-axis represents the difficulty of one subset of queries, and the y-axis represents the difficulty of another subset. The different colored regions represent different performance trends (increasing, decreasing, inverse U-shape, U-shape). The parameter ‘a’ controls the proportion of easy queries in the task, influencing which performance trend dominates.

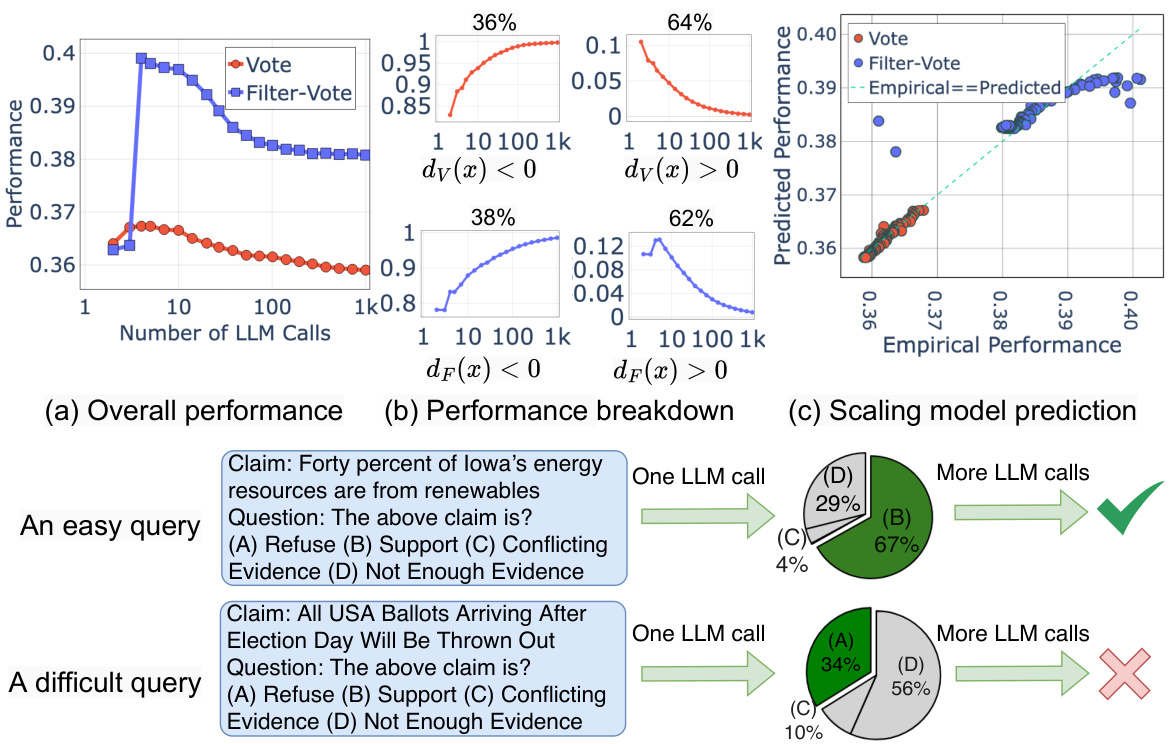
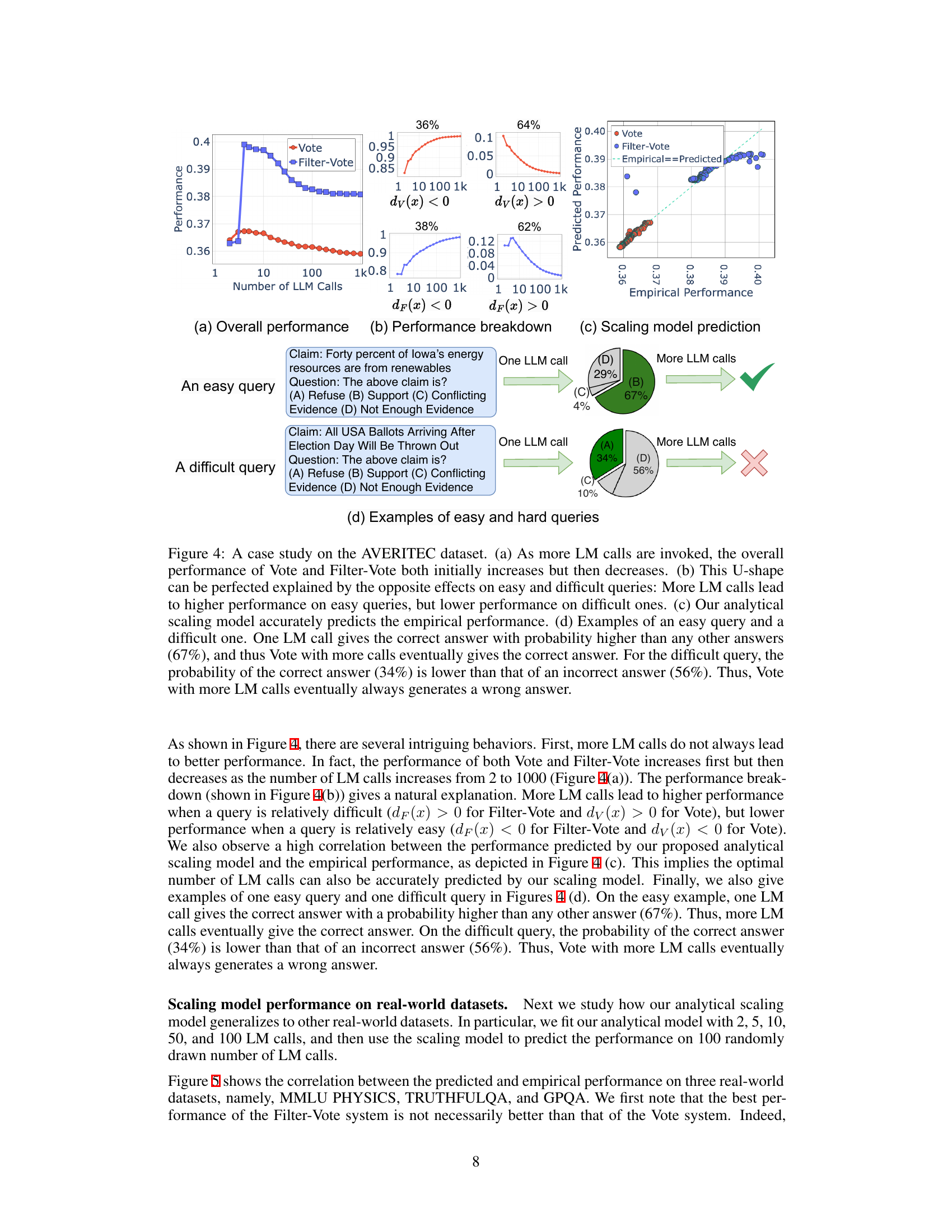
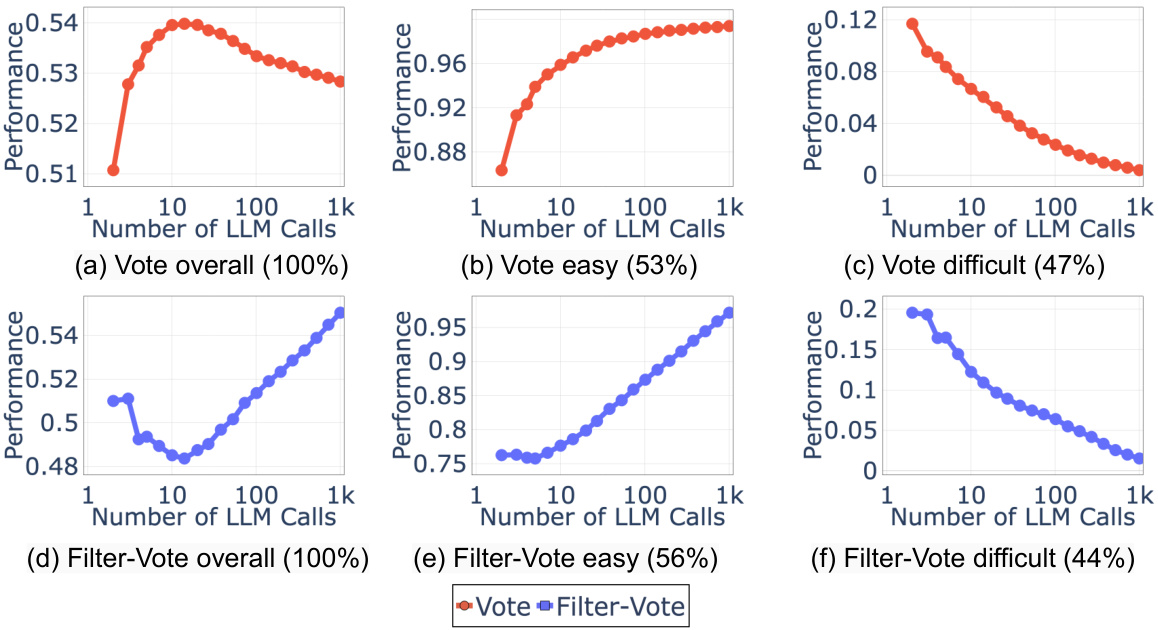
This figure shows a case study using the AVERITEC dataset to demonstrate the non-monotonic scaling behavior of Vote and Filter-Vote. The subfigures break down the overall performance (a) into performance on easy and difficult queries (b), showing that more LM calls improve easy queries but hurt hard queries. Subfigure (c) validates the accuracy of the analytical scaling model in predicting performance, and (d) provides example queries illustrating why this behavior occurs.

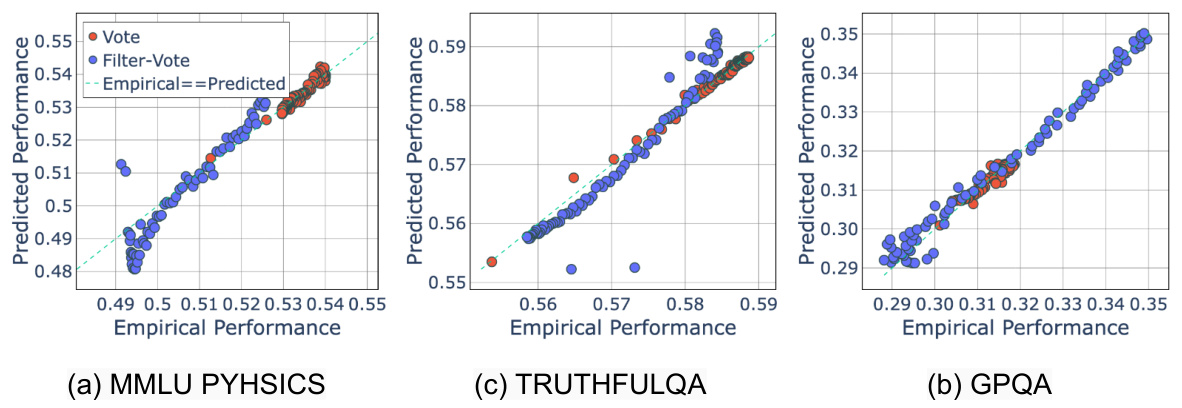
This figure displays the performance of Vote and Filter-Vote models across four different datasets (MMLU Physics, TruthfulQA, GPQA, and Averitec) as the number of Language Model (LM) calls increases. The key observation is the non-monotonic relationship between the number of LM calls and model performance. In some cases, performance improves initially with more LM calls, but then begins to decline; while in others, the opposite is true – performance dips initially before improving with more calls. This unexpected behavior highlights the complexities of scaling compound AI systems.

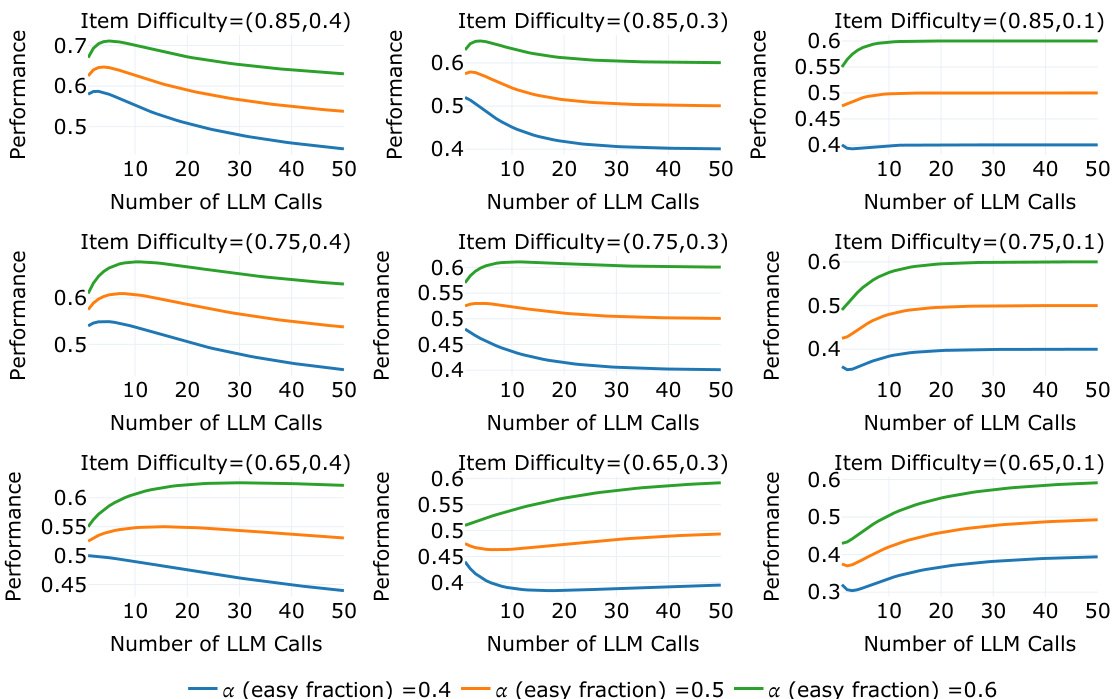
This figure shows the performance of Vote and Filter-Vote models on the MMLU Physics dataset, broken down by query difficulty. It demonstrates that increasing the number of LM calls improves performance on easier queries but reduces performance on more challenging ones. This non-monotonic behavior helps to explain the overall non-monotonic scaling properties observed in Figure 1.

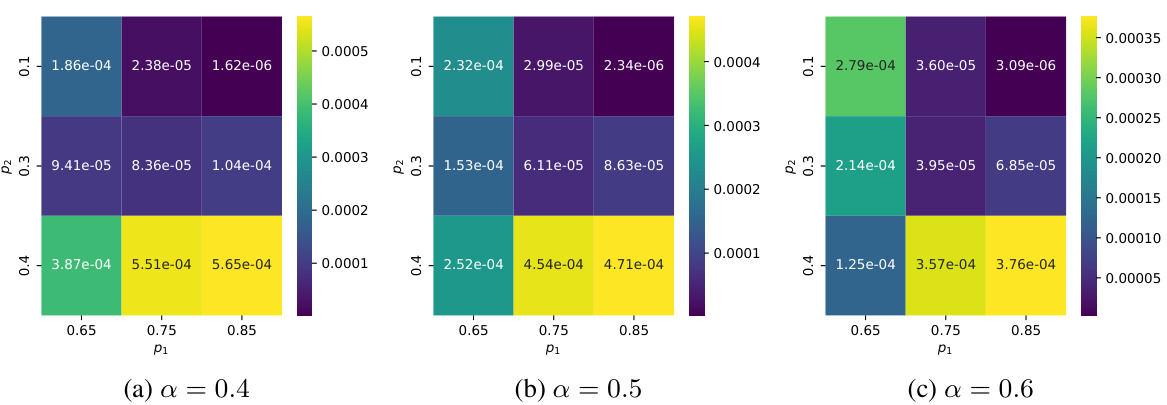
This figure shows the mean squared error between the predicted performance using the analytical scaling model and the actual performance of the Vote model on synthetic datasets with varying bi-level difficulties. The model is fit using performance data from 1 to 5 LM calls, and then its predictions are evaluated across a range of 1-100 calls. The results show that the model’s predictions closely match the actual performance, highlighting the accuracy of the scaling law in capturing the relationship between the number of LM calls and the performance.

Full paper

#