TL;DR#
Ensemble methods, combining predictions from multiple models, are increasingly popular for improving classification accuracy. However, building many models can be computationally costly and the performance gains often diminish. This research directly addresses these issues by focusing on the relationship between classifier disagreement and overall ensemble performance. It highlights the limitations of existing methods, which often fail to accurately predict the final ensemble accuracy.
The study proposes a novel metric, ‘polarization’, to quantify the spread of errors among classifiers. Using polarization, it develops new, tighter upper bounds for the error rate of a majority vote classifier. Importantly, the study establishes a theoretical framework for predicting the performance of a large ensemble using just a few classifiers. This is achieved by analyzing the asymptotic behavior of disagreement as the number of classifiers increases. The theoretical findings are supported by empirical results on image classification tasks, which demonstrate the effectiveness of the proposed approach.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel approach to optimize ensemble performance in classification tasks. By introducing the concept of polarization and providing tight error bounds, it provides researchers with practical tools to predict the performance of larger ensembles based on smaller ones. This is especially relevant in the current landscape of large neural networks where scaling models becomes increasingly expensive. The findings open up new avenues of research in ensemble methods, impacting model efficiency and improving accuracy in various applications.
Visual Insights#
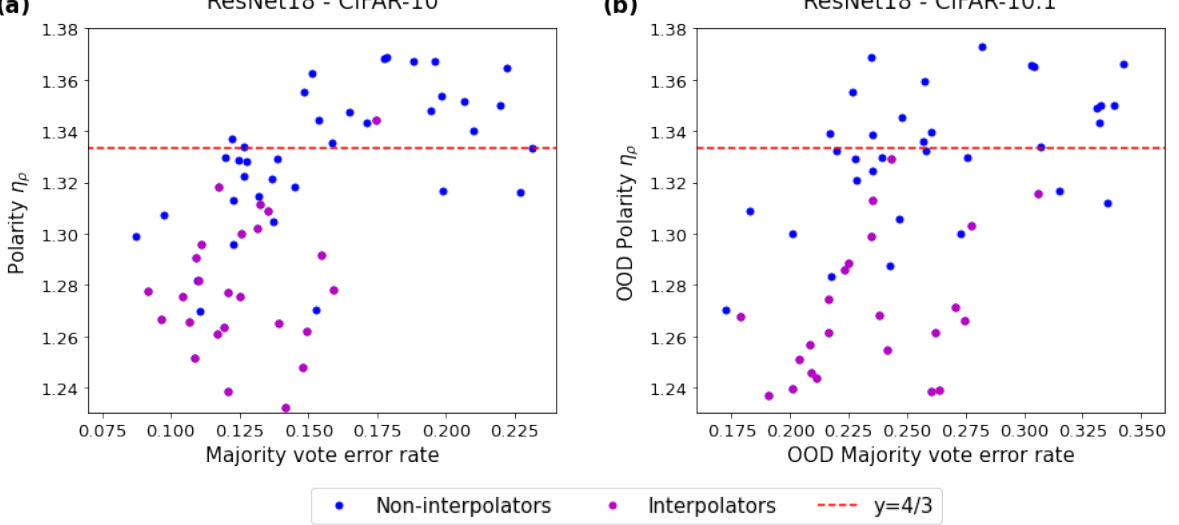
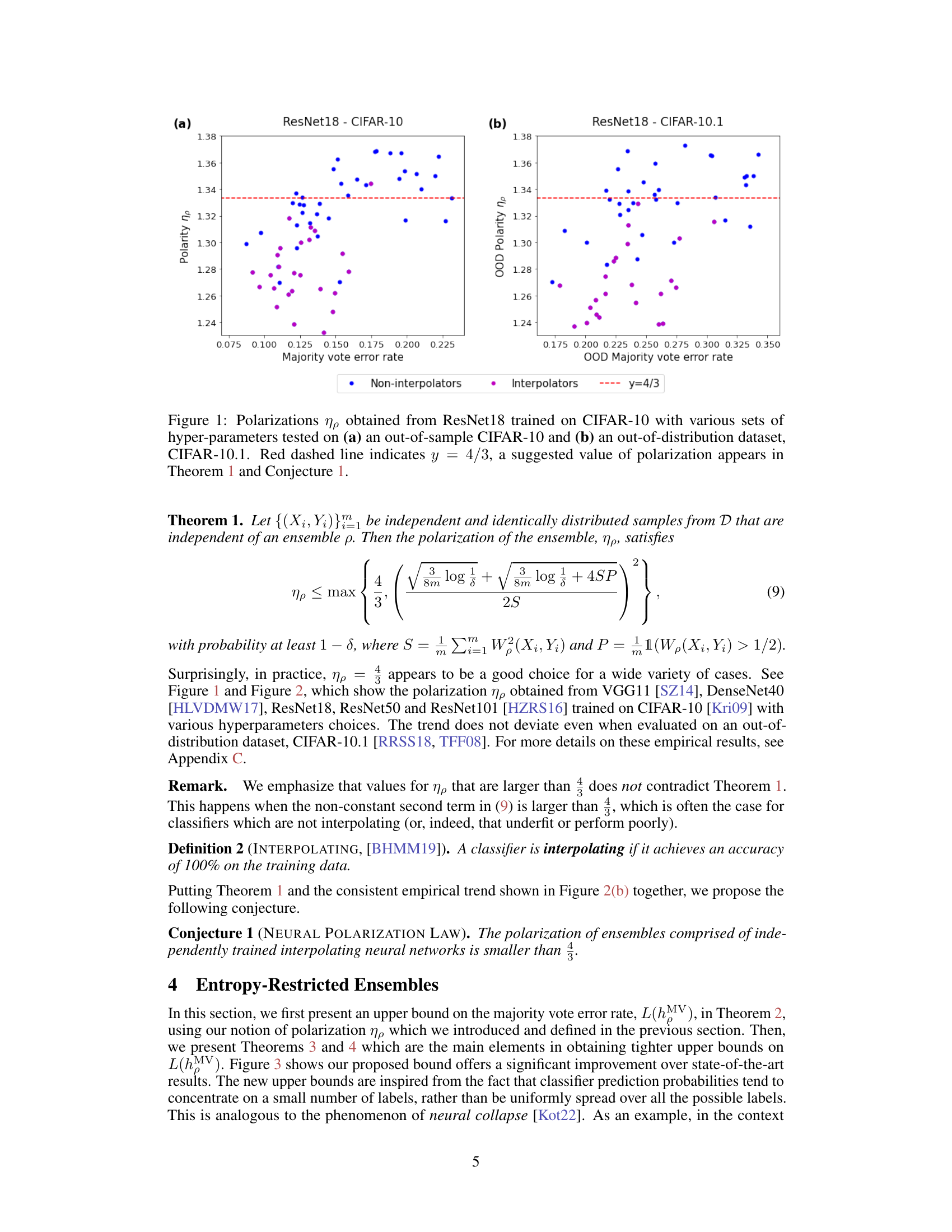
🔼 This figure shows the polarization (ηρ) values obtained from ResNet18 models trained on CIFAR-10, tested on both in-distribution (CIFAR-10) and out-of-distribution (CIFAR-10.1) datasets. Each point represents a different set of hyperparameters used during training. The red dashed line represents the theoretical value of 4/3, which is predicted by the neural polarization law proposed in the paper. The figure aims to support the conjecture that interpolating neural networks have a polarization close to 4/3, regardless of the dataset or hyperparameters.
read the caption
Figure 1: Polarizations ηρ obtained from ResNet18 trained on CIFAR-10 with various sets of hyper-parameters tested on (a) an out-of-sample CIFAR-10 and (b) an out-of-distribution dataset, CIFAR-10.1. Red dashed line indicates y = 4/3, a suggested value of polarization appears in Theorem 1 and Conjecture 1.
In-depth insights#
Ensemble Polarization#
Ensemble polarization, a novel concept in ensemble methods, explores the dispersion of classifier error rates around the true label. It provides a more nuanced understanding than simple disagreement, which only measures the difference between individual classifier outputs. High polarization signifies that classifiers tend to cluster around either correct or incorrect predictions, indicating a strong, although potentially flawed, consensus. Lower polarization suggests a more diverse range of predictions, making it harder to form a definitive consensus through aggregation. This insight allows for a more accurate prediction of ensemble performance and optimization of ensemble size. The concept links disagreement to error rate by introducing a polarizing factor, potentially leading to tighter error bounds and more accurate prediction of ensemble performance improvements with increased classifier numbers. Analyzing polarization helps to characterize the quality and informativeness of an ensemble, especially relevant in high-dimensional spaces where simple disagreement alone may be insufficient. The empirical validation of the proposed neural polarization law, demonstrating the near-constant polarization behavior across diverse network models and hyperparameters, is crucial for broader adoption of this insightful approach in machine learning.
Majority Vote Error#
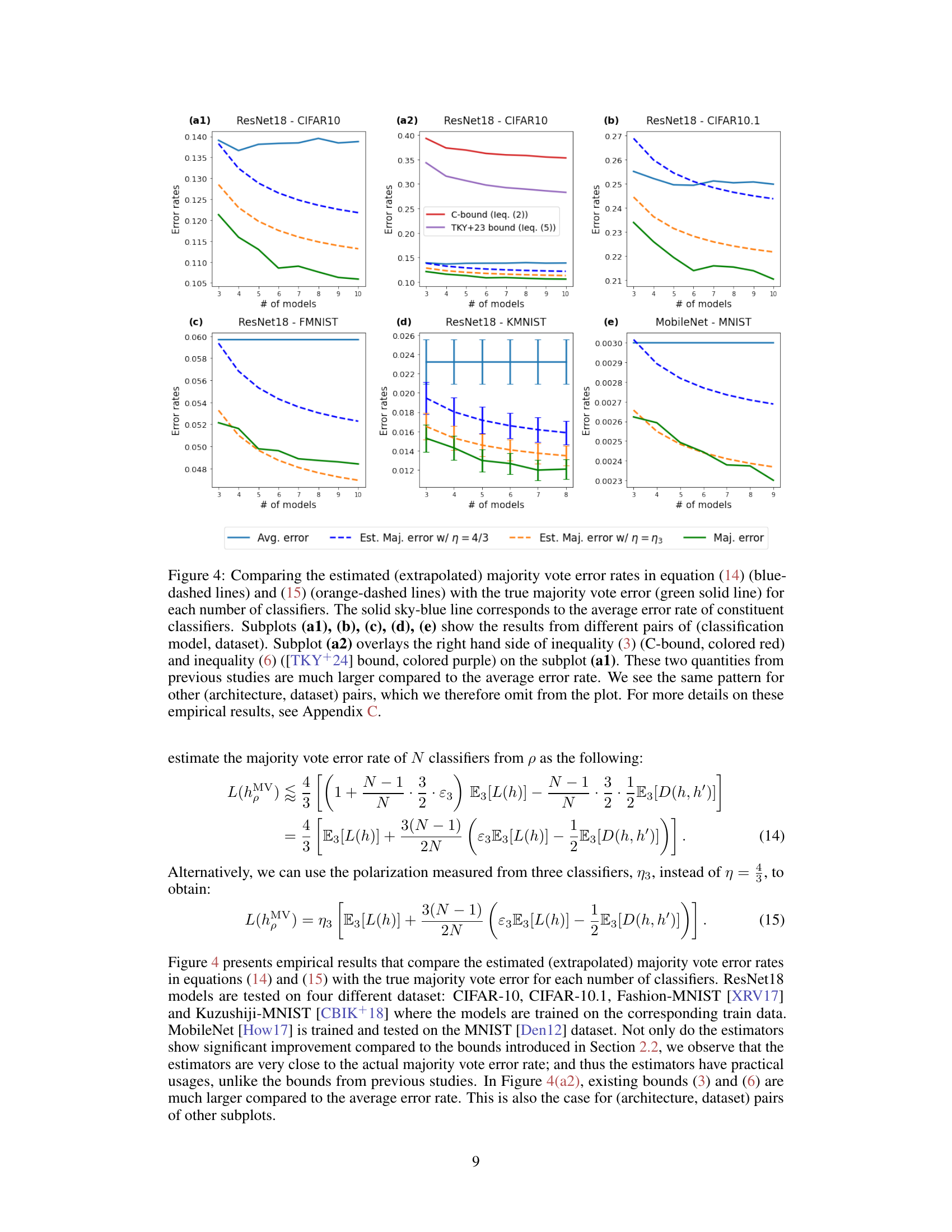
The concept of “Majority Vote Error” centers on the discrepancy between the prediction of an ensemble of classifiers and the true label. It’s a crucial metric for evaluating the performance of ensemble methods. A lower error indicates better collective decision-making. Understanding this error requires analyzing individual classifier performance and the interplay among them. Factors influencing this error include the diversity of classifiers, their individual accuracy, and the underlying data distribution. High diversity can reduce error, but it’s not sufficient on its own; accurate individual classifiers are also crucial. The paper delves into techniques to estimate this error, exploring theoretical bounds and highlighting the influence of polarization and disagreement among classifiers. The research emphasizes how polarization, a measure of higher-order dispersity of error rates, impacts the error rate. By restricting entropy or applying specific conditions on the ensemble, improved, tighter bounds on the error are achievable. This offers valuable insights into ensemble performance prediction.
Asymptotic Disagreement#
The concept of ‘Asymptotic Disagreement’ in the context of ensemble classifiers examines how the degree of disagreement among classifiers changes as the number of classifiers grows. A key insight is that disagreement doesn’t necessarily increase indefinitely. Instead, under certain conditions (like those explored in the paper, such as restricted entropy), it may stabilize or even decrease. This stabilization point has significant implications for predicting the performance of larger ensembles. Understanding the asymptotic behavior of disagreement is crucial for determining when adding more classifiers yields diminishing returns; this allows researchers to optimize the size of an ensemble and avoid unnecessary computational costs. The paper likely provides mathematical analysis (e.g., bounds, convergence theorems) to support this claim, showing how this asymptotic behavior relates to the ensemble’s final error rate and overall accuracy. Analyzing asymptotic disagreement helps bridge the gap between theoretical understanding and practical application of ensemble methods. It allows for more efficient and cost-effective ensemble design, a major concern in modern machine learning applications where scaling can be computationally expensive.
Competence Limits#
The concept of ‘Competence Limits’ in ensemble methods centers on the conditions under which combining multiple classifiers consistently improves predictive accuracy. A crucial limitation is the assumption of classifier competence, meaning that, on average, a majority of classifiers are correct. When this assumption breaks down, due to factors like highly correlated errors or classifiers performing poorly, the benefits of ensembling diminish significantly. Understanding these limitations requires investigation into the distribution of errors and disagreement among classifiers. The paper might explore the boundaries of competence, defining specific metrics or conditions to predict when ensemble methods are most effective. A significant focus would likely be on the relationship between error correlation, polarization of classifiers, and the overall performance of the ensemble. Failing to account for competence limits may lead to erroneous predictions of ensemble performance, as the benefits of aggregation are contingent on the underlying competence of individual classifiers. Ultimately, research in competence limits strives to provide clear guidelines for choosing and utilizing ensemble techniques, clarifying when ensembling is beneficial and when it is not. The paper’s analysis of polarization and restricted entropy conditions are potentially crucial in defining these boundaries.
Future Research#
The paper’s core contribution is a novel theoretical framework for understanding ensemble performance, particularly in the context of neural networks. Future research could focus on extending this framework to address settings beyond majority voting, such as weighted averaging or other ensemble methods. Investigating the impact of different types of neural network architectures and training procedures on polarization and disagreement would be valuable. Empirically validating the neural polarization law across a wider variety of datasets and model architectures is crucial. Furthermore, developing more practical and accurate methods for estimating the key quantities (polarization and disagreement) from a small number of classifiers, thereby improving the accuracy of the performance prediction, would be a significant advancement. Exploring the relationship between the asymptotic behavior of the disagreement and the generalization performance is essential for advancing this research. Finally, investigating the applicability of this framework to other machine learning tasks and domains beyond image classification would broaden its impact.
More visual insights#
More on figures
🔼 This figure shows the polarization (ηρ) values obtained from various experiments using ResNet18 trained on CIFAR-10. The experiments vary hyperparameters and test on both in-distribution (CIFAR-10) and out-of-distribution (CIFAR-10.1) datasets. The plots illustrate that the polarization is relatively constant across different hyperparameter settings and datasets, and is approximately 4/3. This supports the paper’s Conjecture 1, the Neural Polarization Law, suggesting that most interpolating neural network models have a polarization of 4/3.
read the caption
Figure 1: Polarizations ηρ obtained from ResNet18 trained on CIFAR-10 with various sets of hyper-parameters tested on (a) an out-of-sample CIFAR-10 and (b) an out-of-distribution dataset, CIFAR-10.1. Red dashed line indicates y = 4/3, a suggested value of polarization appears in Theorem 1 and Conjecture 1.
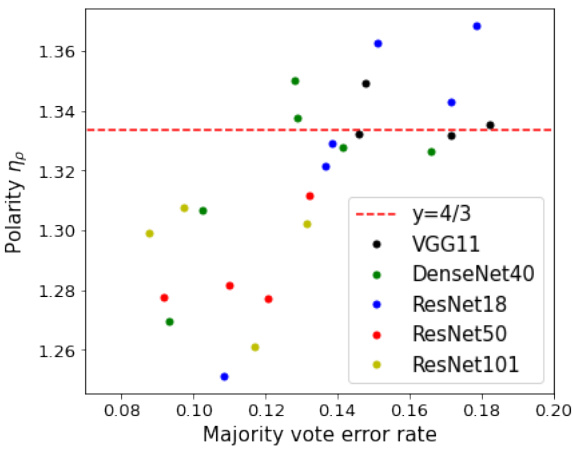
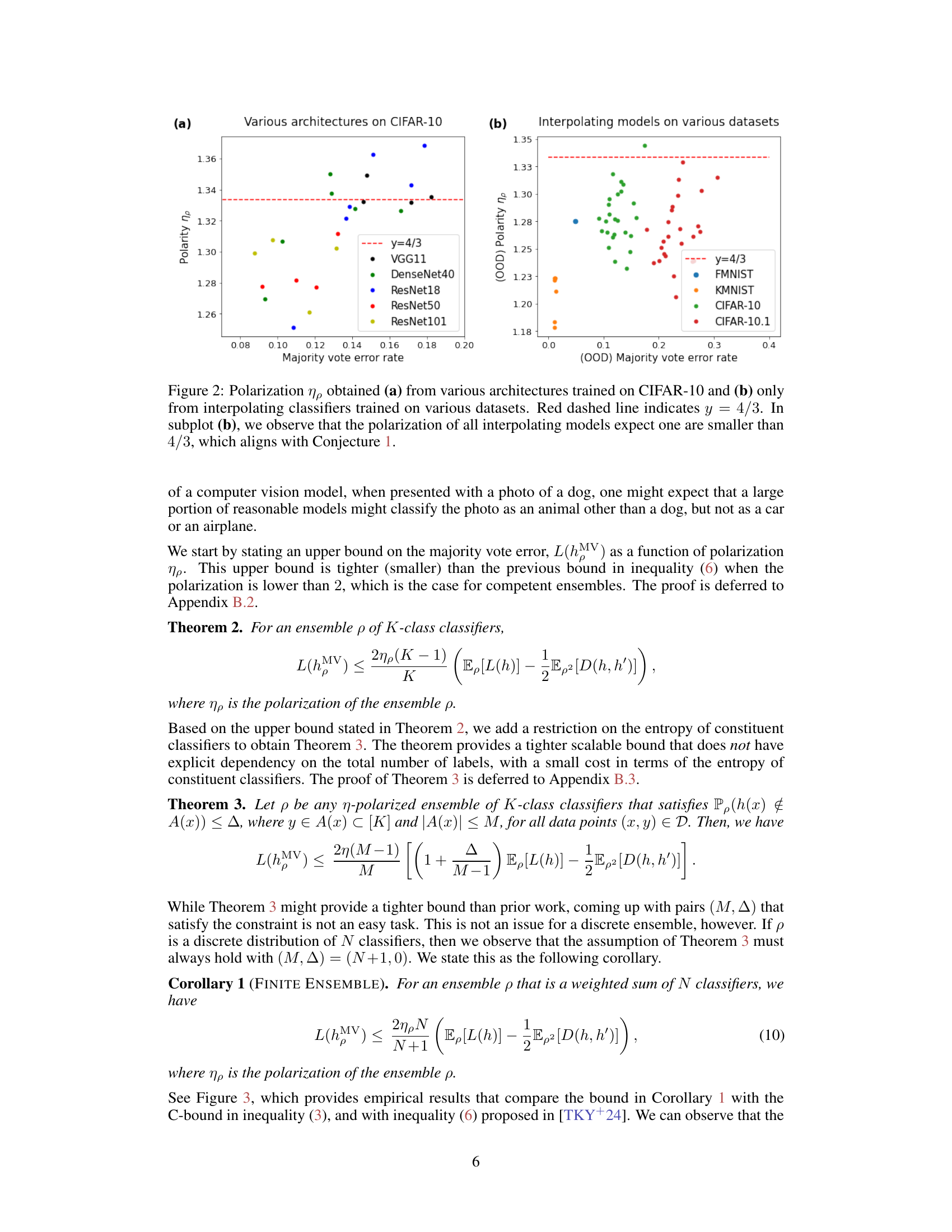
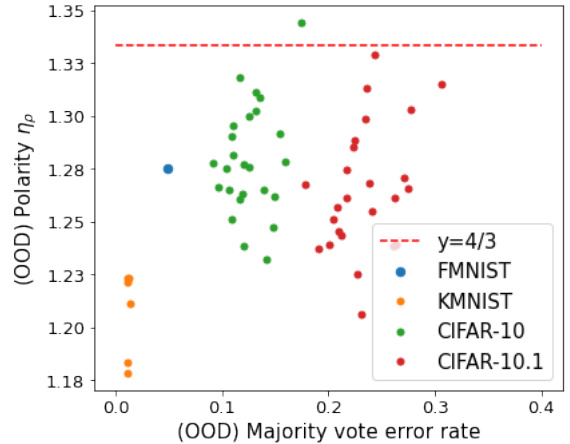
🔼 This figure visualizes the polarization (ηρ) of different ensemble models trained on various datasets. Subplot (a) shows the polarization for different neural network architectures trained on CIFAR-10, while subplot (b) focuses on interpolating models across various datasets. A red dashed line at y=4/3 is shown as a reference, representing the neural polarization law proposed in the paper. The figure supports the paper’s conjecture that most interpolating neural networks are 4/3-polarized, with the majority of points falling below this line.
read the caption
Figure 2: Polarization ηρ obtained (a) from various architectures trained on CIFAR-10 and (b) only from interpolating classifiers trained on various datasets. Red dashed line indicates y = 4/3. In subplot (b), we observe that the polarization of all interpolating models expect one are smaller than 4/3, which aligns with Conjecture 1.
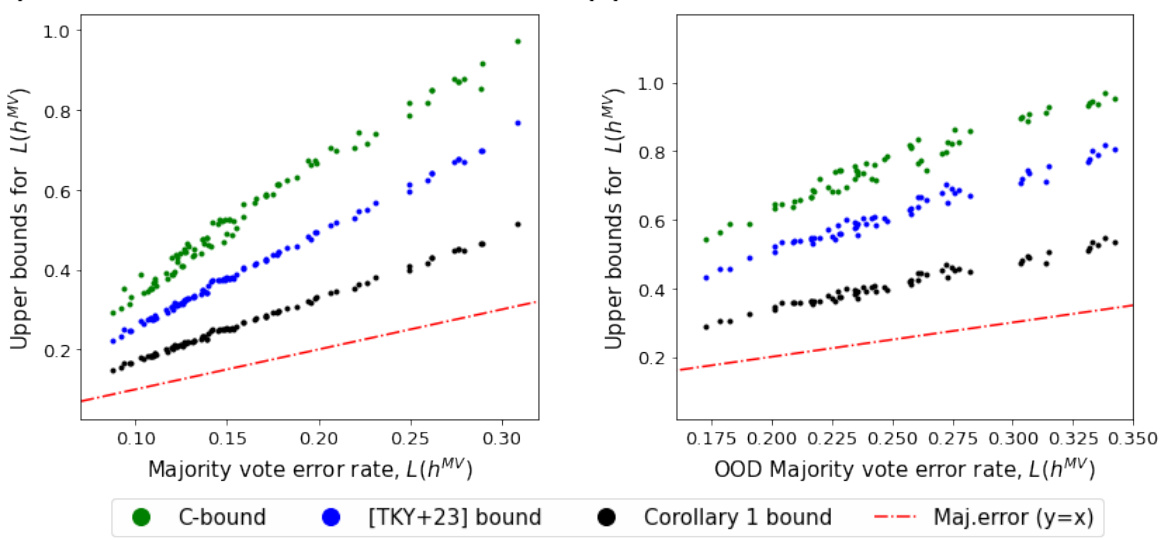
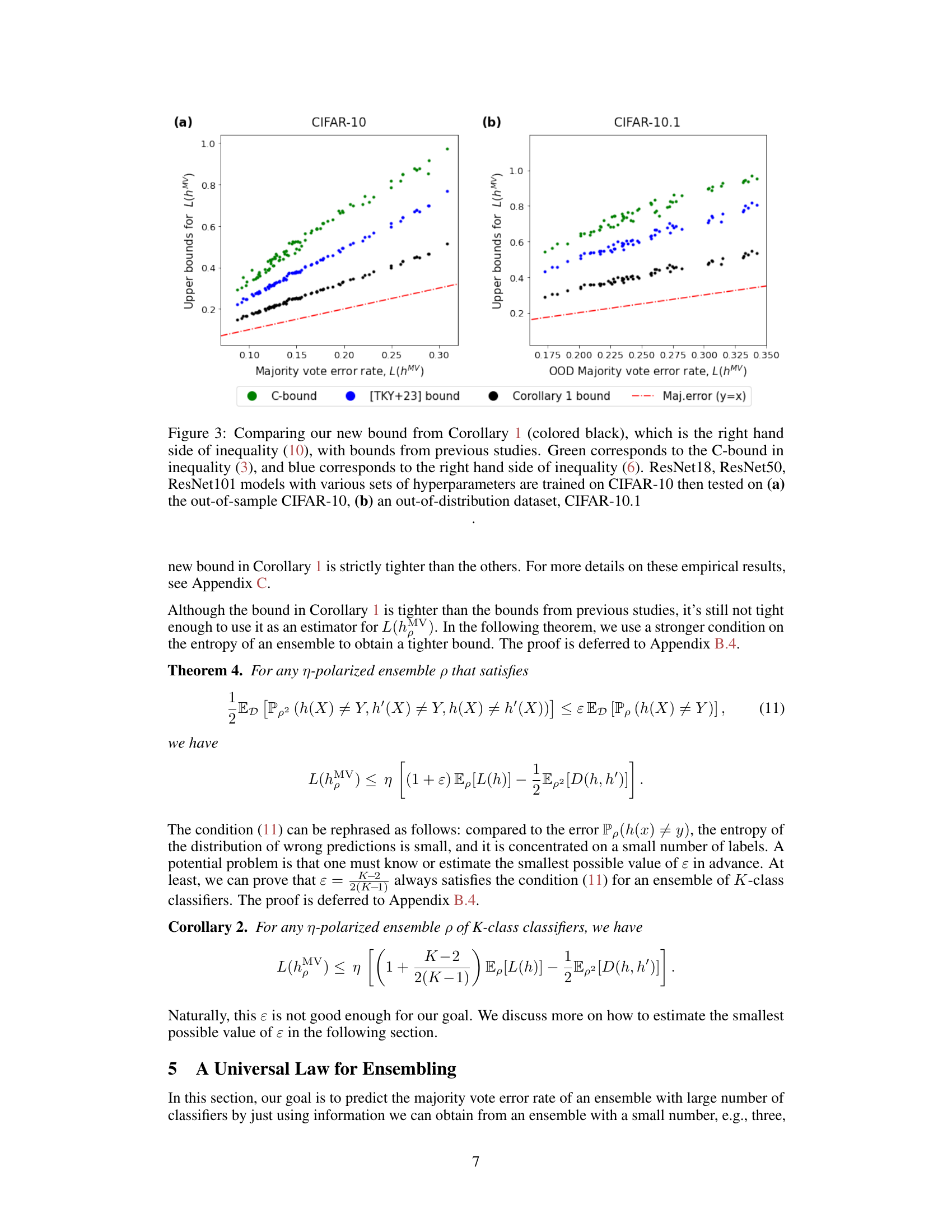
🔼 This figure compares the new bound on the majority vote error rate from Corollary 1 with existing bounds from previous works. The plot shows that the new bound is tighter than the previous bounds for both in-distribution (CIFAR-10) and out-of-distribution (CIFAR-10.1) datasets. Different ResNet models and hyperparameters were used, demonstrating the bound’s efficacy across various settings.
read the caption
Figure 3: Comparing our new bound from Corollary 1 (colored black), which is the right hand side of inequality (10), with bounds from previous studies. Green corresponds to the C-bound in inequality (3), and blue corresponds to the right hand side of inequality (6). ResNet18, ResNet50, ResNet101 models with various sets of hyperparameters are trained on CIFAR-10 then tested on (a) the out-of-sample CIFAR-10, (b) an out-of-distribution dataset, CIFAR-10.1
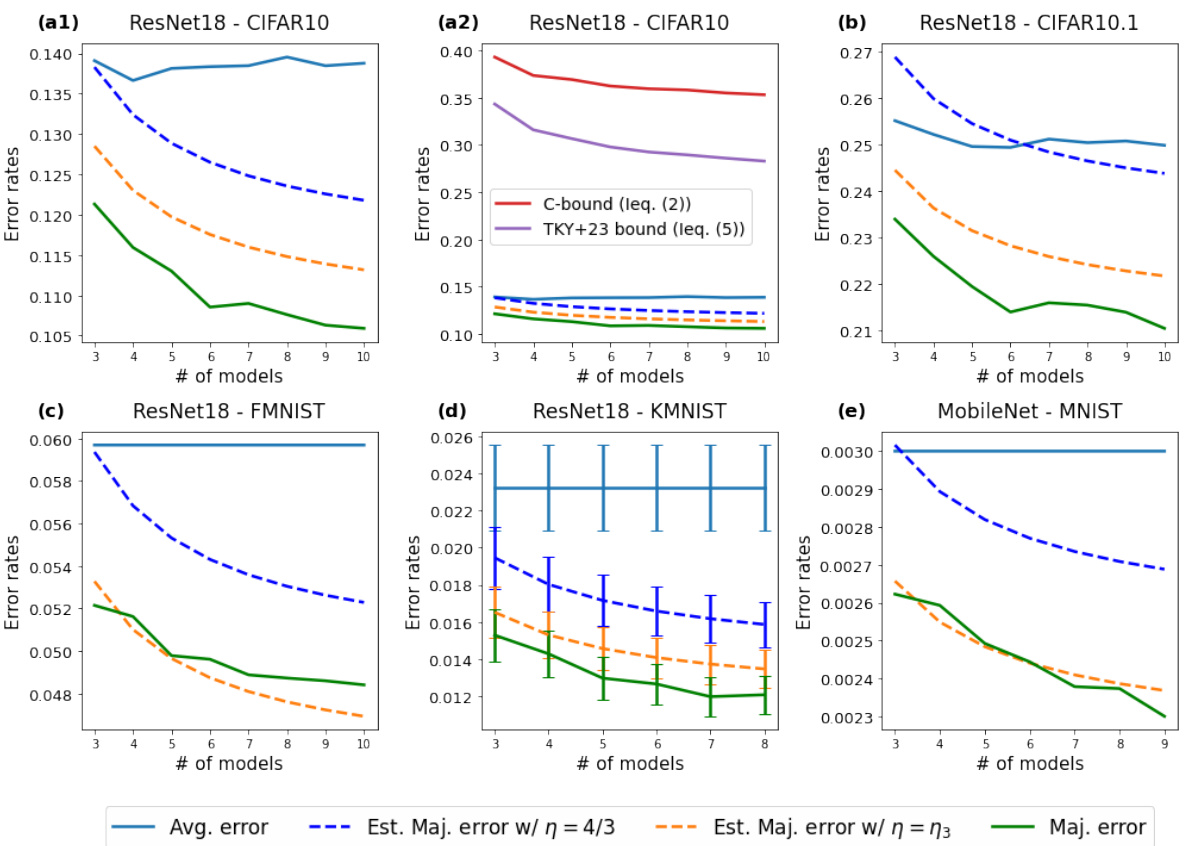
🔼 This figure compares the new upper bound on the majority vote error rate derived in Corollary 1 with existing bounds from previous studies. It shows the majority vote error rate against different upper bounds for two datasets: CIFAR-10 (in-distribution) and CIFAR-10.1 (out-of-distribution). ResNet18, ResNet50, and ResNet101 models with varying hyperparameters were used. The plot demonstrates that the new bound (black line) provides a tighter estimation of the majority vote error rate compared to previous bounds (green and blue lines).
read the caption
Figure 3: Comparing our new bound from Corollary 1 (colored black), which is the right hand side of inequality (10), with bounds from previous studies. Green corresponds to the C-bound in inequality (3), and blue corresponds to the right hand side of inequality (6). ResNet18, ResNet50, ResNet101 models with various sets of hyperparameters are trained on CIFAR-10 then tested on (a) the out-of-sample CIFAR-10, (b) an out-of-distribution dataset, CIFAR-10.1
Full paper#