TL;DR#
Generating realistic and structured multi-track music accompaniment from simple input, like a lead sheet, is a challenging task in music AI. Existing methods often struggle with maintaining track cohesion, ensuring long-term coherence, and optimizing computational efficiency. This often results in arrangements that lack musical coherence or are computationally expensive to produce. This paper addresses these challenges by leveraging prior modeling over disentangled style factors.
The proposed method uses a two-stage process: first, it generates a piano arrangement, and second, it orchestrates this arrangement into a multi-track score. A unique multi-stream Transformer architecture is used to model the long-term flow of orchestration styles, allowing for flexible, controllable, and structured music generation. Experiments demonstrate that this approach significantly outperforms existing baselines in terms of coherence, structure, and overall arrangement quality, while also improving computational efficiency. The system also supports a variety of music genres and allows for style control at different levels.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to multi-track accompaniment arrangement, a crucial task in music AI. The proposed method enhances generative capacity, improves efficiency, and offers superior coherence and structure compared to existing methods. This opens avenues for further research in controllable music generation and representation learning, particularly in the context of long-term sequence modeling.
Visual Insights#
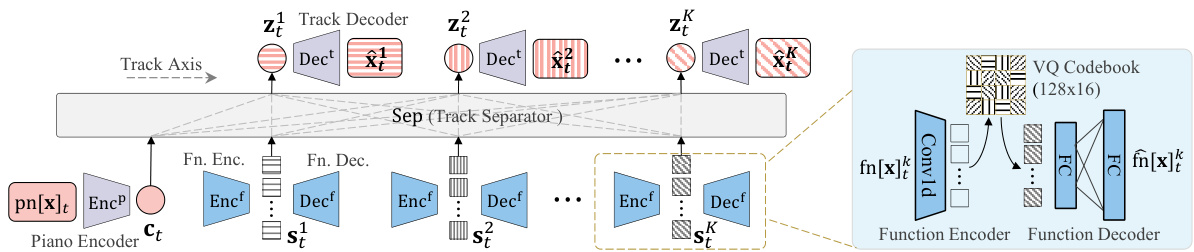
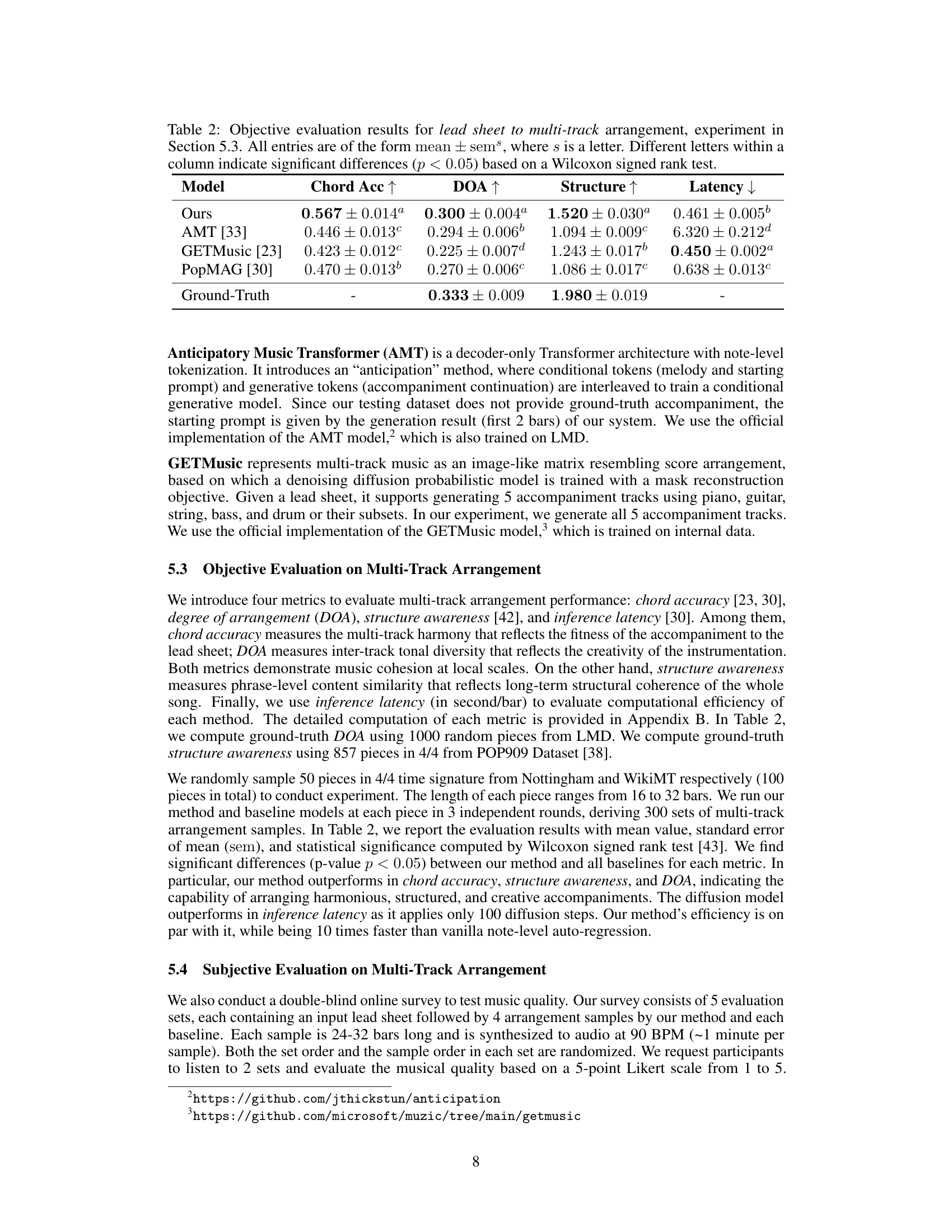
🔼 The figure illustrates the autoencoder architecture used in the paper. It consists of two main components: a VQ-VAE module (for encoding the orchestral function) and a VAE module (for encoding the piano reduction and reconstructing individual tracks). The VQ-VAE encodes orchestral functions into discrete embeddings using vector quantization. The VAE encodes the piano reduction and uses both the piano reduction content and the orchestral function style to reconstruct individual tracks. The Track Separator, a Transformer encoder, combines the style and content representations to generate each individual track’s representation.
read the caption
Figure 1: The autoencoder architecture. It learns content representation ct from piano reduction, style representations s1:K from orchestral function, and leverages both to reconstruct individual tracks.

🔼 This table summarizes the data representation used in the paper for three key elements: Multi-Track Arrangement, Piano Reduction, and Orchestral Function. It shows the data type and dimensions for each element, including the range of values for each dimension. Understanding this table is crucial to grasping the data processing steps within the proposed model.
read the caption
Table 1: Summary of the data representations applied in this paper. We use notation [a..b] to denote the integer interval {x | a ≤ x ≤ b, x ∈ Z} including both endpoints.
In-depth insights#
Style Prior Modeling#
Style prior modeling, in the context of music generation, presents a powerful approach to achieving long-term coherence and controllability in multi-track accompaniment arrangement. By modeling the probability distribution of style factors given content factors (like a piano reduction), this method overcomes the limitations of manually specifying styles or relying on simple heuristics. This allows for flexible and nuanced control over different musical aspects, including instrumentation, rhythm, and overall structure, across various musical genres. The approach is particularly valuable for generating structured, multi-track arrangements from simpler inputs, such as lead sheets, ensuring that the generated music maintains a sense of stylistic unity and musical plausibility. Disentangling content and style factors is crucial for this process, allowing for independent manipulation and refinement of each. This approach is also computationally advantageous due to its modularity, which enables more efficient generation and improved flexibility. The use of vector quantization and multi-stream transformers further enhances the model’s ability to capture both short-term and long-term musical dependencies.
Multi-stream Transformer#
A multi-stream Transformer architecture processes multiple sequential inputs simultaneously, unlike standard Transformers that handle single sequences. Its key advantage lies in its ability to model relationships and dependencies across different streams, allowing for the joint generation or analysis of multi-track music. The model likely employs a mechanism to interleave or combine the processing of different streams, maybe using shared attention layers or a combination of time-wise and track-wise layers to manage the computational complexity. This approach is particularly effective when dealing with data that inherently exhibits multi-stream characteristics, such as multi-track music which has different instruments playing simultaneously. The model’s effectiveness would depend on how it efficiently manages the interactions between streams while maintaining interpretability, enabling flexible control over the generated output (instruments, arrangement). The architecture’s success hinges on its ability to capture long-range dependencies within and between streams, a challenging task that requires carefully designed attention mechanisms and possibly specialized layer configurations. Ultimately, the core strength of the approach is its ability to address the inherent parallelism of multi-track music composition and analysis, leading to potentially improved coherence and naturalness in the generated output.
Two-Stage Approach#
A two-stage approach to multi-track accompaniment arrangement offers a structured and efficient solution. The first stage focuses on deriving a piano arrangement from a lead sheet, leveraging existing techniques in piano texture style transfer and representation learning. This stage establishes the fundamental harmonic and melodic structure, acting as a foundation for the subsequent orchestration. The second stage utilizes a novel style prior model to orchestrate the piano arrangement into a multi-track score. This model disentangles style factors from content, enabling flexible control over instrumentation and arrangement details. By factorizing the complex task into interpretable sub-problems, a two-stage approach enhances overall arrangement quality, improves computational efficiency, and facilitates flexible control over various musical aspects. This modular design is particularly powerful, allowing for independent optimization and refinement of each stage, leading to a more robust and controllable system. The approach also offers the advantage of interpretability, allowing for a clearer understanding of the arrangement process at each level. Improved coherence and long-term structure are also key benefits compared to single-stage approaches. However, a potential limitation is the possibility of error propagation between stages; mistakes in the first stage could negatively impact the second.
Ablation Study#
An ablation study systematically removes components of a model to determine their individual contributions. In this context, it would likely involve removing or altering aspects of the style prior modeling, such as the multi-stream Transformer architecture or vector quantization, to assess their impact on overall model performance. Key insights would emerge from comparing the performance of the full model against these variants. For example, removing the style prior might lead to less coherent or less stylistically consistent outputs, indicating the importance of this component. Similarly, altering the architecture or quantization methods might reveal tradeoffs between computational efficiency and the quality of the generated music. The results would help to validate design choices and potentially reveal which aspects of the system are most critical for achieving high-quality, structured multi-track accompaniment. Such a study is vital in evaluating the effectiveness of the proposed system, isolating critical parts, and justifying design decisions.
Musicality & Cohesion#
Musicality and cohesion are paramount in evaluating the quality of music generation. Musicality encompasses the inherent aesthetic appeal of the generated music, judging aspects like melody, harmony, rhythm, and overall emotional impact. A musically satisfying piece will feel natural and expressive, engaging the listener on an emotional level. Cohesion, on the other hand, refers to the internal consistency and structural integrity of the composition. A cohesive piece seamlessly integrates its various sections, creating a unified and coherent whole. In multi-track arrangements, cohesion is particularly crucial, as each individual track must work together harmoniously to contribute to the overall musical effect. The successful generation of music thus depends on a delicate balance between musicality and cohesion. A piece might be musically brilliant but lack structural coherence, leading to an unsatisfying listening experience. Conversely, it can be structurally sound but lack the expressiveness and emotional depth to truly resonate. Therefore, assessing both aspects is vital for evaluating the overall artistic merit of generated music.
More visual insights#
More on figures

🔼 This figure illustrates the architecture of the style prior model used in the paper. The model is an encoder-decoder transformer that takes piano reduction as input and outputs orchestral functions. The decoder is designed with interleaved time-wise and track-wise layers to model dependencies in both time and track directions. The time-wise layers handle long-term coherence, while the track-wise layers enable flexible control over instrumentation. The encoder processes the piano reduction to provide context for the decoder. Various embeddings (sinusoidal positional, relative positional, music timing, instrument) and Gaussian noise are added to enhance the model’s capacity. The arrows show the information flow between different components of the model.
read the caption
Figure 2: The prior model architecture. The overall architecture is an encoder-decoder Transformer, while the decoder module is interleaved with orthogonal time-wise and track-wise layers.
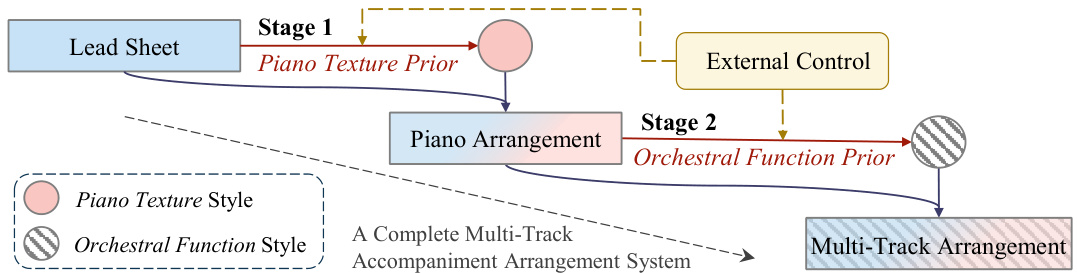
🔼 This figure illustrates the two-stage system for multi-track accompaniment arrangement. Stage 1 uses a piano texture prior to generate a piano arrangement from a lead sheet. Stage 2 leverages an orchestral function prior, conditioned on the piano arrangement from Stage 1, to produce a final multi-track arrangement. External control can be applied at various stages. The system is modular, allowing for flexible control at both the piano texture and orchestral function levels.
read the caption
Figure 3: A complete accompaniment arrangement system based on cascaded prior modelling. The first stage models piano texture style given lead sheet while the second stage models orchestral function style given piano. Besides modularity, the system offers control on both composition levels.

🔼 This figure displays a multi-track arrangement of the song ‘Can You Feel the Love Tonight.’ It highlights several key aspects of the model’s output: long-term coherence (red dotted boxes show consistent patterns across multiple bars), track cohesion (colored blocks illustrate the interplay between different instrument tracks, highlighting counterpoint, harmonic/melodic divisions, and metrical divisions), and the overall naturalness and quality of the arrangement. The arrangement includes multiple tracks (celesta, acoustic guitars, electric pianos, acoustic piano, violin, brass, electric bass).
read the caption
Figure 4: Arrangement for Can You Feel the Love Tonight, a pop song in a total of 60 bars. We show two chorus parts from bar 13 to 41. We use red dotted boxes to show coherence in long-term structure. We use coloured blocks to show naturalness and cohesion in multi-track arrangement.

🔼 This figure presents the results of a subjective evaluation of the lead sheet to multi-track arrangement task. The evaluation was performed using a 5-point Likert scale across five criteria: Harmony and Texture Coherency, Long-Term Structure, Naturalness, Creativity, and Overall Musicality. The chart displays the mean ratings and standard errors for the authors’ model and three baseline models (AMT, GETMusic, PopMAG). The results demonstrate the superior performance of the authors’ model across all criteria.
read the caption
Figure 5: Subjective evaluation results on lead sheet to multi-track arrangement (Section 5.4).
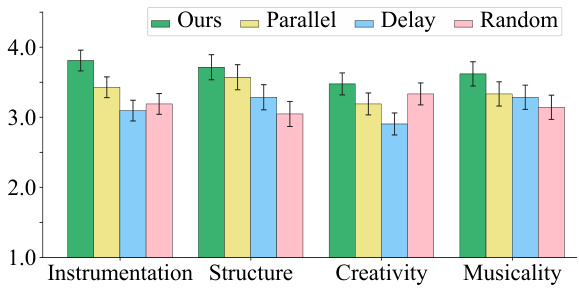
🔼 This figure presents the results of a subjective evaluation of piano to multi-track arrangement. The evaluation involved human listeners rating four different models (Ours, Parallel, Delay, and Random) on five criteria: Instrumentation, Structure, Creativity, Musicality. Each bar represents the average rating for a specific model on a criterion, with error bars indicating the standard error. The figure visually compares the perceived quality of the arrangements produced by each model, allowing for a qualitative assessment of their strengths and weaknesses regarding these specific aspects of musical composition. The section in the paper this figure belongs to discusses the ablation study on different style prior architectures.
read the caption
Figure 6: Subjective evaluation results on piano to multi-track arrangement (Section 5.5).
🔼 This figure illustrates the architecture of the autoencoder used in the paper. The autoencoder takes as input both piano reduction (content) and orchestral function (style). The piano reduction is encoded into a content representation ct via a variational autoencoder (VAE). Simultaneously, the orchestral function is encoded into style representations s1:K (one for each track) via a vector quantized variational autoencoder (VQ-VAE). A track separator combines these content and style representations to reconstruct the individual tracks. This process disentangles content and style information, allowing for more flexible and controllable music generation.
read the caption
Figure 1: The autoencoder architecture. It learns content representation ct from piano reduction, style representations s1:K from orchestral function, and leverages both to reconstruct individual tracks.

🔼 This figure shows a multi-track arrangement of the song ‘Can You Feel the Love Tonight.’ The arrangement includes multiple instrument tracks (melody, acoustic guitars, electric pianos, violin, brass, electric bass, etc.) and highlights several aspects: * Long-term coherence: Red dotted boxes illustrate how the arrangement maintains a consistent musical idea across a significant portion of the song (over 30 bars). * Track cohesion: Colored blocks demonstrate how different tracks work together naturally, creating a coherent and musically pleasing texture. Specific relationships are pointed out such as counterpoint between guitar and piano, complementary rhythmic functions between guitar tracks, and the metrical division between strings and brass. * Multi-track structure: The arrangement demonstrates a typical structure in multi-track music, such as distinct instrumental voicing that provides interesting textures, harmonic and melodic divisions between instrument groups, and consistent arrangement patterns across multiple sections of a piece.
read the caption
Figure 4: Arrangement for Can You Feel the Love Tonight, a pop song in a total of 60 bars. We show two chorus parts from bar 13 to 41. We use red dotted boxes to show coherence in long-term structure. We use coloured blocks to show naturalness and cohesion in multi-track arrangement.

🔼 This figure shows the lead sheet for the song ‘Can You Feel the Love Tonight.’ A lead sheet is a simplified musical notation showing only the melody line and basic chord changes. It’s often used by musicians as a starting point for arranging a more complete musical score. The lead sheet in this figure shows the song’s structure in terms of sections: Intro (i4), verses (A8), choruses (B8), and an interlude (x4), and an outro (04). This simplified structure is then used as input to the proposed system in the paper to generate a full multi-track arrangement. The number of bars in the song is also indicated.
read the caption
Figure 8: Lead sheet for pop song Can You Feel the Love Tonight.

🔼 This figure illustrates the two-stage process for accompaniment arrangement using cascaded prior modelling. Stage 1 uses a piano texture prior to generate a piano arrangement from a lead sheet. The output of stage 1 is then used as input to stage 2, which uses an orchestral function prior to generate a multi-track arrangement. The system allows for control over both texture style (stage 1) and orchestral function style (stage 2).
read the caption
Figure 3: A complete accompaniment arrangement system based on cascaded prior modelling. The first stage models piano texture style given lead sheet while the second stage models orchestral function style given piano. Besides modularity, the system offers control on both composition levels.

🔼 This figure illustrates the two-stage system for accompaniment arrangement. The first stage uses a piano texture prior to generate a piano arrangement from a lead sheet. The second stage uses an orchestral function prior to orchestrate the piano arrangement into a multi-track arrangement. This modular design allows for control at both the piano texture and orchestral function levels.
read the caption
Figure 3: A complete accompaniment arrangement system based on cascaded prior modelling. The first stage models piano texture style given lead sheet while the second stage models orchestral function style given piano. Besides modularity, the system offers control on both composition levels.

🔼 This figure displays a multi-track arrangement of the song ‘Can You Feel the Love Tonight,’ focusing on two chorus sections (bars 13-41). Red dotted boxes highlight the long-term coherence of the arrangement. Colored blocks illustrate specific musical relationships and cohesion between different tracks (e.g., counterpoint, harmonic division). The image demonstrates the system’s ability to generate a multi-track arrangement with both short-term cohesion and long-term coherence, showcasing the results of the proposed approach.
read the caption
Figure 4: Arrangement for Can You Feel the Love Tonight, a pop song in a total of 60 bars. We show two chorus parts from bar 13 to 41. We use red dotted boxes to show coherence in long-term structure. We use coloured blocks to show naturalness and cohesion in multi-track arrangement.

🔼 This figure shows a multi-track arrangement of the song ‘Can You Feel the Love Tonight.’ The arrangement spans 60 bars, with this image focusing on bars 13-41, showing two choruses. Red boxes highlight the long-term coherence and structural alignment across the arrangement. Colored blocks illustrate specific musical relationships between different instrument tracks, such as counterpoint, harmonic layering, and rhythmic interplay. The image demonstrates the system’s ability to generate a cohesive and natural-sounding multi-track arrangement with clear structural organization and stylistic coherence.
read the caption
Figure 4: Arrangement for Can You Feel the Love Tonight, a pop song in a total of 60 bars. We show two chorus parts from bar 13 to 41. We use red dotted boxes to show coherence in long-term structure. We use coloured blocks to show naturalness and cohesion in multi-track arrangement.

🔼 This figure shows the first page of the multi-track arrangement generated by the proposed system for the song ‘Can You Feel the Love Tonight’. The arrangement includes nine tracks: Melody, Celesta, Acoustic Guitar 1, Acoustic Guitar 2, Piano, Electric Piano 1, Electric Piano 2, Violins, Brass, and Electric Bass. The musical notation shows the melody line and the accompaniment parts for each instrument in the different sections of the song. The figure demonstrates the system’s ability to generate complex and coherent multi-track arrangements based on a given lead sheet. The specific instrumentation was chosen to showcase the model’s flexibility in handling various instruments. The arrangement demonstrates the system’s ability to generate coherent multi-track arrangements with a flexible number of tracks and a wide range of instrument choices.
read the caption
Figure 11: Multi-track arrangement score (page 1).

🔼 This figure displays a multi-track arrangement of the song ‘Can You Feel the Love Tonight,’ focusing on bars 13-41, which include two choruses. Red dotted boxes highlight the long-term coherence across different sections. Colored blocks illustrate how different instrumental tracks (e.g., acoustic guitars, electric piano, strings, brass) interact, demonstrating a natural and cohesive multi-track arrangement.
read the caption
Figure 4: Arrangement for Can You Feel the Love Tonight, a pop song in a total of 60 bars. We show two chorus parts from bar 13 to 41. We use red dotted boxes to show coherence in long-term structure. We use coloured blocks to show naturalness and cohesion in multi-track arrangement.

🔼 This figure shows the first page of a multi-track arrangement generated by the system for the song ‘Can You Feel the Love Tonight.’ It displays the melody and the arrangement for nine different instruments across the bars. The instruments include celesta, acoustic guitars (two), electric pianos (two), acoustic piano, violins, brass, and electric bass. The arrangement demonstrates the model’s ability to generate a structured, multi-track accompaniment maintaining coherence.
read the caption
Figure 11: Multi-track arrangement score (page 1).

🔼 This figure shows the first page of a multi-track arrangement generated by the system for the song ‘Can You Feel the Love Tonight’. The arrangement includes multiple instrument tracks, such as celesta, acoustic guitars, electric pianos, violin, brass, and electric bass, showcasing the system’s ability to generate structured and nuanced multi-track music from a piano reduction.
read the caption
Figure 11: Multi-track arrangement score (page 1).
More on tables

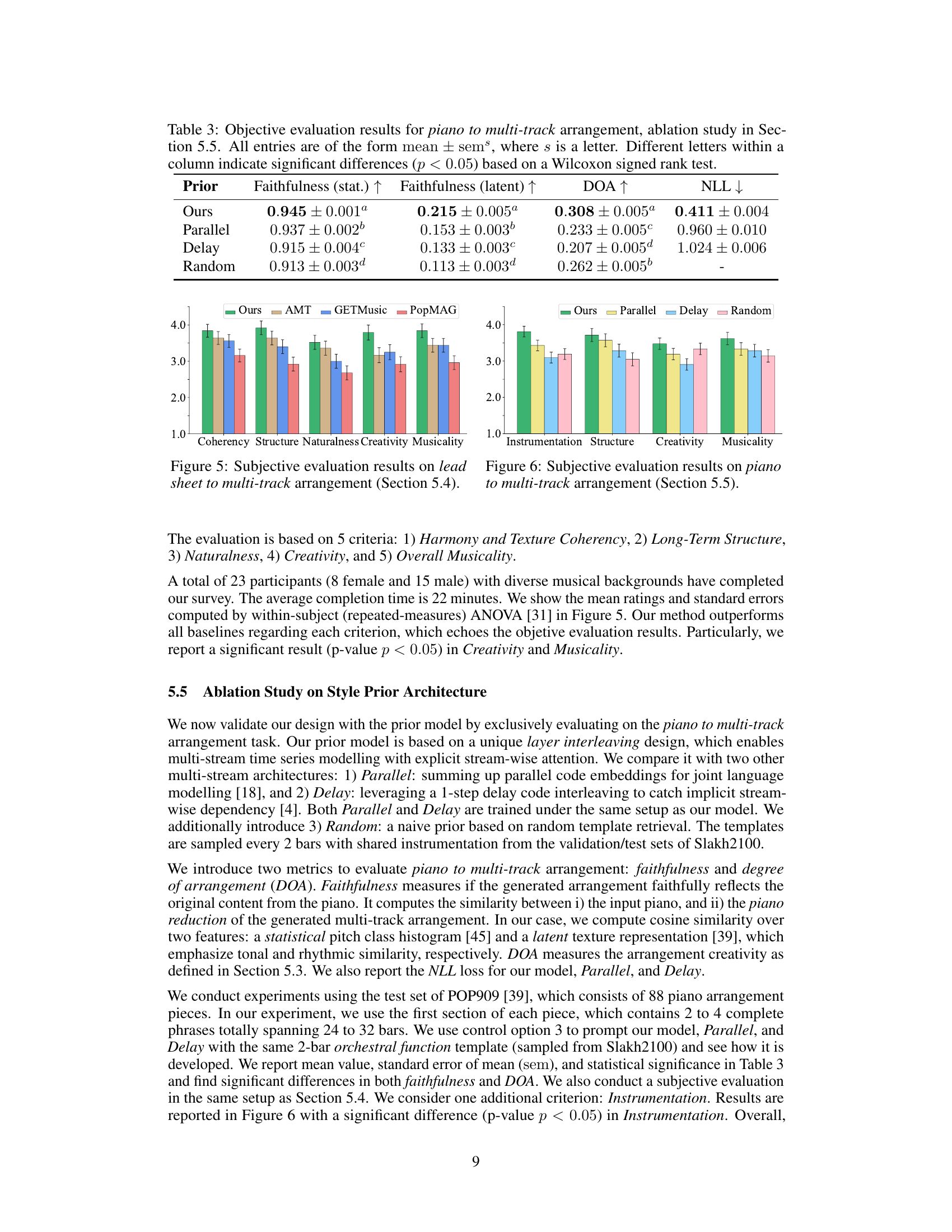
🔼 This table presents the objective evaluation results of different models on the task of lead sheet to multi-track accompaniment arrangement. The metrics used are Chord Accuracy (measuring the harmony of the accompaniment), Degree of Arrangement (measuring the creativity and diversity of instrumentation), Structure Awareness (measuring the long-term coherence of the arrangement), and Latency (measuring the computational efficiency). The results show the performance of the proposed model compared to existing baselines, indicating the superior performance of the proposed method.
read the caption
Table 2: Objective evaluation results for lead sheet to multi-track arrangement, experiment in Section 5.3. All entries are of the form mean ± sem³, where s is a letter. Different letters within a column indicate significant differences (p < 0.05) based on a Wilcoxon signed rank test.

🔼 This table presents the objective evaluation results of an ablation study on the style prior architecture for piano to multi-track arrangement. It compares four different prior models: Ours (the proposed model), Parallel, Delay, and Random. The evaluation metrics include Faithfulness (statistical), Faithfulness (latent), Degree of Arrangement (DOA), and Negative Log-Likelihood (NLL). Statistically significant differences (p<0.05) between models are indicated by different letters within each column.
read the caption
Table 3: Objective evaluation results for piano to multi-track arrangement, ablation study in Section 5.5. All entries are of the form mean ± sems, where s is a letter. Different letters within a column indicate significant differences (p < 0.05) based on a Wilcoxon signed rank test.

🔼 This table presents the results of an ablation study comparing two different methods for the first stage of a two-stage multi-track accompaniment arrangement system. The first stage involves generating a piano accompaniment from a lead sheet, and the second stage orchestrates the piano accompaniment into a multi-track arrangement. The table compares the performance of the proposed system’s piano arrangement method against an alternative method, focusing on three key metrics: Chord Accuracy (how well the harmony of the generated accompaniment matches the lead sheet), Structure (the quality of the overall arrangement’s long-term structure), and Degree of Arrangement (the creativity and diversity of instrumentation in the multi-track arrangement). The results show that using the proposed system’s method for piano arrangement leads to significantly better performance on all three metrics in the final multi-track arrangement.
read the caption
Table 4: Ablation study on alternative lead sheet to piano arrangement (Stage 1) modules, experiment in Section 5.6. Here we investigate the impact of Stage 1 to the entire two-stage system. Evaluation results are based on the final multi-track arrangement (using respective Stage 1 modules).

🔼 This table presents the results of an objective evaluation comparing two methods for lead sheet to piano accompaniment generation. The ‘Chord Acc’ metric assesses the accuracy of the generated piano accompaniment’s chord progression against the ground truth. The ‘Structure’ metric evaluates the structural coherence of the generated piano accompaniment. The comparison is between the proposed method (using a Piano Texture Prior) and a baseline method (Whole-Song-Gen [42]). The results indicate the superior performance of the proposed Piano Texture Prior approach on both metrics.
read the caption
Table 5: Objective evaluation on the exclusive task of lead sheet to piano arrangement, experiment in Section 5.6. Evaluation results are based on the direct output of Stage 1 (i.e., piano accompaniment).

🔼 This table shows the results of an experiment on the impact of noise weight (γ) on the model’s performance in terms of faithfulness and degree of arrangement (DOA). Different values of γ were tested, ranging from 0 to 1. The results show a trade-off between faithfulness (how well the generated arrangement reflects the input piano) and DOA (the creativity and diversity of the arrangement). Higher γ values lead to more creative arrangements but at the cost of faithfulness, and vice versa.
read the caption
Table 6: The impact of noise weight γ, experiment in Appendix C.
Full paper#