Building a stable classifier with the inflated argmax

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel framework for algorithmic stability in multiclass classification, a critical issue in machine learning. It offers a provable stability guarantee without distributional assumptions, addressing a significant limitation of existing methods. The inflated argmax method and its efficiency are also significant contributions, opening up new avenues for research in developing robust and reliable classifiers.

Visual Insights

#

🔼 This figure visualizes the inflated argmax and standard argmax on a 3D simplex (triangle). The left plot shows how the inflated argmax assigns regions of the simplex to different sets of candidate labels, illustrating its insensitivity to small probability changes. The right plot depicts the standard argmax for comparison. This highlights how the inflated argmax is a stable alternative to the standard argmax.

read the caption

Figure 1: The left plot illustrates the inflated argmax (1) over the simplex ∆L−1 when L = 3. The numbers in brackets correspond to the output of the inflated argmax, argmax(w), for various points w in the simplex. The right plot shows the same but for the standard argmax, which corresponds to the limit of argmax(w) as ɛ → 0.

🔼 This table presents results on the Fashion MNIST data set, comparing four different methods for multiclass classification: argmax, inflated argmax, bagged argmax, and bagged inflated argmax. The table shows the frequency of each method returning the correct label as a singleton, the average size of the returned sets of labels, and a measure of the worst-case instability of the method.

read the caption

Table 1: Results on the Fashion MNIST data set. We display the frequency of returning the correct label as a singleton, Bcorrect-single and the average size, Bset-size, both of which are defined in (6). Standard errors for these averages are shown in parentheses. The final column shows the worst-case instability over the test set, Bmax-instability, defined in (5). For each metric, the symbol // indicates that higher values are desirable, while indicates that lower values are desirable.

In-depth insights

#

Inflated Argmax

#

The proposed “Inflated Argmax” offers a novel approach to enhance the stability of multiclass classifiers. Unlike the standard argmax, which is highly sensitive to small data perturbations, Inflated Argmax introduces a margin of error, allowing for a set of candidate labels rather than a single prediction. This relaxation of argmax directly addresses the inherent instability of the standard method by incorporating a measure of uncertainty. The resulting classifier is provably stable under mild conditions, placing no distributional assumptions on the data. Efficiency is ensured by developing an algorithm to efficiently compute the inflated argmax, mitigating concerns about computational cost. The integration of bagging further improves stability. The inflated argmax’s effectiveness is empirically demonstrated, showcasing its ability to improve stability without compromising accuracy. The key benefit is its applicability to any base classifier, making it a versatile tool for various multiclass classification tasks.

Selection Stability

#

The concept of “Selection Stability” in the context of multiclass classification addresses a critical weakness in traditional approaches. Standard argmax, while efficient, is highly unstable, susceptible to minor data perturbations that drastically alter predictions. The authors introduce a novel framework, focusing on the stability of the final predicted labels, not just intermediate probability scores. This necessitates a move towards set-valued classifiers, accepting a set of possible labels instead of a single prediction. The key innovation is the “inflated argmax,” a stable relaxation of the standard argmax. This modification provides a provable stability guarantee, irrespective of data distribution, dimensionality, or the number of classes. By integrating bagging, the authors achieve a completely assumption-free stable classification pipeline. The inflated argmax elegantly handles ambiguous cases, yielding smaller sets of predictions when confidence is high, and larger sets otherwise, adapting to data uncertainty. This approach provides a principled balance between stability and accuracy, directly addressing practical concerns about model reliability and trustworthiness.

Bagging’s Role

#

Bagging, or bootstrap aggregating, plays a crucial role in stabilizing the classification process by reducing the variance of the base classifier’s predictions. Its core function is to create multiple versions of the base classifier by training them on different subsets of the training data. This is achieved through random sampling with replacement, resulting in a collection of classifiers that capture various aspects of the training data. Averaging the predictions from these diverse classifiers enhances the model’s robustness to noise and outliers. The inflated argmax, as a post-processing step, further mitigates instability by selecting a set of plausible labels instead of a single prediction. Bagging’s effectiveness stems from its ability to create a more generalized, less prone to overfitting classifier which translates to increased stability in the face of small data perturbations. The stability guarantee derived from using bagging and the inflated argmax is particularly powerful because it is assumption free—it makes no distributional assumptions about the data, which is critical for real-world applicability.

Empirical Analysis

#

An Empirical Analysis section in a research paper would typically present the results of experiments designed to test the hypotheses or claims made earlier. A strong analysis would begin by clearly stating the experimental design, including the datasets used, the metrics employed, and the statistical methods for assessing significance. It’s crucial to present the results transparently, possibly with tables and figures to show the performance of different methods or models. Clear visualisations are key, making it easier to understand complex results. A thorough discussion should follow, explaining whether the findings support or refute the hypotheses, highlighting any unexpected results, and acknowledging any limitations or potential biases. Addressing limitations is vital; a good analysis will openly discuss aspects that could affect the reliability or generalizability of the findings. Finally, a connection back to the paper’s overall claims is necessary, summarizing the contributions made to the field. The section should strive to be objective and data-driven, avoiding subjective interpretations unless appropriately justified. A compelling empirical analysis demonstrates a clear understanding of the research, robust methodologies, and rigorous interpretation of results.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the inflated argmax to handle structured data beyond vectors would significantly broaden its applicability. Investigating the impact of different bagging methods and their interaction with the inflated argmax on stability and accuracy is crucial. A deeper theoretical analysis examining the optimal choice of ε for the inflated argmax under various data distributions would refine its practical implementation. Furthermore, a comparative study against other set-valued classification techniques focusing on both theoretical guarantees and empirical performance across diverse datasets would solidify its position within the field. Finally, developing efficient algorithms for computing the inflated argmax in high-dimensional settings is essential for practical application to large-scale problems.

More visual insights

#

More on figures

🔼 This figure visualizes the inflated argmax and standard argmax on a 3-dimensional simplex. The left plot shows how the inflated argmax produces a set of candidate labels based on the distance to the regions where a single label would be selected; the size of these regions is controlled by the inflation parameter ɛ. The right plot shows the standard argmax, which selects a single label based on the maximum probability. This illustrates how the inflated argmax is a smoother, more stable version of argmax.

read the caption

Figure 1: The left plot illustrates the inflated argmax (1) over the simplex ∆L−1 when L = 3. The numbers in brackets correspond to the output of the inflated argmax, argmax(w), for various points w in the simplex. The right plot shows the same but for the standard argmax, which corresponds to the limit of argmax(w) as ɛ → 0.

🔼 This figure shows a visualization of the inflated argmax and standard argmax functions on a 3-dimensional simplex (L=3). The left panel depicts the inflated argmax, illustrating how different regions of the simplex map to different sets of candidate labels. The size of the regions reflects the stability introduced by inflation. The right panel shows the standard argmax, highlighting its discontinuous and unstable nature. This comparison demonstrates how the inflated argmax provides a stable relaxation of the argmax.

read the caption

Figure 1: The left plot illustrates the inflated argmax (1) over the simplex ∆L−1 when L = 3. The numbers in brackets correspond to the output of the inflated argmax, argmax(w), for various points w in the simplex. The right plot shows the same but for the standard argmax, which corresponds to the limit of argmax(w) as ɛ → 0.

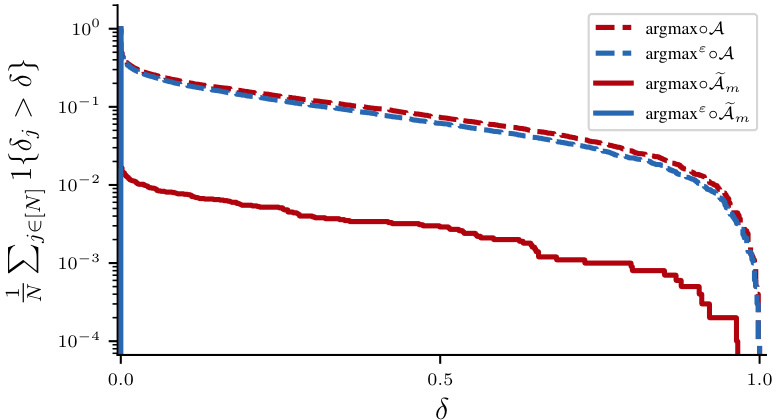
🔼 This figure compares the instability of four different classification methods on the Fashion MNIST dataset. The instability (δj) measures how much the predicted label changes when a single data point is removed from the training set. The plot shows, for each method, the fraction of test points whose instability exceeds a given threshold (δ). Lower curves indicate greater stability. The methods compared are standard argmax, inflated argmax (both applied to the base classifier) and standard and inflated argmax applied to a bagged version of the base classifier. The results show that using a bagged classifier and the inflated argmax produces a significantly more stable classifier.

read the caption

Figure 2: Results on the Fashion MNIST data set. The figure shows the instability δj (defined in (4)) over all test points j = 1, . . ., N. The curves display the fraction of δj's that exceed δ, for each value δ ∈ [0, 1]. The vertical axis is on a log scale. See Section 4 for details.

🔼 This figure visualizes the inflated argmax (left) and standard argmax (right) operators on a 3-dimensional probability simplex (L=3). The simplex represents all possible probability distributions over three classes. Each region in the plots is colored differently to indicate the subset of labels returned by each operator for points in that region. The inflated argmax is a smoothed version of the standard argmax, which is shown as the limit of the inflated argmax as the smoothing parameter goes to zero. The inflated argmax is designed to produce more stable label assignments when the probability scores are close.

read the caption

Figure 1: The left plot illustrates the inflated argmax (1) over the simplex ∆L−1 when L = 3. The numbers in brackets correspond to the output of the inflated argmax, argmax(w), for various points w in the simplex. The right plot shows the same but for the standard argmax, which corresponds to the limit of argmax(w) as ɛ → 0.

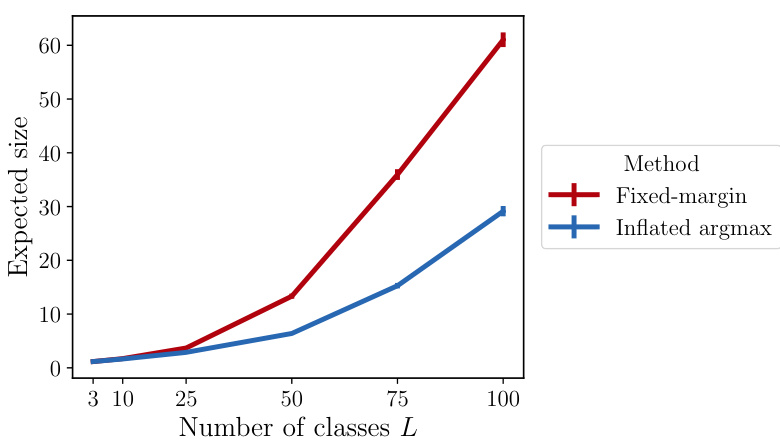
🔼 This figure compares the average set sizes of argmax and the fixed-margin selection rule for various values of L (number of classes). The plot shows that, as L increases, the average size of argmax stays consistently smaller than that of the fixed-margin rule. The difference is more pronounced for larger L, illustrating the efficiency gain of inflated argmax in higher dimensions.

read the caption

Figure 4: Simulation to compare the selection rules argmax and smargin. The figure shows the average set size, |argmax(w)| and |smargin(w)|, averaged over 1,000 random draws of w (with standard error bars shown). See Appendix D.2 for details.

Full paper

#