TL;DR#
Current gradient descent analysis often relies on global smoothness assumptions which can lead to pessimistic convergence rates that don’t reflect real-world optimization behavior. The limitations of existing methods are evident in their failure to predict optimization speed accurately. This makes it hard to devise efficient and adaptive algorithms.
This paper introduces the concept of directional smoothness, a measure of how much the gradient changes along specific directions. Using directional smoothness, the authors develop new suboptimality bounds for gradient descent (GD) that depend on the optimization path, providing tighter guarantees. They also show that classical step-size methods like the Polyak step-size implicitly adapt to directional smoothness, resulting in faster convergence than predicted by traditional theory. The findings are supported by experiments demonstrating the improved convergence of adaptive step-sizes compared to standard methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges conventional wisdom in gradient descent analysis by introducing the concept of directional smoothness. This allows for tighter convergence guarantees and opens avenues for developing more efficient and adaptive optimization algorithms.
Visual Insights#
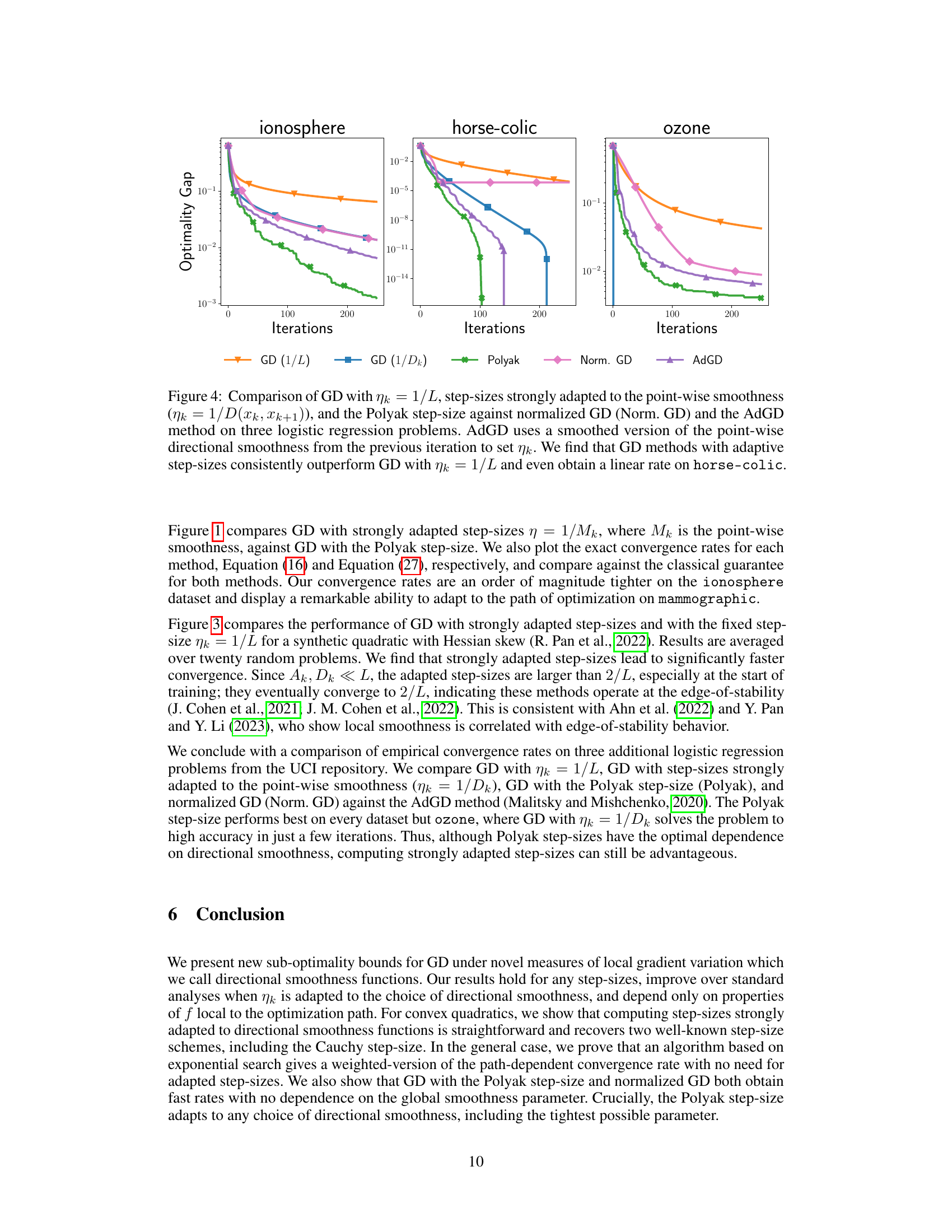
🔼 The figure compares the actual and theoretical convergence rates of gradient descent (GD) on two logistic regression datasets. It contrasts GD with step sizes adapted to directional smoothness (a measure of gradient variation along the optimization path) against GD using the Polyak step size. The results demonstrate that bounds derived using directional smoothness are tighter than those based on global L-smoothness and adapt better to the optimization path.
read the caption
Figure 1: Comparison of actual (solid lines) and theoretical (dashed lines) convergence rates for GD with (i) step-sizes strongly adapted to the directional smoothness (ηκ = 1/M(xk+1, xk)) and (ii) the Polyak step-size. Both problems are logistic regressions on UCI repository datasets (Asuncion and Newman, 2007). Our bounds using directional smoothness are tighter than those based on global L-smoothness of f and adapt to the optimization path. For example, on mammographic our theoretical rate for the Polyak step-size concentrates rapidly exactly when the optimizer shows fast convergence.
In-depth insights#
Directional Smoothness#
The concept of “Directional Smoothness” offers a refined analysis of gradient-based optimization methods. Traditional L-smoothness assumptions, focusing on global Lipschitz continuity of the gradient, can be overly pessimistic. Directional Smoothness relaxes this global constraint, considering the gradient’s variation along specific directions—namely, the optimization path. This localized perspective leads to tighter convergence bounds, adapting to the problem’s intrinsic geometry rather than relying on worst-case scenarios. The authors introduce various directional smoothness functions, each offering a trade-off between computational cost and bound tightness. This framework provides a more nuanced understanding of gradient descent’s behavior, explaining its success even when global smoothness assumptions are violated. The tighter bounds directly translate to improved convergence rate estimates, paving the way for better algorithm design and performance prediction.
Adaptive Step-sizes#
The concept of adaptive step-sizes is crucial for optimizing the efficiency of gradient descent methods. The core idea is to adjust the step-size at each iteration based on the local geometry of the optimization landscape, rather than relying on a fixed, globally-determined step-size. This adaptive approach is particularly advantageous when dealing with functions that lack global smoothness properties, as it allows the algorithm to navigate regions of varying curvature more effectively. The paper explores different strategies for determining these adaptive step-sizes, demonstrating how utilizing directional smoothness metrics can lead to significantly tighter convergence guarantees. The challenge lies in efficiently computing the ideal step-size at each iteration, particularly for non-quadratic functions; hence, the exploration of practical methods such as exponential search and the Polyak step-size rule is very important. Ultimately, these adaptive strategies provide a path-dependent perspective on the optimization process, capturing the unique characteristics of the function’s trajectory and potentially leading to faster convergence rates compared to traditional approaches.
Polyak’s Rate#
The Polyak step-size, a prominent adaptive learning rate method, is analyzed in the context of directional smoothness. The paper demonstrates that Polyak’s step-size achieves fast, path-dependent convergence rates without explicit knowledge of the directional smoothness function. This is a significant finding, suggesting the Polyak method’s effectiveness stems from an implicit adaptation to the local geometry of the optimization path. The analysis highlights that Polyak’s method outperforms constant step-size gradient descent, providing theoretical justification for its empirical success in various settings. The improved convergence rates are not based on global smoothness assumptions, offering more practical applicability to non-uniformly smooth functions. Furthermore, the theoretical guarantees derived for Polyak’s step-size are shown to be tighter than classical convergence analyses based on L-smoothness assumptions, demonstrating a crucial advantage of considering path-dependent properties.
Convergence Bounds#
The research paper delves into novel convergence bounds for gradient descent methods, moving beyond traditional L-smoothness assumptions. Directional smoothness, a key concept, measures gradient variation along the optimization path rather than relying on global worst-case constants. This allows for tighter, path-dependent bounds that adapt to the problem’s local geometry. The analysis reveals that step-size adaptation significantly improves convergence rates, though computing ideal step sizes can be computationally intensive. The study also shows that classical methods, such as the Polyak step-size and normalized gradient descent, achieve fast convergence rates without requiring explicit knowledge of directional smoothness. Experiments on logistic regression confirm that the new convergence bounds are significantly tighter than those derived from global smoothness, offering valuable insights for practical optimization.
Future Research#
Future research directions stemming from this work on directional smoothness could explore extensions to non-convex optimization problems. While the paper establishes strong results for convex functions, investigating the behavior and convergence guarantees in non-convex settings is crucial for broader applicability, especially in deep learning. Further research should focus on developing more efficient algorithms for computing strongly adapted step-sizes. The current methods, while effective, can be computationally intensive. Exploring alternative methods, potentially leveraging approximation techniques or exploiting problem structure, would significantly enhance practicality. Finally, a key area for future work involves a deeper investigation into the relationship between directional smoothness and existing smoothness concepts, such as L-smoothness and Hölder continuity. This could lead to a more unified theoretical framework for analyzing gradient descent methods and potentially reveal new insights into the optimization landscape of various functions.
More visual insights#
More on figures
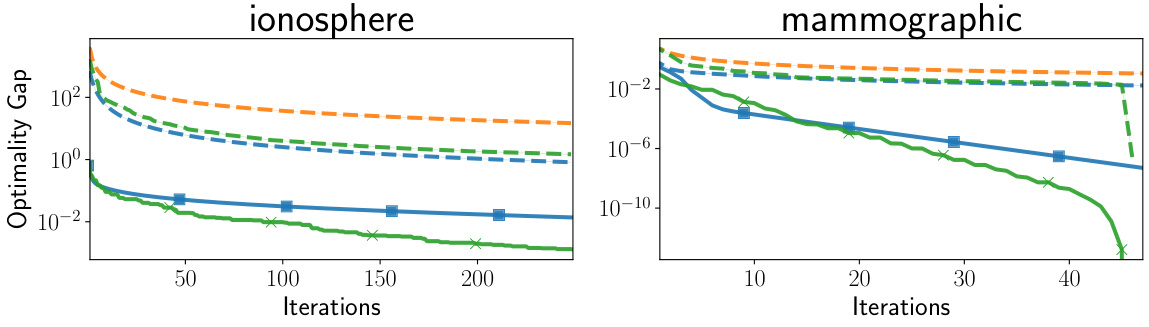
🔼 The figure illustrates how the directional smoothness (Mk) provides a tighter upper bound on the function’s behavior compared to the global L-smoothness. It shows that even though a step-size of 1/L minimizes the upper bound based on global smoothness, the actual progress of gradient descent is better approximated by the directional smoothness (Mk) which is often much smaller than L. This tighter bound leads to improved convergence rate guarantees.
read the caption
Figure 2: Illustration of GD with ηκ = 1/L. Even though this step-size exactly minimizes the upper-bound from L-smoothness, Mk directional smoothness better predicts the progress of the gradient step because Mk ≪ L. Our rates improve on L-smoothness because of this tighter bound.
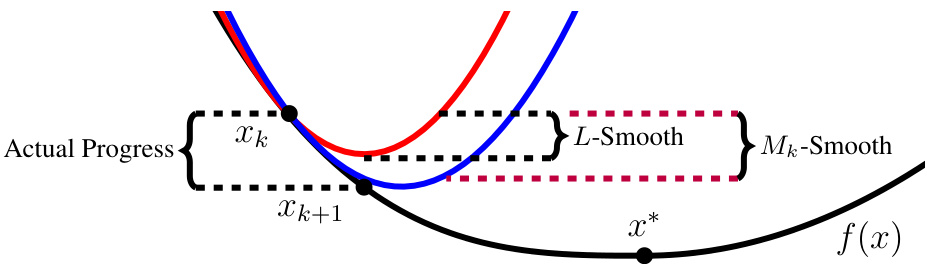
🔼 This figure compares the performance of Gradient Descent (GD) with different step size rules on a synthetic quadratic problem. Three different step size strategies are compared: 1/L (constant step size based on global L-smoothness), 1/Dk (step size adapted to point-wise directional smoothness), and 1/Ak (step size adapted to path-wise directional smoothness). The figure shows three plots: optimality gap, point-wise smoothness, and adapted step sizes over 20,000 iterations. It highlights how adaptive step sizes based on directional smoothness lead to faster convergence than constant step size.
read the caption
Figure 3: Performance of GD with different step-size rules for a synthetic quadratic problem. We run GD for 20,000 steps on 20 random quadratic problems with L = 1000 and Hessian skew. Left-to-right, the first plot shows the optimality gap f(xk) − f(x*), the second shows the point-wise directional smoothness D(xk, Xk+1), and the third shows step-sizes used by the different methods.

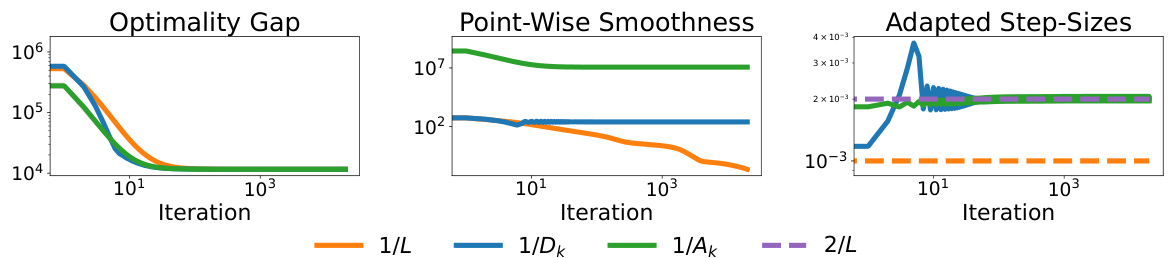
🔼 This figure compares the performance of several gradient descent methods on three logistic regression datasets: ionosphere, horse-colic, and ozone. The methods compared are Gradient Descent (GD) with a constant step size (1/L), GD with step sizes adapted to the pointwise directional smoothness (1/Dk), Polyak step size, Normalized Gradient Descent, and an adaptive gradient descent method (AdGD). The results show that the adaptive step size methods generally outperform the constant step size method, particularly on the horse-colic dataset, which exhibits linear convergence for the adaptive methods.
read the caption
Figure 4: Comparison of GD with ηκ = 1/L, step-sizes strongly adapted to the point-wise smoothness (ηκ = 1/D(xk, Xk+1)), and the Polyak step-size against normalized GD (Norm. GD) and the AdGD method on three logistic regression problems. AdGD uses a smoothed version of the point-wise directional smoothness from the previous iteration to set ηκ. We find that GD methods with adaptive step-sizes consistently outperform GD with ηκ = 1/L and even obtain a linear rate on horse-colic.
Full paper#