TL;DR#
Large Language Models (LLMs) often suffer from overconfidence, especially when fine-tuned with limited data. Existing methods to address this issue, such as post-training Bayesianization, have limitations. These methods struggle to accurately estimate uncertainty in different scenarios, including during the fine-tuning process itself.
This paper introduces Bayesian Low-Rank Adaptation by Backpropagation (BLOB), a novel approach for addressing overconfidence in LLMs. BLOB continuously and jointly adjusts both the mean and covariance of LLM parameters throughout fine-tuning. This allows for more accurate uncertainty estimation and better generalization performance on both in-distribution and out-of-distribution data. The study provides empirical evidence and publicly available code to support its findings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reliable and responsible large language models (LLMs). It addresses the critical issue of overconfidence in LLMs, particularly when fine-tuned on limited data, offering a novel approach that significantly improves generalization and uncertainty estimation. The proposed method, BLOB, provides a new avenue for research into Bayesian deep learning techniques for LLMs, and can improve the deployment of LLMs for various applications. The empirical results are compelling and the code is publicly available, making it easily reproducible and readily adaptable for various downstream tasks.
Visual Insights#
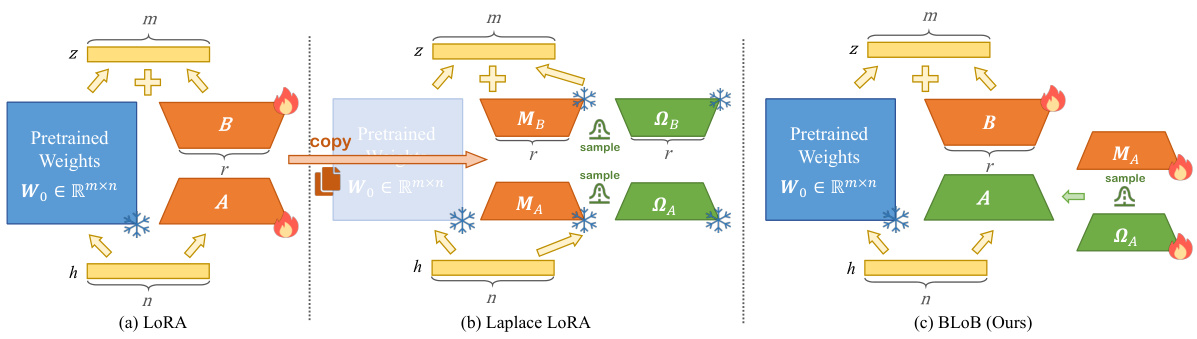
🔼 This figure compares three different methods for Bayesianizing Low-Rank Adaptation (LoRA) for Large Language Models (LLMs). (a) shows the standard LoRA approach, which only updates low-rank matrices B and A. (b) shows the Laplace LoRA method which approximates the posterior distribution of the parameters. Finally, (c) presents the proposed BLoB method, which jointly learns the mean and covariance of the low-rank matrices using backpropagation during the entire fine-tuning process.
read the caption
Figure 1: Overview of our Bayesian Low-Rank Adaptation by Backpropagation, i.e., BLoB (right) as well as comparison with existing methods such as LoRA (left) and Laplace LoRA (middle).
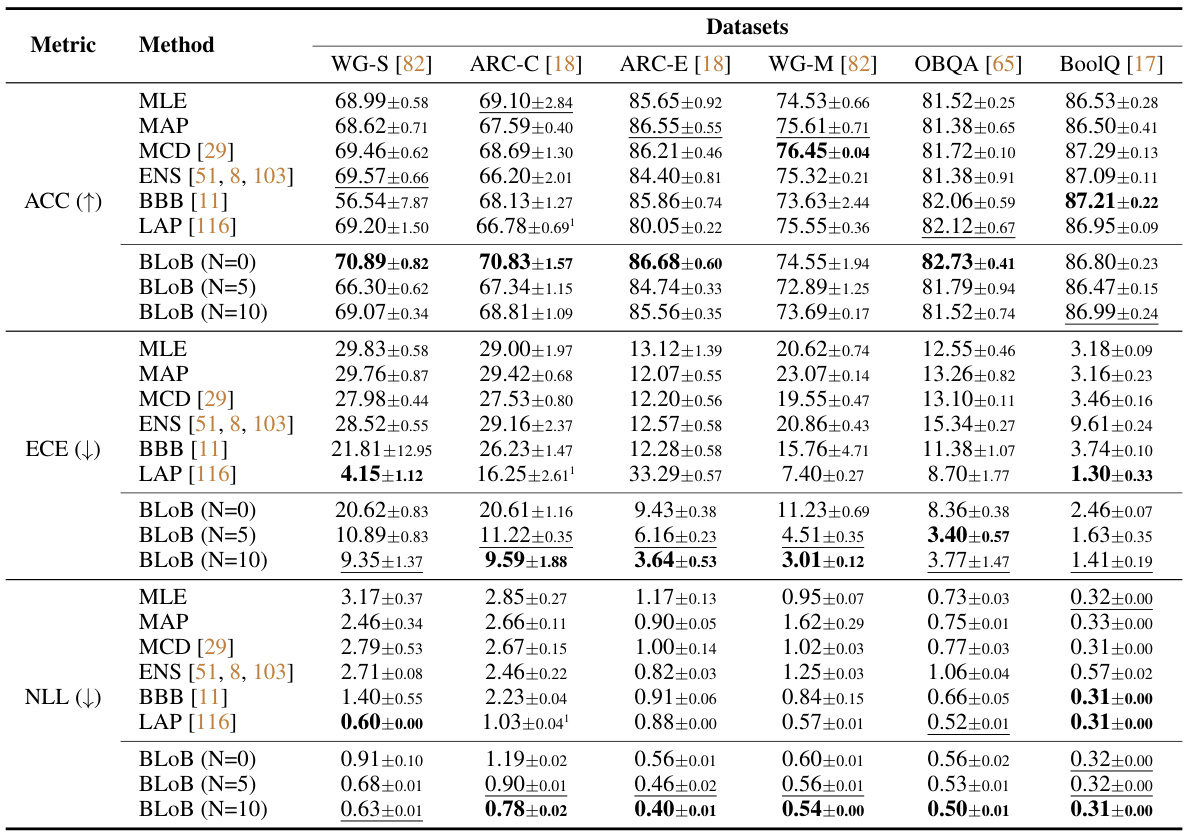
🔼 This table presents the performance comparison of different uncertainty estimation methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB) applied to the LoRA on Llama2-7B pre-trained weights. The evaluation metrics include accuracy (ACC), expected calibration error (ECE), and negative log-likelihood (NLL) across six common-sense reasoning datasets. The number of samples (N) used during inference for BLOB is also varied (N=0, 5, 10). The results show BLOB’s superior performance in terms of accuracy and uncertainty estimation.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.
In-depth insights#
BLOB: Bayesian LLM Tuning#
BLOB: Bayesian LLM Tuning presents a novel approach to fine-tuning large language models (LLMs) by integrating Bayesian principles directly into the training process. This contrasts with post-training Bayesian methods, which often suffer from limitations due to the pre-trained parameters. BLOB’s key innovation is the continuous and joint adjustment of both the mean and covariance of LLM parameters throughout fine-tuning. This allows for a more accurate estimation of uncertainty and improved model calibration. The method leverages low-rank adaptation (LoRA) to maintain computational efficiency, which is crucial for working with large LLMs. Empirical results suggest that BLOB achieves better generalization and uncertainty quantification compared to existing methods, particularly on out-of-distribution data. The low-rank structure of BLOB’s variational distributions helps ensure computational tractability and efficient backpropagation. However, limitations exist including the reliance on sampling during inference and current focus on classification tasks. Further investigation is needed to explore the impact on text generation tasks.
Low-Rank Adaptation#
Low-rank adaptation techniques, such as LoRA, are crucial for efficiently fine-tuning large language models (LLMs). They reduce computational costs by updating only a small subset of the model’s parameters, improving model performance without retraining the entire network. The low-rank assumption implies that the model’s weight matrices have a low intrinsic dimensionality. This allows for significant parameter reduction, making it feasible to fine-tune LLMs on resource-constrained hardware or when dealing with limited data. However, the choice of low-rank approximation and its impact on model accuracy and generalization is critical. This involves a trade-off between the computational efficiency gained by using a lower-rank approximation, and the potential loss of performance due to information loss. Bayesian methods offer a way to quantify the uncertainty associated with these approximations thereby improving reliability and providing a more principled approach to handling limited data or domain-specific tasks. Further research into optimal low-rank structures and the development of effective Bayesian low-rank methods will likely improve LLM efficiency and reliability.
Variational Inference#
Variational inference is a powerful approximate inference technique for complex probability distributions, especially those encountered in Bayesian machine learning models. It avoids the intractability of exact Bayesian inference by introducing a simpler, tractable distribution (the variational distribution) to approximate the true posterior. The goal is to find the variational distribution that is closest to the true posterior, typically measured by the Kullback-Leibler (KL) divergence. This optimization process is often performed using gradient-based methods, making it computationally feasible even for high-dimensional models. A key advantage of variational inference is its scalability, allowing for the analysis of models that are otherwise intractable. Different variational families can be used, such as Gaussian or mean-field approximations, each offering a different trade-off between accuracy and computational cost. However, the choice of variational family and the method of optimization significantly impact the accuracy of the approximation, and careful consideration is needed to ensure reliability. Careful selection of the variational family and a well-designed optimization strategy are crucial to obtaining good results. Despite its approximations, variational inference provides a practical and efficient tool for handling Bayesian models, enabling insights that would be otherwise unobtainable.
Uncertainty Estimation#
The research paper explores uncertainty estimation in large language models (LLMs), focusing on the challenges posed by their overconfidence, especially when fine-tuned on limited data for downstream tasks. Bayesian methods are presented as a natural way to address this issue by modeling the uncertainty inherent in the parameters of the LLM, improving calibration and reliability. The paper proposes a novel method, Bayesian Low-Rank Adaptation by Backpropagation (BLoB), which differs from previous approaches by jointly tuning both the mean and covariance of the parameters, which are often approximated during inference. The methodology incorporates low-rank adaptation (LoRA) to enhance efficiency, thus offering a more principled approach than post-training Bayesian methods. Experimental results demonstrate BLoB’s improved performance in generalization and uncertainty quantification on both in-distribution and out-of-distribution datasets, highlighting the method’s ability to mitigate overconfidence and enhance model robustness.
OOD Generalization#
Out-of-distribution (OOD) generalization is a crucial aspect of evaluating the robustness and reliability of machine learning models, especially large language models (LLMs). Effective OOD generalization means a model’s ability to perform well on data that differs significantly from its training distribution. This is vital for real-world applications where LLMs encounter unforeseen inputs or situations. Research in this area focuses on developing techniques to improve a model’s ability to handle such unexpected data. This might involve designing models with inherent uncertainty quantification mechanisms, leveraging data augmentation strategies to expand the training data’s diversity, or employing techniques like meta-learning or domain adaptation to better generalize across different domains. A key challenge is that OOD data is inherently difficult to define and assess. There’s no single universally accepted benchmark for evaluating OOD generalization. Thus, the effectiveness of OOD techniques is often evaluated on multiple diverse datasets, measuring performance across varied distribution shifts and uncertainty estimates. Future research directions in OOD generalization include further exploring the interplay between model architecture, training methods, and uncertainty quantification, as well as developing standardized benchmarks for assessing this crucial model capability.
More visual insights#
More on figures
🔼 This figure compares three different methods for Bayesianizing Low-Rank Adaptation (LoRA) in large language models. The left panel shows the standard LoRA approach. The middle panel shows the Laplace LoRA method. The right panel shows the authors’ proposed Bayesian Low-Rank Adaptation by Backpropagation (BLoB) method. BLoB differs from the others by jointly adjusting the mean and covariance of LLM parameters during fine-tuning, instead of performing approximate Bayesian estimation post-training. The figure highlights the differences in how each method handles the weight updates and incorporates Bayesian inference.
read the caption
Figure 1: Overview of our Bayesian Low-Rank Adaptation by Backpropagation, i.e., BLoB (right) as well as comparison with existing methods such as LoRA (left) and Laplace LoRA (middle).

🔼 This figure compares three different methods for Bayesianizing Low-Rank Adaptation (LoRA) for Large Language Models (LLMs): standard LoRA, Laplace LoRA, and the proposed method, Bayesian Low-Rank Adaptation by Backpropagation (BLoB). It visually illustrates the key differences in how each method handles the weight update matrices (A and B) within the LoRA framework during fine-tuning, specifically showing how BLoB jointly estimates both mean and covariance, unlike the others. This simultaneous estimation allows for more accurate uncertainty quantification.
read the caption
Figure 1: Overview of our Bayesian Low-Rank Adaptation by Backpropagation, i.e., BLoB (right) as well as comparison with existing methods such as LoRA (left) and Laplace LoRA (middle).
🔼 This figure compares three different methods for Bayesian Low-Rank Adaptation: LoRA, Laplace LoRA, and the proposed BLoB method. LoRA is shown on the left, and it only updates the weights with a rank-r matrix, which is efficient but doesn’t account for uncertainty. Laplace LoRA (middle) adds uncertainty by approximating the posterior distribution after training. BLoB (right), the proposed method, jointly updates the mean and covariance of the low-rank matrices during training, which allows for continuous and joint adjustment of both mean and covariance, thus providing better uncertainty estimation and generalization.
read the caption
Figure 1: Overview of our Bayesian Low-Rank Adaptation by Backpropagation, i.e., BLoB (right) as well as comparison with existing methods such as LoRA (left) and Laplace LoRA (middle).

🔼 This figure compares three different methods for Bayesianizing LoRA: standard LoRA, Laplace LoRA, and the proposed BLoB method. Standard LoRA only updates the weights with a single point estimate. Laplace LoRA approximates the Bayesian posterior with a Laplace approximation. The proposed BLoB method jointly updates the mean and variance of the parameters throughout the fine-tuning process.
read the caption
Figure 1: Overview of our Bayesian Low-Rank Adaptation by Backpropagation, i.e., BLoB (right) as well as comparison with existing methods such as LoRA (left) and Laplace LoRA (middle).
More on tables
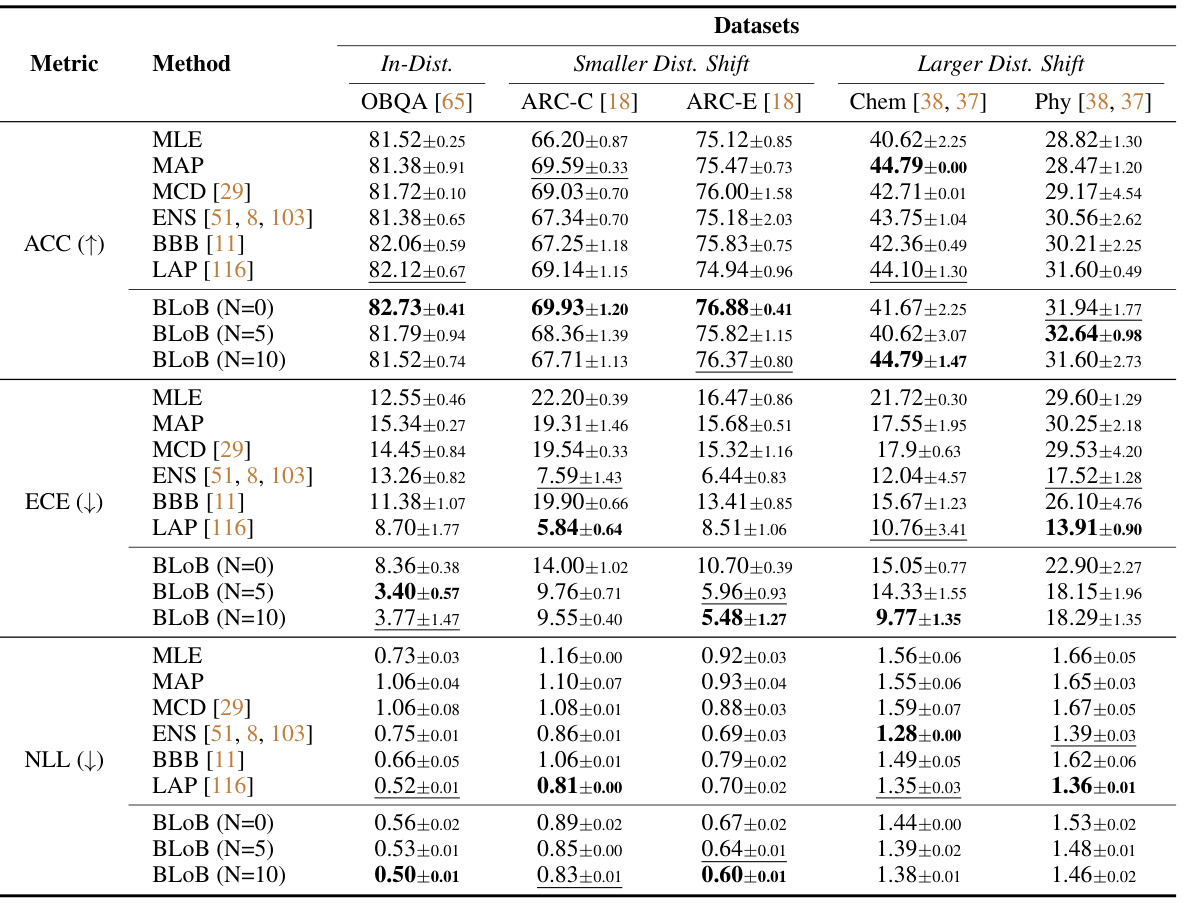
🔼 This table presents the performance comparison of different uncertainty estimation methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB) applied to LoRA on Llama2-7B pre-trained weights across six common-sense reasoning datasets. The metrics used for comparison are accuracy (ACC), expected calibration error (ECE), and negative log-likelihood (NLL). The table highlights the impact of the number of samples (N) during inference for the BLOB method.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.
🔼 This table compares the performance of various Bayesian methods (BLOB, BBB, MCD, ENS, LAP) against standard Maximum Likelihood Estimation (MLE) and Maximum A Posteriori (MAP) methods. The comparison is done across six different common sense reasoning tasks using the same hyperparameters and after 5000 gradient steps. The metrics used for evaluation are Accuracy (ACC), Expected Calibration Error (ECE), and Negative Log-Likelihood (NLL). The number of samples used during inference (N) for BLOB is varied to show the impact of sampling on performance. Bold values indicate the best performing method for each metric, and underlined values indicate the second-best.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.

🔼 This table compares the performance of different methods for applying Bayesian Low-Rank Adaptation (LoRA) to a Llama2-7B pre-trained language model across six common sense reasoning tasks. It shows accuracy (ACC), expected calibration error (ECE), and negative log-likelihood (NLL) for various methods, including Maximum Likelihood Estimation (MLE), Maximum A Posteriori (MAP), Monte Carlo Dropout (MCD), Deep Ensemble (ENS), Bayes by Backprop (BBB), Laplace LoRA (LAP), and the proposed BLOB method with varying numbers of samples (N) during inference. Higher ACC and lower ECE/NLL values indicate better performance.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.

🔼 This table compares the performance of various uncertainty estimation methods applied to the LoRA adapter on Llama2-7B pre-trained weights across six common-sense reasoning datasets. Metrics include Accuracy (ACC), Expected Calibration Error (ECE), and Negative Log-Likelihood (NLL). The number of inference samples (N) for BLOB is varied to show its impact. Higher ACC is better; lower ECE and NLL are better.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.

🔼 This table compares the performance of different methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB with different sample sizes N) on six common-sense reasoning tasks using Llama2-7B pre-trained weights. The metrics used are Accuracy (ACC), Expected Calibration Error (ECE), and Negative Log-Likelihood (NLL). It shows how well each method calibrates its confidence and its overall accuracy and uncertainty estimation.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.

🔼 This table presents the performance comparison of several methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB with different sample numbers) for fine-tuning LLMs on six common-sense reasoning tasks using LoRA. The metrics used for evaluation include Accuracy (ACC), Expected Calibration Error (ECE), and Negative Log-Likelihood (NLL), reflecting both performance and uncertainty estimation. The table highlights the superior performance of the proposed BLOB method, particularly when considering uncertainty estimation.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.
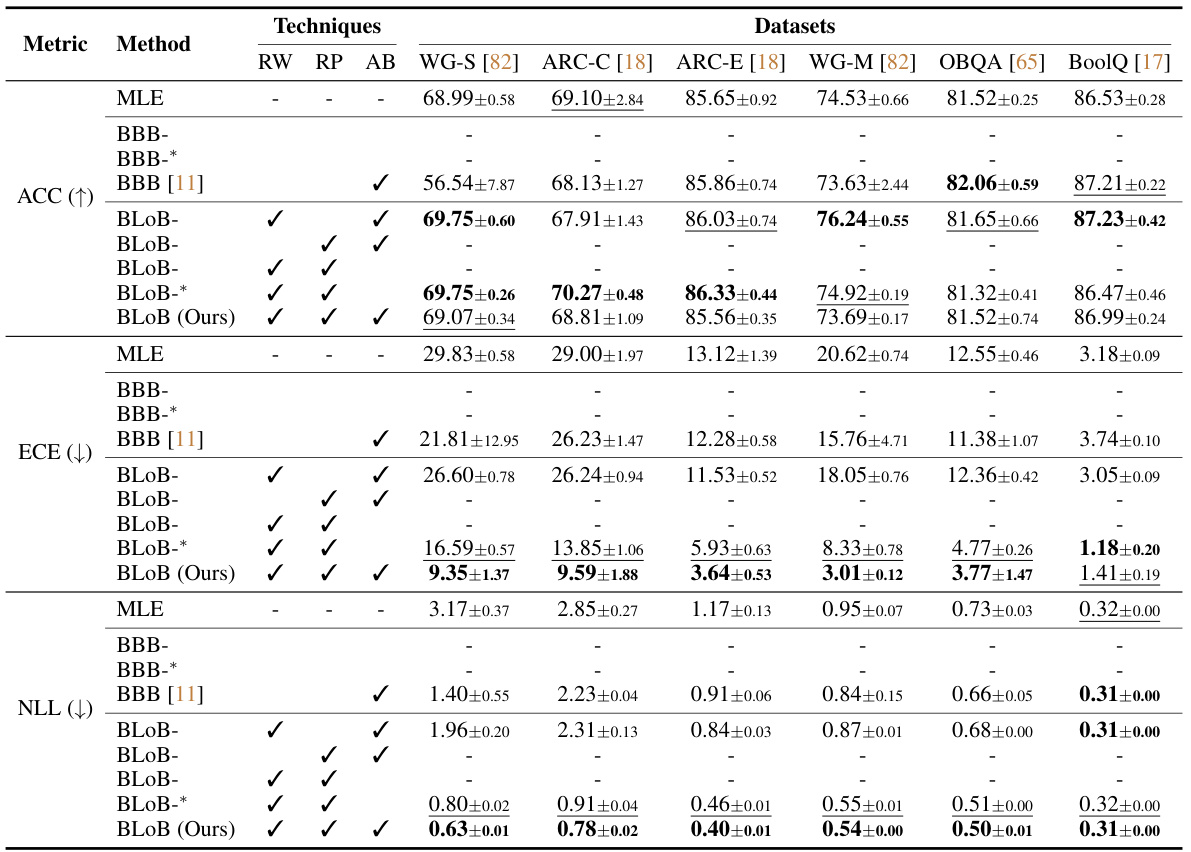
🔼 This table compares the performance of various Bayesian methods (including the proposed BLOB) and maximum likelihood/maximum a posteriori estimation baselines on six common sense reasoning datasets. Performance is measured by accuracy, expected calibration error, and negative log-likelihood, reflecting both predictive accuracy and uncertainty calibration. The impact of varying the number of samples used during inference with BLOB is also explored.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.

🔼 This table compares the performance of various methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB) for adapting a Llama2-7B language model using LoRA to six common-sense reasoning tasks. The metrics used are accuracy (ACC) and expected calibration error (ECE), both shown as percentages. The table highlights the impact of the number of samples (N) used during inference for the BLOB method.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. “↑” and “↓” indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.
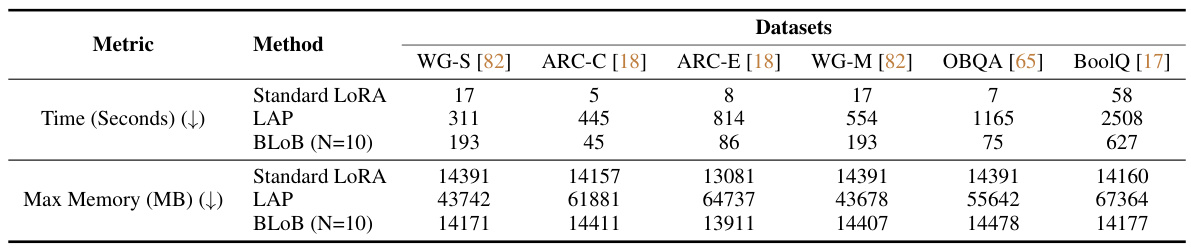
🔼 This table compares the performance of several methods (MLE, MAP, MCD, ENS, BBB, LAP, and BLOB) for adapting Llama2-7B language models using LoRA on six common sense reasoning tasks. The metrics used are accuracy (ACC), expected calibration error (ECE), and negative log-likelihood (NLL). Different numbers of samples (N) during inference are tested for BLOB to show the impact on performance. The best and second-best performances are highlighted.
read the caption
Table 1: Performance of different methods applied to LoRA on Llama2-7B pre-trained weights, where Accuracy (ACC) and Expected Calibration Error (ECE) are reported in percentages. The evaluation is done across six common-sense reasoning tasks with a shared hyper-parameter setting after 5,000 gradient steps. We use N to represent the number of samples during inference in BLOB. '↑' and '↓' indicate that higher and lower values are preferred, respectively. Boldface and underlining denote the best and the second-best performance, respectively.
Full paper#



















