TL;DR#
Online composite optimization, where learners iteratively make decisions and suffer losses, has traditionally focused on either purely stochastic or adversarial environments. This research paper addresses a critical gap by introducing the Stochastically Extended Adversarial (SEA) model, which considers intermediate scenarios between these two extremes. The paper highlights challenges in adapting existing algorithms to this new setting due to the presence of non-smooth regularizers that are common in practice. Existing algorithms are often designed to work on smooth loss functions and thus do not efficiently work in scenarios that include non-smooth regularizers.
To address these issues, the paper proposes the Optimistic Composite Mirror Descent (OptCMD) algorithm for online composite optimization within the SEA framework. OptCMD is designed to efficiently handle both stochastic and adversarial aspects of the environment, while also leveraging the advantages provided by the regularizer in composite losses. The algorithm achieves optimal regret bounds (a measure of performance) for three types of time-varying functions: general convex, strongly convex, and exp-concave. Further, to address situations where the exact function type is unknown, the paper introduces a novel multi-level universal algorithm. This algorithm adapts dynamically to the characteristics of the environment and achieves similar optimal bounds. The research shows that using regularizers does not increase the regret bound, confirming the beneficial nature of regularizers.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between purely stochastic and adversarial online composite optimization. It introduces the composite SEA model, offering a more realistic setting for real-world applications. The proposed OptCMD algorithm and universal strategy provide robust and efficient solutions for various function types, opening avenues for further research in handling uncertainty and composite losses.
Visual Insights#

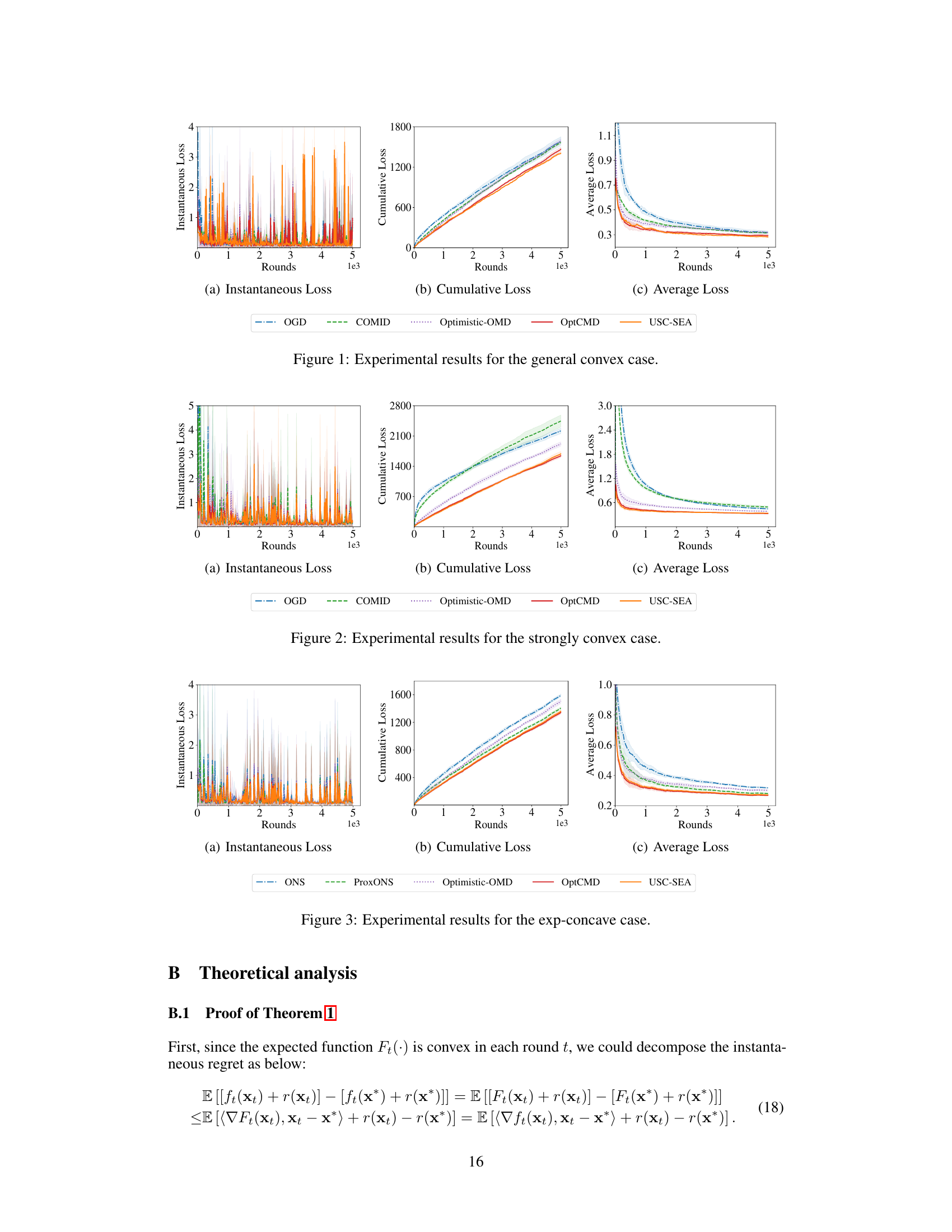
🔼 This figure presents the experimental results for the general convex case. It shows three subplots displaying the instantaneous loss, cumulative loss, and average loss across multiple algorithms (OGD, COMID, Optimistic-OMD, OptCMD, and USC-SEA) over 5000 rounds. The instantaneous loss plot illustrates the loss at each round, highlighting the fluctuations. The cumulative loss shows the accumulated loss over time, illustrating the performance of each algorithm. Finally, the average loss indicates the average loss per round, providing a metric for overall performance comparison.
read the caption
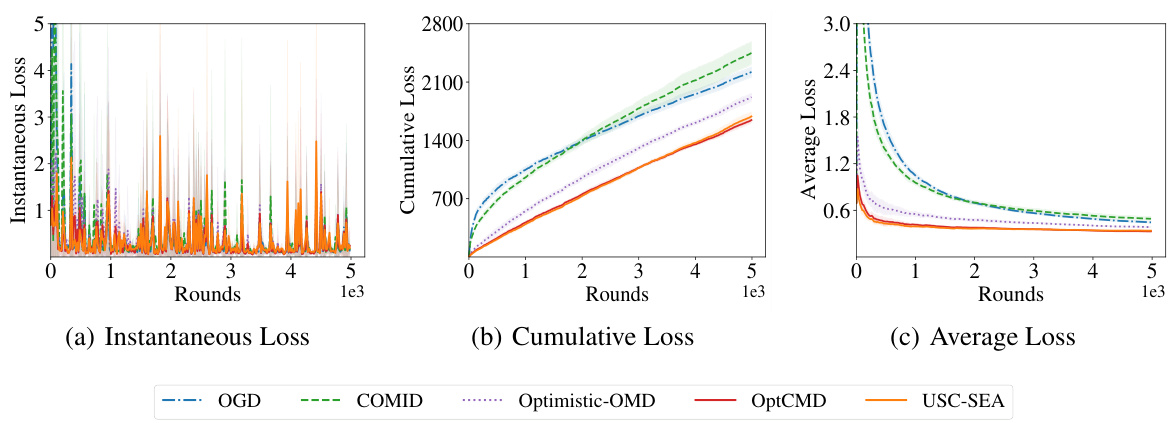
Figure 1: Experimental results for the general convex case.

🔼 This table presents the pseudocode for the Optimistic Composite Mirror Descent algorithm (OptCMD). The algorithm is iterative, taking place over T rounds. In each round, the learner submits a decision xt, receives a composite loss function ft(xt)+r(xt) where ft is sampled from a distribution Dt provided by the environment, and updates its decision for the next round using the Bregman divergence. This table is central to understanding how the algorithm functions and adapts in the stochastically extended adversarial environments discussed in the paper.
read the caption
Algorithm 1 Optimistic Composite Mirror Descent (OptCMD)
In-depth insights#
Composite SEA Model#
The hypothetical “Composite SEA Model” extends the Stochastically Extended Adversarial (SEA) model to encompass online composite optimization problems. This is crucial because real-world scenarios rarely present purely stochastic or adversarial data; instead, they often exhibit a mixture of both. The composite aspect incorporates a fixed, non-smooth regularizer into the loss function, making the model more applicable to problems involving sparsity or other structural constraints. By analyzing regret bounds under this hybrid model, researchers can gain insights into algorithm performance in diverse and unpredictable environments. The framework could bridge the gap between purely stochastic and adversarial online learning settings, thereby enabling development of more robust and efficient algorithms for practical applications. A key challenge would be developing effective algorithms that adapt to the unknown mix of stochasticity and adversariality present in the data.
OptCMD Algorithm#
The OptCMD (Optimistic Composite Mirror Descent) algorithm is a key contribution of this research paper, designed to tackle online composite optimization problems within stochastically extended adversarial (SEA) environments. OptCMD cleverly separates the handling of the smooth and non-smooth components of the loss function, which is crucial because existing methods for SEA struggle with non-smooth regularizers. The algorithm’s optimistic nature leverages predictions of future gradients to improve decision-making, especially valuable in the unpredictable SEA setting. The paper analyzes OptCMD’s performance under different convexity assumptions (general convex, strongly convex, and exp-concave), providing regret bounds that are competitive with existing algorithms for stochastic or adversarial settings alone, demonstrating that OptCMD effectively handles the complexities of both stochastic and adversarial influences simultaneously. Furthermore, the paper addresses the practical limitation of needing to know the function type beforehand by proposing a universal algorithm that adapts to different loss function types dynamically. This demonstrates the versatility and robustness of the core OptCMD approach.
Universal Strategy#
The heading ‘Universal Strategy’ likely refers to a method designed to handle various scenarios within online composite optimization without requiring prior knowledge of the specific type of loss function. This is crucial because real-world problems rarely conform neatly to purely stochastic or adversarial settings. A universal strategy aims to achieve strong performance guarantees across diverse scenarios, adapting its behavior to whichever setting is actually encountered. The core idea is likely to employ a meta-algorithm that learns from, and combines, the outcomes of multiple specialized algorithms or “experts”, each designed for a particular type of loss function (e.g., stochastic, adversarial, or intermediate). The meta-algorithm dynamically weighs these experts based on their past performance, effectively creating a robust and adaptable system that can handle unseen data distributions with minimal loss in optimality. This approach is highly valuable because it greatly reduces the risk of poor performance when facing unforeseen circumstances and increases the reliability and generalizability of the optimization process.
Regret Bounds#
The research paper analyzes regret bounds in online composite optimization, a setting where a learner iteratively makes decisions and incurs losses in either stochastic or adversarial environments or a combination of both. Key findings revolve around the optimistic composite mirror descent (OptCMD) algorithm, showing its effectiveness in achieving various regret bounds depending on the characteristics of the loss functions (general convex, strongly convex, exp-concave). The analysis highlights the impact of the cumulative stochastic variance and adversarial variation on regret, offering regret bounds that gracefully adapt to the degree of stochasticity and adversarism in the environment. Importantly, the results demonstrate that the inclusion of a fixed regularizer does not worsen the regret bounds, providing a strong argument for its practical use. Finally, a universal algorithm is proposed to address the issue of unknown function type, capable of achieving similar regret bounds without needing prior knowledge of the problem structure.
Future Works#
The paper’s conclusion, implicitly suggesting avenues for future research, could significantly benefit from an explicitly titled ‘Future Work’ section. Extending the composite SEA model to handle non-convex loss functions is a crucial next step, considering the prevalence of non-convexity in real-world problems. Similarly, relaxing the boundedness assumptions on the domain and gradients would enhance the model’s practicality and applicability. Developing computationally efficient algorithms for the universal strategy is also needed to improve scalability. Finally, empirical evaluation on a wider range of datasets and with more comprehensive comparisons against existing methods is essential to validate the theoretical claims and showcase the practical advantages of the proposed approach. Addressing these points would further strengthen the paper and increase its impact on the field of online composite optimization.
More visual insights#
More on figures
🔼 This figure presents the experimental results for the general convex case, comparing several online optimization algorithms. The left panel shows the instantaneous loss per round; the middle panel illustrates the cumulative loss over time, which represents the total loss accumulated during the learning process; and the right panel displays the average loss per round, showing the average loss incurred in each round of optimization. These three aspects help to analyze and compare the performance of different algorithms in handling general convex loss functions within the context of the Stochastically Extended Adversarial (SEA) model. The algorithms compared include OGD, COMID, Optimistic-OMD, OptCMD (the proposed algorithm), and USC-SEA (a universal strategy for composite SEA).
read the caption
Figure 1: Experimental results for the general convex case.
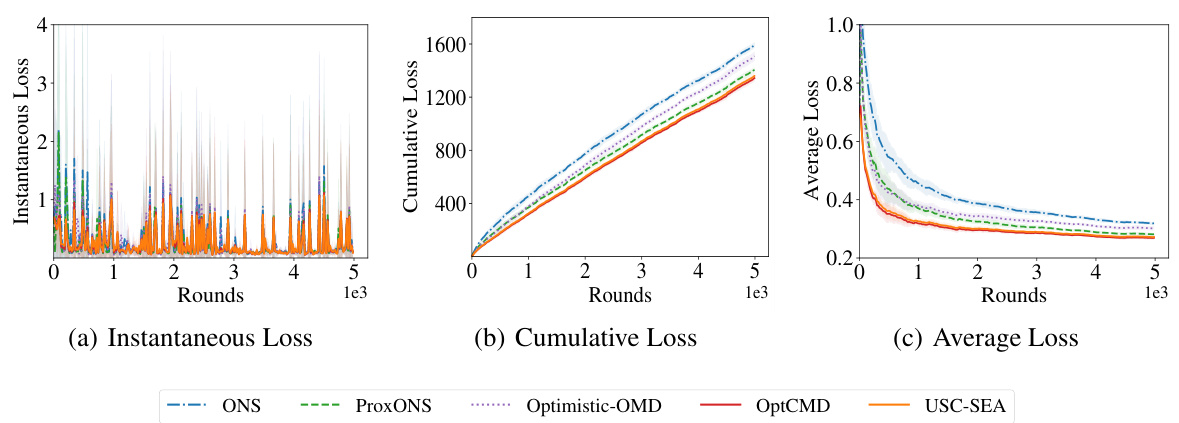
🔼 This figure shows the experimental results for the exp-concave case. It includes three subfigures showing the instantaneous loss, cumulative loss, and average loss for different algorithms (ONS, ProxONS, Optimistic-OMD, OptCMD, and USC-SEA) over 5000 rounds. The results demonstrate that OptCMD and USC-SEA achieve lower losses compared to baseline methods, indicating their better performance in handling the composite SEA environment.
read the caption
Figure 3: Experimental results for the exp-concave case.
Full paper#