TL;DR#
Stochastic spiking neural networks (SSNNs) are powerful models for neuronal dynamics but notoriously difficult to train due to event discontinuities and noise. Existing methods often rely on surrogate gradients or an optimise-then-discretise approach, which yield less accurate or only approximate gradients. These limitations hinder the development of truly bio-plausible and efficient learning algorithms for SSNNs.
This research introduces a mathematically rigorous framework, based on rough path theory, to model SSNNs as stochastic differential equations with event discontinuities. This framework allows for noise in both spike timing and network dynamics. By identifying sufficient conditions for the existence of pathwise gradients, the authors derive a recursive relation for exact gradients. They further introduce a new class of signature kernels for training SSNNs as generative models and provide an end-to-end autodifferentiable solver.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel, mathematically rigorous framework for training stochastic spiking neural networks (SSNNs), a significant challenge in the field. This opens new avenues for developing more biologically plausible and efficient learning algorithms for SSNNs, advancing both theoretical understanding and practical applications in neuroscience and AI.
Visual Insights#
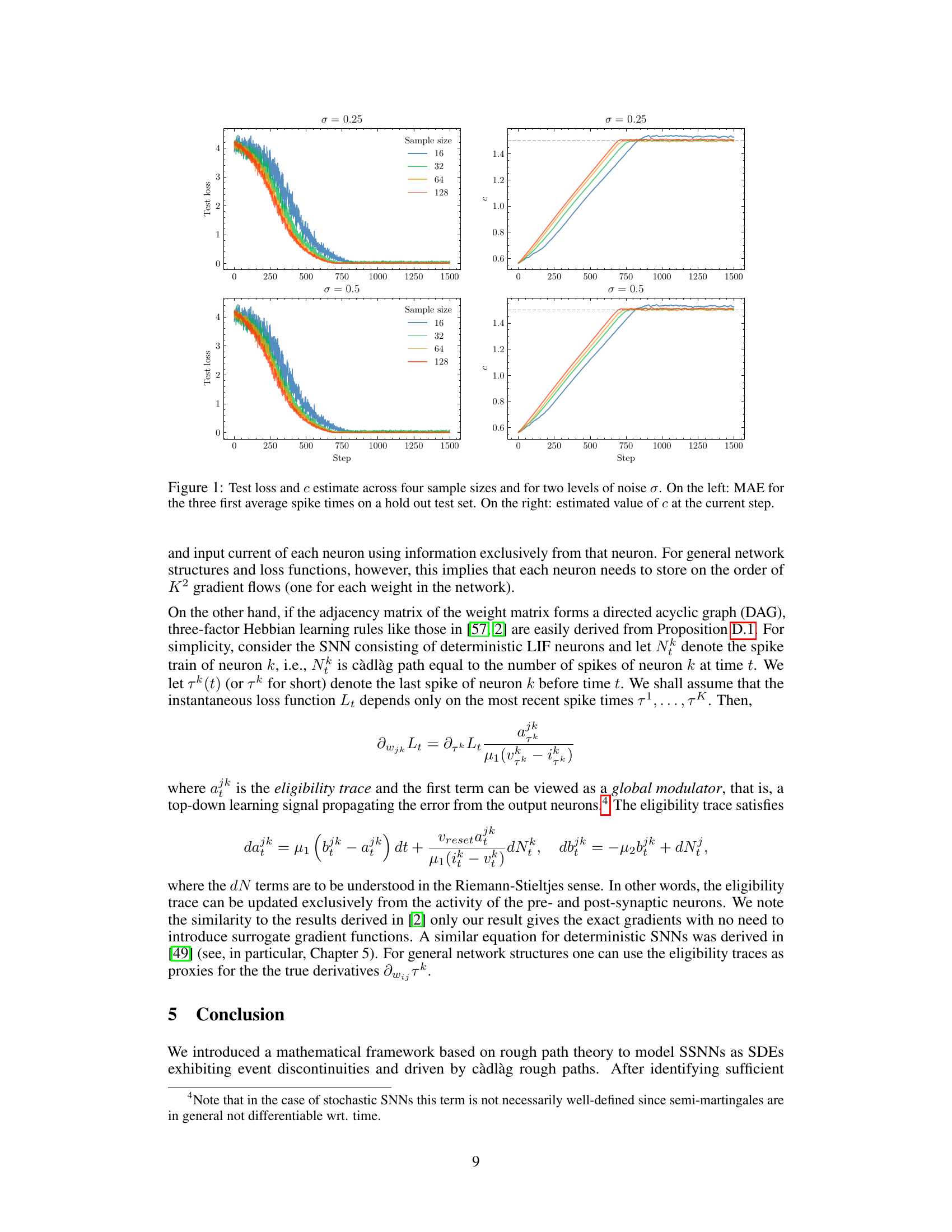
🔼 This figure shows the results of an experiment to estimate the input current (c) of a single stochastic leaky integrate-and-fire (SLIF) neuron. The left panel displays the mean absolute error (MAE) for the first three average spike times on a hold-out test set, and the right panel shows the estimated value of c at each step during stochastic gradient descent. Multiple lines represent different sample sizes (16, 32, 64, 128) and both panels show results for two different noise levels (σ = 0.25 and σ = 0.5).
read the caption
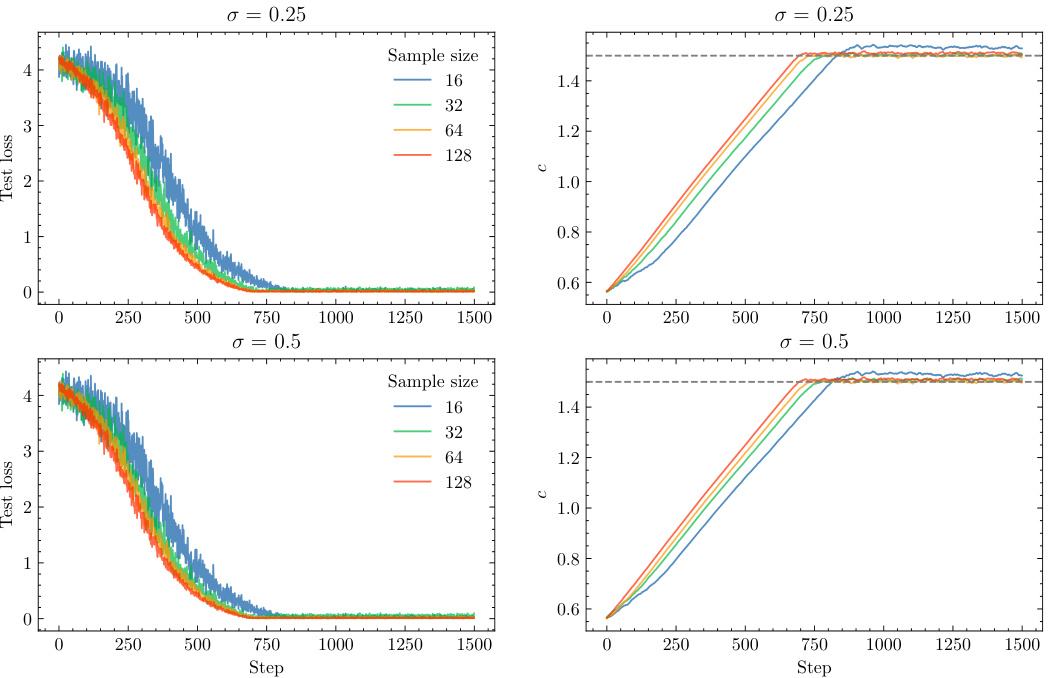
Figure 1: Test loss and c estimate across four sample sizes and for two levels of noise σ. On the left: MAE for the three first average spike times on a hold out test set. On the right: estimated value of c at the current step.

🔼 The figure shows the results of an experiment to estimate the constant input current c of a single stochastic leaky integrate-and-fire neuron model. Two levels of noise (σ = 0.25 and σ = 0.5) and four sample sizes (16, 32, 64, and 128) were tested. The left panel shows the mean absolute error (MAE) for the first three average spike times on a hold-out test set, while the right panel shows the estimated value of c at each step of the stochastic gradient descent optimization process. The results demonstrate that the model can accurately learn the input current even in the presence of noise and with relatively small sample sizes.
read the caption
Figure 1: Test loss and c estimate across four sample sizes and for two levels of noise σ. On the left: MAE for the three first average spike times on a hold out test set. On the right: estimated value of c at the current step.
Full paper#