TL;DR#
The rise of data-driven machine learning has highlighted privacy concerns. Existing differentially private (DP) kernel learning methods suffer from scalability issues, restricted kernel choices, or dependence on test data. These limitations hinder the application of powerful kernel methods to privacy-sensitive tasks, which require efficient and privacy-preserving techniques.
This research introduces DP-scalable kernel learning algorithms that overcome these limitations. The core innovation is the use of a DP K-means Nyström method, a low-rank approximation technique. This approach allows for efficient computation on large datasets with general kernels and provides theoretical guarantees for privacy and accuracy. The experiments demonstrate the superior performance of the proposed methods, confirming both theoretical claims and practical utility.
Key Takeaways#
Why does it matter?#
This paper is important because it presents scalable and privacy-preserving algorithms for general kernel learning, a significant challenge in machine learning. It addresses limitations of existing methods by utilizing the Nyström method, improving efficiency and expanding the range of applicable kernels. This work opens new avenues for research in private machine learning and enables the use of more complex models in privacy-sensitive applications.
Visual Insights#
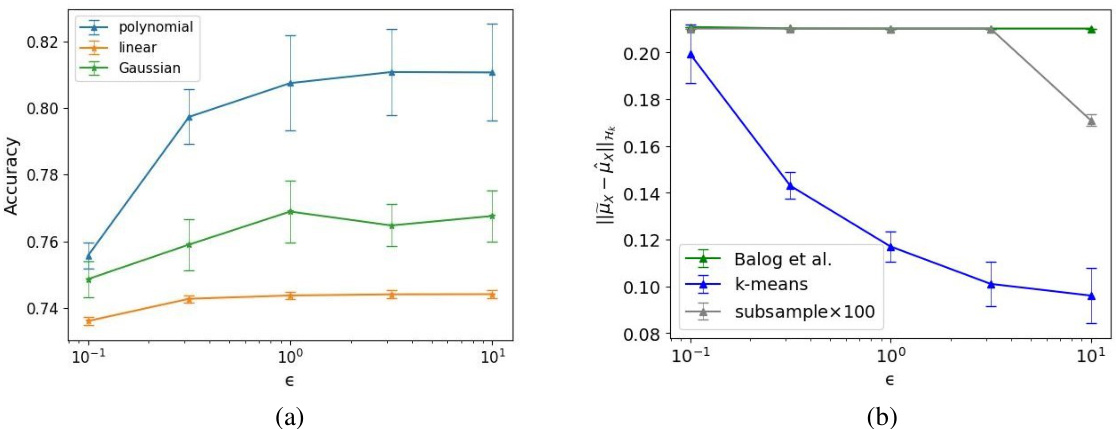
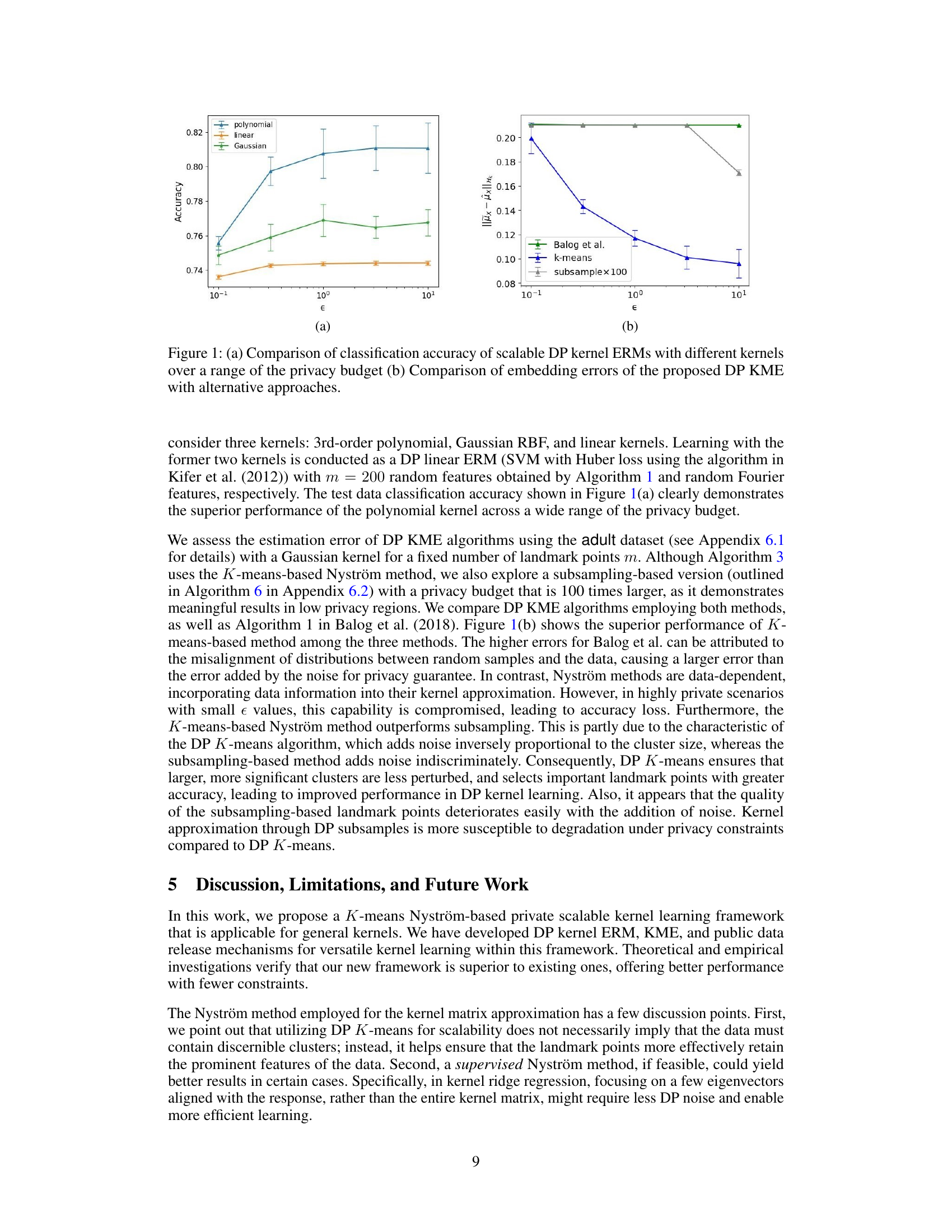
🔼 Figure 1(a) compares the classification accuracy of three different scalable differentially private (DP) kernel empirical risk minimization (ERM) algorithms using polynomial, linear, and Gaussian kernels, varying the privacy budget (ε). Figure 1(b) compares the embedding errors of three different DP kernel mean embedding (KME) algorithms: the proposed DP KME, DP KME using K-means, and DP KME using subsampling. Both figures showcase the performance of the proposed methods across a range of privacy parameters.
read the caption
Figure 1: (a) Comparison of classification accuracy of scalable DP kernel ERMs with different kernels over a range of the privacy budget (b) Comparison of embedding errors of the proposed DP KME with alternative approaches.

🔼 The table compares four different algorithms for differentially private kernel empirical risk minimization (DP-ERM), focusing on their capabilities regarding general kernels, scalability, test data independence, and general objective functions. It highlights the advantages of the proposed algorithm in addressing limitations present in previous methods.
read the caption
Table 1: Comparison of DP kernel ERM algorithms in terms of restrictions for privacy guarantee.
In-depth insights#
DP Kernel ERM#
Differentially Private (DP) Kernel Empirical Risk Minimization (ERM) tackles the challenge of learning from data while preserving privacy. Traditional ERM methods are vulnerable to privacy breaches, as they directly use sensitive data. DP-ERM introduces carefully calibrated noise to mitigate this risk. The application of DP to kernel methods, known for handling non-linear relationships, introduces new complexities. The key challenge lies in efficiently and accurately approximating the kernel matrix while adding noise. Methods like the Nyström method, using random features, or adding noise directly to the output are common approaches. However, each method presents trade-offs between privacy guarantees, computational efficiency, and accuracy. Scalability is a major concern as kernel methods often involve computationally expensive operations on large kernel matrices. The choice of kernel also impacts the effectiveness of the DP approach, with translation-invariant kernels often being preferred for simpler solutions. Therefore, research in DP-ERM seeks to achieve strong privacy guarantees, accurate model estimation, and scalability, balancing these competing factors.
Nystrom Scalability#
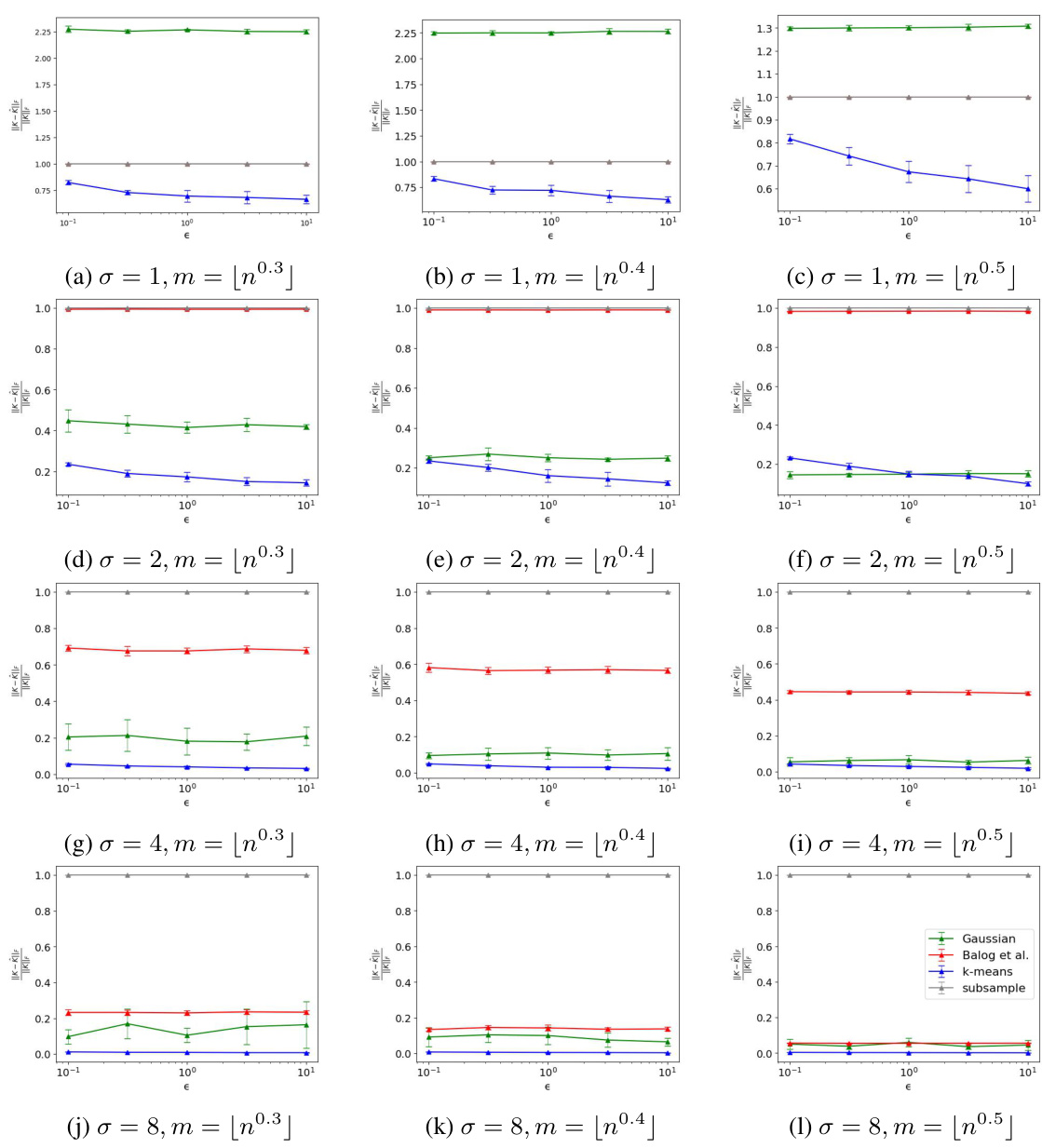
Nyström methods offer a powerful approach to scaling kernel methods by approximating the kernel matrix with a low-rank decomposition. This is particularly beneficial in large-scale machine learning problems where computing and storing the full kernel matrix becomes computationally prohibitive. The core idea is to select a small subset of data points (landmarks) that effectively represent the entire dataset. The kernel matrix is then approximated using only the kernel evaluations between these landmarks and the remaining data points. This approximation significantly reduces the computational complexity, making kernel methods applicable to datasets with millions or even billions of samples. However, the accuracy of the Nyström approximation depends heavily on the choice of landmarks and the kernel function itself. Poor landmark selection can lead to inaccurate approximations and degrade model performance. Several techniques exist for choosing landmarks, such as random sampling, k-means clustering, and more sophisticated approaches that leverage the kernel structure. The trade-off between computational efficiency and approximation accuracy is a central consideration when using Nyström methods. Furthermore, applying Nyström techniques to differentially private (DP) settings adds another layer of complexity. Strategies for ensuring both scalability and privacy preservation are crucial for real-world DP kernel learning applications.
DP KME Release#
Differentially Private Kernel Mean Embedding (DP-KME) release mechanisms aim to privately release information about the distribution of a dataset. This is a crucial problem in machine learning, where releasing raw data poses significant privacy risks. The challenge lies in finding a balance between utility and privacy. DP-KME methods aim to preserve the essential properties of the kernel mean embedding while adding noise to prevent sensitive information leakage. Scalability is a key concern, as DP-KME algorithms need to be efficient enough to handle large datasets. The choice of the underlying kernel significantly impacts performance. Furthermore, theoretical guarantees are essential, providing mathematical bounds on privacy and accuracy. Existing methods often face limitations in terms of scalability, and the generality of kernels they can support. Therefore, new approaches focus on addressing these limitations by using techniques like Nyström methods, offering improvements in both theoretical guarantees and practical efficiency for releasing DP-KME data.
Versatile DP ERM#
The concept of “Versatile DP ERM” suggests an algorithm for differentially private empirical risk minimization (DP-ERM) that is adaptable to a wide range of loss functions and model complexities, unlike traditional DP-ERM methods often limited to specific loss functions or model types. A versatile approach would likely leverage techniques that allow it to handle non-convex or non-smooth loss functions, as well as high-dimensional data. This could involve advanced optimization strategies or clever noise-addition mechanisms to maintain privacy guarantees while achieving good generalization performance across diverse tasks. Such versatility is crucial for practical applications, where the choice of loss function and model structure is often problem-dependent and cannot be pre-determined. Key challenges in designing a versatile DP-ERM algorithm include managing the trade-off between privacy preservation and accuracy across various settings, and ensuring computational efficiency. This is a significant research area with potential for broad impact in various machine learning applications where privacy is a primary concern.
Future Research#
Future research directions stemming from this work on differentially private scalable kernel learning could explore several promising avenues. Extending the framework to handle non-Euclidean data is crucial, perhaps by employing K-medoids instead of K-means for landmark selection. This would broaden the applicability to diverse datasets. Investigating alternative methods for kernel approximation, beyond Nyström, such as those based on random features tailored for specific kernel types, could lead to improved accuracy and efficiency. Developing tighter theoretical bounds for the proposed algorithms and addressing issues arising from non-convex loss functions are also key. Finally, thorough empirical evaluation on a wider variety of real-world datasets across different privacy regimes is essential to solidify the practical impact and robustness of these algorithms.
More visual insights#
More on figures
🔼 Figure 1(a) shows the classification accuracy of three different scalable DP kernel ERMs (polynomial, Gaussian RBF, and linear kernels) across a range of privacy budgets (epsilon). Figure 1(b) compares the embedding errors of the proposed DP KME algorithm against alternative DP KME approaches, illustrating its superior performance.
read the caption
Figure 1: (a) Comparison of classification accuracy of scalable DP kernel ERMs with different kernels over a range of the privacy budget (b) Comparison of embedding errors of the proposed DP KME with alternative approaches.
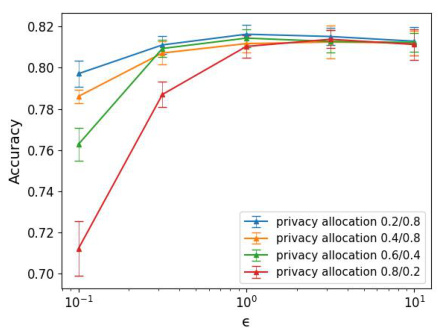
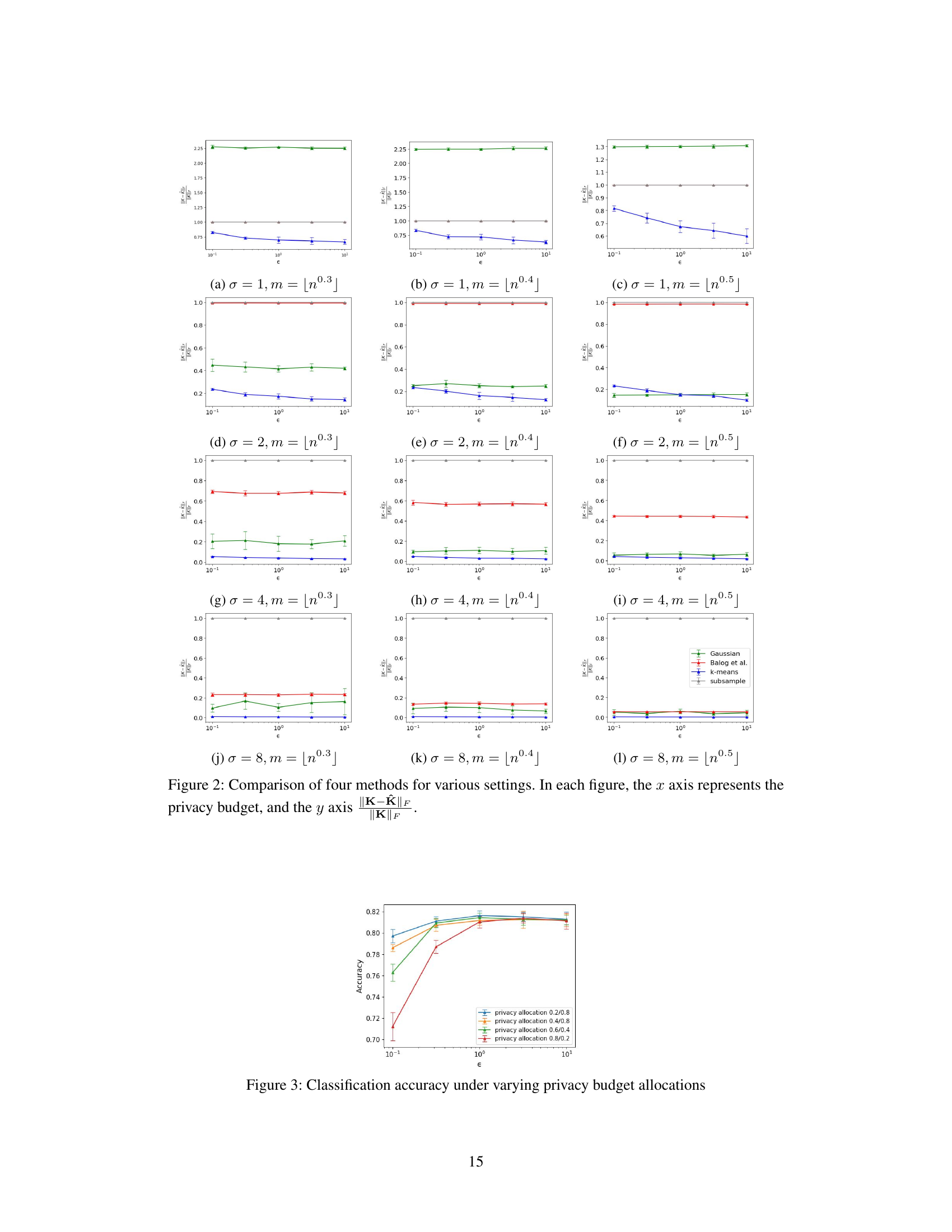
🔼 This figure shows the classification accuracy achieved by the proposed DP kernel ERM algorithm under different privacy budget allocations. The x-axis represents the privacy budget (epsilon), while the y-axis represents the classification accuracy. Different lines represent different allocations of the privacy budget between the DP K-means Nyström approximation (feature map) and the DP linear ERM solver. The plot illustrates how varying the proportion of the privacy budget allocated to each stage impacts the overall accuracy.
read the caption
Figure 3: Classification accuracy under varying privacy budget allocations
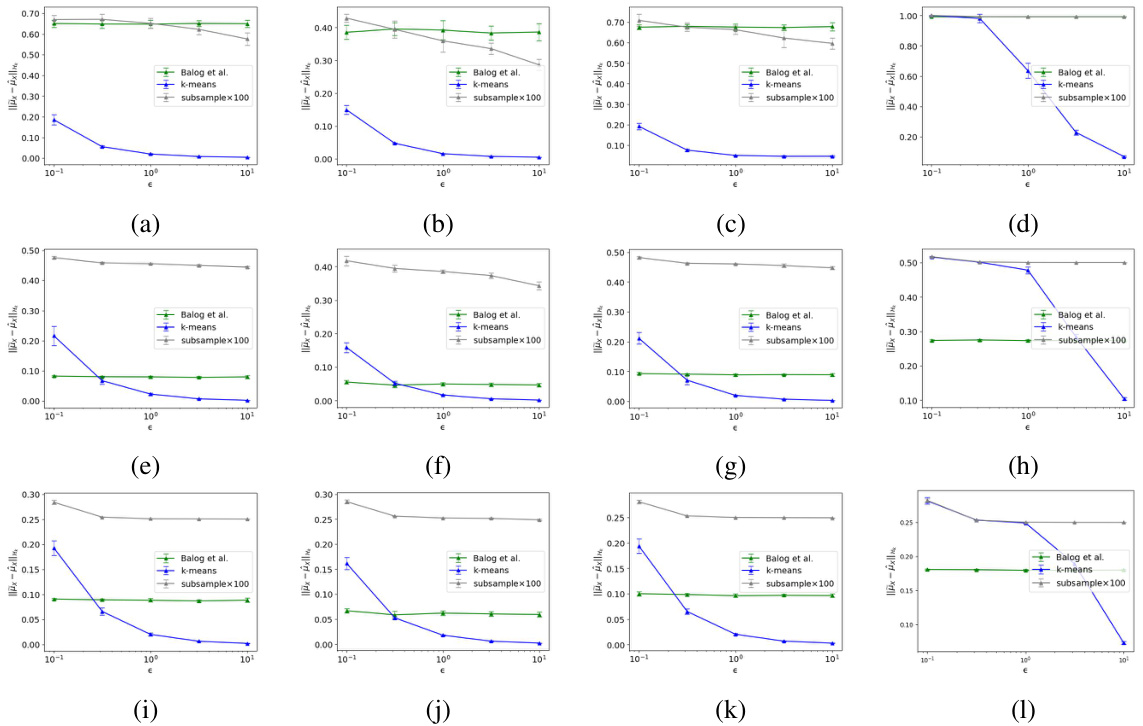
🔼 Figure 1(a) shows the classification accuracy comparison of three different kernel ERMs (polynomial, Gaussian, and linear) under various privacy budgets (epsilon). The polynomial kernel consistently outperforms others. Figure 1(b) compares the embedding errors of the proposed DP KME algorithm against existing approaches using the adult dataset. The K-means based Nystrom method shows superior performance.
read the caption
Figure 1: (a) Comparison of classification accuracy of scalable DP kernel ERMs with different kernels over a range of the privacy budget (b) Comparison of embedding errors of the proposed DP KME with alternative approaches.
Full paper#