TL;DR#
Many research studies utilize data from a source population to infer relationships in a target population. However, differences in data distributions between populations (covariate shift) can invalidate traditional statistical tests like the Conditional Randomization Test (CRT). This poses a significant challenge in making accurate inferences.
This paper introduces a novel method, the Covariate Shift Corrected Pearson Chi-squared Conditional Randomization (csPCR) test, to overcome this challenge. csPCR integrates importance weights to account for covariate shift and employs control variates to improve statistical power. Through theoretical analysis and simulations, the authors show that csPCR maintains accurate Type-I error control while offering superior power compared to existing methods. A real-world application to COVID-19 data further highlights its practical utility.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers dealing with conditional independence testing, particularly in scenarios involving covariate shift. It offers a novel and powerful method (csPCR) to address this critical issue, improving the validity and power of analyses across various fields. The theoretical guarantees and empirical validation provide strong support for its use, while the real-world application demonstrates its practical utility. This work opens new avenues for research in causal inference and robust statistical testing.
Visual Insights#
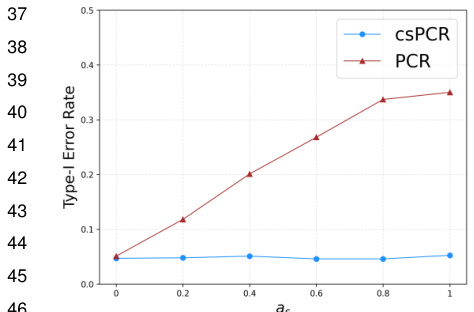
🔼 This figure compares the Type-I error rate of three methods: csPCR, csPCR(pe), and IS across different scenarios. The left panel shows how the Type-I error rate changes with varying sample size used to estimate density ratios, while the right panel shows the Type-I error rate under varying strength of indirect effects. The results demonstrate that csPCR and csPCR(pe) maintain better control over Type-I errors compared to the IS method especially in low sample size scenarios or when density ratio estimations are less accurate.
read the caption
Figure 3: Comparison of Type-I error control across three methods.

🔼 This table presents the p-values obtained from three different methods (csPCR, csPCR(pe), and IS) when applied to a real-world dataset concerning the impact of a COVID-19 treatment on 90-day mortality. The csPCR and csPCR(pe) methods are the proposed methods in the paper, while the IS method serves as a benchmark.
read the caption
Table 1: p-values of different methods on COVID-19 dataset
In-depth insights#
CRT Enhancement#
The heading ‘CRT Enhancement’ suggests improvements to the Conditional Randomization Test (CRT). CRT’s strength lies in its exact Type I error control and flexibility, but it can be limited by covariate shift. Enhancements would likely focus on addressing this limitation, perhaps through weighting techniques (like inverse propensity scoring) to adjust for distributional differences between source and target populations, or by incorporating advanced machine learning methods for more robust conditional independence testing. A further enhancement could be improving the power of CRT while maintaining Type I error control, possibly by leveraging control variates to reduce variance or by incorporating more sophisticated test statistics. Another area of potential focus might be the development of efficient algorithms for CRT, particularly when dealing with high-dimensional data or complex model structures. The goal is to create a more versatile and powerful CRT variant suitable for real-world applications where covariate shift and efficiency considerations are paramount.
Covariate Shift#
Covariate shift, a critical challenge in applying machine learning models trained on one dataset (source) to another (target), is thoroughly investigated in this research. The core issue lies in discrepancies between the distributions of covariates (input variables) in the source and target domains, even when the conditional relationship between the outcome and covariates remains consistent. This discrepancy undermines the validity of standard statistical tests and model predictions. The researchers highlight the limitations of traditional methods when covariate shift is present and propose a novel approach to mitigate its impact. The focus is on adapting the Conditional Randomization Test (CRT) framework to correct for covariate shift, emphasizing the robustness and flexibility of this method. The proposed approach involves integrating importance weights to rebalance the source data and adjust for distributional differences, enhancing both the validity and power of the CRT. Furthermore, the introduction of control variates addresses potential increases in variance associated with importance weighting, leading to improved power. Theoretical justifications and comprehensive simulation studies demonstrate that the proposed methods accurately control Type I errors and maintain superior power even under significant covariate shift. The application of the proposed methodology to real-world data underscores its practical value and the potential implications for various research areas impacted by covariate shift.
csPCR Method#
The csPCR (Covariate Shift Corrected Pearson Chi-squared Conditional Randomization) method is a novel statistical approach designed to address the limitations of traditional conditional randomization tests when faced with covariate shift. It directly incorporates importance weights, derived from the density ratio between source and target populations, to adjust for distributional differences in covariates. This adjustment is crucial for ensuring the validity of inference in the target population, a common challenge when generalizing from source data. The method leverages the control variates method to reduce the variance in the test statistics, enhancing the statistical power. Importantly, the csPCR method maintains control over Type-I errors asymptotically, a crucial property for ensuring reliable inferences. The integration of importance weights and the control variates method positions csPCR as a robust and powerful tool for testing conditional independence, particularly in real-world settings where covariate shift is prevalent. The method’s ability to handle such shifts is a significant advantage over traditional methods, offering enhanced validity and power when generalizing findings. Further, its theoretical grounding and strong empirical validation support its applicability across various domains.
Power & Variance#
The power of a statistical test refers to its ability to correctly reject a false null hypothesis, while variance quantifies the dispersion or spread of the data. In the context of hypothesis testing, high power is desirable as it indicates a greater chance of detecting a true effect, while low variance is preferable because it suggests more precise and reliable results. The relationship between power and variance is complex. Reducing variance generally improves power, making it easier to detect true effects. However, methods to reduce variance might inadvertently reduce the power of the test if they are not carefully designed. For instance, importance weighting methods can increase variance if the weights are too extreme. Therefore, finding the right balance between power and variance is crucial for designing effective statistical tests. The authors’ contributions to this are significant, presenting a methodology that not only maintains Type-I error control but also substantially improves statistical power by addressing covariate shifts while concurrently managing variance via the control variates method. This approach strikes a crucial balance, ensuring both high power and the precision necessary for reliable results.
Real-World Test#
A robust real-world test is crucial for validating the proposed covariate shift corrected conditional randomization test (csPCR). Ideally, it should involve a scenario with a clear treatment variable, well-defined outcome, and a diverse set of confounding factors, reflecting the complexities of real-world data. The choice of dataset is critical, needing sufficient sample size and known distributions of key variables in both source and target populations to allow for accurate assessment of type-I error control and power. The comparison with existing methods, particularly importance sampling methods, is essential to demonstrate the advantages of csPCR in a realistic setting. Analyzing the results requires careful consideration of potential confounding variables and bias. Clear visualizations of the results can help in understanding the test’s efficacy and highlight any limitations encountered during implementation. Ultimately, a successful real-world test can provide compelling evidence of csPCR’s practical utility and enhance its credibility as a valuable tool for causal inference.
More visual insights#
More on figures

🔼 This figure uses two directed acyclic graphs (DAGs) to visually represent the differences in variable relationships between the source and target populations. In the source population (a), we have variables Xs, Vs, and Ys, with ZS as a confounder affecting both Xs and Vs, while Vs affects Ys. In the target population (b), similar variables XT, VT, and YT are presented. The key difference is that the distribution of (X, Z, V) may change between the two populations. This change could affect the relationship between Y and X, especially when conditioning on Z and V. The DAGs highlight how covariate shift might lead to different conditional independence conclusions between the two populations. Even if Y and X are conditionally independent given Z and V in one population, this might not hold true in the other population.
read the caption
Figure 2: Direct acyclic graphs illustrating possible differences between the source and the target populations.
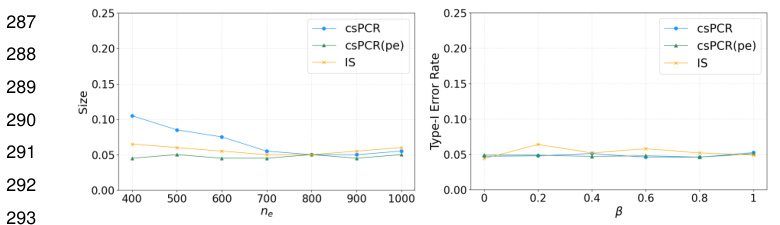
🔼 This figure compares the Type-I error rate of three methods: csPCR, csPCR(pe), and IS. The left panel shows the Type-I error rate as the sample size (ne) used for density ratio estimation increases. The right panel shows the Type-I error rate as the indirect effect size (β) varies. The results demonstrate that csPCR and csPCR(pe) maintain better Type-I error control, especially when the sample size is small or the indirect effect is strong.
read the caption
Figure 3: Comparison of Type-I error control across three methods.
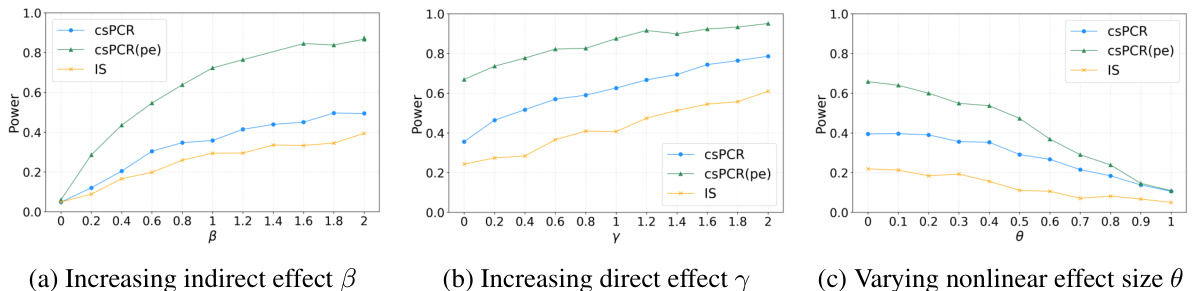
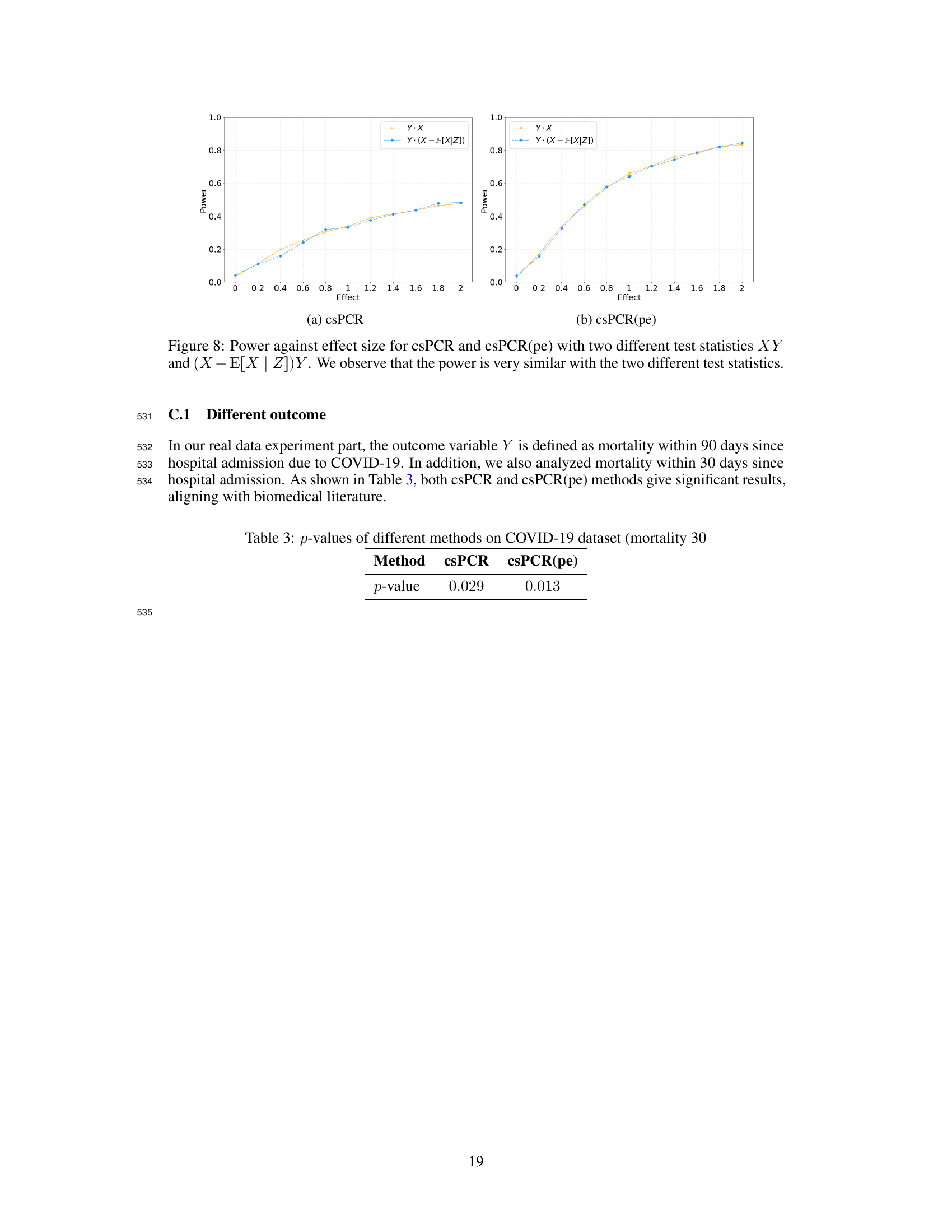
🔼 This figure compares the statistical power of three methods: csPCR, csPCR(pe), and IS, across three scenarios with varying effect sizes. The x-axis in each subplot represents different levels of an effect size (β, γ, or θ), while the y-axis shows the statistical power (probability of correctly rejecting the null hypothesis). The three lines represent the three methods being compared. The figure aims to demonstrate the superior power of the csPCR and its power-enhanced version (csPCR(pe)) compared to the baseline IS method in various scenarios. Subplots illustrate how power changes with indirect effect (β), direct effect (γ), and a nonlinear effect size (θ).
read the caption
Figure 4: Comparison of statistical power of the three methods as the effect size varies: (a) indirect effect β, (b) direct effect γ, and (c) nonlinear effect size θ.
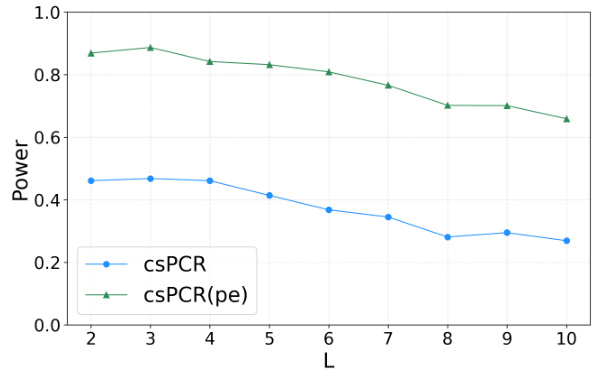
🔼 The figure shows the comparison of statistical power of csPCR and csPCR(pe) methods as the parameter L varies. The x-axis represents the different values of L, and the y-axis shows the corresponding statistical power. The plot displays two lines, one for csPCR and one for csPCR(pe), illustrating how the power of each method changes with different values of L. The figure is used to determine the optimal hyperparameter L for both methods.
read the caption
Figure 5: Comparison of statistical power of the three methods as the the parameter L varies.
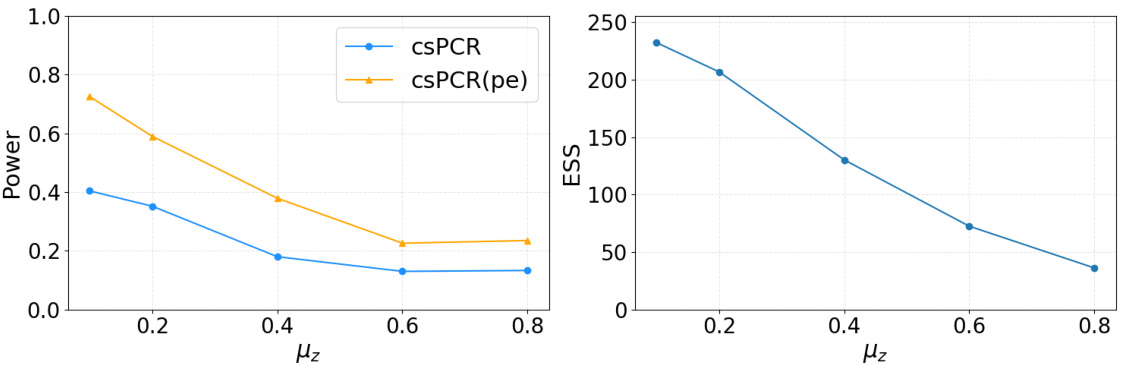
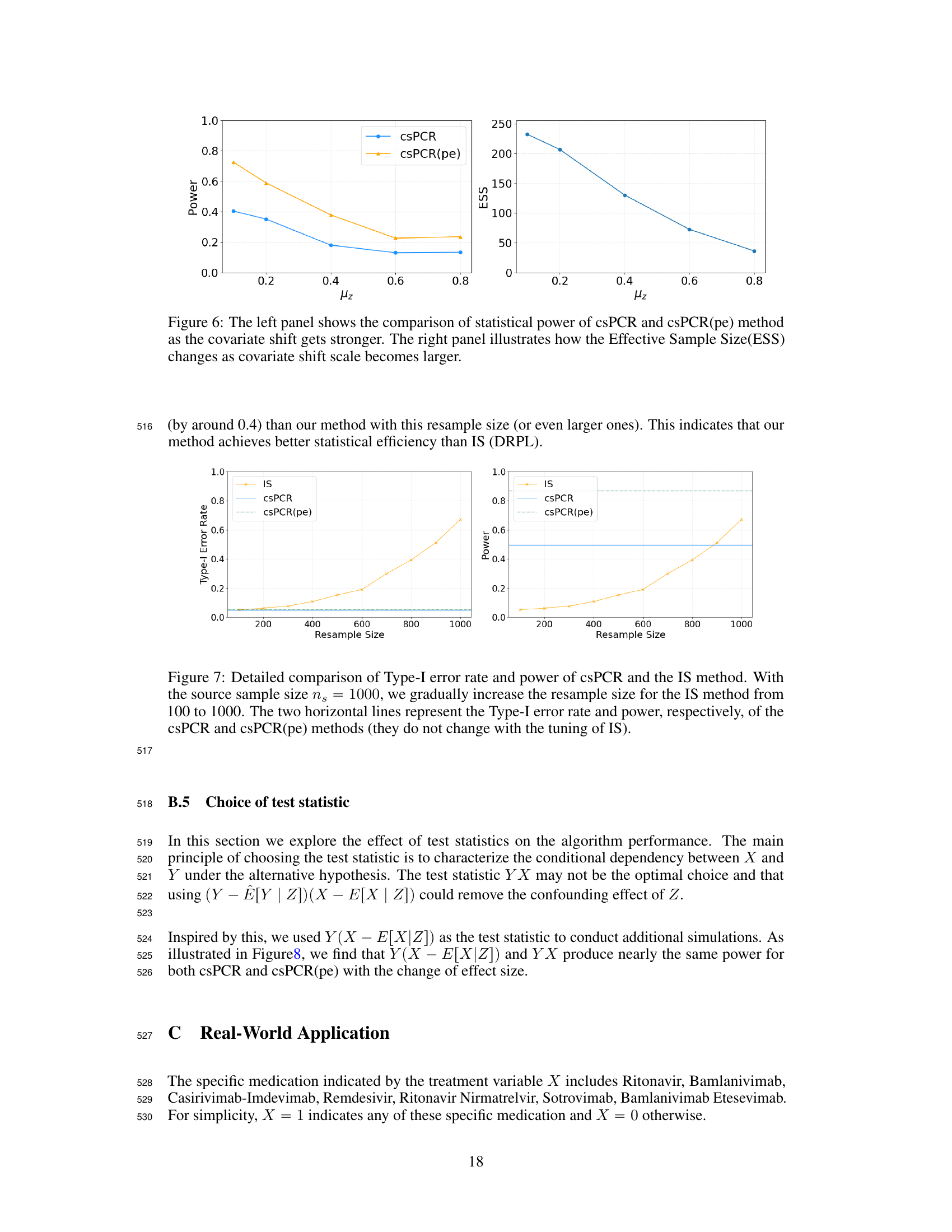
🔼 This figure shows the impact of covariate shift on the statistical power and effective sample size (ESS) of the csPCR and csPCR(pe) methods. The left panel demonstrates that as the covariate shift (measured by μz) increases, the statistical power of both methods decreases, with csPCR(pe) showing a slightly slower decline. The right panel illustrates that the ESS also decreases as the covariate shift strengthens, indicating a reduction in the effective number of samples used in the analysis. This suggests that stronger covariate shift leads to both reduced power and lower ESS, highlighting the challenge posed by covariate shift in statistical analysis.
read the caption
Figure 6: The left panel shows the comparison of statistical power of csPCR and csPCR(pe) method as the covariate shift gets stronger. The right panel illustrates how the Effective Sample Size(ESS) changes as covariate shift scale becomes larger.
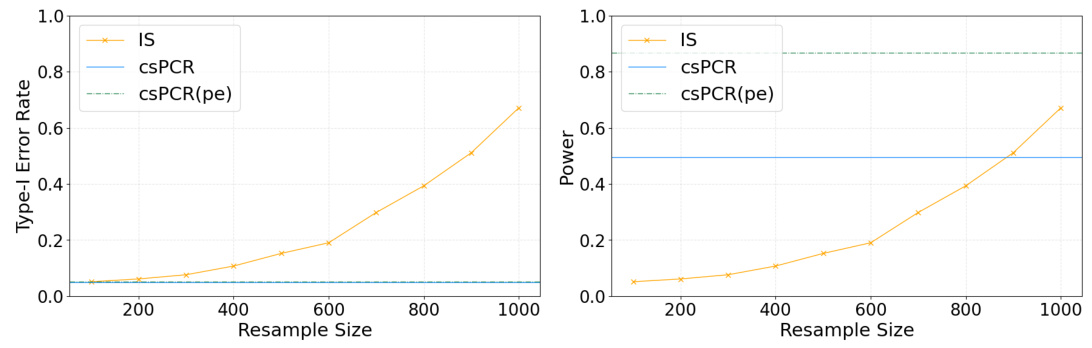
🔼 This figure compares the Type-I error rate of three methods: csPCR, csPCR(pe), and IS across different scenarios. The left panel shows how the Type-I error rate changes as the sample size (ne) used to estimate the density ratio increases, for a fixed value of the indirect effect size (β). The right panel shows how the Type-I error rate changes as the indirect effect size (β) increases, when the density ratio is well-approximated. The results demonstrate that csPCR and csPCR(pe) maintain better Type-I error control, especially when the density ratio is not well approximated or the sample size is small.
read the caption
Figure 3: Comparison of Type-I error control across three methods.
🔼 This figure compares the Type-I error rate of three methods: csPCR, csPCR(pe), and IS across different scenarios. The left panel shows how the Type-I error rate changes with the sample size used for density ratio estimation (ne), demonstrating the stability and control of csPCR and csPCR(pe) even with small sample sizes. The right panel demonstrates that the methods maintain good Type-I error control regardless of the strength of indirect effects (β), and csPCR and csPCR(pe) show more stable control than IS.
read the caption
Figure 3: Comparison of Type-I error control across three methods.
More on tables

🔼 This table presents the Type-I error rates obtained from the csPCR method at various levels of the hyperparameter L. It shows the true density ratio and the estimated density ratio for each L value. This is used to determine the optimal L to balance Type I error and statistical power.
read the caption
Table 2: Type-I Error Rates at Different Levels of L of csPCR Method

🔼 This table presents the p-values obtained from applying three different methods (csPCR, csPCR(pe), and IS) to analyze the association between a COVID-19 treatment and 30-day mortality. The csPCR and csPCR(pe) methods demonstrate statistically significant associations (p<0.05), while the IS method does not. This highlights the increased power and validity of the proposed csPCR methods, particularly under covariate shift conditions.
read the caption
Table 3: p-values of different methods on COVID-19 dataset (mortality 30)
Full paper#