TL;DR#
High-dimensional single index models (SIMs) are powerful tools, but their efficiency suffers from outlying observations and heavy-tailed distributions. Existing inference methods often rely on restrictive distributional assumptions, which limits their applicability in real-world scenarios. The lack of robust and efficient inference procedures creates a significant hurdle in effectively analyzing high-dimensional data sets, especially in various scientific fields where such data is frequently encountered.
This research introduces a robust method to address these limitations by recasting SIMs into pseudo-linear models with transformed responses. This transformation relaxes distributional assumptions, leading to improved efficiency for heavy-tailed errors. The proposed method provides asymptotically honest group inference procedures, which are shown to be highly competitive with existing methods. Additionally, a multiple testing procedure is developed to control the false discovery rate, enhancing the reliability of simultaneous inference. The methodology is supported by both theoretical proofs and numerical experiments, demonstrating its superiority in various conditions.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with high-dimensional data, especially when dealing with outliers or heavy-tailed distributions. It offers robust and efficient methods for inference, advancing the capabilities of single index models and opening new avenues for research in various scientific disciplines. The novel procedures are highly competitive, especially in situations with heavy-tailed errors, improving on existing methods.
Visual Insights#
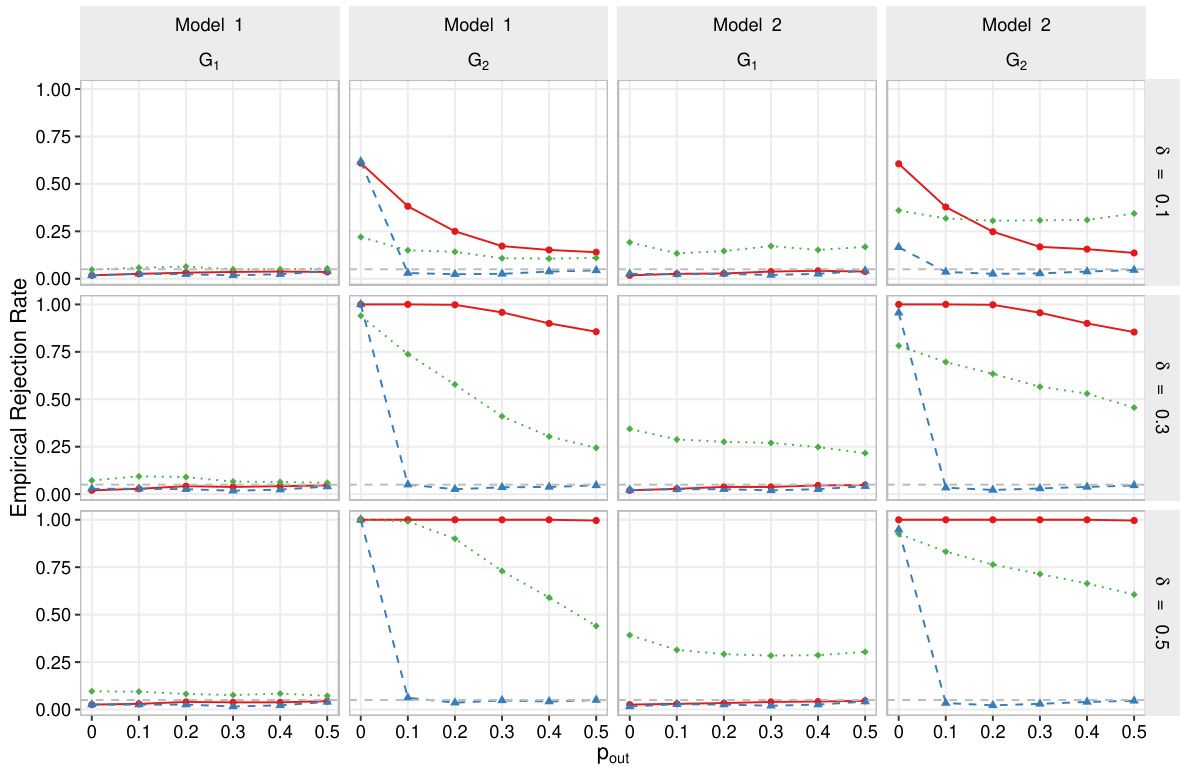
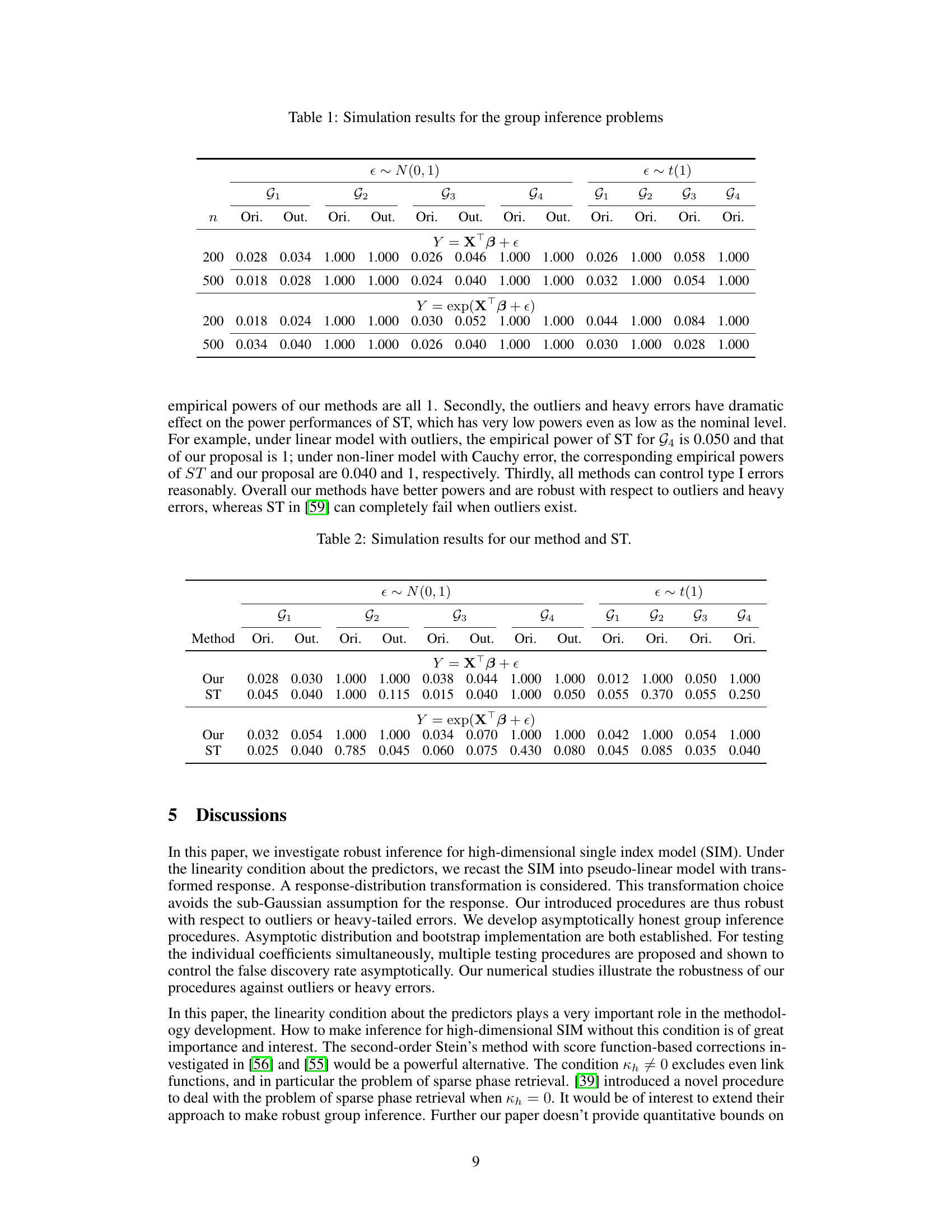
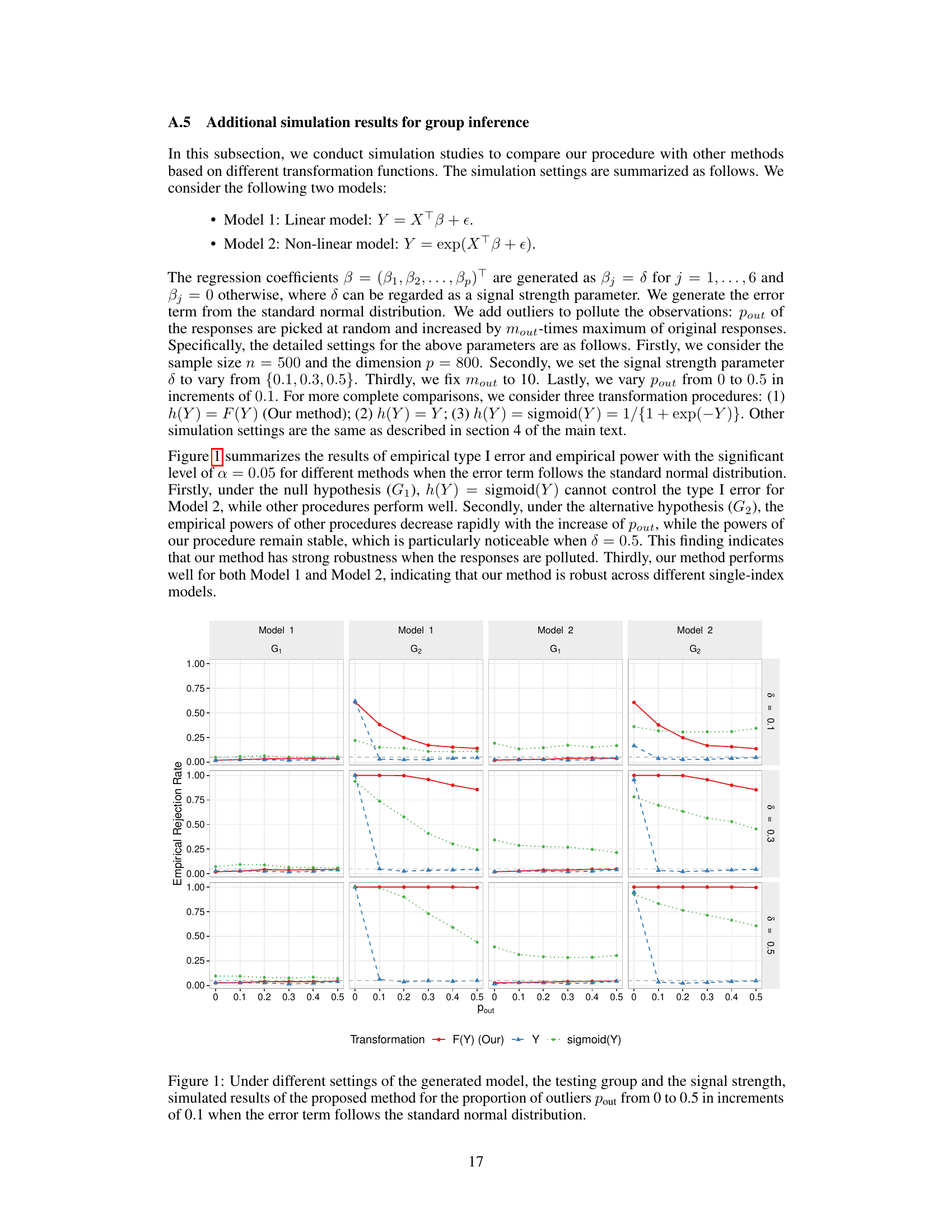
🔼 This figure displays the empirical rejection rates for different settings, including linear and nonlinear models, two group sizes (G1 and G2), three signal strengths (δ = 0.1, 0.3, 0.5), and varying proportions of outliers (pout). The results are based on the standard normal distribution for the error terms. The plot shows how the empirical rejection rate varies across these conditions. The proposed method in the paper is evaluated.
read the caption
Figure 1. Under different settings of the generated model, the testing group and the signal strength, simulated results of the proposed method for the proportion of outliers pout from 0 to 0.5 in increments of 0.1 when the error term follows the standard normal distribution.
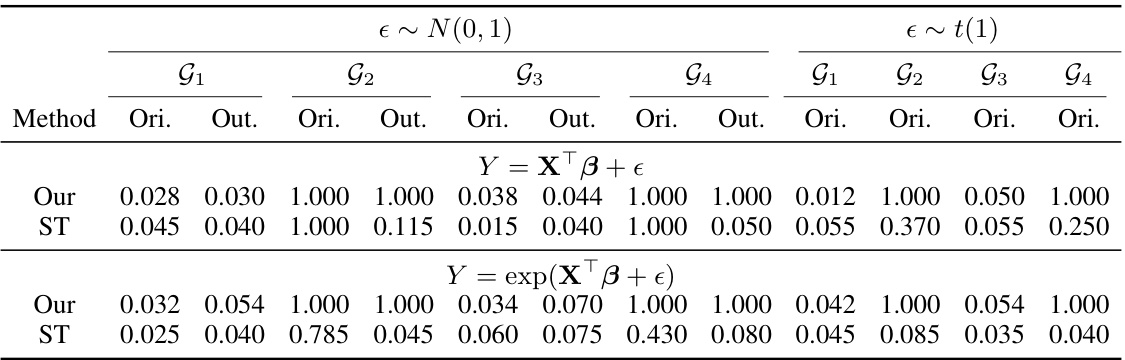
🔼 This table presents the simulation results for the group inference problems. It shows the empirical type I error (for groups G1 and G3, where the true coefficients are all zero) and the empirical power (for groups G2 and G4, where some true coefficients are non-zero) under different scenarios. The scenarios vary based on the sample size (n=200, 500), the dimensionality of predictors (p=800), the presence or absence of outliers, and the error distribution (normal and Cauchy). The results are reported for both linear and non-linear models.
read the caption
Table 1: Simulation results for the group inference problems
Full paper#