DiffPO: A causal diffusion model for learning distributions of potential outcomes

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents DiffPO, a novel and flexible approach to a critical problem in causal inference: learning the distributions of potential outcomes. This method addresses limitations of existing techniques by providing uncertainty quantification and showing state-of-the-art performance across various experiments. It opens doors for more reliable decision-making in fields like medicine, where uncertainty is a key factor. The use of diffusion models provides a new angle of attack that other methods have not explored. The development of an orthogonal diffusion loss function to address selection bias is an important theoretical contribution.

Visual Insights

#

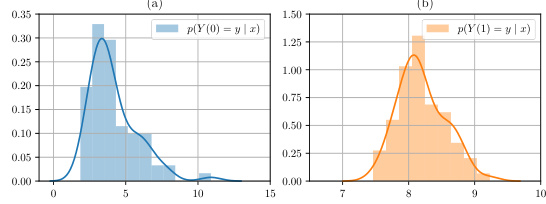
This figure displays the empirical distributions of the conditional potential outcomes learned by DiffPO for a real-world dataset from medicine. The left panel shows the distribution of the potential outcome under no treatment (Y(0) given covariates x), while the right panel shows the distribution of the potential outcome under treatment (Y(1) given covariates x). The distributions illustrate the differences in potential outcomes given the covariates, and it highlights how DiffPO learns complex distributions beyond simple point estimates, enabling more reliable decision-making.

This table provides a comparison of several key methods for conditional average treatment effect (CATE) estimation and potential outcome (PO) prediction. It shows whether each method allows for uncertainty quantification (UQ), addresses selection bias, uses an orthogonal approach, and whether the method is designed specifically for PO prediction. Key limitations of each method are also listed.

In-depth insights

#

Causal Diffusion

#

The concept of “Causal Diffusion” blends two powerful methodologies: causal inference and diffusion models. Causal inference seeks to establish cause-and-effect relationships from observational data, often tackling the challenge of confounding variables. Diffusion models excel at generating data samples by gradually adding and removing noise, capturing complex data distributions. A “Causal Diffusion” approach would likely leverage the strengths of both, potentially using diffusion models to generate counterfactual data (what would have happened under different treatments) to more accurately infer causal effects. This might involve training a diffusion model to understand the data distribution conditional on both treatment and outcome, allowing generation of samples that vary treatment and outcome while respecting causal relationships. Challenges would include ensuring the generated data reflects true causal relationships and not just correlations, and effectively dealing with the high computational cost associated with diffusion models.

Orthogonal Loss

#

The concept of an orthogonal loss function is crucial in causal inference, particularly when dealing with observational data prone to selection bias. Orthogonality ensures that the estimation of causal effects is robust to misspecifications in the nuisance functions, such as the propensity score (the probability of receiving treatment given covariates). A standard loss function might be highly sensitive to errors in these nuisance parameters, leading to biased estimates of causal effects. In contrast, an orthogonal loss function minimizes this sensitivity, thus providing more reliable and robust estimates even when the nuisance functions are imperfectly estimated. This robustness is particularly valuable in real-world applications where perfect knowledge of nuisance functions is unrealistic. The key advantage is that the estimator derived from this type of loss function is less affected by the inaccuracies of estimation of nuisance functions, hence the causal effect estimation is more reliable. The development and application of orthogonal loss functions represent a significant advance in causal inference methodology. It is a powerful tool for achieving more accurate and reliable results in the presence of unavoidable uncertainties present in observational studies.

Distributional POs

#

The concept of “Distributional POs” introduces a significant advancement in causal inference by moving beyond simple point estimates of potential outcomes (POs) to model the entire distribution of POs. This shift is particularly valuable in high-stakes domains like medicine, where understanding the uncertainty inherent in predictions is crucial for reliable decision-making. Modeling distributional POs provides a richer, more informative picture than point estimates alone, allowing for a more nuanced assessment of risk and benefit associated with different interventions. It enables the quantification of uncertainty, crucial for calculating confidence intervals and making informed decisions in the presence of variability. Furthermore, the ability to sample from the learned distribution allows for exploration of various potential outcomes and the generation of predictive intervals, offering a much more comprehensive understanding than simple average treatment effects. This approach is especially relevant where the variability itself might be clinically significant, impacting treatment choices beyond the simple average effect. The research on “Distributional POs” therefore represents a crucial step towards more robust and reliable causal inference.

Bias Addressing

#

Addressing bias in research is crucial for ensuring reliable and generalizable results. Selection bias, a common issue in observational studies, arises when treatment assignment isn’t random, leading to differences between treatment and control groups that are not solely due to the treatment itself. This makes it difficult to isolate the treatment’s true effect. The paper tackles this directly by proposing novel methods to account for the covariate shift. This likely involves techniques to either re-weight data points, creating a balanced representation that minimizes the effect of non-random assignment, or adjusting the learning algorithm to explicitly model and correct for the biases caused by the differing distributions. Successfully addressing selection bias enhances the credibility of causal inferences, ensuring that the observed effects can be attributed to the intervention and not confounding factors associated with non-random selection. Further, the robustness of these methods under model misspecification is also important, emphasizing the importance of the orthogonal diffusion loss to reduce sensitivity to inaccurate model assumptions. A comprehensive approach to bias addressing is essential to achieve accurate estimations of potential outcomes and build more reliable causal models.

Future Research

#

Future research directions stemming from this work on causal diffusion models for potential outcome prediction could explore several avenues. Improving the efficiency of the sampling process is crucial, potentially through advancements in diffusion model solvers or one-step sampling techniques. Extending the model’s flexibility to handle various data types and more complex causal relationships (e.g., time-series data, multiple treatments) would broaden its applicability. Addressing the limitations posed by strong assumptions (e.g., unconfoundedness, overlap) is vital for increasing the model’s robustness in real-world scenarios where these assumptions might not hold perfectly. Developing novel loss functions or leveraging advanced techniques to address selection bias more effectively could further enhance the accuracy and reliability of estimates. Investigating the model’s behavior under various data characteristics and noise levels is key to understanding its limitations and strengths. Finally, rigorous empirical evaluation on a larger and more diverse set of real-world datasets is needed to fully assess its generalizability and practical performance in clinical decision-making.

More visual insights

#

More on tables

This table compares various methods for estimating Conditional Average Treatment Effects (CATE) and predicting potential outcomes (POs). It highlights key differences between the methods in terms of their ability to quantify uncertainty in POs, address selection bias, and utilize orthogonal properties for robustness. It also indicates whether each method was originally designed for PO prediction or primarily focuses on CATE estimation. The table is useful in understanding the strengths and limitations of existing approaches and motivating the need for a new method that addresses shortcomings, such as uncertainty quantification and selection bias.

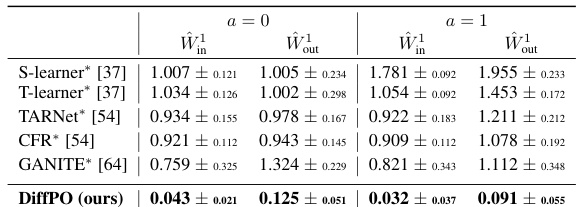
This table presents the in-sample and out-of-sample Wasserstein distances (W1 metric) for two different potential outcomes (a=0 and a=1) across multiple methods. Lower values indicate better performance in learning the distribution of potential outcomes. The results are averaged over 10 train-test splits on a synthetic dataset.

This table presents the results of evaluating the uncertainty estimation of the two potential outcomes (a=0 and a=1) using different methods. The results are reported as the mean ± standard deviation over ten-fold train-test splits. The table shows the empirical coverage of 95% and 99% prediction intervals (PIs) generated by each model. Higher values indicate better uncertainty quantification.

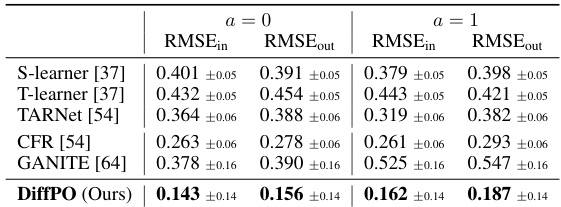
This table presents the results of point estimation for potential outcomes (POs) using different methods. It compares the root mean squared error (RMSE) for both in-sample and out-of-sample predictions on a synthetic dataset. The RMSE is calculated for each of the two potential outcomes (a=0 and a=1), which correspond to different treatments. Lower RMSE values indicate better performance. The results are averaged across ten-fold train-test splits and reported with standard deviations.

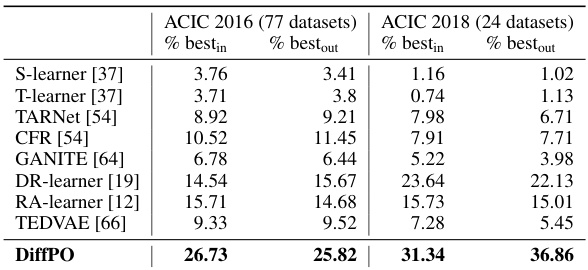
This table presents the performance comparison of different methods for learning the distributions of potential outcomes (POs) using the Wasserstein distance metric. The table shows the in-sample (Win) and out-of-sample (Wout) Wasserstein distances for predicting potential outcomes under treatment (a=1) and control (a=0) conditions. The results are averaged over ten different train-test splits of the synthetic dataset, providing a robust evaluation of the methods’ performance.

Full paper

#