TL;DR#
Neural networks learn data representations residing on low-dimensional manifolds, but comparing these spaces remains challenging. Existing methods are either complex, lack interpretability, or are sensitive to noise. This necessitates efficient, robust methods for comparing and aligning these spaces to enhance performance in downstream tasks such as retrieval and data transfer across various modalities.
This paper introduces Latent Functional Maps (LFM), a novel spectral framework that tackles these issues. LFM leverages spectral geometry principles in the functional domain, boosting both interpretability and performance. The framework is shown to efficiently compare spaces, find correspondences (even with limited data), and transfer information between them. Evaluations across diverse applications and modalities showcase LFM’s efficacy and robustness, surpassing existing methods in many aspects.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in representation learning and computer vision as it offers a novel framework for comparing and aligning representations across different neural networks. It is particularly important due to its versatility in handling various applications and modalities, its robustness to noise and perturbations, and its ability to improve downstream task performance. This research opens new avenues for zero-shot learning, efficient model adaptation, and enhanced interpretability of neural network representations.
Visual Insights#
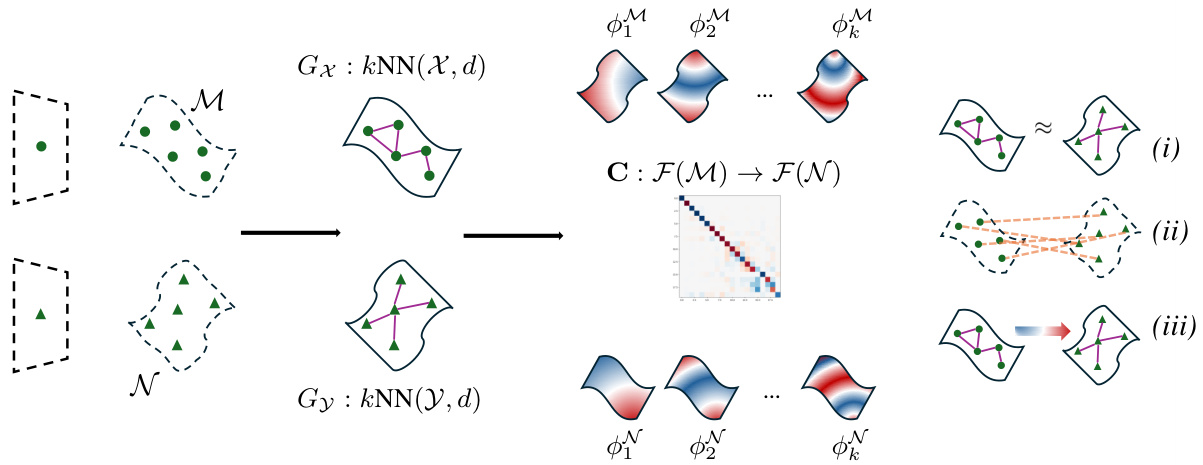
🔼 This figure provides a high-level overview of the Latent Functional Maps (LFM) framework. It shows how two datasets X and Y, represented as manifolds M and N, are approximated using k-Nearest Neighbor (kNN) graphs. A latent functional map C is then learned to align the eigenbases of the graph Laplacian operators defined on these graphs. This map facilitates (i) comparing the representational spaces, (ii) solving correspondence problems between them, and (iii) transferring information between the spaces.
read the caption
Figure 1: Framework overview: given two spaces X, Y their samples lie on two manifolds M, N, which can be approximated with the KNN graphs Gx,Gy. We can optimize for a latent functional map C between the eigenbases of operators defined on the graphs. This map serves as a map between functions defined on the two manifolds and can be leveraged for (i) comparing representational spaces, (ii) solving correspondence problems, and (iii) transferring information between the spaces.

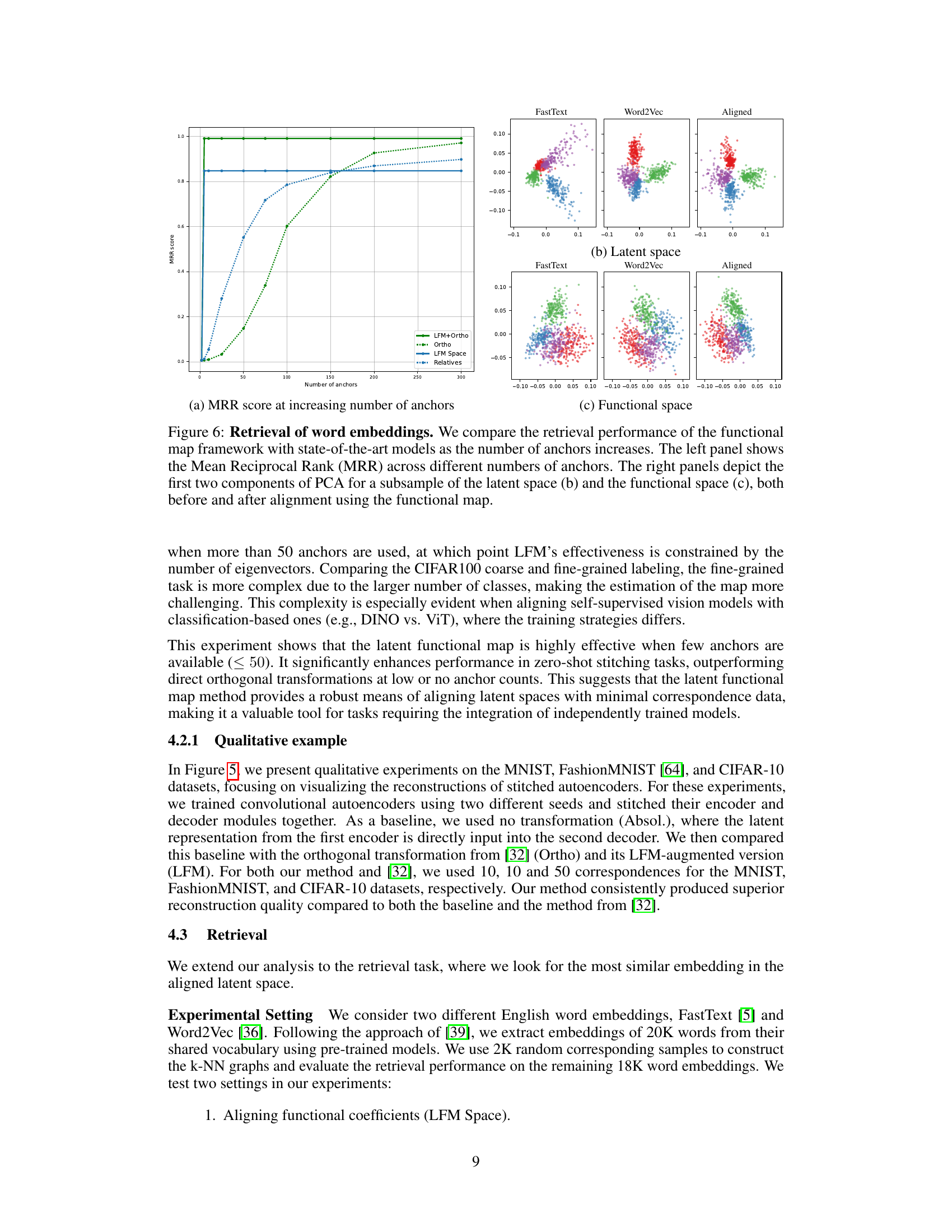
🔼 This table presents the Mean Reciprocal Rank (MRR) scores for a word embedding retrieval task using different methods. It compares the performance of the proposed Latent Functional Map (LFM) approach against baseline methods like Relative [39], Orthogonal transformation [32], Linear, and Affine transformations, assessing their retrieval accuracy with varying numbers of anchors.
read the caption
Table 2: MRR Score for the retrieval of word embeddings. We report the value of the results depicted in Figure 6 adding more kind transformation between spaces (Orthogonal, Linear and Affine).
In-depth insights#
Latent Space Mapping#
Latent space mapping is a crucial technique in machine learning that focuses on establishing relationships between different feature spaces, often learned by neural networks. It tackles the challenge of aligning these spaces, which may represent data in distinct yet potentially related ways. This alignment is critical for various tasks, such as transfer learning, where knowledge gained in one domain is applied to another, and multimodal learning, which integrates information from multiple sources. Effective latent space mapping can improve model performance, enhance interpretability, by revealing underlying connections between feature representations, and enable seamless integration of models. The core of the approach involves learning a mapping function, often via techniques like spectral methods or deep learning-based approaches, which minimizes differences and maximizes similarities between features in the source and target spaces. The choice of mapping function and the optimization strategy employed significantly affect the effectiveness of latent space mapping, thus demanding careful consideration and selection based on data characteristics and task requirements. Successfully aligning latent spaces unlocks the potential for enhanced data analysis and model generalization.
Spectral Alignment#
Spectral alignment, in the context of representation learning, aims to harmonize disparate feature spaces by leveraging their spectral properties. This involves representing data as points on manifolds and utilizing techniques like Laplacian Eigenmaps or diffusion maps to capture the underlying geometry. The core idea is to align the spectral signatures of these manifolds, effectively mapping functions between spaces. This approach facilitates both the comparison of different representation spaces and the transfer of information across them. Latent Functional Maps (LFMs), as described in the research paper, offers a powerful framework for this task. It goes beyond comparing pointwise similarities to modeling relationships between function spaces. LFMs achieve robust performance, even under challenging conditions, enabling tasks such as zero-shot stitching and improving downstream tasks’ accuracy. The interpretability of LFMs is another key advantage, allowing for detailed analysis of the alignment process and potential mapping inconsistencies.
LFM Similarity#
The concept of ‘LFM Similarity’ introduces a novel approach to quantify the similarity between different representational spaces learned by neural networks. Instead of focusing solely on comparing individual data points across spaces, LFM Similarity leverages functional maps to compare the spaces of functions defined on the manifolds representing these data points. This shift allows for a more comprehensive and robust comparison, capturing the intrinsic geometric properties of the spaces. The core idea is that a high degree of similarity indicates the presence of an isometry between the manifolds, which implies that the spaces are fundamentally equivalent in terms of their geometric structure. This offers a substantial advantage over existing methods, such as CKA, which are shown to be sensitive to certain transformations that preserve linear separability but not necessarily geometric structure. The method’s robustness to perturbations is significant. LFM similarity assesses similarity using the functional map (C), specifically examining the properties of C^TC. Its ability to act as a proper distance metric further enhances its use as a powerful tool for analyzing and comparing neural representations. The framework not only quantifies similarity but also provides interpretable insights into the nature and location of any discrepancies or distortions between the compared spaces.
Zero-Shot Stitching#
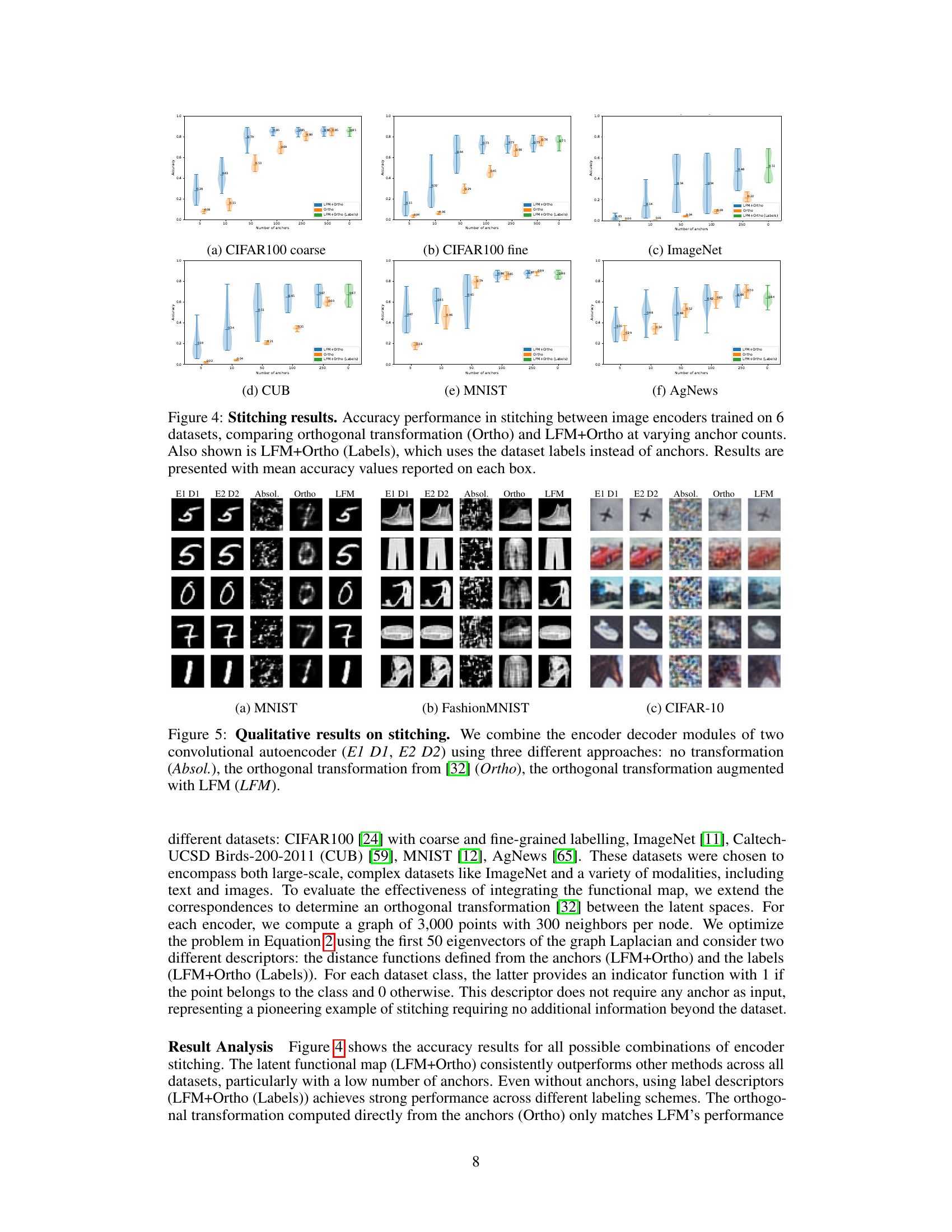
Zero-shot stitching, as explored in the context of this research, presents a compelling approach to integrating distinct neural network components without the need for additional training. This technique directly addresses the challenge of aligning and combining latent spaces from different models, potentially unlocking the ability to leverage the strengths of multiple architectures for a unified task. The key innovation lies in the ability to bridge disparate representational spaces efficiently, a feat accomplished through innovative techniques like functional maps and careful descriptor design. This allows the seamless integration of encoders and decoders trained independently, even with different datasets or modalities, greatly expanding the flexibility of neural network design. The method’s robustness to variations in anchor points and its capability to function effectively with limited supervision is particularly notable. While further research may be needed to assess the technique’s full scope, initial findings demonstrate promising results, showing potential to enhance performance in downstream tasks and provide a powerful, efficient methodology for neural network integration. The success of zero-shot stitching hinges on effectively modeling the underlying mapping between function spaces, bypassing the complexities associated with direct sample-based alignment.
Future of LFMs#
The future of Latent Functional Maps (LFMs) appears bright, given their demonstrated versatility in aligning and comparing representational spaces of neural networks. Further research should explore applications beyond image and text modalities, potentially including audio, video, and even more abstract data types. Improving efficiency and scalability remains a key goal; although the current method is efficient, optimizations could further enhance its applicability to massive datasets. Addressing the reliance on anchors is another crucial area: developing more robust, unsupervised, or weakly-supervised methods for correspondence discovery will significantly broaden the scope of LFMs. A deeper theoretical understanding of the properties and limitations of LFMs, particularly in non-isometric scenarios, would deepen their value as a tool for understanding and comparing neural representations. Finally, investigating the potential for integration with other representation learning techniques, to create a hybrid approach that combines the strengths of LFMs with complementary methods, would unlock further innovation in this field.
More visual insights#
More on figures
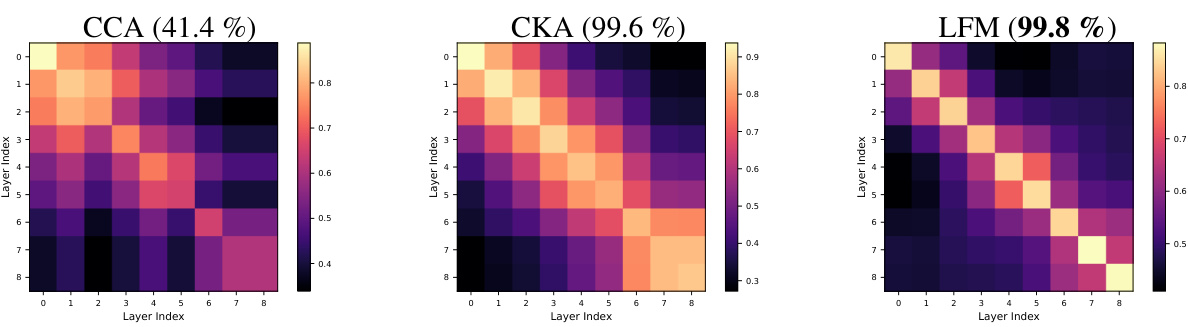
🔼 This figure compares three different methods (CCA, CKA, and LFM) for measuring the similarity between the internal layer representations of 10 different CIFAR-10 trained CNN models. Each method produces a similarity matrix showing the pairwise similarity between layers across the models. The accuracy of each method in correctly matching corresponding layers across the models is reported as a percentage.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.
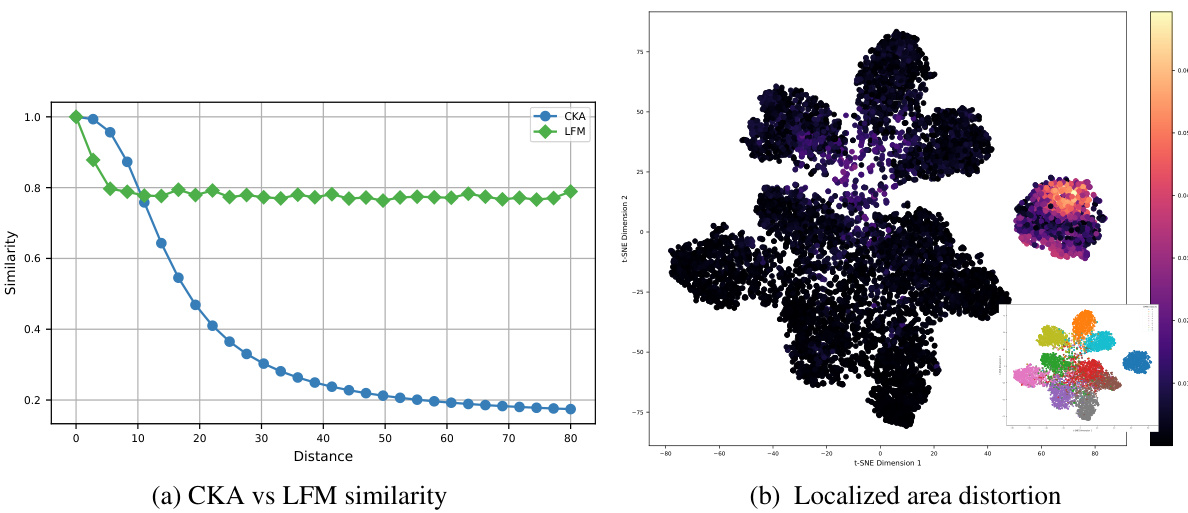
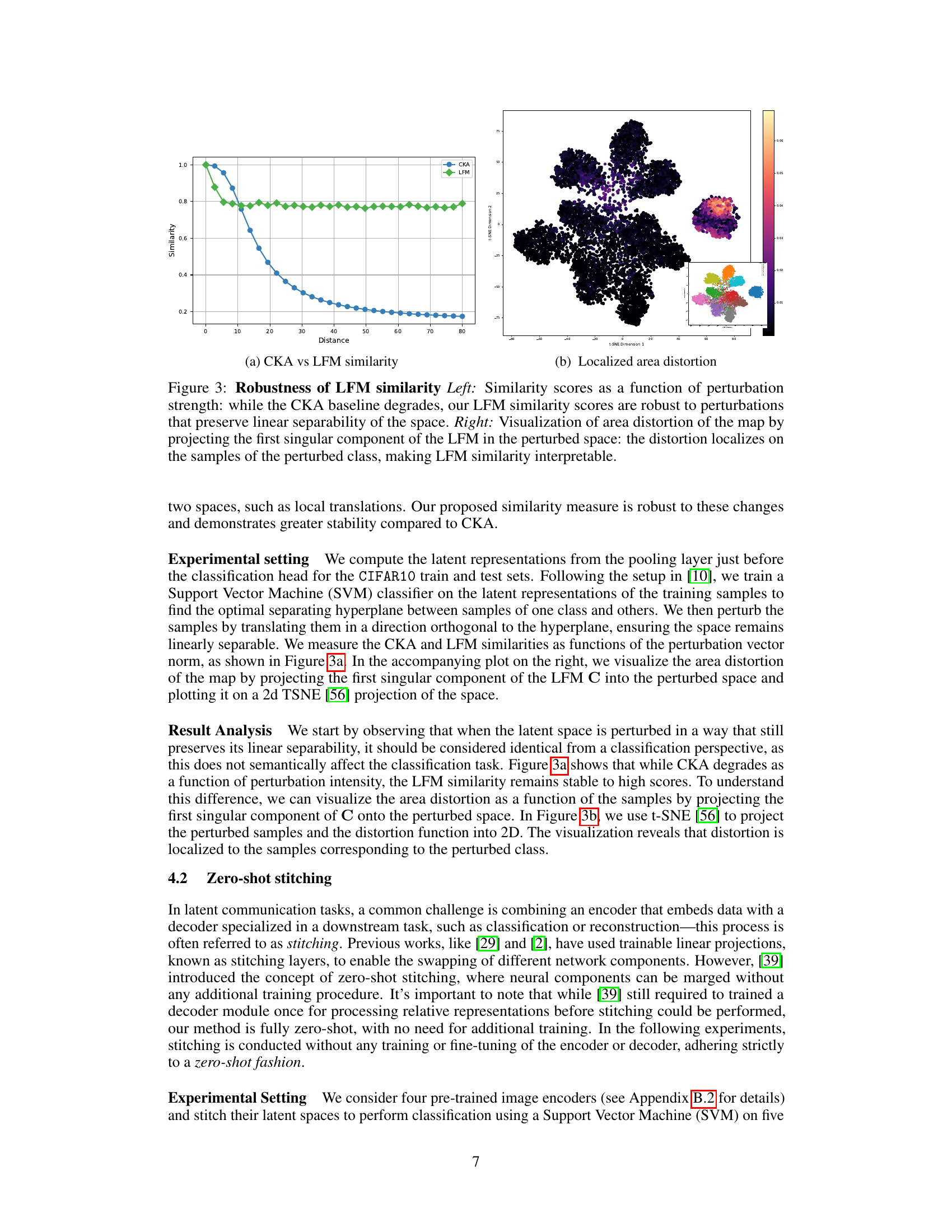
🔼 This figure demonstrates the robustness of the proposed Latent Functional Map (LFM) similarity measure compared to Centered Kernel Alignment (CKA). The left panel shows that LFM similarity remains stable even with significant perturbations to the latent space that preserve linear separability, unlike CKA which degrades. The right panel visualizes the area distortion caused by perturbations, showing that the distortion is localized to specific classes, making the LFM similarity measure more interpretable.
read the caption
Figure 3: Robustness of LFM similarity Left: Similarity scores as a function of perturbation strength: while the CKA baseline degrades, our LFM similarity scores are robust to perturbations that preserve linear separability of the space. Right: Visualization of area distortion of the map by projecting the first singular component of the LFM in the perturbed space: the distortion localizes on the samples of the perturbed class, making LFM similarity interpretable.

🔼 This figure compares the performance of three different methods (LFM, CCA, and CKA) in identifying corresponding layers across multiple models trained on the CIFAR-10 dataset. Similarity matrices are generated for each model, showing the similarity between different layers. The accuracy of each method in matching layers based on similarity scores is presented.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.

🔼 This figure compares the performance of three different methods (CCA, CKA, and LFM) in measuring the similarity between internal layer representations of CIFAR10 across 10 different models. Each method produces a similarity matrix showing pairwise similarity between layers. The accuracy of each method in correctly matching corresponding layers across different models is reported. The visualization helps in assessing which method best captures the representational similarity across different models.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.

🔼 This figure compares the performance of three methods (LFM, CCA, and CKA) in determining the similarity between the internal layer representations of 10 different CIFAR-10 trained CNN models. The similarity matrices visualize the relationships between layers across different models. Accuracy scores, representing the ability to correctly match corresponding layers based on similarity, are reported for each method. The visualization and accuracy scores demonstrate the effectiveness of LFMs compared to CCA and CKA in capturing similarity between layers in different models.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.

🔼 This figure compares the similarity of internal layer representations across 10 different CIFAR-10 trained CNN models using three methods: CCA, CKA, and the proposed LFM method. The similarity is represented as matrices, where each cell shows the similarity between a specific layer in one model and a layer in another model. The accuracy of matching corresponding layers based on maximal similarity is reported for each method. The LFM method shows notably higher accuracy indicating its effectiveness in measuring the similarity between neural network representations.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.

🔼 This figure compares the similarity between the internal layer representations of 10 different CIFAR-10 CNN models using three different methods: CCA, CKA, and the proposed LFM method. The similarity is visualized as a matrix where each entry represents the similarity between corresponding layers from two models. The accuracy of matching layers based on maximal similarity is reported for each method. The LFM method demonstrates higher accuracy compared to CCA and CKA, indicating better performance in capturing the similarity between layer representations across different models.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.
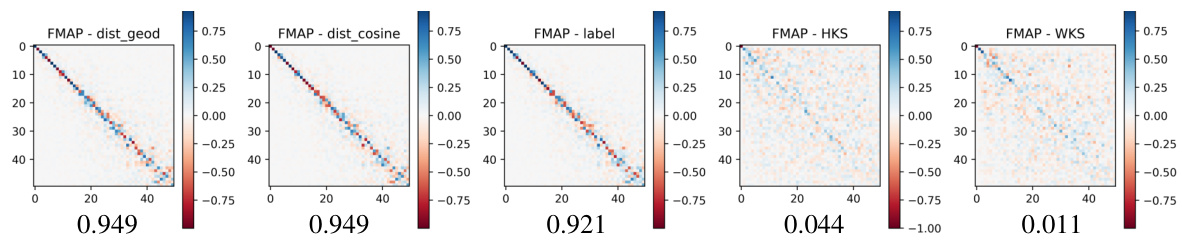
🔼 This figure visualizes how the structure of functional maps changes under increasing levels of noise applied to MNIST embeddings. Two different graph construction methods (using angular and L2 distances) are compared, and the resulting functional maps are shown along with their Mean Reciprocal Rank (MRR) and Latent Functional Map (LFM) similarity scores. The results illustrate the robustness (or lack thereof) of each approach to noisy data.
read the caption
Figure 7: Functional maps structure at increasing level noise. Given a set of MNIST embeddings, we plot the degradation of the functional map structure as the space is perturbed. We compare the graph built with two different metrics (Angular, L2) and report MRR and LFM similarity score.

🔼 This figure compares the similarity between internal layer representations of 10 different CIFAR-10 models using three methods: LFM, CCA, and CKA. The similarity matrices visualize the pairwise similarity between corresponding layers across the models. The caption also highlights that the accuracy of matching corresponding layers based on maximal similarity is reported for each method. LFM demonstrates higher accuracy than CCA and nearly perfect accuracy compared to CKA.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.

🔼 This figure compares the similarity of internal representations across different layers of 10 different CIFAR-10 trained CNN models using three different methods: CCA, CKA, and the proposed LFM method. Each method’s similarity is represented as a matrix where each entry corresponds to the similarity between the same layer in two different models. The accuracy of each method in correctly matching corresponding layers is also reported.
read the caption
Figure 2: Similarity across layers Similarity matrices between internal layer representations of CIFAR10 comparing our LFM-based similarity with the CCA and CKA baselines, averaged across 10 models. For each method, we report the accuracy scores for matching the corresponding layer by maximal similarity.
More on tables
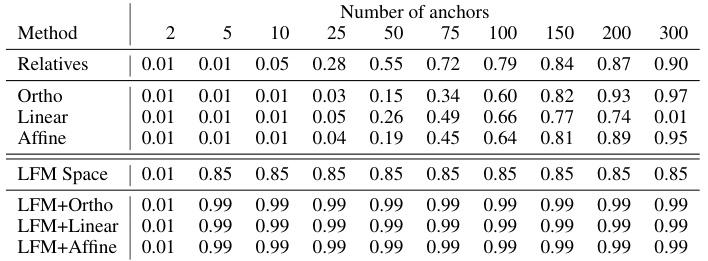
🔼 This table presents the Mean Reciprocal Rank (MRR) scores for word embedding retrieval experiments using different methods. The methods compared include a baseline (Relatives), orthogonal transformation (Ortho), linear transformation (Linear), and affine transformation (Affine). The MRR scores are shown for varying numbers of anchors used in the retrieval process, demonstrating the impact of different transformation methods and anchor counts on retrieval accuracy.
read the caption
Table 2: MRR Score for the retrieval of word embeddings. We report the value of the results depicted in Figure 6 adding more kind transformation between spaces (Orthogonal, Linear and Affine).
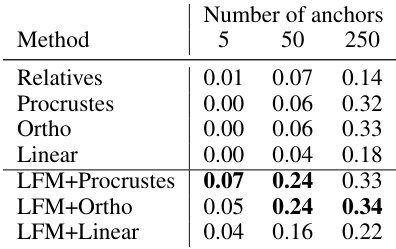
🔼 This table shows the Mean Reciprocal Rank (MRR) scores for different retrieval methods on the CUB dataset. It compares the performance of the proposed Latent Functional Map (LFM) approach against various baselines, including the Relative method from [39], orthogonal transformation from [32], linear transformation, and the Procustes method from [29]. The comparison highlights the effectiveness of LFM in improving retrieval accuracy, especially with a small number of anchors.
read the caption
Table 3: MRR Score for the retrieval of CUB. We report the results on the CUB including the additional baseline Procustes [29].
Full paper#