TL;DR#
This paper tackles the challenge of transfer learning, where a model trained on one dataset is adapted to perform well on a different dataset. Traditional approaches often rely on simplifying assumptions about data distribution (like assuming Gaussian data), which limits their real-world applicability. The key issue is determining when and how a pretrained model can be effectively fine-tuned using limited data from a new distribution to achieve superior performance.
The researchers directly address this by focusing on linear models (simpler models that form the foundation for understanding more complex ones like deep neural networks). They develop a novel theoretical framework that provides exact and rigorous analysis of transfer learning performance, removing the need for typical Gaussian distribution assumptions. They introduce conditions under which fine-tuning improves the model. This research presents universal findings, meaning that the results apply across a broad range of data distributions beyond common assumptions, making them substantially more useful for practical applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a rigorous mathematical framework for understanding transfer learning in linear models. It moves beyond standard Gaussian assumptions, providing universal results applicable to a broader range of data distributions. This work is relevant to ongoing research on deep learning, offering insights into how pretrained models generalize and how to best fine-tune them for new tasks. The universality results are particularly impactful, greatly simplifying the analysis and broadening the applicability of the findings. It opens up new avenues of investigation into transfer learning in more complex models and scenarios.
Visual Insights#

🔼 The figure shows the generalization error of the weight obtained through running SGD with respect to k = 2 for the bilevel distribution. It compares the theoretical prediction (blue line) and lower bound (red line) with the empirical results from normal (black squares), Bernoulli (green circles), and chi-squared (red triangles) distributions. The plots are for different values of sigma (noise level).
read the caption
Figure 1: Generalization error for the bilevel distribution
In-depth insights#
Transfer Learning#
Transfer learning, a prominent machine learning paradigm, is explored in the context of linear models. The core idea is to leverage knowledge gained from a source domain with abundant data to improve model performance in a target domain where data is scarce. The research delves into the theoretical underpinnings of this approach, analyzing the generalization error of models when pretrained weights are fine-tuned using limited target data. A key finding is the establishment of universality theorems that show the model’s performance is determined by the first and second-order statistics of the target distribution, rather than its specific form. This result significantly broadens the applicability of transfer learning beyond commonly used Gaussian assumptions. The work also identifies precise conditions under which fine-tuning surpasses the performance of the pretrained model alone, providing valuable guidelines for practical applications of transfer learning within linear models.
Linear Model Analysis#
Linear model analysis within a machine learning context often involves simplifying complex systems to gain a better understanding of fundamental principles. This approach is particularly useful when studying transfer learning scenarios where a model, pre-trained on a source distribution, is fine-tuned on a target distribution. Overparametrized models, where the number of parameters exceeds the data points, are particularly amenable to linear model analysis due to their unique properties. This analysis is crucial for understanding the underlying mechanisms of transfer learning, and, more broadly, for providing rigorous explanations for the effectiveness of model-based transfer learning. The analysis can reveal insights into implicit regularization techniques employed during the fine-tuning process, often clarifying how specific optimizers guide the model’s generalization behavior. By focusing on linear models, researchers can derive closed-form solutions and conduct a precise error analysis in the asymptotic regime. The theoretical analysis will focus on generalization error in regression tasks and classification error in binary classification, revealing the conditions under which fine-tuning outperforms simply using a pre-trained model. In particular, the analysis will demonstrate that the performance of fine-tuned linear models is universal, meaning that the results extend beyond commonly made Gaussian assumptions to more general target data distributions. Understanding universality is key because it simplifies the analysis by enabling a shift to a Gaussian equivalent model that is more tractable. The results obtained from such linear model analyses often serve as foundational building blocks for subsequent analysis on more complex, deep learning models.
SGD Convergence#
The convergence of stochastic gradient descent (SGD) is a crucial aspect of training machine learning models, especially deep neural networks. Theoretical analysis of SGD convergence is challenging due to its stochastic nature and the non-convexity of loss functions. However, for linear models, under specific assumptions like sufficient overparameterization and appropriate regularization, strong convergence guarantees can often be derived. Such analysis often involves characterizing the trajectory of the iterates and proving that they approach a stationary point of the objective function or a specific solution depending on the underlying model and problem. The rate of convergence can also be investigated, providing insight into the efficiency of the algorithm. Factors such as step size, initialization, and data distribution significantly influence SGD’s convergence behavior. Understanding these factors is essential for effective model training and ensuring robust performance. Moreover, examining the generalization performance achieved after convergence allows researchers to analyze how well the learned model extrapolates to unseen data, thereby establishing a link between optimization and generalization.
Universality Theorem#
A Universality Theorem, in the context of machine learning, asserts that the performance of a model trained on one data distribution generalizes well to other distributions. This is particularly useful in transfer learning scenarios where labeled data is scarce. The theorem’s significance lies in its ability to provide theoretical guarantees for model performance across diverse datasets, reducing the reliance on extensive empirical validation. A key aspect often explored is the identification of sufficient conditions under which universality holds. This typically involves constraints on the data distributions or the model architecture, often focusing on the first and second-order statistics of the target data distribution, demonstrating that only these properties are crucial for generalization. The theorem’s robustness against deviations from specific distributional assumptions, such as Gaussianity, makes it highly impactful. A rigorous proof of such a theorem typically leverages sophisticated mathematical tools from probability theory and random matrix theory, to establish its validity. The Universality Theorem’s strength lies in its ability to provide a theoretical framework for understanding generalization in machine learning, especially in high-dimensional settings and scenarios with limited data.
Future Work#
The ‘Future Work’ section of this research paper could explore several promising avenues. Extending the universality results to non-convex loss functions or objectives with explicit regularization would significantly broaden the applicability of the findings. Investigating the impact of different optimization algorithms beyond SGD and analyzing the implications of universality in other machine learning contexts (e.g., deep learning) are also important directions. A rigorous analysis of the instance-based transfer learning approach, and comparing it to the model-based approach analyzed in this paper would offer valuable insights into the trade-offs between these two dominant methods. Finally, focusing on practical applications, especially in scenarios with limited data, and developing techniques to estimate the key statistical properties (first and second-order statistics) of the target distribution could greatly enhance the real-world applicability of the universality results.
More visual insights#
More on figures

🔼 This figure displays the generalization error for different input distributions (Normal, Bernoulli, Chi-squared) for three different noise levels (σ = 0.01, σ = 0.15, σ = 2). The x-axis represents the ratio of the number of parameters to samples (κ). The blue line shows the theoretical prediction from Theorem 2, while the red line represents a lower bound derived in the paper. The markers denote the actual empirical generalization error from simulations. The figure aims to illustrate the universality result of Theorem 1 for regression, showing how the generalization error is similar across different distributions.
read the caption
Figure 1: Generalization error for the bilevel distribution
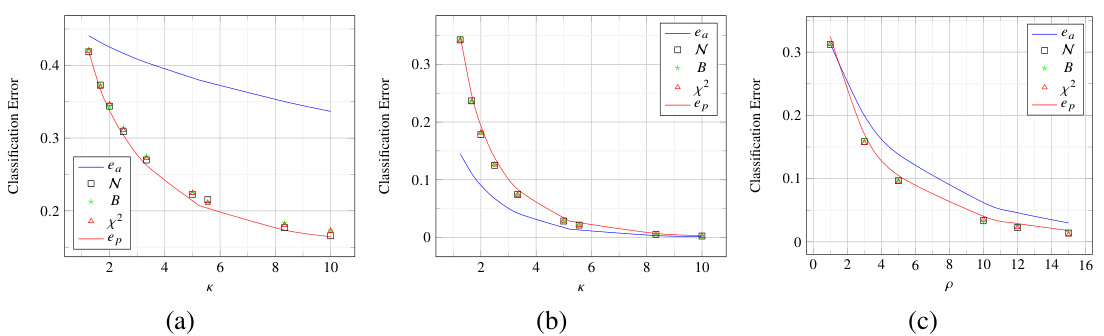
🔼 This figure shows the results of classification experiments using three different data distributions (Normal, Bernoulli, and Chi-squared) and varying the ratio of data points to parameters (κ). The plots compare the classification errors of pre-trained and fine-tuned models. Panel (a) fixes ρ=1 and varies κ. Panel (b) fixes κ=2 and varies ρ. Panel (c) shows how the classification error depends on p (ratio between dimensions of data and feature space) and different distributions. The figure demonstrates the universality property shown in the paper: similar results are obtained for various data distributions.
read the caption
Figure 3: Classification error
Full paper#



















