TL;DR#
Bi-level optimization (BLO) is essential for solving hierarchical machine learning problems, but traditional methods struggle with the scale and memory demands of modern deep learning models. This leads to inaccurate gradient estimations and limits the applicability of BLO in large-scale applications. Existing approaches either suffer from memory issues (gradient unrolling), approximation errors (implicit function methods), or both, hindering their performance in large-scale settings.
The paper introduces Forward Gradient Unrolling with Forward Gradient ((FG)²U), a novel algorithm to address these challenges. (FG)²U achieves an unbiased stochastic approximation of the meta-gradient, significantly improving gradient estimation accuracy. Its inherent support for parallel computing leads to substantial gains in computational efficiency. Extensive empirical evaluations across various large-scale tasks demonstrate (FG)²U’s superior performance compared to existing methods, showcasing its effectiveness in dealing with the memory and approximation challenges associated with large-scale BLO.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large-scale bi-level optimization problems. It offers a novel, memory-efficient solution, (FG)²U, which is highly relevant to current trends in deep learning and machine learning where models are increasingly complex and data-sets are massive. The superior performance demonstrated in diverse large-scale tasks opens up exciting avenues for future research in scalable bi-level optimization techniques and their applications in various domains.
Visual Insights#

🔼 This figure provides a comprehensive comparison of different bi-level optimization methods, highlighting the advantages of (FG)2U. The top left panel shows a comparison table, the top right panel illustrates a two-phase training paradigm, and the bottom panels show experimental results on Meta Learning Online Adaptation and Data Condensation tasks, demonstrating (FG)2U’s superior performance and efficiency. Specifically, it showcases how (FG)2U addresses the memory limitations of existing methods and achieves high accuracy in gradient approximations, even at large scales.
read the caption
Figure 1: Top Left: A comparison of bi-level optimization methods. (FG)2U circumvents the large-scale challenges inherent in classical bi-level optimization techniques. Within large-scale bi-level optimization, (FG)2U prioritizes the accuracy of gradient approximation over efficiency. Top Right: An overview of the cost-effective two-phase paradigm. (FG)2U is ideally positioned in Phase II to enhance performance after an approximate solution has been obtained using other efficient methods. Bottom Left: GPU Memory Usage and Performance on Meta Learning Online Adaptation experiment. (FG)2U can effectively address the memory issue of RGU when both the inner model and the unrolled depth are large. Bottom Center: GPU Memory Usage and Performance on Data Condensation experiments. The performance of (FG)2U surpasses that of other large-scale bi-level optimization methods, owing to its accurate gradient approximation, while demonstrating better memory efficiency. Bottom Right: Efficiency tradeoff of (FG)2U on Data Condensation experiments. The efficiency of (FG)2U can be well enhanced via intra/inter-GPU parallelism.
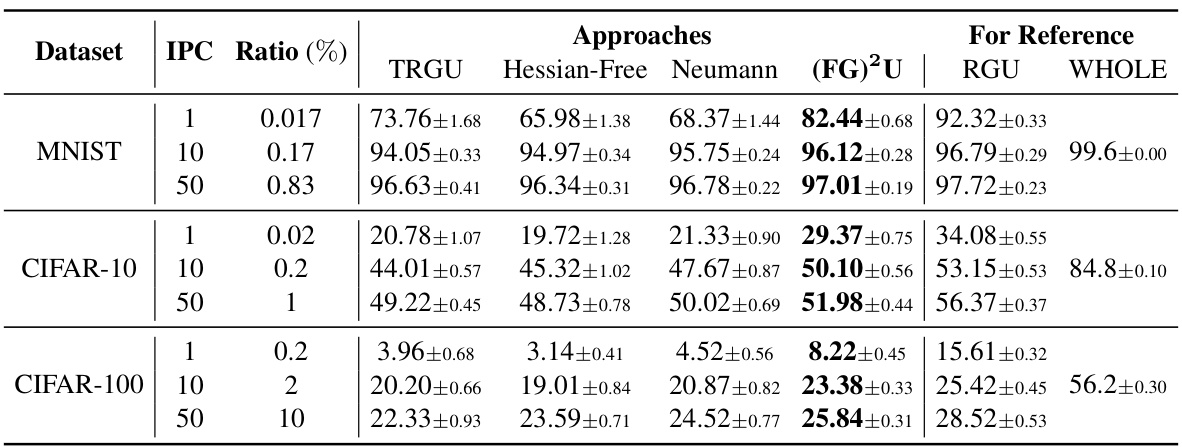
🔼 This table presents a comparison of the testing accuracy achieved by different bilevel optimization methods on three datasets (MNIST, CIFAR-10, and CIFAR-100) after performing data condensation. The table shows the results for various methods, including TRGU, Hessian-Free, Neumann, the proposed (FG)²U, RGU, and the results achieved using the whole datasets. Different image per class (IPC) ratios are considered. The table demonstrates the effectiveness of (FG)²U in achieving high accuracy, especially in large-scale scenarios, where other methods suffer from memory limitations or approximation errors.
read the caption
Table 1: The performance (testing accuracy %) comparison among various bilevel optimization methods on the data condensation task over three datasets. All the datasets are condensed using a 3-layer ConvNet. IPC: image(s) per class. Ratio (%): the ratio of condensed examples to the whole training set.
In-depth insights#
Bi-level Optimization#
Bi-level optimization (BLO) tackles hierarchical problems where one optimization task is nested within another. It’s crucial in machine learning for scenarios like hyperparameter optimization, where the outer level optimizes hyperparameters while the inner level trains the model using those parameters. BLO presents significant challenges due to its inherent complexity, particularly in large-scale applications. Traditional gradient-based approaches suffer from high memory consumption and biased gradient approximations. Recent advancements focus on developing memory-efficient and unbiased algorithms, often employing techniques like gradient unrolling or implicit differentiation to address the challenges. The trade-off between efficiency and accuracy remains a key area of focus, with a need to balance the computational cost against the precision of gradient approximations for practical applications in large-scale machine learning models. Developing algorithms capable of scaling efficiently to handle increasingly complex models is paramount.
FG²U Algorithm#
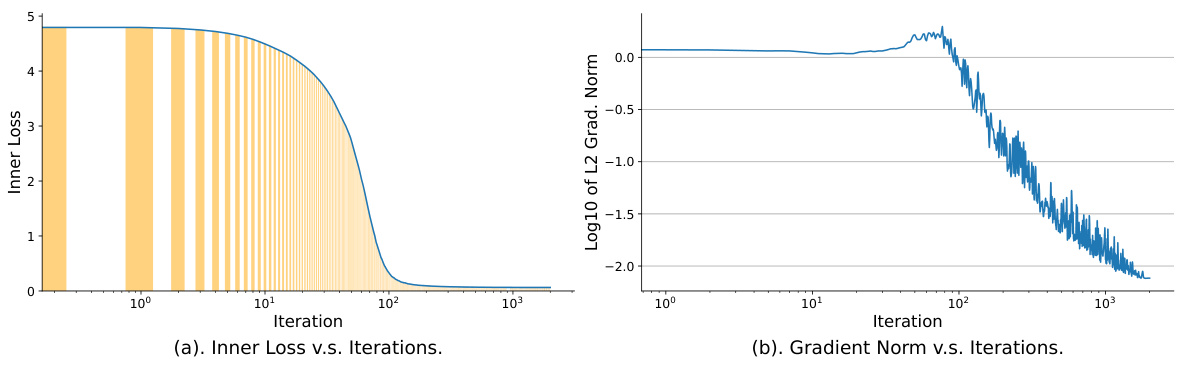
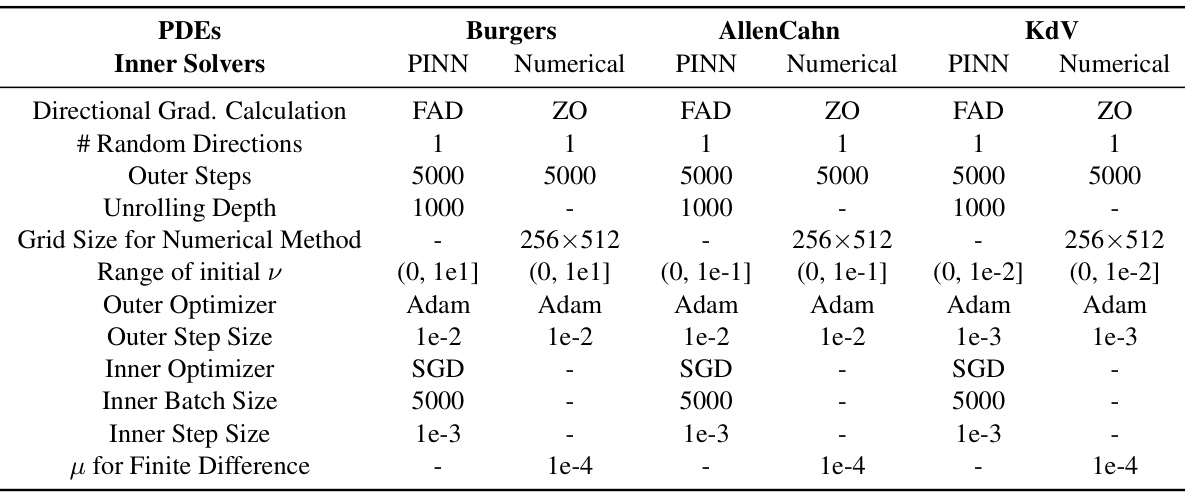
The FG²U (Forward Gradient Unrolling with Forward Gradient) algorithm presents a novel approach to large-scale bi-level optimization. It cleverly addresses the limitations of existing methods like gradient unrolling (high memory cost) and implicit function approaches (approximation errors). FG²U achieves an unbiased stochastic approximation of the meta-gradient, circumventing memory issues by tracking a low-dimensional vector rather than the full Jacobian matrix. This efficiency gain is further enhanced by its inherent suitability for parallel computation. A key strength lies in its ability to provide significantly more accurate gradient estimates than traditional methods, ultimately leading to superior performance in large-scale applications. The algorithm’s effectiveness is demonstrated through its application to various tasks, showcasing its adaptability and robustness across diverse problem settings. The two-phase paradigm proposed, involving a combination of FG²U with other more efficient but less accurate methods, enhances overall cost-effectiveness. Despite the convergence analysis demonstrating a dimension-dependent convergence rate, the algorithm proves practical via considerations like careful sample size selection and leveraging parallel computing resources.
Memory Efficiency#
The research emphasizes memory efficiency as a critical factor in large-scale bi-level optimization. Traditional gradient-based methods often struggle with memory constraints due to the storage of intermediate gradients or Hessian matrices. The proposed method, (FG)²U, directly addresses this by using forward gradient unrolling with forward gradient calculations. This approach avoids the need to store the full trajectory of inner optimization steps, significantly reducing the memory footprint. The unbiased stochastic gradient estimation further enhances efficiency. Unlike other approaches that trade accuracy for efficiency by introducing approximation biases, (FG)²U prioritizes accurate gradient estimation, leading to improved performance despite its inherent computational demands. The inherent parallelizability of the algorithm further enhances its efficiency on large-scale computing systems, enabling cost-effective two-phase paradigms where less computationally-expensive methods could be used in the initial stage before applying (FG)²U for more accurate optimization.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and effectiveness of any optimization algorithm. In the context of a research paper, a section dedicated to convergence analysis would delve into the theoretical guarantees of the proposed method. This typically involves defining assumptions about the problem’s structure (e.g., convexity, smoothness of objective functions), and then proving that the algorithm’s iterates converge to a solution under these assumptions. Key aspects often include establishing convergence rates, demonstrating the algorithm’s stability (i.e., its robustness to noise or perturbations), and potentially providing bounds on the error of the approximation. The mathematical techniques employed could range from elementary calculus and linear algebra to more advanced tools from optimization theory, such as Lyapunov functions or contraction mappings. A well-conducted convergence analysis not only assures theoretical soundness but also provides valuable insights into the algorithm’s behavior, suggesting areas for improvement or identifying potential limitations. The types of convergence demonstrated might include convergence in probability, almost sure convergence, or convergence in expectation. Furthermore, a strong convergence analysis builds confidence in the practical efficacy of the algorithm, making it a cornerstone of many research papers focusing on novel optimization strategies.
Future Work#
Future research directions stemming from this work could center on enhancing the scalability of the proposed (FG)“2U algorithm. Addressing the inherent computational costs associated with large-scale bi-level optimization is crucial. This could involve exploring more efficient gradient approximation techniques, potentially leveraging advanced hardware or distributed computing strategies. A significant area for future investigation is the application of (FG)“2U to a wider range of challenging problems, including those characterized by black-box optimization scenarios, where the inner problem is computationally complex or difficult to model directly. Furthermore, a thorough investigation into the algorithm’s robustness and sensitivity to hyperparameter choices would provide valuable insights. Finally, expanding the theoretical analysis to encompass a broader set of assumptions and optimization problem types would contribute to a more comprehensive understanding of (FG)“2U’s capabilities and limitations.
More visual insights#
More on figures
🔼 This figure compares (FG)²U to other bi-level optimization methods, highlighting its ability to handle large-scale problems by prioritizing accuracy over efficiency. It also illustrates a two-phase training paradigm where (FG)²U is used in the second phase for refinement after an initial approximation. Experiments on meta-learning and data condensation demonstrate (FG)²U’s superior memory efficiency and performance, especially when leveraging parallel computing.
read the caption
Figure 1: Top Left: A comparison of bi-level optimization methods. (FG)²U circumvents the large-scale challenges inherent in classical bi-level optimization techniques. Within large-scale bi-level optimization, (FG)²U prioritizes the accuracy of gradient approximation over efficiency. Top Right: An overview of the cost-effective two-phase paradigm. (FG)²U is ideally positioned in Phase II to enhance performance after an approximate solution has been obtained using other efficient methods. Bottom Left: GPU Memory Usage and Performance on Meta Learning Online Adaptation experiment. (FG)²U can effectively address the memory issue of RGU when both the inner model and the unrolled depth are large. Bottom Center: GPU Memory Usage and Performance on Data Condensation experiments. The performance of (FG)²U surpasses that of other large-scale bi-level optimization methods, owing to its accurate gradient approximation, while demonstrating better memory efficiency. Bottom Right: Efficiency tradeoff of (FG)²U on Data Condensation experiments. The efficiency of (FG)²U can be well enhanced via intra/inter-GPU parallelism.
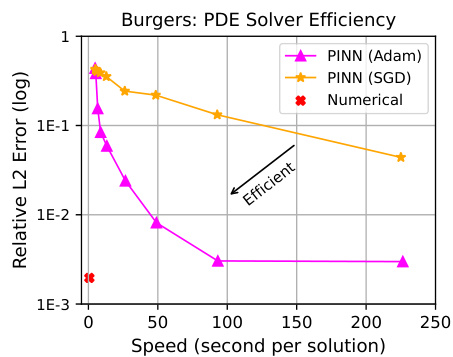
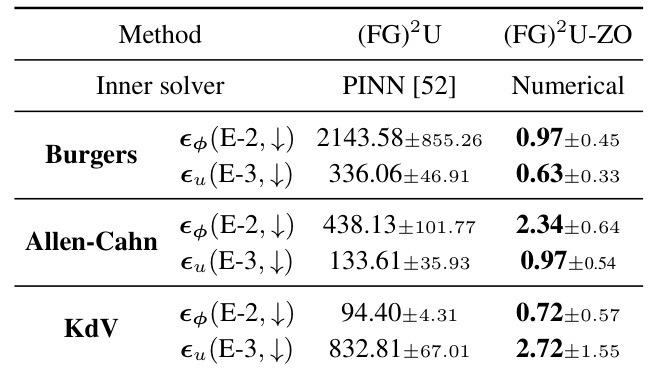
🔼 This figure compares the efficiency and accuracy of Physics-Informed Neural Networks (PINNs) and numerical solvers for solving partial differential equations (PDEs). The left panel shows that numerical solvers are significantly more efficient than PINNs, especially as the number of optimization steps increases. The right panel shows that (FG)2U, using numerical solvers, achieves significantly lower relative L2 errors in predicting both the PDE parameters (φ) and the solution (u) compared to PINNs.
read the caption
Figure 2: Left: Comparison of efficiency between the PINN solver and the numerical solver. We evaluated Adam [29] and SGD as the inner optimizers for the PINN solver, with steps ranging from 100 to 50,000. The results demonstrate that the numerical solver is significantly more efficient. Right: Comparison of relative L2 errors in the prediction of φ and u. εφ = ||φpred - φ||2/||φ||2, εu = ||upred - u||2/||u||2.
🔼 This figure summarizes the contributions of the paper. It presents a comparison of (FG)²U with other bi-level optimization methods, highlighting its ability to overcome memory limitations and achieve accurate gradient approximations, even in large-scale settings. It also shows the cost-effective two-phase training paradigm suggested by the authors. Empirical evaluations illustrate (FG)²U’s performance on meta-learning and data condensation tasks and its memory and efficiency trade-offs.
read the caption
Figure 1: Top Left: A comparison of bi-level optimization methods. (FG)²U circumvents the large-scale challenges inherent in classical bi-level optimization techniques. Within large-scale bi-level optimization, (FG)²U prioritizes the accuracy of gradient approximation over efficiency. Top Right: An overview of the cost-effective two-phase paradigm. (FG)²U is ideally positioned in Phase II to enhance performance after an approximate solution has been obtained using other efficient methods. Bottom Left: GPU Memory Usage and Performance on Meta Learning Online Adaptation experiment. (FG)²U can effectively address the memory issue of RGU when both the inner model and the unrolled depth are large. Bottom Center: GPU Memory Usage and Performance on Data Condensation experiments. (FG)²U can effectively address the memory issue of RGU when both the inner model and the unrolled depth are large. Bottom Right: Efficiency tradeoff of (FG)²U on Data Condensation experiments. The efficiency of (FG)²U can be well enhanced via intra/inter-GPU parallelism.

🔼 This figure provides a comprehensive comparison of different bi-level optimization methods, highlighting the advantages of the proposed (FG)2U approach. It showcases (FG)2U’s ability to overcome memory limitations and achieve higher accuracy in gradient approximation compared to existing techniques. The figure also illustrates a two-phase training paradigm where (FG)2U is used in the second phase for improved accuracy after an initial approximation. Results from Meta Learning and Data Condensation experiments demonstrate (FG)2U’s superior performance and efficiency, especially when leveraging parallel GPU computation.
read the caption
Figure 1: Top Left: A comparison of bi-level optimization methods. (FG)2U circumvents the large-scale challenges inherent in classical bi-level optimization techniques. Within large-scale bi-level optimization, (FG)2U prioritizes the accuracy of gradient approximation over efficiency. Top Right: An overview of the cost-effective two-phase paradigm. (FG)2U is ideally positioned in Phase II to enhance performance after an approximate solution has been obtained using other efficient methods. Bottom Left: GPU Memory Usage and Performance on Meta Learning Online Adaptation experiment. (FG)2U can effectively address the memory issue of RGU when both the inner model and the unrolled depth are large. Bottom Center: GPU Memory Usage and Performance on Data Condensation experiments. The performance of (FG)2U surpasses that of other large-scale bi-level optimization methods, owing to its accurate gradient approximation, while demonstrating better memory efficiency. Bottom Right: Efficiency tradeoff of (FG)2U on Data Condensation experiments. The efficiency of (FG)2U can be well enhanced via intra/inter-GPU parallelism.
More on tables

🔼 This table compares the performance of three different methods for online adaptation of language models: CaMeLS + RGU (results from the original paper), CaMeLS + RGU (our implementation), and CaMeLS + (FG)²U (our proposed method). The comparison is done across three different language models (DistilGPT2, GPT2-Large, and GPT2-XL) and two datasets (StreamingQA and SQUAD-Seq). The evaluation metrics used are Exact Match (EM) and F1 score. The table highlights that our method, (FG)²U, consistently achieves better results than the other two.
read the caption
Table 2: Comparison of the online adaptation performance. The reported evaluation metrics include the exact match (EM) and F1 scores. For vanilla CaMeLS [25], RGU is conducted with unrolled depth 6, using DistilGPT2 as the base model. We present both the results reported by [66] and those from our implementation (denoted as impl.). For CaMeLS + (FG)²U, we select unrolled depths from {24, 48}, and the base model from {DistilGPT2, GPT2}. We report the results for the combination that yields the best F1 score. Additional details and ablation studies are documented in Appendix G.1.
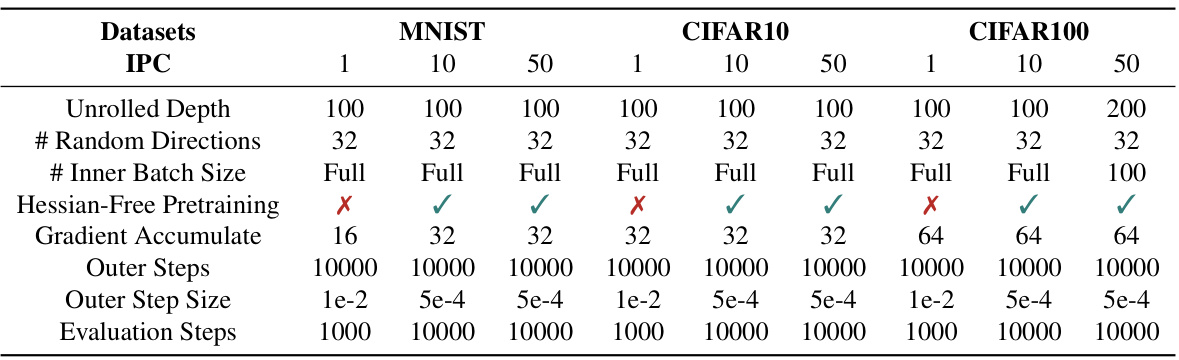
🔼 This table compares the performance of various bilevel optimization methods on three different datasets (MNIST, CIFAR-10, and CIFAR-100) for a data condensation task. The performance is measured by testing accuracy. Different image per class (IPC) ratios and overall dataset ratios are tested. The table shows that (FG)²U outperforms other methods.
read the caption
Table 1: The performance (testing accuracy %) comparison among various bilevel optimization methods on the data condensation task over three datasets. All the datasets are condensed using a 3-layer ConvNet. IPC: image(s) per class. Ratio (%): the ratio of condensed examples to the whole training set.

🔼 This table compares the performance of different methods for online adaptation of language models. It shows the exact match (EM) and F1 scores for the CaMeLS approach using RGU (with DistilGPT2) and the proposed (FG)²U method (with DistilGPT2 and GPT2 models) on two datasets. Different unrolled depths are tested for (FG)²U, demonstrating its ability to handle larger models and depths.
read the caption
Table 2: Comparison of the online adaptation performance. The reported evaluation metrics include the exact match (EM) and F1 scores. For vanilla CaMeLS [25], RGU is conducted with unrolled depth 6, using DistilGPT2 as the base model. We present both the results reported by [66] and those from our implementation (denoted as impl.). For CaMeLS + (FG)²U, we select unrolled depths from {24, 48}, and the base model from {DistilGPT2, GPT2}. We report the results for the combination that yields the best F1 score. Additional details and ablation studies are documented in Appendix G.1.
🔼 This table compares the performance of different bilevel optimization methods on three image datasets (MNIST, CIFAR-10, CIFAR-100) using a data condensation technique. The performance is measured by testing accuracy, and it’s shown for different image per class (IPC) ratios, which represent the proportion of condensed examples to the total number of examples in the training dataset. The results are compared to using the whole dataset for training (WHOLE).
read the caption
Table 1: The performance (testing accuracy %) comparison among various bilevel optimization methods on the data condensation task over three datasets. All the datasets are condensed using a 3-layer ConvNet. IPC: image(s) per class. Ratio (%): the ratio of condensed examples to the whole training set.
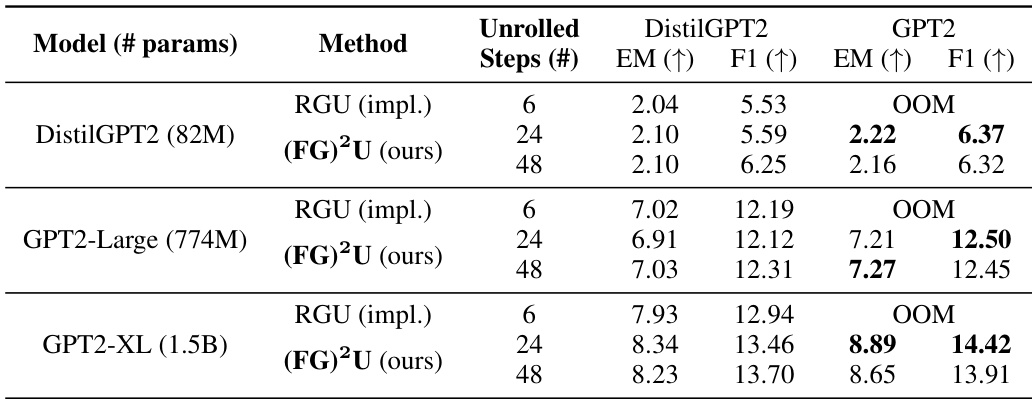
🔼 This table compares the performance of the CaMeLS model using RGU and (FG)²U for online adaptation of language models on two datasets, StreamingQA and SQUAD-Seq. It shows the Exact Match (EM) and F1 scores for different model sizes and unrolled depths. The results demonstrate that (FG)²U achieves better performance than RGU, especially for larger models, overcoming the memory limitations of RGU.
read the caption
Table 2: Comparison of the online adaptation performance. The reported evaluation metrics include the exact match (EM) and F1 scores. For vanilla CaMeLS [25], RGU is conducted with unrolled depth 6, using DistilGPT2 as the base model. We present both the results reported by [66] and those from our implementation (denoted as impl.). For CaMeLS + (FG)²U, we select unrolled depths from {24, 48}, and the base model from {DistilGPT2, GPT2}. We report the results for the combination that yields the best F1 score. Additional details and ablation studies are documented in Appendix G.1.
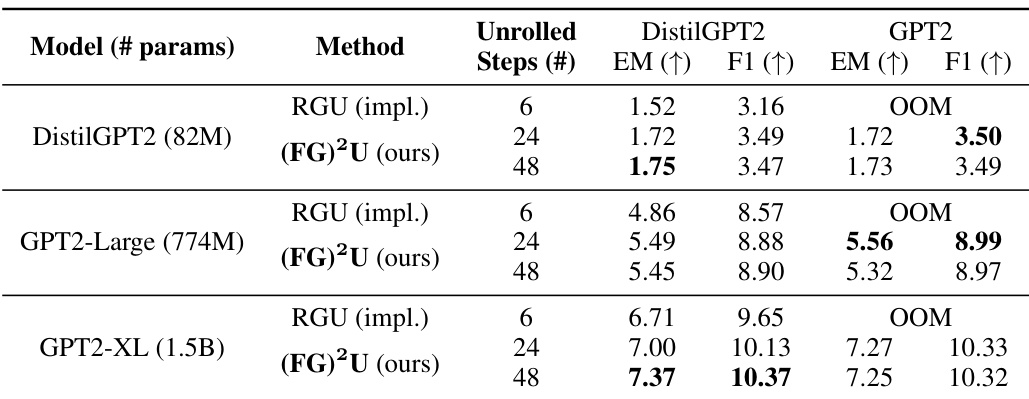
🔼 This table compares the performance of different methods for online adaptation of language models on two datasets: StreamingQA and SQUAD-Seq. It shows the exact match (EM) and F1 scores for CaMeLS with RGU (results from the original paper and the authors’ implementation) and CaMeLS with (FG)²U. The table highlights (FG)²U’s improved performance, especially when using larger language models and increased unrolled depth, overcoming the memory limitations of RGU.
read the caption
Table 2: Comparison of the online adaptation performance. The reported evaluation metrics include the exact match (EM) and F1 scores. For vanilla CaMeLS [25], RGU is conducted with unrolled depth 6, using DistilGPT2 as the base model. We present both the results reported by [66] and those from our implementation (denoted as impl.). For CaMeLS + (FG)²U, we select unrolled depths from {24, 48}, and the base model from {DistilGPT2, GPT2}. We report the results for the combination that yields the best F1 score. Additional details and ablation studies are documented in Appendix G.1.
Full paper#