A Single-Step, Sharpness-Aware Minimization is All You Need to Achieve Efficient and Accurate Sparse Training

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning and optimization because it directly tackles the challenge of efficient and accurate sparse training, a critical issue in scaling deep neural networks. The proposed S2-SAM method offers a significant improvement in accuracy across various sparse training methods without increasing computational cost, addressing a major bottleneck in the field. It also provides theoretical analysis, furthering our understanding of sparse training and opening new avenues for exploring efficient training strategies in large-scale models.

Visual Insights

#

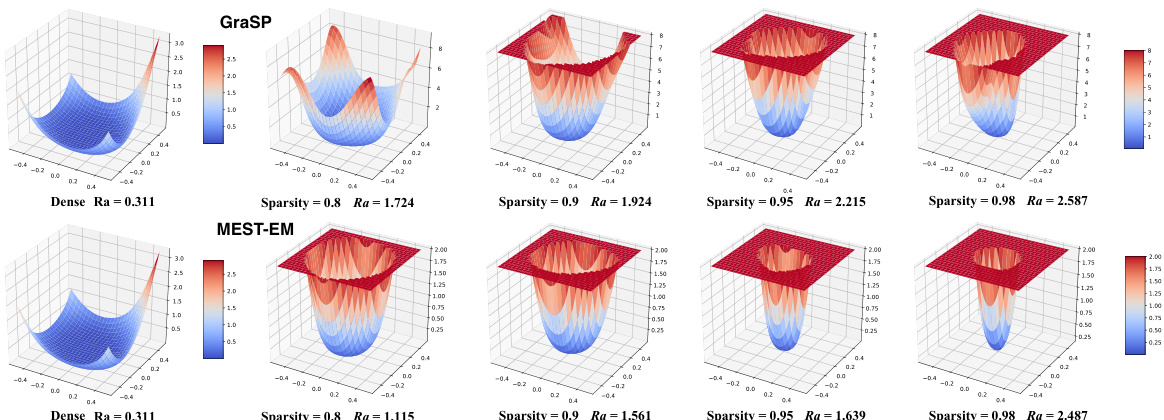
🔼 This figure visualizes the loss surface behavior for training sparse neural networks using ResNet-32 on CIFAR-10. Two different sparse training methods (GraSP and MEST-EM) are shown, each with varying levels of sparsity (0.8, 0.9, 0.95, 0.98). The sharpness of the loss surface is quantified using the coefficient Ra. The visualization demonstrates that as sparsity increases, the loss surface becomes sharper and steeper, indicating a more challenging optimization problem.

read the caption

Figure 1: The loss surface visualization for training a sparse neural network using ResNet-32 on CIFAR-10. We select two representative sparse training methods [18, 3] and incorporate different levels of sparsity. We also quantify the loss surface behavior using coefficient Ra [19] to evaluate sharpness. With increased sparsity, Ra becomes larger, indicating sharper and steeper surface.

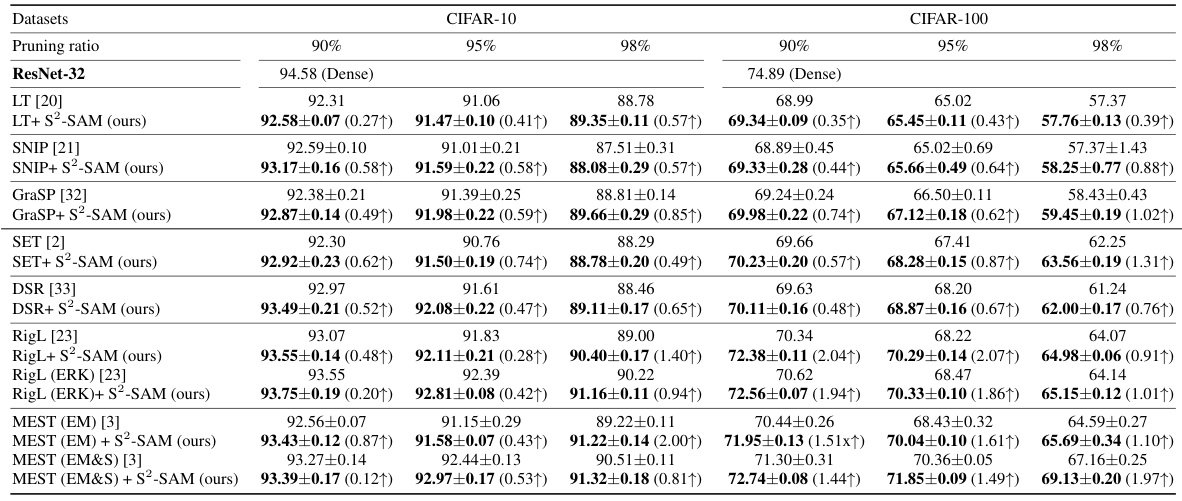
🔼 This table presents the test accuracy results for pruned ResNet-32 on CIFAR-10 and CIFAR-100 datasets. It compares the performance of various sparse training methods (LT, SNIP, GraSP, SET, DSR, RigL, MEST) with and without the proposed S2-SAM method. Different pruning ratios (90%, 95%, 98%) are tested for each method. The numbers in parentheses indicate the accuracy improvement achieved by adding S2-SAM.

read the caption

Table 1: Test accuracy (%) of pruned ResNet-32 on CIFAR-10/100.

In-depth insights

#

Sparse Training

#

Sparse training tackles the challenge of training large deep neural networks (DNNs) by reducing computational cost and memory usage. This is achieved by reducing the number of parameters in the network, resulting in a sparse model. The core idea is that many parameters in DNNs are redundant or have minimal impact on the model’s performance, so removing them does not significantly hurt accuracy. However, training sparse models presents its own set of challenges. Finding the optimal sparsity level that balances accuracy and efficiency is crucial. Maintaining good generalization ability remains difficult, as the reduced number of parameters can limit the model’s expressiveness. The paper explores the relationship between sparsity and the complexity of the loss landscape and introduces a new technique, seeking to mitigate these challenges. The use of gradient information to approximate perturbation is a key innovation, which reduces the computational cost of achieving sharpness-aware minimization. The method aims to find flatter minima, which is important for improving model generalization.

S2-SAM Algorithm

#

The hypothetical ‘S2-SAM Algorithm’ presented in the research paper appears to be a novel single-step approach to Sharpness-Aware Minimization (SAM), specifically tailored for sparse neural network training. Its key innovation lies in approximating the sharpness perturbation using prior gradient information, eliminating the need for a second gradient calculation as in traditional SAM. This significantly improves efficiency, aligning with the core goal of sparse training which aims to reduce computational cost. The algorithm’s effectiveness is likely attributed to its ability to identify flatter minima on the often chaotic loss landscapes of sparse networks, thereby improving generalization performance. Zero extra computational cost is a major advantage, making it a readily deployable and practical improvement for existing sparse training methods. The theoretical proof for convergence further supports the algorithm’s robustness and reliability. The experimental results demonstrate its broad applicability and effectiveness across various sparse training techniques, consistently enhancing accuracy and showing particular efficacy with high sparsity levels. However, further investigation is warranted to explore the algorithm’s performance with different network architectures, datasets, and hyperparameter settings. The impact of the single-step approximation on convergence speed and the stability across a wider range of problems also requires deeper analysis.

Generalization Analysis

#

A robust generalization analysis is crucial for evaluating the effectiveness of any machine learning model, especially in the context of sparse neural networks. This section would ideally delve into the theoretical guarantees of the proposed method, focusing on how it addresses the challenges associated with training sparse models. Key aspects would include: bounding the generalization error, analyzing the convergence properties of the algorithm, and potentially providing theoretical justification for why the single-step sharpness-aware approach improves generalization over traditional methods. The analysis should incorporate relevant theoretical frameworks, such as PAC-Bayesian bounds or stability analysis, to support the claims made. Empirical validation of these theoretical findings through experiments, comparing generalization performance across different sparse training methods and sparsity levels would further strengthen the analysis. Addressing the impact of sparsity on the loss landscape and its effect on generalization is another important aspect. A thorough analysis may also explore the relationship between sharpness, flat minima, and generalization, providing insights into why the single-step approach effectively finds flatter minima. Finally, the section should clearly discuss any limitations of the theoretical analysis and potential avenues for future work.

Experimental Results

#

The section on Experimental Results would ideally present a comprehensive evaluation of the proposed S2-SAM method. This should involve a robust comparison against existing state-of-the-art sparse training techniques across a diverse range of datasets and network architectures. Key aspects to include are: quantitative metrics such as accuracy, precision, recall, and F1-score; visualization of results, such as graphs showing accuracy improvements over training epochs; analysis of computational efficiency gains achieved by S2-SAM compared to other methods; and a discussion of any observed trade-offs between accuracy and efficiency. The results should clearly demonstrate the effectiveness of the single-step sharpness-aware minimization approach in enhancing both accuracy and efficiency of sparse training, specifically highlighting any situations where S2-SAM shows significant advantages. A strong analysis should also address the robustness of the method, potentially including experiments that assess the performance under various levels of sparsity, noise, or other challenging conditions. It is vital to carefully interpret and present the statistical significance of the reported results, employing appropriate measures such as confidence intervals to avoid overstating the impact of the findings. Finally, the presentation should be clear, well-organized, and effectively communicate the key findings and their implications.

Future Research

#

The paper’s conclusion mentions leaving the exploration of S²-SAM’s application to dense model training for future research. This is a significant direction, as the core idea of single-step sharpness-aware minimization could potentially benefit a wider array of models beyond sparse networks. Future work should investigate the effectiveness and efficiency of S²-SAM on densely-connected models, comparing its performance against traditional SAM and other optimization methods. A theoretical analysis comparing the convergence rates and generalization properties of S²-SAM in dense vs. sparse settings would be valuable. Additionally, the study could explore the interplay between S²-SAM and different regularization techniques or architectural choices in dense networks. Extending the theoretical analysis to address non-convex loss functions is also crucial for a wider applicability. Finally, a comparative analysis showing S²-SAM’s performance across diverse datasets and network architectures in dense model training would further solidify its place as a robust optimization technique.

More visual insights

#

More on figures

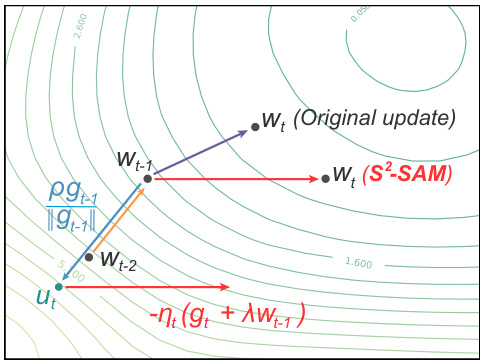
🔼 This figure illustrates how S²-SAM approximates the sharpness perturbation using the gradient from the previous step. In traditional SAM, two gradient computations are needed: one at the current weights and another at the weights perturbed by the sharpness. S²-SAM simplifies this by approximating the perturbed gradient using only the gradient from the previous step, resulting in zero extra computational cost. The figure shows the weight update path for both the original SAM method and the proposed S²-SAM method, highlighting how S²-SAM efficiently achieves a similar effect. This approximation is based on the intuition that the gradient direction from the previous step represents a direction of relatively high sharpness.

read the caption

Figure 2: Illustration of the optimization mechanism of S²-SAM. The perturbation on the current weights is approximated by the weight gradients from prior step. Please see Section 2.2 for detailed discussion.

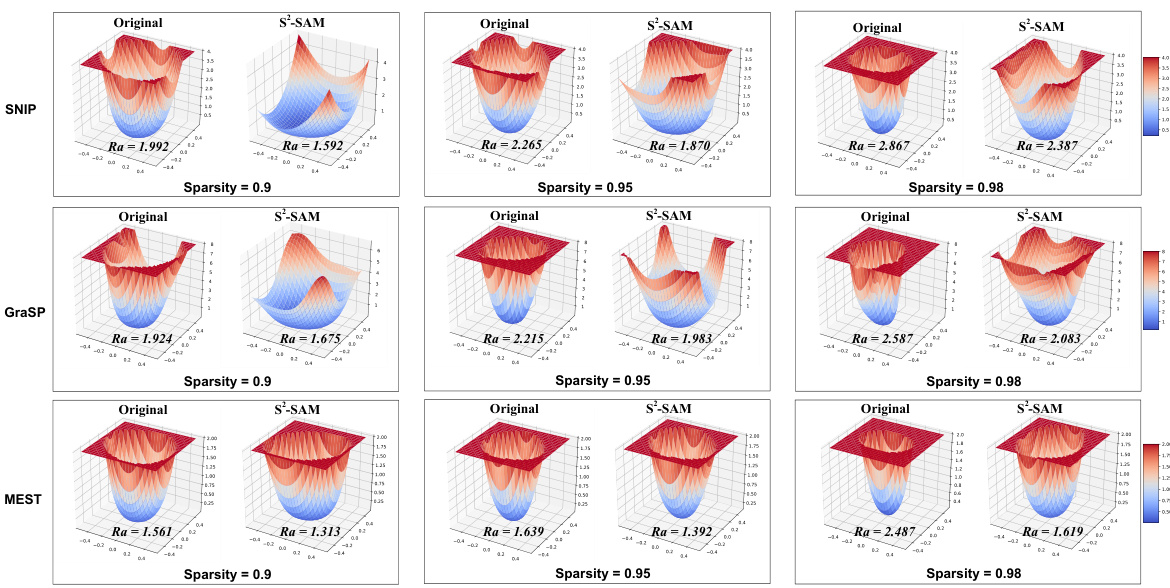
🔼 This figure visualizes the loss surface of three different sparse training methods (SNIP, GraSP, and MEST) at various sparsity levels (0.9, 0.95, and 0.98). For each method and sparsity level, two 3D plots are shown: one for the original training and one for training with the proposed S2-SAM method. The plots illustrate the shape of the loss landscape, with the color intensity representing the loss value. A key observation is that S2-SAM consistently leads to a wider and smoother loss surface (indicated by the lower Ra values), which is associated with better generalization performance. The Ra coefficient quantifies the sharpness of the loss surface; a lower Ra value indicates a flatter and less chaotic landscape.

read the caption

Figure 3: Loss surface sharpness comparison of different sparse training methods with original training and with S2-SAM. We also quantitatively evaluate the coefficient Ra. Using S2-SAM compared to the original method results in a smaller Ra, indicating a wider and smoother loss surface, which suggests improved generalization ability.

More on tables

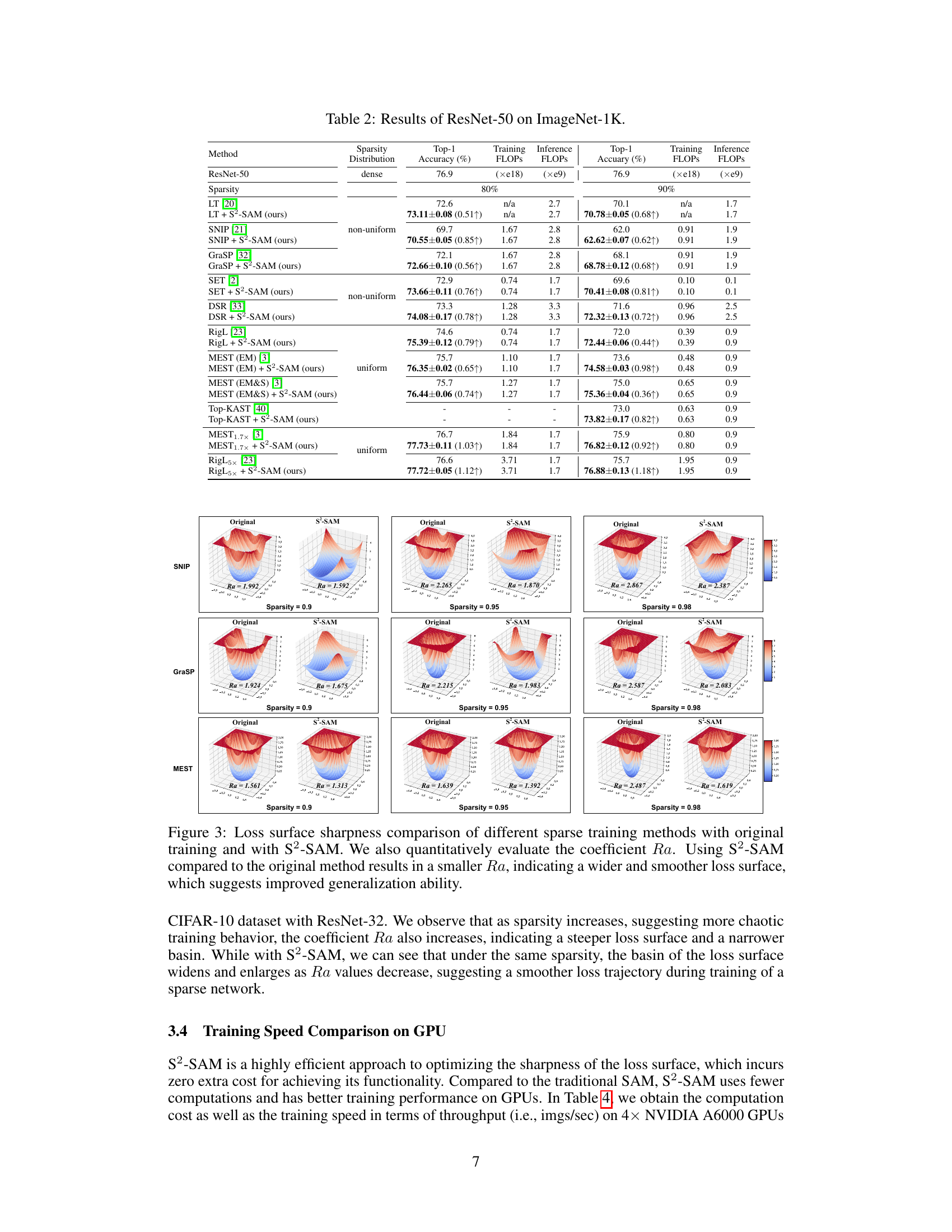
🔼 This table presents the results of applying different sparse training methods and S2-SAM to ResNet-50 on the ImageNet-1K dataset. For each method, it shows the sparsity level (80% and 90%), the sparsity distribution (uniform or non-uniform), the top-1 accuracy, and the training and inference FLOPs (floating-point operations). The table highlights the improvement in top-1 accuracy achieved by using S2-SAM in conjunction with various sparse training methods. It also demonstrates the effect of S2-SAM on different sparsity levels and sparsity patterns.

read the caption

Table 2: Results of ResNet-50 on ImageNet-1K.

🔼 This table presents the results of applying the proposed S2-SAM method to structured sparse training methods, specifically CHEX and Chase, on ResNet-34 and ResNet-50 networks. It compares the accuracy achieved with original training methods versus those employing S2-SAM, illustrating the performance gains obtained by incorporating S2-SAM. FLOPs (floating point operations) are also provided to show the computational cost.

read the caption

Table 3: Accuracy of S2-SAM on structured sparse training CHEX [10] and Chase [39].

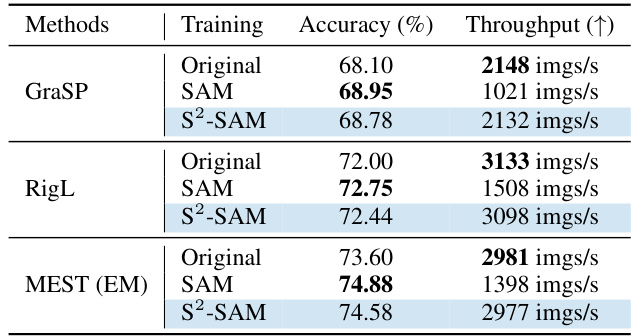
🔼 This table compares the training speed (throughput) of three different sparse training methods (GraSP, RigL, and MEST (EM)) with and without the proposed S2-SAM and the original SAM method. The throughput is measured in images per second (imgs/s) and shows the impact of each optimization technique on the training speed. The results suggest that S2-SAM maintains a comparable training speed to the original methods while SAM shows significantly lower throughput.

read the caption

Table 4: Training speed of SAM [25] and S2-SAM for different sparse training at 90% sparsity.

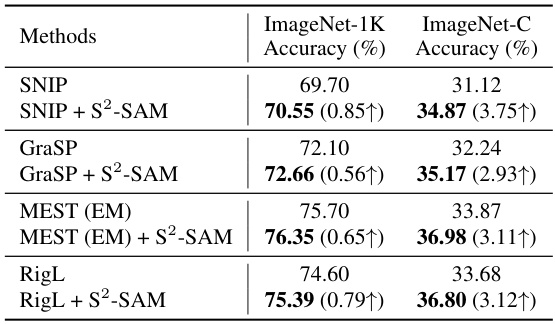
🔼 This table presents the ImageNet-C test accuracy results for different sparse training methods, both with and without the application of the proposed S2-SAM method. It highlights the improvement in robustness against image corruptions that S2-SAM provides. The 80% sparsity level is consistent across all models. The improvement in accuracy (shown in parentheses) is particularly noteworthy for the challenging ImageNet-C dataset, demonstrating S2-SAM’s effectiveness in enhancing model generalization and robustness.

read the caption

Table 5: Testing accuracy on ImageNet-C test set. We compare the results with and without S2-SAM using 80% sparsity.

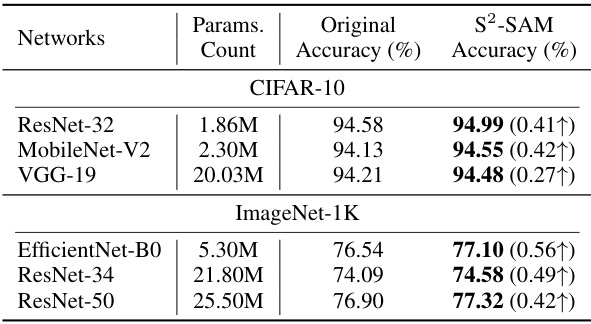
🔼 This table presents the test accuracy results for pruned ResNet-32 on CIFAR-10 and CIFAR-100 datasets. It compares the performance of several state-of-the-art sparse training methods (LT, SNIP, GraSP, SET, DSR, RigL, and MEST) with and without the proposed S2-SAM method. The results are shown for different pruning ratios (90%, 95%, and 98%). The improvement achieved by adding S2-SAM to each baseline method is also indicated.

read the caption

Table 1: Test accuracy (%) of pruned ResNet-32 on CIFAR-10/100.

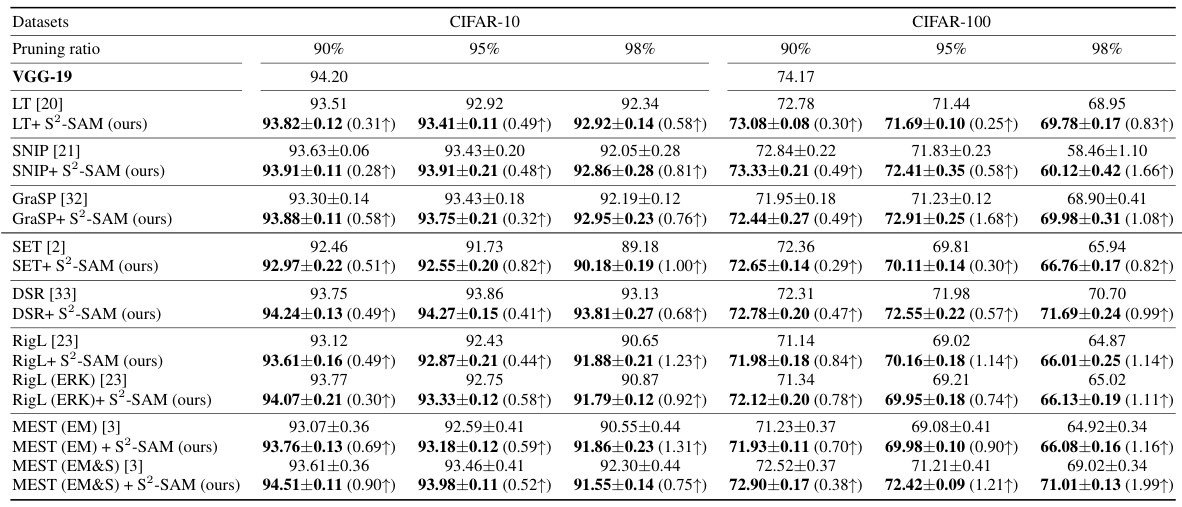
🔼 This table presents the test accuracy results achieved by various sparse training methods when applied to the VGG-19 model on CIFAR-10 and CIFAR-100 datasets. Different pruning ratios (90%, 95%, and 98%) are considered. The results are compared with and without the application of the proposed S2-SAM method, highlighting the accuracy improvements obtained. The table showcases the impact of S2-SAM across multiple existing sparse training techniques, both static and dynamic.

read the caption

Table A.1: Test accuracy (%) of pruned VGG-19 on CIFAR-10/100.

Full paper

#